仿生硅藻结构圆周位置和间距对轴承润滑性能的影响*

胡 宇 王优强 左名玉 房玉鑫 莫 君

(1.青岛理工大学机械与汽车工程学院 山东青岛 266520；2.工业流体节能与污染控制教育部重点实验室 山东青岛 266520)

随着工业技术的迅猛发展，人们对机械设备的降低摩擦磨损，减少能耗的要求越来越高。表面织构因其能够有效提高承载力，减小摩擦副表面的摩擦和磨损等特点，被广泛地应用于机械摩擦领域。

国内外很多研究学者已经对织构化表面的摩擦学特性开展研究,但现阶段大部分的织构研究主要是以单层织构为主，这是因为单层织构易于加工，润滑摩擦效果较好等特点。其中常见的织构形状多为圆形、椭圆形、正方形、菱形、三角形。但由于这类单层织构仅能发生一次动压效应，在润滑摩擦方面的性能仍不够突出。

随着仿生机械学的快速发展，很多学者基于某些生物[1-2]的表面形状，如鲨鱼[3-4]、猪笼草的表面[5-9]及牛的膝关节[10]等生物组织结构，进行织构仿真设计研究，获得了优异的减摩效果。硅藻的细胞壁具有精致的多级孔状结构，该结构有极高的抗拉性能和弹性韧性，具有良好的机械性能优势，国内外很多学者已经对硅藻结构进行了研究。2002年，SUMPER[11]通过实验观察了圆筛藻的结构；KRÖGER[12]通过电子扫描显微镜观察了硅藻的细胞结构。HAMM等[13]通过实验和仿真的方法研究发现，硅壳结构具有较强的自防御功能；文献[14]通过观察典型硅藻结构，发现其形状不同所产生的摩擦性能也存在差异；LOSIC等[15]通过探究圆筛藻生物表面结构和机械性能，发现圆筛藻硅壳因其孔层不同产生不同的硬度和弹性模量。尽管我国对于硅藻的研究起步较晚，但仍取得了较为丰硕的成果。李琛[16]通过实验制备圆筛藻硅质壳三维纳米材料并进行了结构表征。文献[17-20]基于硅藻结构设计了一种复合型织构并分析该织构在水润滑轴承表面的摩擦学特性。桂超[21]通过数值仿真分析了考虑轴承气穴和热效应影响下的织构轴承的摩擦学性能。陈林[22]通过仿真分析，研究了热作用下复合织构轴承的摩擦学性能和噪声水平变化。但这些研究没有分析过复合型织构在轴承不同位置和间距变化的影响。

本文作者基于硅藻的多级孔结构，在水润滑轴承表面设计矩形-半球型复合型织构，采用流固耦合研究复合型织构在水润滑轴承中高压区不同位置和间距的摩擦学特性。

1 分析模型

1.1 表面织构几何模型

由于流固耦合计算复杂且运算时间较长，为了方便研究计算,研究对象选择轴承的一个具有表面织构的单元进行分析。

如图1所示为水润滑轴承在高压区上具有织构的单元模型。

图1 在水润滑轴承高压区上的织构的单元模型

如图1(a)所示，轴承外径为200 mm，内径为100.2 mm，半径间隙为0.1 mm，偏心距为0.08 mm，偏心率为0.8，偏位角为45°，转速为1 200 r/min，轴承的宽度为2 mm。轴承套材料设置为高分子聚合物，参数为：泊松比0.4，弹性模量1 GPa。润滑剂选择为水。如图1(b)所示，为矩形-半球型的复合型织构模型，第一层孔宽为W，第一层孔深为D，第二层织构半径为R。

1.2 网格划分

如图2(a)所示为用于流场分析的轴承水膜模型与网格划分。该模型的网格质量系数的平均值约为0.76，偏斜系数的平均值约为0.32。如图2(b)所示为用于固体分析的轴承轴套模型与网格划分，该模型的网格质量系数的平均值约为0.83，偏斜系数的平均值约为0.24。网格的质量会影响仿真分析结果，文中模型的网格质量较好。

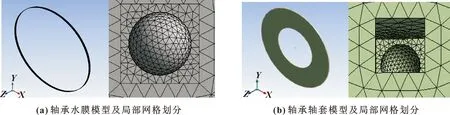
图2 模型的网格划分

1.3 控制方程与边界条件设置

对于不可压缩的黏性流体，其Navier-Stokes(N-S)方程为

(1)

对于外筒静止内筒旋转的模型，根据雷诺公式，计算出临界雷诺数为

(2)

实际雷诺数可由下式计算：

(3)

式中:v表示水的流速，取v=4 m/s；h表示水膜厚度，m。

经计算可知实际雷诺数远大于临界雷诺值，故判定该模型为紊流模型。文中选用常用的标准k-Epsilon紊流模型。

文中重点研究轴承的承载力、摩擦力以及摩擦因数。轴承承载力计算如公式(4)—(6)所示。

Wx=∬Aprcosαdαdz

(4)

Wy=∬Aprsinαdαdz

(5)

(6)

式中:p为水膜压力，Pa；r为轴的半径，m；α为轴承沿周向的角度，(°)；A为水膜与轴承间的流固耦合的面积，m2。

对水膜的剪切应力进行积分可以得出水膜的摩擦力，如公式(7)—(9)所示。

Ffx=∬Aτrsinαdαdz

(7)

Ffy=∬Aτrcosαdαdz

(8)

(9)

式中：τ为水膜的剪切力，Pa。

由式(6)、(9)计算所得的水膜承载力和摩擦力，按公式(10)计算摩擦因数。

(10)

假设所有算例均不考虑气穴现象。设置边界条件如图3所示，具体设置为

图3 边界条件

(1)设置流体内壁面为无滑移壁面边界条件，绕Z轴顺时针转动，转速为1 200 r/min；

(2)忽略流体进口区和出口区的压力差，2个区域的压力均为101 kPa；

(3)设置流体的外壁面为壁面边界条件，流体的外壁面与固体的内壁面发生接触，因此，流体外壁面设置流固耦合边界条件，固体内壁面设置为接触面；

(4)固体的外壁面设置为固定边界条件。

2 结果分析与讨论

2.1 计算模型有效性验证

为了保证仿真结果的准确性，按文献[20]设定几何参数、控制方程、边界条件及网格划分方法，但设定其工作条件与文中的复合型织构轴承一致。图4所示为文中模型与文献[20]模型的压力对比。

图4 文中模型与文献[20]压力对比

如图4所示，文中模型的水膜周向压力变化趋势与文献[20]模型的趋势基本吻合，水膜压力的最大值和最小值的集中区域也相同，表明文中采取的计算模型和计算方法较为合理，结果可靠。

2.2 织构位置对摩擦性能的影响

单层织构模型和复合型织构模型的第一层孔深D取0.7 mm，第一层孔宽W为0.5 mm，复合型织构模型第二层孔半径R为0.2 mm，转速为1 200 r/min，织构间隔为5°，织构个数为8个。织构位置角度沿圆周方向，逆时针方向分布在轴承高压区的0°、22.5°、45°、67.5°、90°处。图5所示为光滑轴承、单层织构轴承以及复合型织构在轴承不同位置的最大水膜压力变化趋势。

图5 光滑轴承、单层织构与复合型织构轴承最大水膜压力对比

从图5可知，随着织构位置角度的增大，织构轴承的最大水膜压力呈先增加后减小的趋势,并且织构轴承的水膜压力始终大于光滑轴承；复合型织构在织构位置角度为45°时，织构轴承的最大水膜压力值达到最大，该处为复合型织构水膜压力最优处。圆周位置小于45°区域为轴承压力下降区，由于织构会增大轴承的水膜厚度，且复合型织构所增加的水膜厚度大于单层织构，因此，尽管复合型织构能够产生多次动压效应，由于膜厚的影响，复合型织构的最大水膜压力值会小于单层织构。而在圆周位置大于45°区域，织构位于压力升压区，有助于轴承的动压效应，复合型织构的水膜压力大于单层织构。而这也是织构轴承的最大水膜压力呈先增加后减小趋势的原因。

图6所示为光滑轴承、单层织构轴承以及复合型织构在轴承不同位置的摩擦力变化趋势。

图6 光滑轴承、单层织构与复合型织构轴承摩擦力对比

如图6所示，随着织构位置角度的增大，织构轴承的摩擦力呈先减小后增大的趋势，并且织构轴承的摩擦力始终小于光滑轴承。对比单层织构与复合型织构的摩擦力变化趋势，复合型织构轴承的摩擦力值始终最低。在织构位置为45°时，轴承的摩擦力值最小。

图7所示为光滑轴承、单层织构轴承以及复合型织构在轴承不同位置的摩擦因数变化趋势。

图7 光滑轴承、单层织构与复合型织构轴承摩擦因数对比

如图7所示，随着织构位置角度的增大，织构轴承的摩擦因数总体呈先减小后增大的趋势，并且织构轴承的摩擦因数值远小于光滑轴承。在织构位置为45°时，织构轴承的摩擦因数值最小，且复合型织构的摩擦因数远低于单层织构。织构位置角度在0°～22.5°和67.5°～90°范围内，织构轴承的摩擦因数值随位置角度的变化不明显；而在22.5°～67.5°范围内，织构轴承的摩擦因数值随位置角度的变化显著，复合型织构的摩擦因数值受织构位置的变化影响大于单层织构。由于复合型织构的深度较大，在水膜厚度突变处出现微小旋涡，而织构内的旋涡方向与流向相反，能够降低织构所在表面的切应力，降低表面摩擦力。因此，产生了图6、7所示的变化情况。

结合图5—7可得出，合适的织构位置对复合型织构的最大水膜压力值影响较大。因为织构位置角度在超过22.5°～45°范围内的某一角度后，复合型织构的水膜压力开始超过单层织构。而复合型织构轴承的摩擦力和摩擦因数始终小于单层织构轴承。

2.3 织构间距对摩擦特性的影响

复合型织构模型中孔深D为0.7 mm，第二层孔半径R为0.2 mm，第一层孔宽W为0.5 mm。图8所示为随着织构位置角度的改变，不同间距条件下复合型织构最大水膜压力的变化情况。

如图8所示，在不同复合织构间距条件下，随织构位置角度的增大，复合型织构的最大水膜压力呈先上升后下降的趋势。这与上述仿真试验得出的结果相同。但织构间距为9°时，在织构位置角度为45°处水膜压力值出现小幅度下降。在织构间距为7°～9°时，出现最优水膜压力的位置在间距位置角度为67.5°处，而在该位置时，水膜压力最优的间距为7°。而在织构位置角度为45°处出现水膜压力最大值的织构间距为6°。

图9所示为随着织构位置角度的改变，不同间距条件下复合型织构轴承摩擦因数的变化情况。

图9 不同间距的复合型织构轴承摩擦因数随织构位置角度变化

如图9所示，在不同织构间距条件下，随织构位置角度的增大，复合型织构的摩擦因数总体呈先下降后上升的趋势。这与上述摩擦因数的变化结果相同。并且在织构位置为45°时，摩擦因数最优的织构间距为5°。对比不同织构间距轴承的摩擦因数在不同织构位置角度的变化趋势可知,在织构间距为5°时的摩擦因数的变化趋势最为剧烈。结合图8和图9可知，为了能获得较高的承载能力和较小的摩擦因数，较为合适的织构间距应为5°，这主要是因为微造型间距较小时，微造型之间的协同效应更明显。

流迹线图能够反映流体在流场中的流动状态，处于同一条流线上的质点运动方向与该点处流线的切线方向相同[23]。为了解释织构位置为45°时的变化情况，以图10所示的织构位置为45°的复合型织构的流迹线图进行解释。

由图10可知，在织构位置角度为45°时，随着织构间距的改变，复合型织构内的旋涡强度发生改变。在织构间距为5°时，织构内上部的旋涡完全形成，但旋涡体积占比较小，织构底部的旋涡尚未形成。在织构间距为6°时，织构内上部的旋涡体积占比较大，但上部新的织构旋涡开始逐渐形成，织构底部的旋涡尚未形成。由于旋涡尚未形成时，织构内的流体动压效应占主导。因此，在织构间距为6°时，织构内未形成的旋涡较多，该条件下的水膜压力值最大，承载能力最好。如图10(c)所示，在织构间距为8°时，织构内上部的旋涡体积较小，织构底部的旋涡尚未形成。而如图10(d)所示，在织构间距为9°时，织构内上部的旋涡体积占比开始增大，且下部的织构旋涡已开始形成。因此，织构间距为9°时的水膜压力值最低。

图10 不同复合织构间距下的流迹线

为了解释复合型织构的水膜压力和摩擦因数随织构位置的变化，以图11所示的织构间距为5°的复合型织构的流迹线图进行解释。

图11 不同复合织构位置角度下的流迹线

由图11可知，在织构间距为5°时，随着织构位置角度的改变，复合型织构内的旋涡强度发生改变。由图11(a)—(c)可知，随着织构位置角度的改变，织构内的旋涡尺寸和体积占比逐渐减少，并伴随有新的旋涡开始生成；而由图11(c)—(e)可知，随着织构位置角度的增加，织构内的旋涡尺寸和体积比逐渐增大，旋涡数量有所减少。由于织构旋涡体积的增大，会降低轴承的承载能力。因此，在织构位置角度为0°～45°范围内，水膜压力值逐渐增大；在织构位置角度为45°～90°范围内，水膜压力值逐渐降低。

3 结论

通过改变复合型织构在水润滑轴承高压区的位置和织构间距,采用流固耦合的方法研究不同复合织构轴承的摩擦学性能，分析复合型织构在不同位置和间距条件下水膜压力和摩擦因数的变化规律。主要结论如下：

(1)随着织构位置角度的改变，复合型织构轴承的摩擦力和摩擦因数始终小于单层织构轴承。而织构位置角度在超过22.5°～45°范围内的某一角度后，复合型织构轴承的水膜压力开始超过单层织构。因此，对于复合型织构而言，位置角度的选择对水润滑轴承的承载能力更为重要。

(2)在不同间距条件下，随着织构位置角度的增大，复合型织构轴承的最大水膜压力呈先增加后减小的趋势；复合型织构轴承的摩擦因数呈现先减小后增加的趋势。结合不同间距条件下随织构位置改变的织构轴承水膜压力和摩擦因数变化趋势，在织构间距为5°且织构位置角度为45°时，复合型织构轴承的摩擦学性能最优。