不受姿态误差影响的惯性/磁感应融合定位方法

2022-11-11李新年李清华王常虹郑元勋王振桓夏子权

中国惯性技术学报 2022年4期

李新年，李清华，王常虹，郑元勋，王振桓，夏子权

（1.哈尔滨工业大学空间控制与惯性技术研究中心，哈尔滨 150001；2.中国兵器工业集团航空弹药研究院，哈尔滨 150030）

科技的高速发展在便捷人类生活、拓展人类生存空间的同时，对现有技术提出了更高的功能与指标。导航定位技术作为一种基础技术，在物联、机器人等新兴研究领域中起着重要的作用[1,2]，然而由于室内等复杂场景存在非视距、多径等影响因素，现有GPS、UWB等技术难以实现无累积误差的高精度定位服务。根据电磁信号的波粒二象性可知，磁场穿透能力与频率成反比，因此基于高穿透低频磁场的定位方法是实现室内场景高精度定位的有效方案之一[3-5]。低频磁场定位信号一般由通电螺线管、旋转永磁体等人工磁信标产生，经分析，其在空间的磁场分布与相对位置存在确定性数值关系，基于此，本文提出了一种磁感应室内定位方法。

基于人工磁信标的磁感应定位方法主要围绕磁感应强度、磁感应矢量[6-17]两个角度开展研究。磁感应强度所提供的定位信息少于磁感应矢量，因此基于磁感应矢量的人工磁信标定位系统的复杂度通常要低于基于磁感应强度的定位系统。然而基于磁场矢量的磁信标定位系统受传感器姿态影响，通常需要结合其它辅助信息来获取姿态信息，进一步解算目标位置。基于惯性传感器[6-11]、多磁信标/传感器的几何信息[12-17]常被用来辅助磁信标定位系统，如Pasku等人[9]利用磁强计与惯性传感器设计了一种组合导航系统，惯性传感器通过敏感姿态数据辅助磁传感器转换磁感应矢量，并结合磁场分布模型与空间几何构型建立磁信标定位模型，实现对目标位置的估计；郑元勋等人[12-14]采用多个位置姿态已知的人工磁信标构建出具有明确几何信息的磁感应定位系统，达到对目标位置姿态的估计。然而辅助信息源的设计不仅增加了系统的复杂度，而且直接从其它信息源获取的姿态信息被用来转换磁感应矢量时，其姿态误差会对磁感应定位精度造成影响。

为解决磁信标定位系统受传感器姿态误差影响的问题，本文建立了一种与传感器姿态无关的磁信标定位模型；并基于此，结合惯导模型提出了一种改进的惯性/磁感应的定位方法，通过无迹卡尔曼滤波[18-20]（Unscented Kalman Filter,UKF）算法和磁信标磁场数据实现了对惯导一步预测结果的修正，提高了定位精度、定位结果的输出速度和稳定性。

1 磁感应定位模型

1.1 双轴磁信标定位模型

人工磁信标系统主要由磁源、传感器与导航解算单元三部分构成，而由磁源产生的低频磁场又是定位信息的传播媒介，其分布规律是分析定位方法的理论基础。本节将结合毕奥-萨伐尔定律与磁偶极子模型对双轴磁信标的磁场分布进行理论分析。依据磁偶极子模型将通电螺线管视为圆形载流回路，当环境中的磁导率为0μ，通电螺线管的激励电流幅值为I，信号频率为ω，线圈匝数为N，则根据毕奥-萨伐尔定律，磁偶极子磁矩指向与信标坐标系中z轴的指向相同时，空间中任意一点处P（x,y,z）单轴螺线管的磁感应矢量的表达式为：

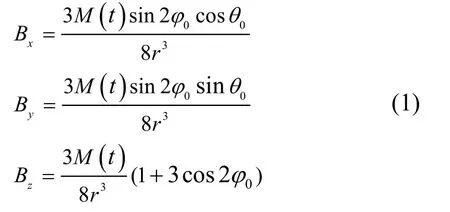
其中r为目标点P到坐标原点O的相对距离，为俯仰角，为相对方位角[5]，为通电螺线管磁矩，人工磁信标与目标点之间的相对位置如图1所示。

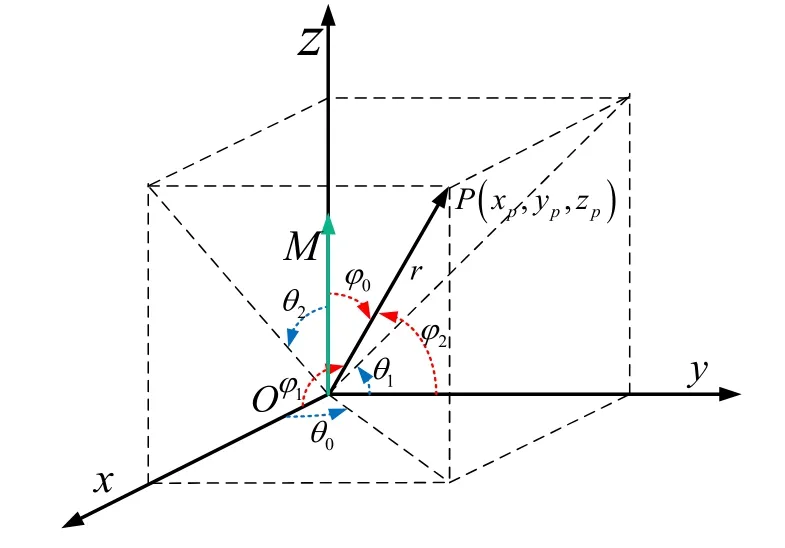
图1 信标中心与目标点之间的相对方位Fig.1 Relative position from center of beacon to the target

图中1φ、2φ、0φ分别为磁信标与目标点之间相对于x轴、y轴、z轴的俯仰角，1θ、2θ、0θ分别为磁信标与目标点之间相对于x轴、y轴、z轴的偏航角，根据长方体中的边角关系，可以获得如下转换关系：

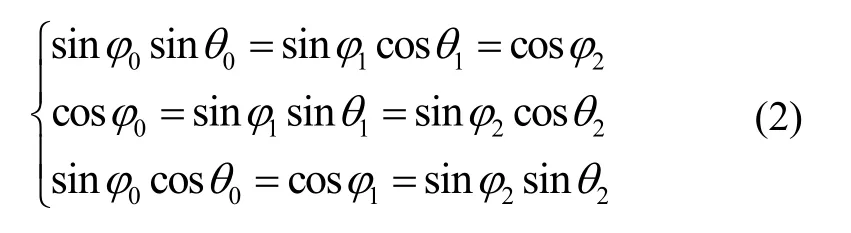
根据螺线管轴数，常见的磁信标可以分为单轴磁信标、双轴磁信标和三轴磁信标；基于磁场矢量的单轴磁信标不足以实现定位，而三轴磁信标存在成本高、空间结构复杂等缺点，因此本系统采用双轴正交螺线管磁信标作为磁源，其空间结构如图2所示。

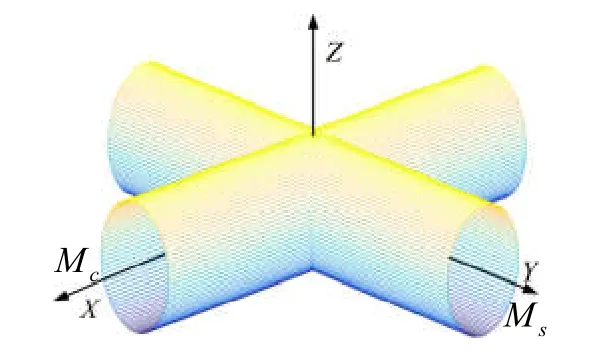
图2 双轴磁信标结构形式Fig.2 The structure of dual-axis magnetic beacon

基于单轴螺线管的磁感应矢量表达式(1)、相对方位角之间的转换式(2)以及双轴磁信标结构形式，双轴磁信标中两个通电螺线管在空间中点产生的磁场可以分别表示为：

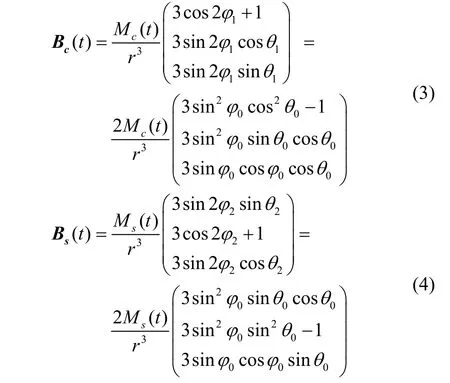
依据双轴磁信标在空间中任意一点的磁场矢量表达式和高维空间中椭圆的基本方程可以分析出，空间中任意一点的磁场矢量随时间呈椭圆平面变化，该椭圆平面具有唯一方向不变的特征矢量，该特征矢量可以通过式(5)进行提取。

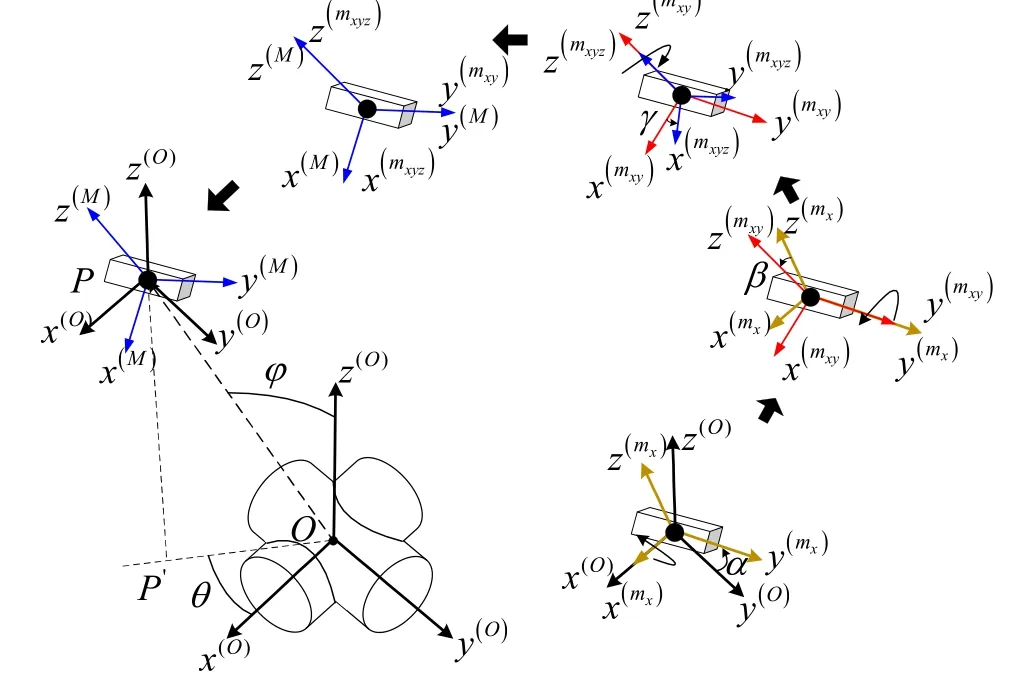
图3 传感器坐标转换过程Fig.3 Process of magnetic sensor attitude translation

为避免传感器载体坐标系与信标坐标系不一致对定位精度的影响，根据几何理论中矢量内积相关知识，可以得到如下不受影响的磁场矢量与位置相关表达式：

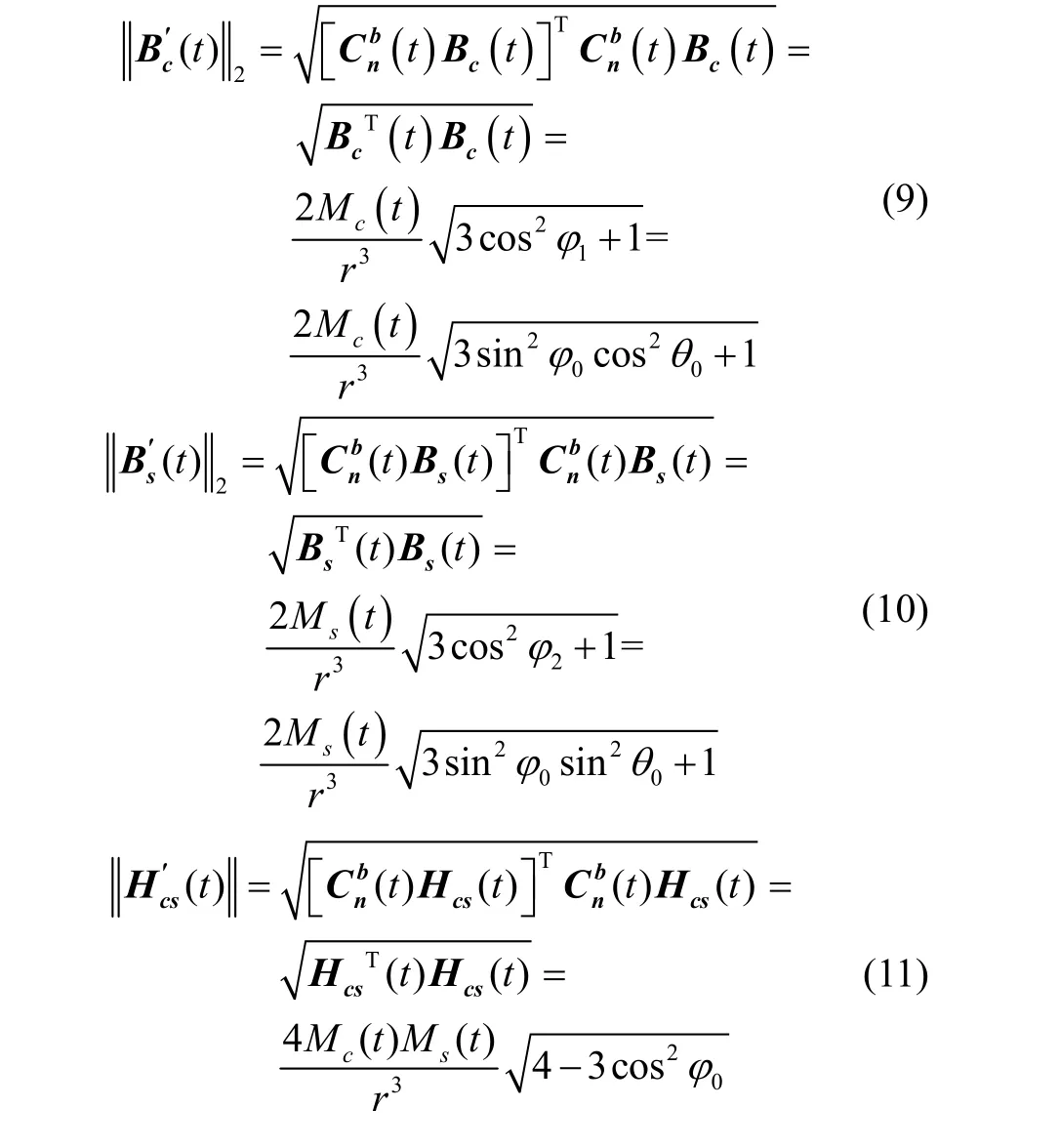
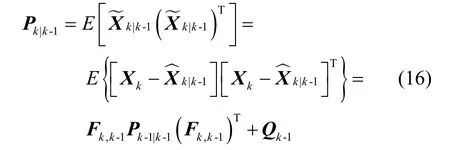
根据磁场传播特性，式(9)-(11)可以简化为双对数表达式：

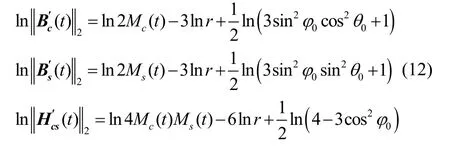
基于式(12)，可以构建如下定位模型：

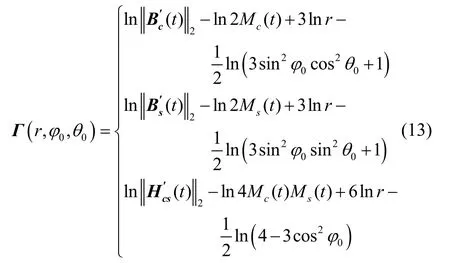
1.2 基于UKF的惯性/磁感应定位

基于磁场分布规律，本文在1.1节分析了一种不受传感器姿态影响的双轴磁信标定位模型，能够以较高的精度实现对静态目标位置的估计，然而磁信标定位方法往往需要整周期的磁场数据解算目标位置，输出速度不能满足动态目标需求，因此本文基于无迹卡尔曼滤波算法提出了一种融合惯性数据和磁感应矢量的定位方法，惯性/磁感应定位模型可以表示为：

改进的惯性/磁感应定位模型是一种不存在累计误差的定位模型，惯性元件的一步预测误差是由器件自身的零偏、随机游走、标定误差等因素造成的，是一种随时间逐渐增加的累计误差。短时间内，惯性元件的一步预测结果接近真实位置，能够为磁感应定位方法求解目标位置提供参考值，而低频磁场定位模型能够实现对惯性元件的一步预测结果的修正，二者的融合使惯性/磁感应定位方法的误差在一定范围上下波动。

根据式(14)可以分析出，利用惯性/磁感应技术对动态目标进行定位的过程可以被建模成典型的非线性动态模型。EKF、UKF及智能优化（群智能）算法是解决非线性动态系统问题的主流方法，EKF是一种利用函数近似的思路进行非线性滤波的方法，由于EKF对非线性强度高的系统滤波存在较大模型误差；智能优化算法是利用多个智能体的自身状态与目标状态之间的差距不断调整、优化自身以实现对目标状态进行最优估计的一种搜索方法，存在寻优速度较慢，每一次寻优需要遍历所有智能体后才能完成，计算资源需求高等问题。UKF是一种对后验概率密度进行近似的次优滤波算法，降低了系统模型误差，且能够以较少的计算资源和较高的计算效率逼近非线性系统的结果。因此，采用UKF算法对惯性/磁感应模型进行滤波估计，在保证定位精度的同时，提升计算效率。

根据惯性/磁感应定位模型(14)，系统状态噪声kV与量测噪声kW无关，且为零均值高斯白噪声，则一步预测误差协方差为：

进行Sigma采样，并对磁感应矢量进行一步预测：

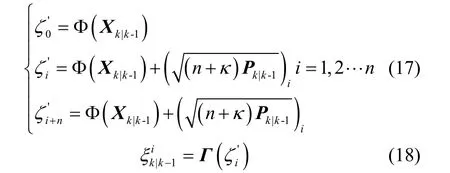
磁感应矢量的一步预测均值、量测预测误差协方差以及状态预测误差和量测预测误差的互协方差为：

基于UKF的惯性/磁感应定位方法流程图如图4所示。

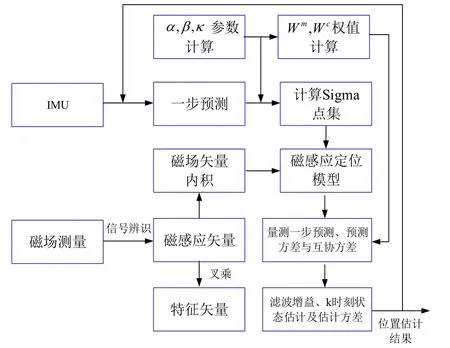
图4 惯性/磁感应定位流程图Fig.4 Inertial magneto-i nductivepositioning flow chart

2 实验验证

不受传感器姿态影响的磁感应定位模型与基于UKF的惯性/磁感应融合定位方法为本文的两个主要研究目标，本节将通过实验的方式对磁感应定位模型有效性和精度进行验证，由于实际测试过程中目标的真实动态轨迹很难给出，因此本节将采用数值仿真的方式对惯性/磁感应定位方法进行仿真验证，将文献[9]中IMU解算的姿态辅助磁信标定位方法与本文提出的改进惯性/磁感应定位方法对动态目标的运动轨迹估计结果与真实轨迹进行对比，从而达到验证基于UKF的惯性/磁感应定位方法精度的目的。

2.1 磁感应定位模型实验验证

本节将利用如图5所示的双轴磁信标实验系统测试磁感应定位模型，整个系统由信号生成单元、线性功率放大器、双轴磁信标、磁传感器探头与数据处理模块、定位解算计算机5部分构成，激励电流幅值均为4 A、频率均为20Hz，相位相差90°，磁传感器感知范围为0.1 nT-10000 nT，磁信标轴线长度为35cm，螺线管直径为15cm。系统导航坐标系以磁信标几何中心为原点，磁信标坐标系与全局坐标系重合，磁传感器在全局坐标系第一象限内，坐标系指向与图5中坐标轴一致。实验过程中磁信标底面与传感器之间的高度相差0.82m，传感器位置每次向x轴或y轴移动0.6m，在同一位置处传感器采集3次磁场矢量，磁传感器所在的坐标系与磁信标所在坐标系的偏航角分别成0°、60°和120°角度，输入定位解算计算机中进行解算，以测试不受传感器姿态影响的磁感应定位模型有效性与定位效果。

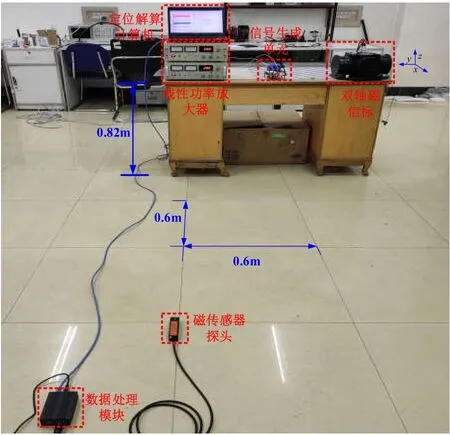
图5 实验系统Fig.5 Experimental system

根据式(13)的非线性磁感应定位模型对磁传感器位置进行估计，利用Levenberg-Marquardt方法通过迭代的方式估计非线性方程组最优解，实验结果如图6所示，第1组磁场矢量解算结果为传感器坐标系与信标坐标系一致时（即偏航角夹角为0°）的位置估计，第2、3组为传感器坐标系与磁信标坐标系夹角分别为60°和120°时的估计结果。根据以上实验的结果可以看出，利用磁感应定位模型能够准确地估计出传感器与磁信标之间的相对位置，且位置估计结果不受传感器姿态的影响。

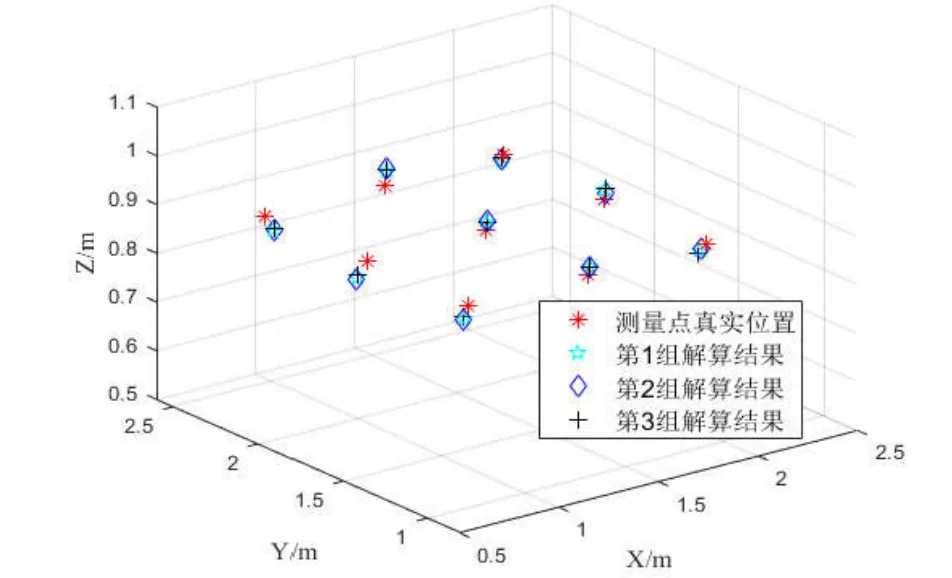
图6 静态目标定位结果Fig.6 Positioning resultsof static tar get

2.2 惯性/磁感应定位方法数值仿真验证

在前一节实验中验证了本文提出的磁感应定位模型的可行性，本节将通过数值仿真的方式验证基于UKF的惯性/磁感应定位方法。设IMU和磁传感器是坐标系一致的刚性连接，两者之间质心重合，磁场数据包括磁信标磁场、地磁场和环境中干扰磁场，磁信标磁场数据由磁偶极子模型和估计的双轴螺线管磁矩参数产生，短时间内磁场数据可以视为常值，根据实验室测量地磁场强度约为40000 nT，干扰磁场可视为白噪声约为0.5 nT，磁传感器信号采样率为1000 Hz，惯性元件指标为：（1）加速度计的零偏不稳定性为9.8 ×10-2m/s2；（2）陀螺仪的零偏不稳定性为8 °/h；（3）惯导数据输出速率为1000 Hz。依据上述数据模型和相关参数，以给出的实际路径为基础生成磁场数据和惯性导航系统数据。该仿真将文献[9]中的传统惯性/磁感应定位方法，即通过IMU解算的姿态信息对磁场矢量进行转换再进行融合定位的方法，与本文提出的不受传感器姿态影响的改进惯性/磁感应定位方法进行对比分析，以达到验证磁感应定位模型有效性和测试惯性/磁感应定位方法性能的目的。

仿真结果表明，结果输出速度方面：由于仅依靠磁感应定位方法需要整周期的磁场数据进行位置解算，位置结果的输出频率低于20 Hz；本文提出的惯性/磁感应定位方法结果解算时间低于8 ms，即输出频率高于125 Hz，惯性/磁感应融合定位方法提高了磁感应定位方法的位置估计结果输出速度。定位精度方面：数值仿真误差如图7所示，两种定位方法误差的累积概率分布如图8所示。

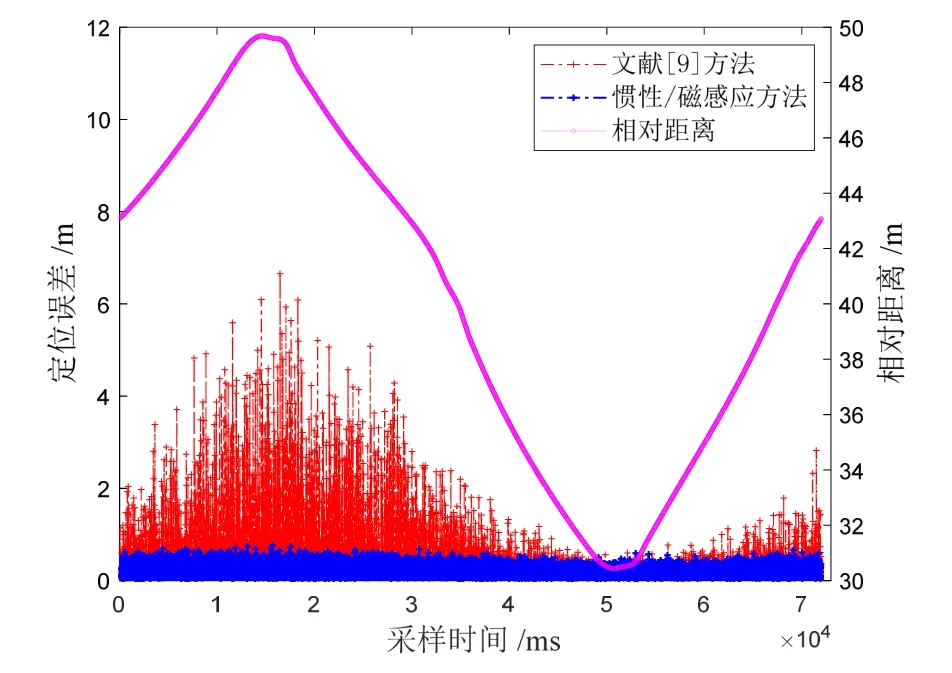
图7 动态目标定位误差Fig.7 Positioning errors of moving target

动态目标定位误差和误差累积概率分布的结果表明，惯性/磁感应融合定位方法能够避免累计误差，且本文提出的改进惯性/磁感应定位方法与文献[9]采用的传统惯性/磁感应定位方法相比，传统的惯性/磁感应融合方法定位误差随着相对距离的增加而增大，由式(13)分析可得出：随着距离的增长，磁场信号信噪比降低，姿态解算误差对磁信标定位方法的影响增大。在磁信标有效作用域内，本文提出的方法定位性能优于传统惯性/磁感应方法，不会受传感器姿态解算误差的影响，定位结果在一定范围内成上下波动的变化。误差累积概率分布如图8所示。

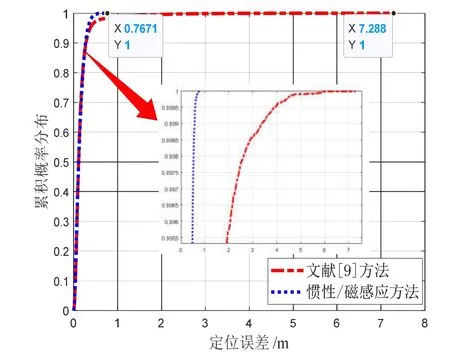
图8 动态目标定位误差累积概率分布Fig.8 The cumulative probability distribution of moving target positioning errors

文献[9]和本文提出方法的定位误差低于0.5 m的

概率为95%，文献[9]方法最大估计误差为7.3 m，本文提出的基于UKF惯性/磁感应融合方法的最大估计误差为0.77 m。由此看出在磁场信号信噪比低于一定程度时，传感器姿态误差对磁信标定位方法造成的影响增大，而本文提出的惯性/磁感应定位方法一方面避免了传感器姿态对系统定位的影响，另一方面实现了惯导数据与磁感应数据的融合，提升了系统定位性能。