重力扰动对极区下高精度惯导系统的影响分析及补偿

2022-11-11王德昭吉宇人崔文婷奔粤阳宋欣萌

中国惯性技术学报 2022年4期

李倩，王德昭，吉宇人，崔文婷，奔粤阳，宋欣萌

（1.哈尔滨工程大学智能科学与工程学院，哈尔滨 150001；2.中国船舶工业集团公司第七〇八研究所，上海 200011）

随着极区航线的不断开拓，极区导航能力成为船舶、飞机等运载体在极区安全航行的重要技术支撑。捷联惯性导航系统（Strapdown Inertial Navigation System,SINS）以其良好的自主性和可靠性成为极区导航技术的研究重点。由于常规捷联惯性导航系统机械编排在极区存在无北向基准、经线圈快速汇聚等问题，国内外学者相继提出自由方位、游移方位、格网坐标系参考框架以及横坐标系参考框架等适用于极区工作的惯性导航机械编排[1,2]。目前，这些极区惯性导航机械编排及其初始对准算法、误差抑制方法在理论上相对成熟，极区惯性导航技术也正朝着高精度方向发展[3]。

在器件精度不高的惯性导航系统中，与加速度计误差相比，重力扰动对系统的影响可以忽略。但是随着惯性器件精度的不断提高与极区高精度惯性导航系统需求的发展，器件误差已不再是制约精度的核心因素，而当重力扰动与加速度计零偏处于同一量级，甚至高于后者时，重力扰动已成为不可忽略的误差源[5]。

文献[6]给出了一种高精度惯导系统重力扰动的阻尼抑制方法，但不适合载体大机动等应用场景。文献[7]通过将重力扰动建模成一阶马尔科夫模型，分析了其在惯性导航系统中的传播特性，并确定了重力扰动实时补偿对重力场球谐模型阶数的要求。文献[8]提出一种面向定位定向系统的高精度重力扰动补偿方法，实际飞行测试表明该方法可以有效提升姿态精度。文献[9]研究了基于EIGEN-6C4重力场球谐模型的高精度惯性导航系统重力扰动补偿方法。通过对现有文献分析可以看出，虽然国内外学者对重力扰动影响分析及抑制补偿技术的研究相对成熟，但对于横坐标系下重力扰动对高精度惯导系统的影响分析和补偿技术的研究鲜有报道。

考虑高精度惯性导航系统极区导航能力需求，本文以极区横坐标系下惯性导航系统机械编排为基础，推导出重力扰动矢量在横地理坐标系的投影关系。进一步，分别基于确定性常值重力扰动模型与随机模型定量分析了重力扰动水平分量对横坐标系捷联惯导系统的影响。在理论分析的基础上，利用三次样条插值法，基于2190阶EIGEN-6C4重力场球谐模型获取分辨率为1' ×1'的极区重力扰动数据，并补偿到横坐标系下惯导系统解算过程中，从而实现极区高精度惯导系统的重力扰动补偿。

1 重力扰动矢量建模

1.1 重力扰动

惯性导航系统通常基于地球参考椭球模型进行解算，但由于地球参考椭球模型与大地水准面不完全吻合，导致基于地球参考椭球模型得到的正常重力矢量与当地真实重力矢量g之间存在一定偏差，该偏差即为重力扰动δ g。如图1所示，真实重力矢量g、正常重力矢量g0及重力扰动矢量δ g三者之间关系为：

由于加速度计不能区分重力扰动和载体加速度，导致重力扰动给惯性导航解算带来一定误差。通常情况下，惯导系统高度通道的解算可以通过外部信息辅助实现，因此重力扰动对惯导系统的影响主要体现在水平分量上[10]。

如图1所示，真实重力矢量偏离正常重力矢量的角度称为垂线偏差。垂线偏差在卯酉圈方向上的分量称为东-西垂线偏差，记为η；垂线偏差在子午圈方向上的分量称为北-南垂线偏差，记为ξ。重力扰动在东北天（E-N-U）地理坐标系（记为t）投影分别记为，则重力扰动可以表示为[11]：

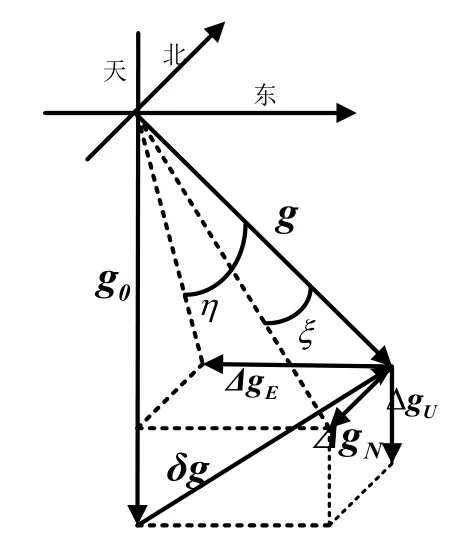
图1 重力扰动Fig.1 Gravity disturbance

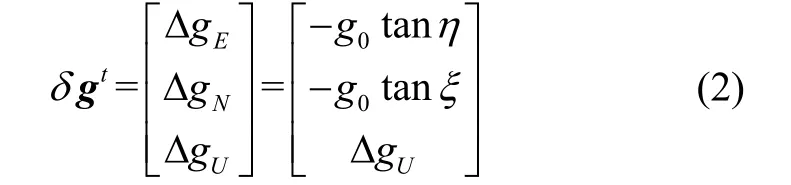
由于垂线偏差角度较小，式(2)可近似表示为：

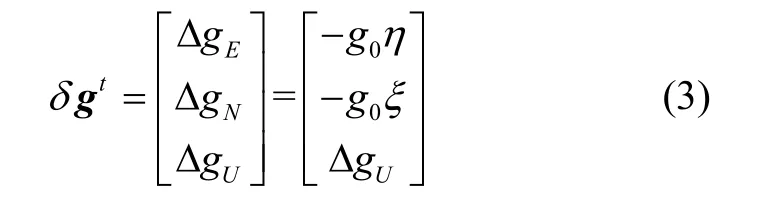
式中：正常重力大小可按式(4)计算得到：

式中：γ= 9.7803253，a= 0.0053022，b= 0.0000058，φ为当地纬度。

式中：λ为当地经度。

将式(6)代入式(5)可得重力扰动在横东北天地理坐标系水平方向投影与常规东北天地理坐标系投影，具有如下关系：

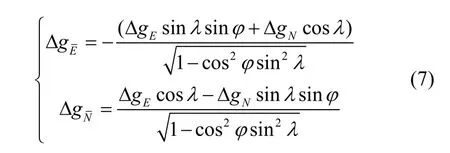
需要注意的是，由于常规东北天地理坐标系与横地理坐标系z轴重合，故。

1.2 重力场球谐模型

地球重力场球谐模型是表达地球质体外部重力位的一种函数模型，其利用“微元-积分”的方法推导地球球面上任意位置的重力势能（重力场）。结果中包含经纬度级数形式的系数，因此称为“谐波”或“调和”系数。模型系数的阶次越高，表达出的重力势能变化越精细。在精度要求不高的导航系统中，只需选用标准化二阶零次球形调和系数；在高精度导航系统中，则需要考虑更高阶次系数。

目前，常用重力场球谐模型包括EIGEN-6C4重力场球谐模型和EGM2008重力场球谐模型。与EGM2008相比，EIGEN-6C4突出的改进是增加了重力和海洋环流试验任务数据，其精度较EGM2008有所提高，更适用于惯性导航系统重力扰动补偿[4,13]。更为重要的是，EIGEN-6C4重力场球谐模型极区重力场数据比EGM2008相对更加准确[14]。因此，本文主要基于EIGEN-6C4重力场球谐模型开展极区重力扰动影响分析与补偿方法研究。

地球重力扰动位用球谐级数模型可表示为：

由于重力扰动矢量使用球坐标表示，而导航坐标系为东北天地理坐标系，因此需将其转换到东北天地理坐标系中，其转换关系可表示为：

将式(10)代入式(11)即可得到由球谐函数表达的重力扰动矢量：

进一步，将式(12)代入式(7)，即可根据EIGEN-6C4重力场球谐模型计算横地理坐标系下重力扰动矢量的水平投影，进而分析其对横坐标系捷联惯性导航系统的影响。

2 重力扰动对横坐标系惯导系统影响分析

2.1 基于确定性模型的重力扰动影响分析

根据横坐标系惯性导航系统工作原理可知，其解算比力方程为：

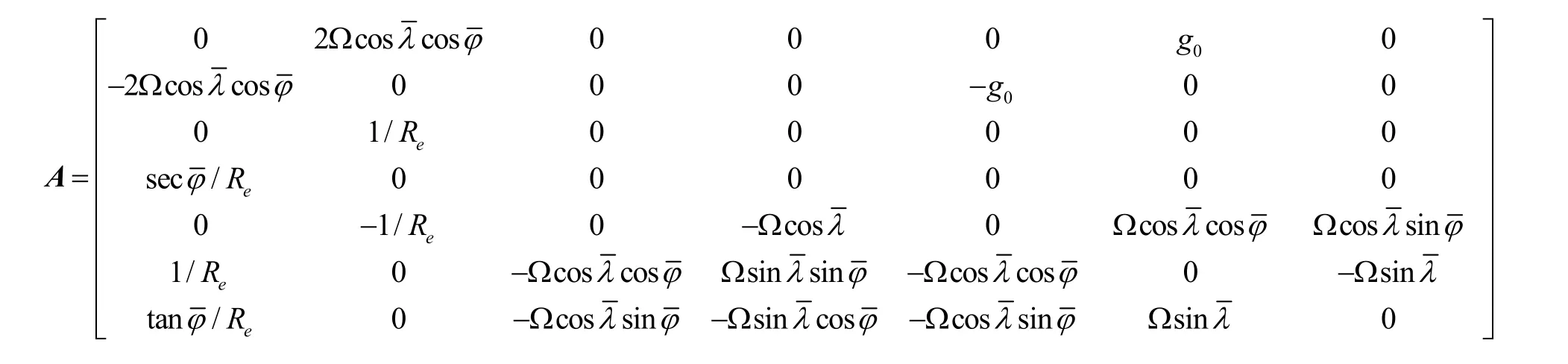
根据上述推导可知：重力扰动水平分量在横坐标系捷联惯性导航系统中的误差传播通道与加速度计零偏相同，故可将其等效为加速度计零偏。根据式(18)可得矩阵方程的解为：

以横经度误差为例，根据式(19)推导得出其与重力扰动水平分量之间的传递函数为：

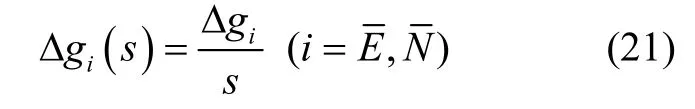
将式(21)代入式(20)，进一步根据终值定理可以得到重力扰动水平分量引起的横经度误差稳态值为：

同理，可以得到重力扰动水平分量引起的其他导航误差稳态值如表1所示。

表1 重力扰动水平分量引起的导航误差稳态值Tab.1 Steady-state values of navigation errors caused by horizontal gravity disturbance

由表1可以看出，在横坐标系下，重力扰动水平分量引起的惯导系统误差与常规坐标下的规律一致，即导致系统产生振荡性误差的同时，还产生如表1所示的常值偏差。

2.2 基于随机模型的重力扰动影响分析

2.1节中，将重力扰动等效为确定性常值，分析横坐标系下其对惯导系统的影响。但考虑到真实重力场不仅随着位置变化而变化，同时其也是一个时变连续函数，所以分析横坐标系下重力扰动随机模型对惯导系统的影响十分必要[15]。已有研究表明，在齐次、各向同性假设条件下，若已知重力扰动方差，则可用一阶或高阶马尔科夫模型建立重力扰动随机模型[16,17]。

以横东向回路为例，分析随机重力扰动引起的系统误差。为直观表示重力扰动在水平方向的影响，将式(20)左右同时乘以，进一步化简可以得到横东向重力扰动与水平位置误差之间的传递函数为：

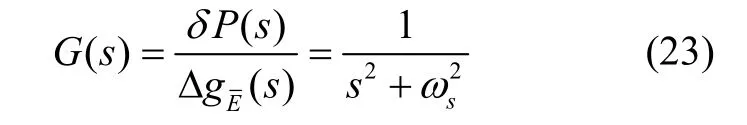
根据式(23)可以得到横东向重力扰动激励的水平位置误差时域表达式如式(24)所示。

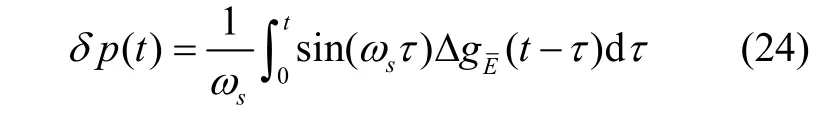
进一步，对式(24)求数学期望，可以得到水平位置误差的均方误差为：

将式(26)代入式(25)，得到横坐标系捷联惯导系统水平位置误差的均方误差为：

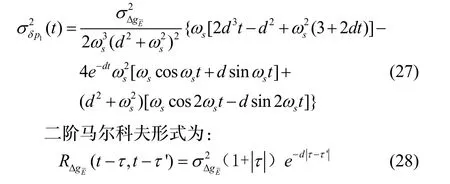
同理，将式(28)代入式(25)，得到横坐标系捷联惯导系统水平位置误差的均方误差为：

三阶马尔科夫形式为：

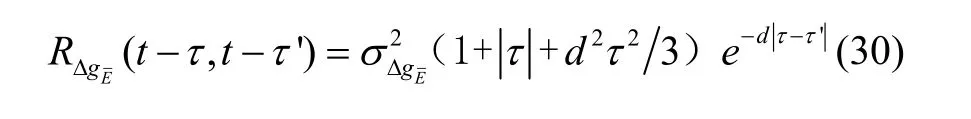
同理，将式(30)代入式(25)，得到横坐标系捷联惯导系统水平位置误差的均方误差为：

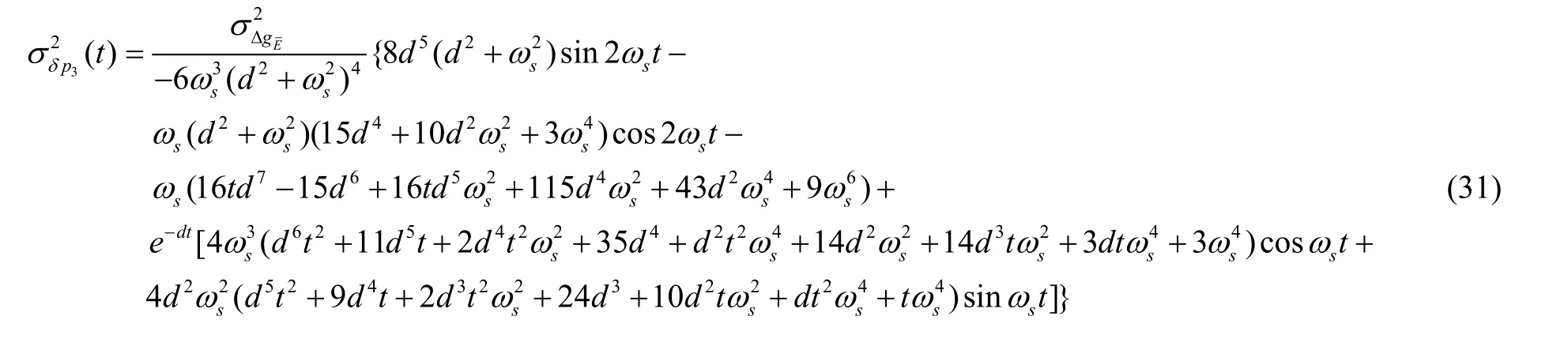
由式(27)(29)(31)可以看出，与确定性常值重力扰动引起的系统误差相比，马尔科夫随机重力扰动除会引起振荡性与常值误差以外，还包含随时间累积的误差项。但需要注意的是，无论哪种误差形式，其大小都与重力扰动方差成正比。

进一步，对马尔科夫随机重力扰动引起的横坐标系下惯导系统水平位置误差进行定量分析。根据现代船舰航行速度，分别选择速度为10、20、30、40（nmile/h），分析横东向重力扰动引起的位置均方根误差随相关距离和速度的变化如图2所示。

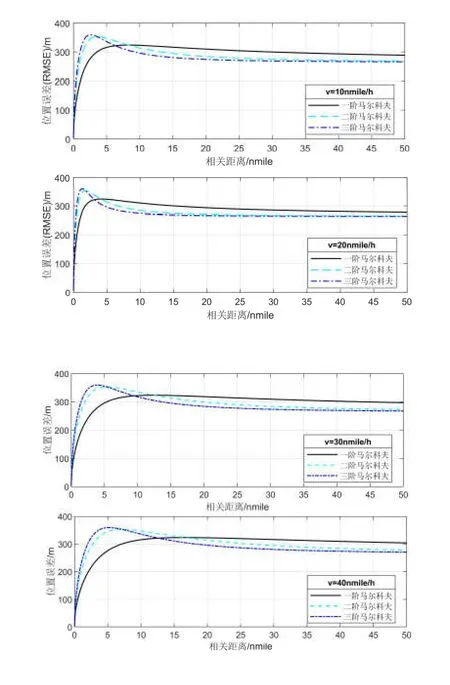
图2 不同航速对应的位置误差与相关距离关系Fig.2 Relationship between position error and correlation distance with different speed

由图2可以看出，随着速度增加，位置误差最大值所对应的相关距离越大。除此之外，与一阶马尔科夫模型相比，二阶与三阶马尔科夫随机重力扰动引起的位置误差最大值所对应的相关距离更小。

将EIGEN-6C4地球重力场球谐模型提供的2190阶调和系数与代入式(12)，计算极区某区域（经度120 °E~125 °E，纬度65 °N~90 °N）重力扰动在东北天地理坐标系水平投影分量，如图3所示。进一步，根据式(7)计算同一区域重力扰动在横东北天地理坐标系水平投影分量，如图4所示。图3-4分辨率为5'5'×，具体统计特性如表2所示。

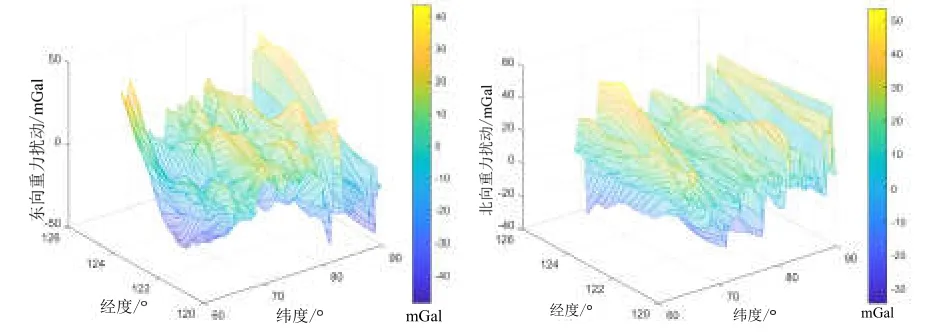
图3 重力扰动在东北天地理坐标系水平投影分量Fig.3 The horizontal projection of gravity disturbance in the East-North-Up geographic coordinate system

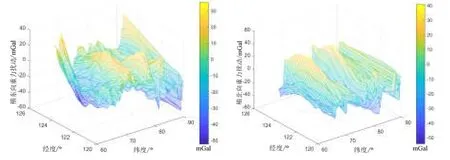
图4 重力扰动在横东北天地理坐标系水平投影分量Fig.4 The horizontal projection of gravity disturbance in the transversal East-North-Up geographic coordinate system

由表2可知，重力扰动在东北天地理坐标系与横东北天地理坐标系水平投影的平均值及均方差具有互补性。以平均值为例，当重力扰动在横东向投影相对东向投影增大时，横北向投影相对北向投影减小。下一步，根据极区重力扰动统计特性定量分析其引起的横坐标系捷联惯导系统水平位置误差。

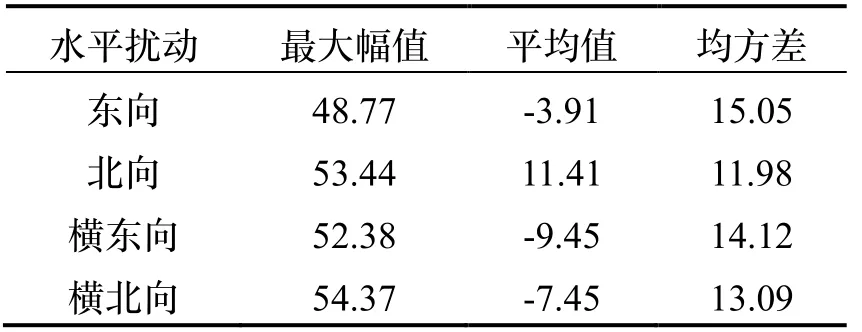
表2 重力扰动水平分量统计特性（单位：mGal）Tab.2 Statistical characteristics of horizontal gravity disturbance

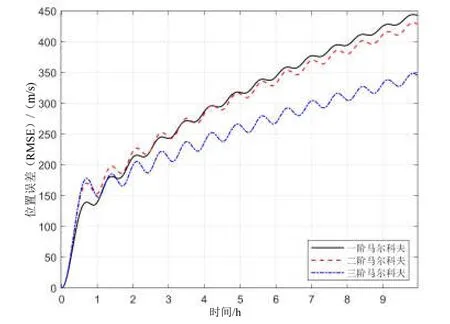
图5 横东向重力扰动引起的位置误差Fig.5 Position error caused by the eastward projection of gravity disturbance in the transversal geographic coordinate system

与上述分析过程类似，可以进一步通过推导横纬度误差与横北向重力扰动水平分量之间的传递函数分析横北向重力扰动水平分量对水平位置误差的影响，由于推导结果与式(23)表达形式一致，所以此处不再赘述。根据表2取横北向重力扰动方差，其他仿真条件与前述一致，从而得到横北向重力扰动引起的水平位置误差如图6所示。

图6 横北向重力扰动引起的位置误差Fig.6 Position error caused by the northward projection of gravity disturbance in the transversal geographic coordinate system

同理，可得速度v= 10 nmile/h、30 nmile/h、40 nmile/h时，一阶、二阶及三阶马尔科夫随机重力扰动水平分量引起的位置误差。由于篇幅限制，此处不单独列出所有仿真曲线，只将不同速度情况下横东向及横北向重力扰动水平分量引起的位置误差漂移率总结如表3-4所示。

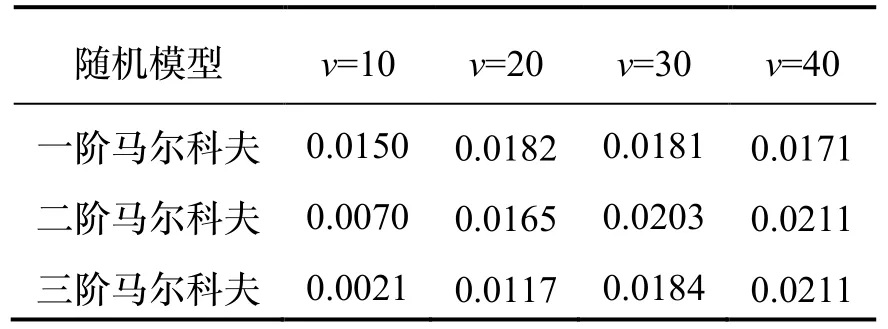
表3 不同速度情况下横东向重力扰动水平分量引起的位置误差漂移率（单位：nmile/h）Tab.3 Drift rate of position error caused by the eastward projection of gravity disturbance in the transversal geographic coordinate system under different velocities

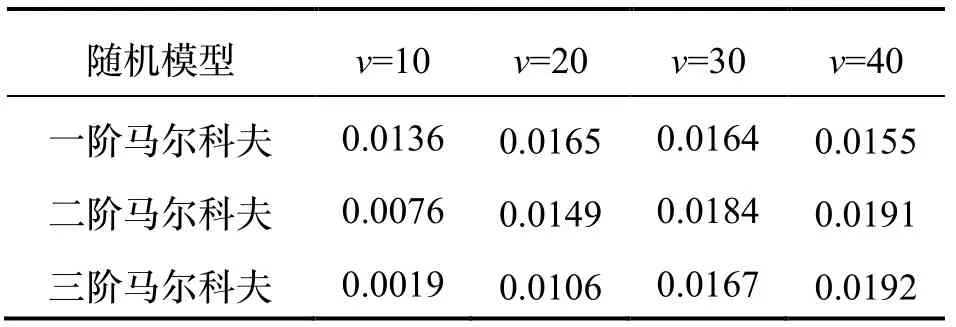
表4 不同速度情况下横北向重力扰动水平分量引起的位置误差漂移率（单位：nmile/h）Tab.4 Drift rate of position error caused by the northward projection of gravity disturbance in the transversal geographic coordinate system under different velocities

由上述分析可以看出，与将重力扰动等效为确定性常值不同的是，无论将重力扰动水平分量假设为几阶马尔科夫过程，其引起的横坐标系下惯导系统位置误差都呈线性振荡增长。需要注意的是，不同阶数马尔科夫模型引起的位置误差漂移率也不同。通过对表3-4中数据分析可见，对于船舰这类低速运载体而言，在利用三阶马尔科夫过程描述重力扰动水平分量的情况下，位置误差受载体速度变化影响较为明显，特别是对于长航时航行情况。对于横坐标系下惯导系统速度误差，重力扰动水平分量同样会引起其呈线性振荡增长。由于篇幅限制，相关推导过程不再赘述。

重力扰动水平分量引起的位置误差和速度误差无疑会降低极区横坐标系下捷联惯性导航系统的性能，因此有必要对重力扰动水平分量进行补偿。

3 重力扰动补偿及仿真实验

利用EIGEN-6C4地球重力场球谐模型计算获得重力矢量网格信息，进一步利用矢量网格数据进行插值计算，得到重力扰动信息，并将其补偿到横坐标系下捷联惯性导航系统解算过程中，算法简单易实施，解算效率高，是工程实践中较为实用的一种补偿方法[6]。本文利用三次样条数据插值方法对由EIGEN-6C4重力场球谐模型获得的分辨率为5'5'×的重力扰动数据进行插值，将其分辨率提高到1'1'×，再利用分辨率为1'1'×的重力扰动数据对横坐标系捷联惯性导航系统进行补偿。经度120 °E~125 °E，纬度65 °N~90 °N极区范围内横东向重力扰动数据和横北向重力扰动数据经过插值后，如图7所示。

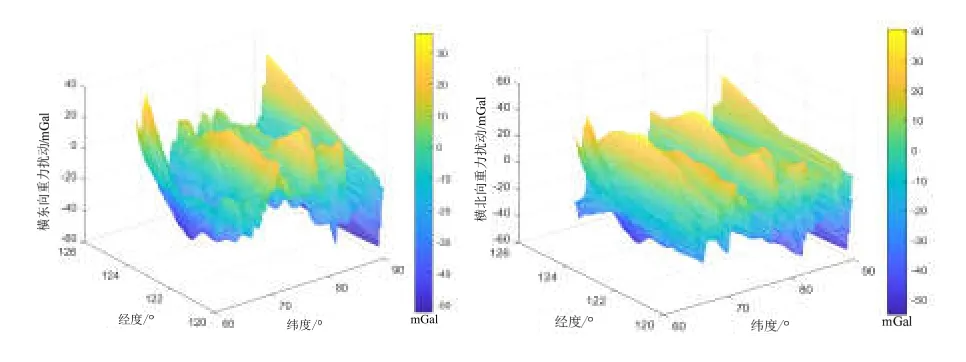
图7 插值后的横东向与横北向重力扰动分量Fig.7 The eastward and northward projection of gravity disturbance in the transversal geographic coordinate system after interpolation

为验证横坐标系捷联惯导系统重力扰动补偿有效性，利用插值后的重力扰动数据进行重力扰动补偿仿真实验验证。仿真条件设置如下：载体以5 m/s的首尾向航速从初始位置120 E°，65 N°沿经线圈匀速航行。加速度计常值零偏为10-6g，陀螺仪常值漂移为0.001 °/h，忽略加速度计和陀螺仪随机误差，仿真时间为120 h。仿真结果如图8-11所示。

图8 重力扰动补偿前后速度误差对比Fig.8 Comparison of speed error before and after gravity disturbance compensation

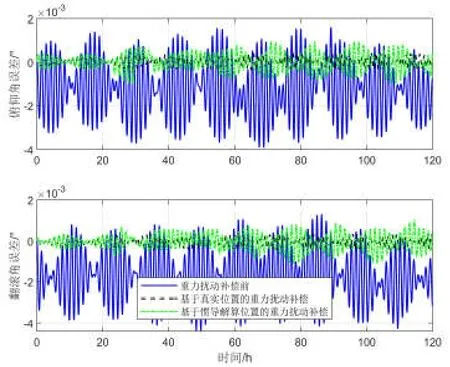
图9 重力扰动补偿前后水平姿态角误差对比Fig.9 Comparison of pitch error and roll error before and after gravity disturbance compensation

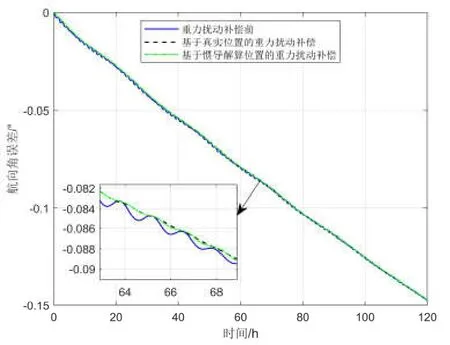
图10 重力扰动补偿前后航向角误差对比Fig.10 Comparison of heading error before and after gravity disturbance compensation

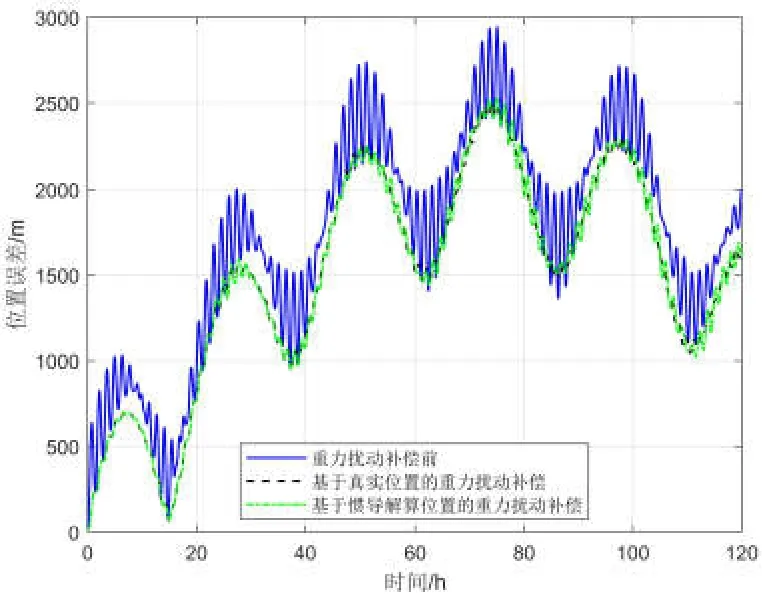
图11 重力扰动补偿前后位置误差对比Fig.11 Comparison of position error before and after gravity disturbance compensation

由仿真结果可以看出，基于2190阶EIGEN-6C4地球重力场球谐模型产生的重力扰动数据经过插值后，可以利用其对横坐标系惯导系统进行有效补偿。经过重力扰动补偿以后，系统速度误差、水平姿态角误差、航向角误差以及位置误差中的振荡性误差都有明显减小。值得注意的是，如果以真实位置信息作为索引值获得重力扰动数据，其补偿精度明显高于基于惯导解算位置信息的重力扰动补偿精度。基于真实位置信息进行重力扰动补偿之后，系统速度误差减小78.3%，水平姿态角误差减小83.2%，位置误差减小3%；基于惯导解算位置信息进行重力扰动补偿之后，系统速度误差减小67%，水平姿态角误差减小68%，位置误差减小2.5%。因此，可以看出惯性导航系统精度也会影响重力扰动补偿效果。同时，基于以上仿真分析可以看出对于极区高精度惯性导航系统来说，重力扰动补偿必不可少。