一种地磁/惯性深度融合导航方法

高 东，朱明慧，韩 鹏

（1.中国科学院国家空间科学中心，北京 100190；2.中国科学院大学，北京 101407）

目前，各国的航天器的主要导航手段为全球导航卫星系统（Global Navigation Satellite System,GNSS），全球导航卫星系统是一种半自主导航系统，特别是近期欧洲Galileo系统的大面积故障，使各军事大国意识到了全球卫星定位系统的不可靠性，甚至在强对抗条件下会被干扰甚至被摧毁。为此，世界军事大国开始研究不依赖GNSS的自主导航技术，使其主航天器在极端条件自主确定自身位置，能够正常工作。

地磁/惯性组合导航是不依赖GNSS的自主导航方式之一，通过载体自主测量所处地磁场、加速度、角速度等信息而实现载体位置和姿态的确定，不需要与外界进行信息交换，是一种无源导航，具有很强的自主性、隐蔽性和抗干扰性，并没有累积误差存在。

将地磁测量信息用于战略战术导弹导航的研究多是利用地磁测量信息来估计导弹旋转速率，或者对磁强计和惯性单元进行补偿和修正[1-4]。一些公司和学者进行了地磁/惯性融合导航测试试验和半物理仿真试验[5-7]。

为了提高地磁/惯性融合导航的精度，国内外学者主要开展了提高地磁模型精度和改进滤波算法等方面的研究。

地磁模型是地磁/惯性融合导航的基础，提高其精度可以有效提高融合导航的精度。针对地磁模型的缓变特性，建立基于神经网络的地磁模型修正模型，通过扩展卡尔曼滤波实现滤波估计的同时在线对神经网络连接权值进行训练，充分利用神经网路对非线性模型的逼近能力，实现对模型误差的修正[8]。此外，基于卫星所测量的三维地磁测量数据，利用基于递推最小二乘的地磁模型三向解耦重构方法实现对地磁模型的快速重构，将地磁模型重构到最新状态，可以在地磁/惯性融合导航应用时有效提高地磁模型的精度[9]。

改进融合滤波算法或使用更先进的滤波方法是另外一种提高地磁/惯性融合导航精度的有效途径。利用广义卡尔曼滤波和无迹卡尔曼滤波算法，可以较好地提高观测方程截断误差的精度[10,11]。将模糊自适应强跟踪滤波算法应用于地磁/惯性融合导航，可以在一定程度上解决融合导航精度下降甚至发散的问题[12]。利用混合校正的卡尔曼滤波器，并引入状态反馈，可以得到导航信息的最优估计[13,14]。

在地磁/惯性融合导航中，地磁场测量野值会导致导航的稳定性下降，甚至发散，基于新息正交性自适应滤波方法可以有效剔除测量野值，提高导航的稳定性[15]。此外，将神经网络技术引入到融合导航中，构造基于新息正交性质的神经网络辅助CKF容错滤波算法，也可以有效避免测量野值对导航稳定性的影响[16]。

将先进滤波方法应用于地磁/惯性融合导航会造成导航计算量增大，难以适应高动态飞行器的导航频率要求，为此将贝叶斯估计引入地磁辅助惯性导航算法中，核心思想为将估计区域网格化,将位置估计转化为概率估计，可在一定程度上提高导航计算效率[17]。

从国内外发展现状来看，学者大多采用先进滤波方式、更多的量测方式开展地磁/惯性融合导航研究，取得了一定成果。本文在前人的研究基础上，对地磁导航、惯性导航的优势和劣势进行分析，充分融合两种导航方法的优点，提出了具备东向速度间接估计的地磁/惯性深度融合导航方法，为高精度地磁/惯性融合导航方式提供一种新的研究思路。

1 地磁/惯性融合导航

地磁导航是利用三轴磁强计测量载体附近的地磁场的三分量，并与载体上的地磁模型的输出值进行比对，并通过导航滤波算法确定出载体的位置信息。从理论上讲，任何一点的地磁场信息与近地空间中的位置一一对应，换言之，地磁场是自然界的天然路标，这是地磁导航的理论基础[18]。本文研究选用国际地磁参考模型（IGRF），选择截断水平为max=13n的IGRF模型，根据弹道数据所在的日期，选择对应的IGRF-13模型。

地磁/惯性深度融合导航系统分为捷联惯导子系统、地磁导航子系统和滤波器子系统。各个子系统之间的联系如下：捷联惯导子系统为地磁导航系统提供其需要的位置和姿态估计信息；地磁导航子系统为滤波器子系统提供量测量；滤波子系统将位置、速度和姿态误差估计量反馈给捷联惯导子系统。如图1所示。

1.1 系统状态方程

本文以在东北天（ENU）地理坐标系下的某弹道作为地磁/惯性融合导航的背景，在ENU坐标系下建立捷联惯导的误差传播方程如下：

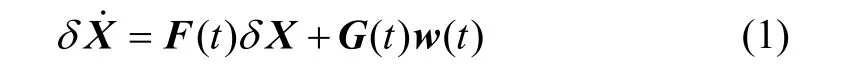
系统的状态方程就是捷联惯导的误差传播方程，其中状态量Xδ的表达式为：

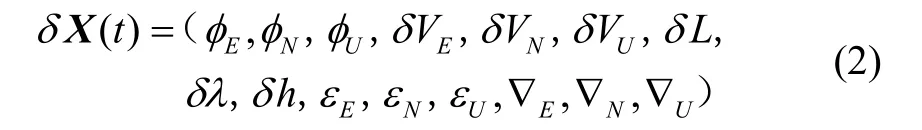
上述表达式中各量的含义依次为：三维姿态角、三维速度、三维位置、三维陀螺漂移和三维加速度计误差。状态方程的具体公式详见文献[19]。

1.2 系统观测方程

地球主磁场起源于地球的内部，其标量磁位U的拉普拉斯方程的解可以通过分离变量法求出，得到其球谐函数的表达式为：

系统的观测方程是基于地磁模型的表达式推导而来，系统的观测方程的形式为：

式中，v(t)为观测噪声，它是由磁强计测量误差与外界环境变化引起的误差的叠加；为地磁矢量观测值。

从系统的状态方程来看，系统的状态量(,,)L hλ在地理ENU坐标系（L为地理纬度，λ为地理经度，h为地理高度），而磁场的三分量在地心NEC坐标系，所以磁场的三分量与状态量(,,)L hλ的关系为：

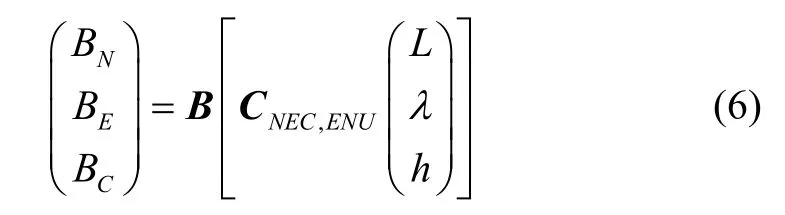
综合以上推导过程，地磁观测矢量与状态量之间的完整关系为：

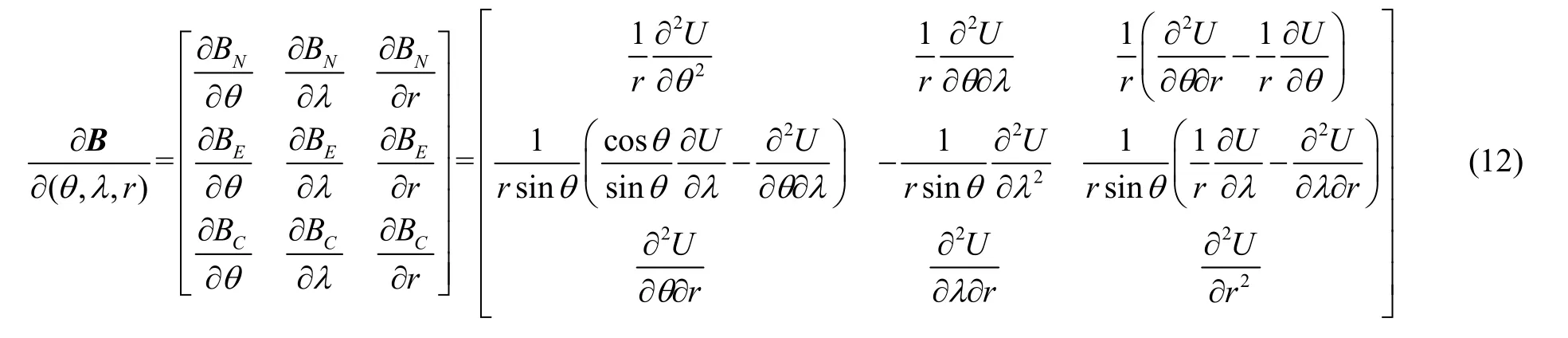
2 地磁/惯性导航特点分析

2.1 地磁导航特点分析

在地磁/惯性融合导航中，观测量为地磁场的三维矢量，为了分析地磁导航的特点，需要对地磁场在北东地三个方向上的特性进行剖析。对50 km~200 km高度的地磁场三分量的梯度信息进行统计，如表1所示。

从表1可以看出，地磁场三分量矢量在高度方向梯度最大，东向梯度最小，北向方向的梯度值与高度方向的梯度值均大于东向方向。在导航新息测量中，观测量在单位位置上的变化越明显，量测能力越高。所以从地磁场的梯度特征来看，地磁导航在高度方向上确定能力最强，而在东向方向（对应地理经度确定）上的位置确定能力最弱。

表1 地磁场三分量梯度统计表Tab.1 Statistical table of three component gradient of geomagnetic field

2.2 惯性导航特点分析

本文基于捷联惯导的误差传播方程对捷联惯导的特点进行分析。

惯性导航的误差传播方程中的位置误差传播方程如式(19)所示。

纬度、经度两个通道是与其他通道的参量相关，具有一定的漂移约束能力。从误差传播方程来分析，捷联惯性导航在高度通道相比其他两个通道的测量信息更易漂移。所以捷联惯导的高度通道相比其他两个通道更需要其他导航方式进行辅助校正。

2.3 地磁/惯性融合导航仿真与分析

从地磁导航、惯性导航的特点来看，地磁导航与惯性导航具有非常好的互补融合性，表现为：地磁导航在高度方向具有高精度位置确定的优势，而在经度、纬度确定方面由于地磁场的量测梯度低而处于劣势；惯性导航在经度、纬度两个通道由于存在耦合信息具有较好的稳定性，而在高度通道没有其他通道的信息约束而容易漂移。地磁与惯性进行融合可以利用地磁导航在高度方向位置确定的优势来弥补惯性导航在高度通道易发散的劣势，实现两者的优势互补。

为了验证地磁/惯性融合的导航的上述特性，对地磁/惯性融合导航进行仿真，参数设置如下：

捷联惯导部分参数：

1）陀螺常值零偏：0.01 °/h

3）加速度常值零偏：10 μg

地磁测量部分参数：

1）磁强计测量误差：30 nT/轴

2）磁强计测量频率：100 Hz

弹道数据：某弹道数据，数据长度15 min。

导航仿真结果如图2-5所示。

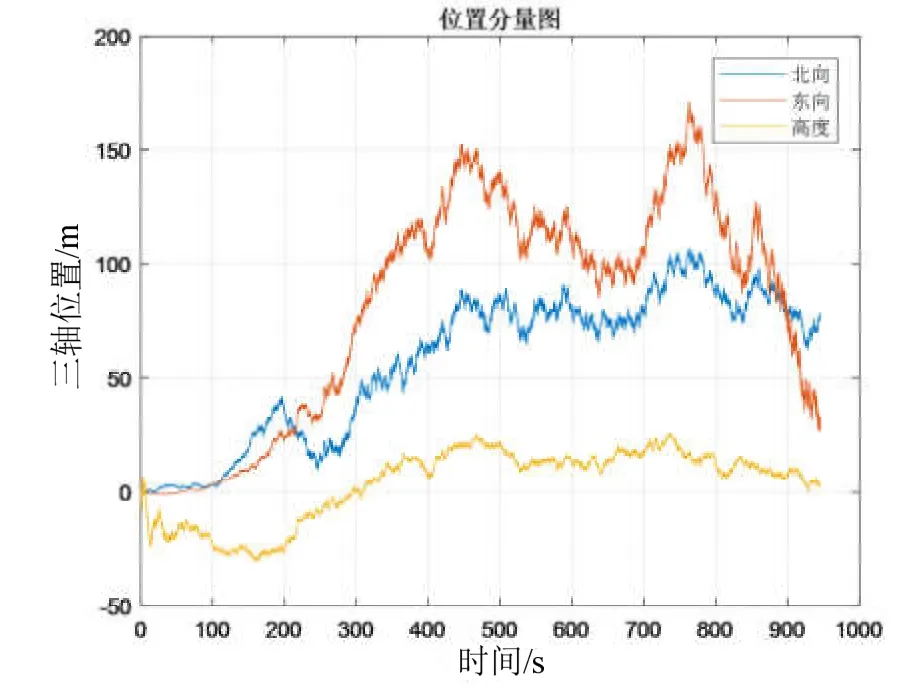
图2 地磁/惯性融合导航位置误差图Fig.2 Position error of geomagnetic/Inertial fusion navigation

从图2可以看出，地磁/惯性融合导航在东向方向的位置误差最大，高度方向上的位置误差最小。在地磁/惯性融合导航中，导航最终的误差由地磁导航的精度决定，图2所示的仿真结果表明：由于地磁场在东向方向的磁梯度很小，地磁导航在经度确定方面的精度较差。为了进一步说明地磁导航的特点，利用导航过程中各状态参量的协方差来阐述各状态量的滤波收敛情况，图3-5为导航仿真过程中的各状态量的协方差图。

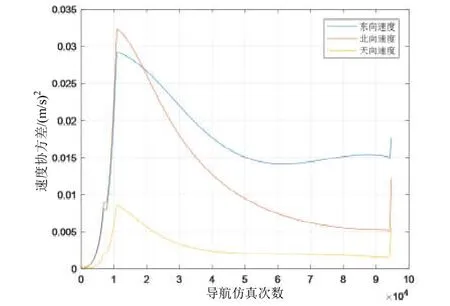
图3 地磁/惯性融合导航速度协方差Fig.3 Velocity covariance of geomagnetic/Inertial fusion navigation

图4 地磁/惯性融合导航经纬度协方差Fig.4 Longitude and latitude covariance of geomagnetic/Inertial fusion navigation

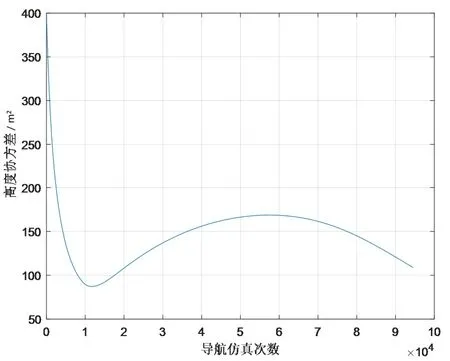
图5 地磁/惯性融合导航高度协方差Fig.5 Height covariance of geomagnetic/Inertial fusion navigation

从地磁/惯性融合导航过程中的位置、速度协方差图可以看出：三维速度、纬度和高度的协方差均能够收敛，而在经度方面，其协方差没有收敛稳定。由于在本文研究中用于导航仿真的背景弹道数据只有15分钟，若弹道时间更长，经度的协方差可能会收敛，但是在15分钟的仿真时间内没有收敛，说明地磁场在东向方向的量测能力小的劣势确实会导致地磁/惯性融合导航对地理经度的确定精度较低。

3 东向速度间接估计的地磁/惯性深度融合导航方法

从传统地磁/惯性融合导航方法的仿真结果看出，融合导航对高度和纬度的确定精度较高，而对地理经度的确定精度较低。为此，需要通过地磁与惯性深度融合的方法来屏蔽地磁导航地理经度确定低的劣势。

首先，通过对惯性导航的位置误差传播方程（式(19)）进行分析，从惯导测量的角度来看，惯导的经度误差与纬度、东向速度和高度直接相关，如式(21)所示：

从地磁/惯性融合导航的结果来看，估计状态量中的速度、高度和纬度信息均稳定收敛，所以可以通过地磁测量所确定的纬度、东向速度和高度来间接估计地理经度信息。

其次，从卡尔曼滤波状态量的最优估计公式：

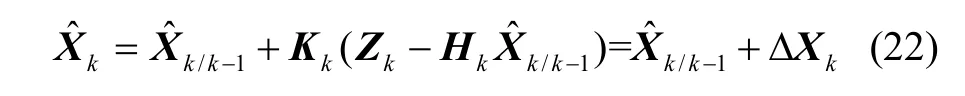
来看，当前状态的最优估计是上一时刻状态的最优估计与当前测量值的加权线性组合。在地磁/惯性融合导航中，惯性导航为基础与核心，地磁导航作为惯导误差的修正，为此可以充分融合惯导、地磁导航的优势部分，即充分利用地磁在高度、纬度方向上的位置确定的优势，同时采用惯导在东向位置确定的优势。

而在地磁/惯性融合导航中，地磁测量作为滤波中的新息，三个方向的新息的修正程度不同，东向方向（地理经度方向）的修正能力最弱。为此，在地理经度的确定过程中，采用式(21)中的经度误差传播方程作为已有地磁观测量之外的新的观测信息，再次融合到地磁/惯性融合导航中，新的地磁/惯性深度融合导航原理图如图6所示。

图6 地磁/惯性深度融合导航原理图Fig.6 Geomagnetic/Inertial deep fusion navigation system

最后，鉴于式(21)的状态量的含义，将由此式间接估计的地理经度误差的变化信息（速度变化信息）代入至惯导误差传播方程中的东向速度方向，在东向速度方程增加一个速度观测新息(相比式(18))，这样系统状态的修正量变为：

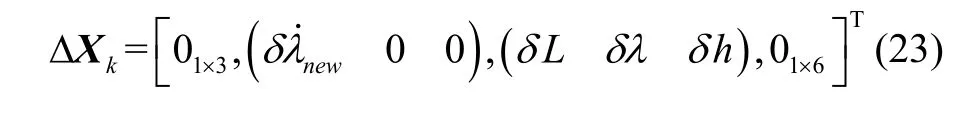
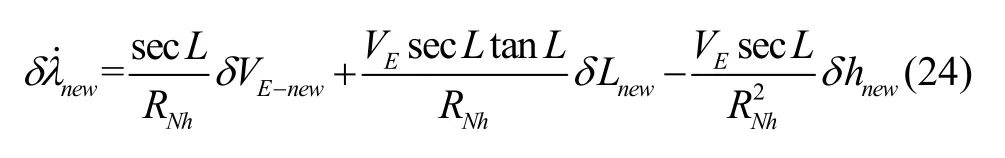
这样，相比传统的地磁/惯性融合导航可以增加一维地理纬度方向的速度观测新息，即间接估计东向速度，抑制东向速度的发散，将地磁/惯性导航在地理经度确定精度低的劣质屏蔽，形成地磁/惯性深度融合导航方法。

为了验证该方法的有效性，维持原有的仿真参数不变，对地磁/惯性深度融合导航方法进行仿真，从仿真结果中分析地理经度确定精度的变化趋势，深度融合前的导航结果如图2所示，深度融合导航后的结果如图7所示。

图7 深度融合后位置分量误差Fig.7 Position component error after depth fusion navigation

从图2和图7的对比来看，在利用地磁/惯性融合导航所确定的纬度和高度信息来间接估计东向速度信息的方法，有效提升了东向位置的误差，使东向位置误差的大小接近北向位置误差。这样，也可以进一步减小总的位置误差，如图8-9所示。

图8 深入融合前总位置误差Fig.8 Position error before depth fusion navigation

图9 深度融合后总位置误差Fig.9 Position error after depth fusion navigation

从地磁/惯性深度融合导航的仿真结果来看：1）地理经度的确定误差与地理纬度的确定误差相当，2）绝对位置误差从深度融合前的211 m（1 σ）减少至深度融合导航的114.7 m（1 σ），位置确定精度提升45.6%。仿真结果说明所提出的利用地磁/惯性融合导航所确定的纬度和高度来间接估计东向速度误差的方法可以有效吸收地磁、惯性导航方法的优点，将地磁导航在地理经度确定的劣势屏蔽，有效提升融合导航的精度。

从另一角度来看，利用惯导的经度误差传播方程、地磁导航确定的高度和纬度信息重新定义观测新息，可以使地磁/惯性导航中通过测量所确定的新息的特性与惯导的状态更新特性一致，更符合惯导的状态更新规律。

4 结论

本文面向固体火箭不依赖GNSS的自主导航的需求，研究了地磁/惯性深度融合导航技术；首先对地磁导航、惯性导航的优缺点进行了分析，发现地磁导航的优势在于确定高度和纬度信息，而惯性导航的优势在于确定经纬度信息，而在高度确定方面存在较大的漂移，地磁/惯性融合导航可以充分将两种导航方式的优势进行组合，摒弃各自的劣势；在传统地磁/惯性融合导航的基础上，提出了利用惯导的经度误差传播方程、地磁确定的高度和地理纬度信息间接估计东向速度的观测新息的地磁/惯性深度融合导航方法；最后，基于某弹道数据对两种导航方法进行仿真看出，所提出的方法可以有效吸收地磁、惯性导航方法的优点，切实进一步提升地磁/惯性融合导航的精度。