基于角加速度滤波的柔性杆臂补偿方法

丛明宇，丁 鹏，戴志军，程向红

（1.东南大学 仪器科学与工程学院，南京 210096；2.微惯性仪表与先进导航技术教育部重点实验室，南京 210096；3.江西洪都航空工业集团有限责任公司，南昌 330024）

捷联惯性导航系统利用固连在载体上的惯性元件测量信息，在给定初始导航参数的基础上通过积分推算，高频率地输出载体的位姿和速度。精确的初始对准技术是保证其导航精度的关键。而机载传递对准属于动基座初始对准技术中的一个重要分支，借助高精度主惯导系统提供的导航信息，低精度子惯导系统可通过传递对准和滤波融合来实现快速、精确的初始对准以提高导航精度。

主子惯导系统在安装上存在的空间位置差异称之为杆臂。当载机机动存在角运动时，不同于载机中心安装的主惯导，子惯导会敏感到除载机机动加速度之外的比力，因而解算出的速度会存在误差，这种现象即为杆臂效应。同时，飞行器在高速机动情况下，受空气气流、载荷变更、发动机噪声等多种因素的影响，机体会产生时变弹性变形，作用在杆臂上，子惯导会偏离其标称杆臂矢量的位置，从而产生挠曲位移，由此产生了柔性杆臂问题。由于杆臂矢量不再是常值，杆臂效应也变得更加复杂，在速度观测量中简单补偿刚性杆臂速度误差已不能解决该问题。

挠曲变形及其带来的柔性杆臂问题，在分布式时空基准系统[1]、机载导航系统[2]的传递对准问题中广泛存在，针对该问题，诸多学者提出了解决方案[1-9]。李四海等[2]比较了白噪声补偿法和有色噪声补偿法，发现将挠曲变形视为有色噪声并采用量测扩增法设计滤波器可提高对准精度。Geng等[3]考虑速度误差定义改进速度误差微分方程，采用12维对准模型避免挠曲变形和动态失准角的影响。Wang等[4]将巴特沃斯低通滤波器引入到传递对准领域，以尽量消除机翼挠曲和振动对算法的负面影响。

另外一种精度较高应用广泛的方案是成形滤波器法处理挠曲问题[5-7]，在此基础上估计并减小动态杆臂带来的误差：Gao等[5]分析了挠曲所致杆臂变化关系，建立了挠曲和杆臂加速度关系模型，考虑了每个变形角对一杆臂项的耦合，但实际中每个变形角耦合的杆臂项不是一项而是两项；Cao等[6]为更好地补偿动态杆臂和获得精确位置信息，在假设失准角为小角度前提下，建立了变形角和杆臂间的变化模型。Fan等[7]提出相对导航的概念，计算对准过程中不同惯性元件间的实时相对运动，在机翼挠曲变形存在的情况下建立相对导航误差模型。

以上方法均需计算杆臂效应中加速度误差项，而杆臂加速度误差模型中需要使用对应滤波时刻主惯导的角速率及角加速度。实际工程中的数据传输会存在随机延时和数据丢包的情况[8]，对于存在大机动的情况，数十毫秒量级的延时会造成较大数据差异，从而影响柔性杆臂加速度计算的准确性。另一方面，由于没有角加速度测量装置，角加速度要从角速度中提取。如果采用简单的差分方式从角速度中提取，差分放大效应会严重降低杆臂加速度误差模型的构建精度。针对以上问题，本文用子惯导角速率代替主惯导角速率，同时引入跟踪微分器[9]，克服角速率信息的噪声放大效应，获得跟踪角速率信号的微分。

本文综合考虑挠曲变形和动态杆臂问题，针对柔性杆臂问题提出改进的传递对准方案。首先利用几何关系推导挠曲变形角与动态杆臂矢量间的关系，建立柔性杆臂的动态估计与补偿模型；其次利用跟踪微分器改进柔性杆臂效应模型；利用Kalman滤波估计方法估计相关物理量，最后进行仿真验证。

1 量测失准角误差模型

根据文献[10]，推导的传递对准系统误差传播方程，量测失准角模型为：

2 柔性杆臂模型

2.1 挠曲变形模型

机翼弹性变形主要有两种，一种是由于载机机动所产生的低频大幅值结构挠曲，另一种是载机内部振源或阵风等使载机机翼产生高频小幅值振动变形[11]。两种变形一般都可以看作是随机过程。低频的挠曲变形，用二阶或三阶马尔可夫模型（Gauss-Markov）描述，如式(2)所示；高频震颤，能够引起带随机相位的位置和速度误差，单一频率分量可用式(3)表示，但在多个频率分量叠加的实际情况下，一般建模为白噪声。

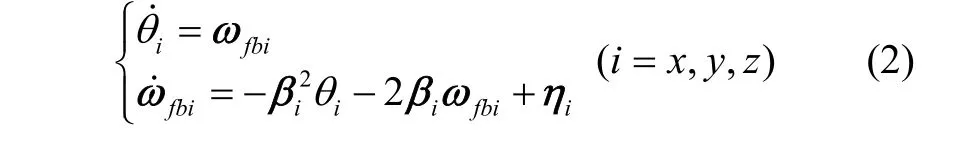
2.2 柔性杆臂模型

文献[11]指出机翼变形可从悬臂梁变形角度考虑，图1为挠曲角影响杆臂变形简化示意图。其中图1(a)为挠曲变形角引起的杆臂矢量变化在主惯导m系下观察的示意图，图1(b)为在挠曲变形角作用下的杆臂矢量y轴方向投影位移示意图。

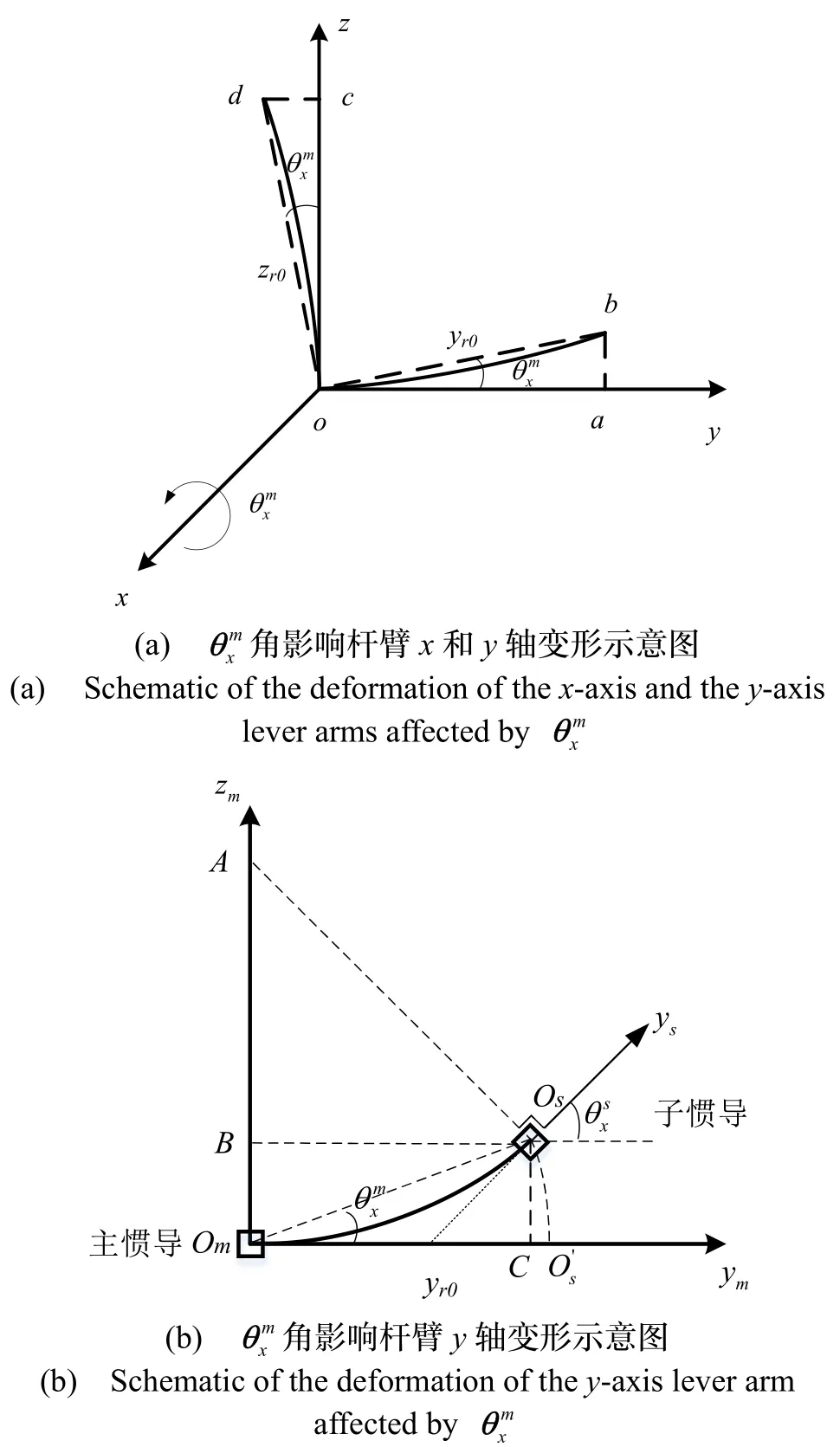
图1 挠曲角影响杆臂变形示意图Fig.1 Lever-arm deformation diagram affected by deflection angle

式(2)-(13)推导了柔性杆臂模型，给出了杆臂变化量与挠曲变形角的关系式，以及杆臂变化的一阶和二阶微分形式。与文献[6]杆臂模型相比，该模型着重区分了挠曲变形角在主子惯导不同坐标系下的观测量。

3 杆臂效应

杆臂效应造成的系统误差主要包括载体角速度与杆臂耦合引起的牵连速度和牵连加速度两项。主惯导和子惯导在空间中的相对地心惯性中心位置分别为Rm、Rs，主惯导和子惯导安装中心不重合，杆臂为r。

由文献[3]和文献[5]推导可知，主子惯导存在的速度关系和加速度关系为：

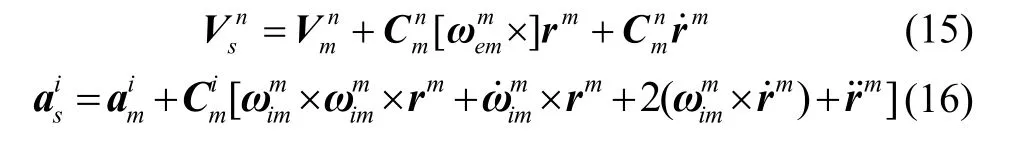
由此可以定义杆臂速度以及杆臂加速度为：

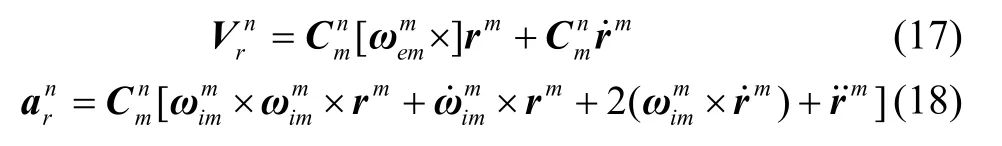
式(17)是导航系下杆臂速度模型，被用来补偿主子惯导在观测速度中的杆臂速度，提高速度观测的精度。在杆臂动态条件下，代入柔性杆臂式(13)，可得柔性杆臂速度：

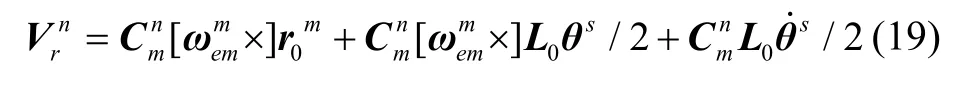
式(18)是导航系下的杆臂加速度模型，被用来补偿惯导系统加速度模型，可被拆解为杆臂矢量初始部分和变化部分造成的杆臂加速度：

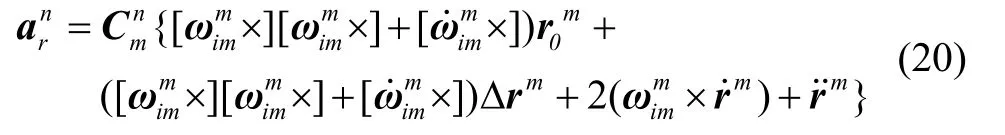
将式(20)代入柔性杆臂式(13)中，得柔性杆臂加速度：

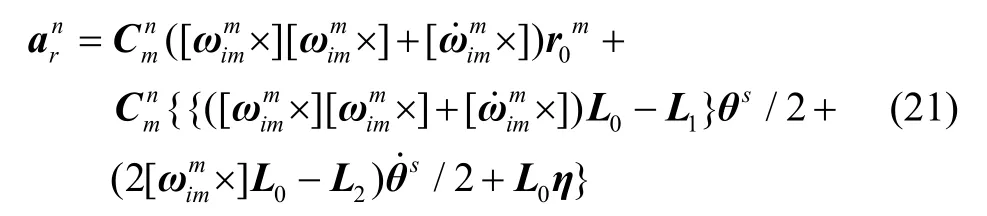
式(21)为柔性杆臂加速度模型。并将该模型拆解开，可定义杆臂加速度为刚性（初始）杆臂加速度部分和杆臂挠曲加速度部分：

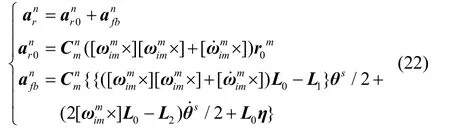
4 基于跟踪微分器的杆臂加速度模型

4.1 跟踪微分器

跟踪微分器（Tracking differentiator,TD）被应用于自动控制系统中，从被噪声污染的信号中合理提取微分信号。对给定信号作用如下微分环节：

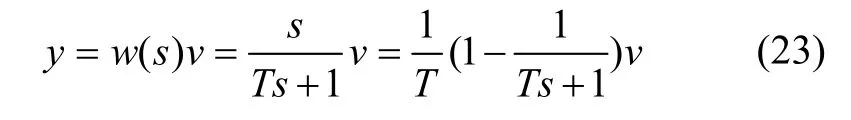
输入信号是v(t)，输出是y(t)。等价框图：

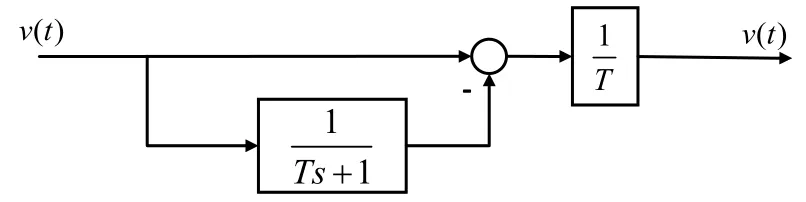
图2 一阶惯性微分环节Fig.2 The first order inertial differential element

等效于经典微分器为：

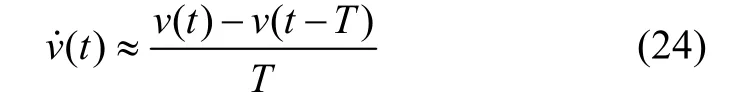
式中v(t-T)为输入信号v(t)的延时信号，时间常数T越小，输出越接近微分的真实值。文献[9]指出，若输入信号被随机噪声污染，式(24)输出信号是输入信号微分结果叠加上放大了1/T倍的噪声信号，从而T越小，噪声放大越严重，完全可以淹没微分信号v̇(t)。这是典型微分环节的噪声放大效应。

为了消除或减弱噪声放大效应，提出二阶近似微分公式：

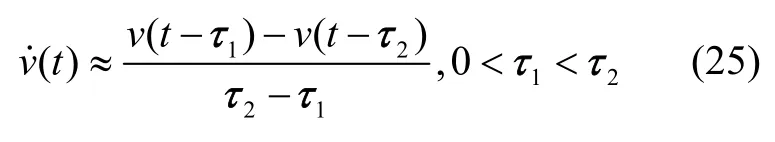
式中v(t-τ1)、v(t-τ2)采用两个惯性环节1/(τ1s+1)和1/(τ2s+1)来获取，可以降低噪声的放大效应，等效框图如图3所示：

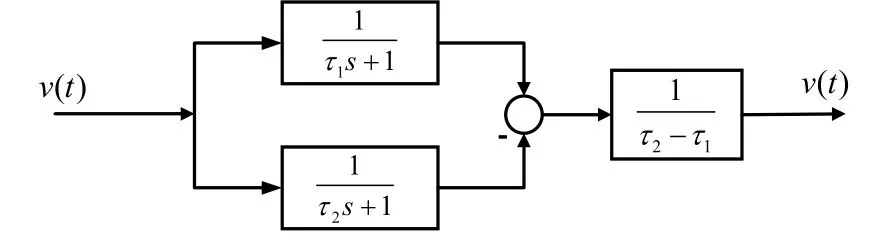
图3 二阶惯性微分环节Fig.3 The second order inertial differential

当时间常数τ1、τ2接近于常数τ，那么上述二阶惯性微分环节等效二阶传递函数为：

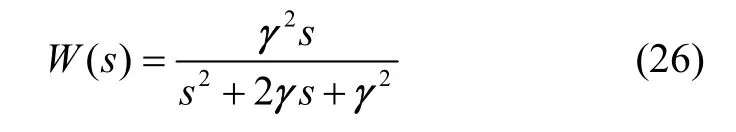
其中，γ=1/τ。本文采用文献[9]中对于γ的选取原则，仿真也验证了该选取原则能使跟踪微分器具有很好的噪声抑制能力。

通过取较小的时间常数，二阶惯性微分环节能很快地跟踪输入信号的动态特性，且能够通过求解微分方程来获取近似的微分信号，因此这个动态结构被称为跟踪微分器。

将传递函数式(26)离散化，得到线性跟踪微分器：

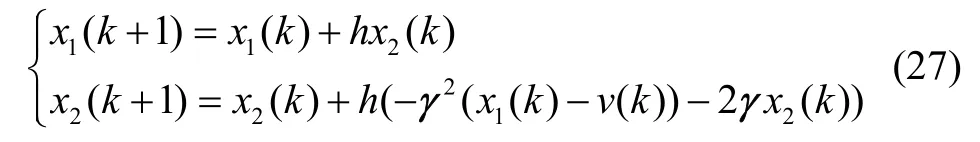
式中v(k)是被跟踪的信号序列，x1(k)是跟踪序列，x2(k)是求解信号微分的结果；参数h是积分步长，一般与信号采样周期一致；参数γ是时间常数的倒数，跟踪的响应速度与γ成正比，γ越大，越能充分地逼近信号v(t)，但是抑制噪声的能力越弱。使用跟踪微分器时，需要合理选择h和γ参数(一般设置hγ＜1)。

4.2 柔性杆臂加速度模型的改进

将4.1节微分跟踪器（TD）应用到角速率的跟踪过程中，可跟踪获得较为理想的角加速度。以捷联惯导系统主子惯导y轴角速率信息为例进行应用说明。仿真中，模拟余弦信号周期为3 s、幅值为25 °/s的理论角速度tWib、主惯导角速度曲线Wibm、受挠曲变形角影响的角速度曲线Wibs，以及对信号微分处理结果。图4(a)展示观察到0~5 s时间段内各个角速率对比曲线，TDx1是跟踪微分器跟踪子惯导角速率的结果；图4(b)展示了主子惯导角速率与理论角速率的差值ΔWibm和ΔWibs，以及运用TD跟踪子惯导角速度的误差曲线ΔTDx1。仿真中的惯性器件误差以及挠曲变形的参数设置在6.1小节中。

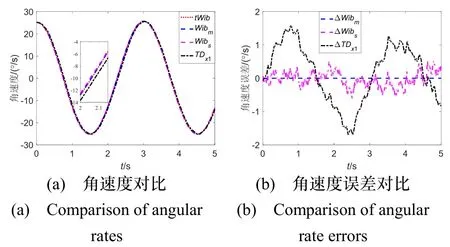
图4 角速度曲线比较Fig.4 Comparison of angular rate curves

工程上常用简单差分得到角加速度，该方法引入较大噪声，应用效果如图5所示。dtWib曲线表示无误差的角加速度曲线，dWibs此处表示用式(24)经典微分器的处理结果（时间常数设为采样周期的两倍，已经具有一定的平滑效果），TDx2表示采用式(27)跟踪微分器的微分求解结果。从图中对比可知，采用TD对带挠曲成分的子惯导角速率进行微分，其结果能减少微分误差至经典微分器1/2~1/3的水平，具有一定的预滤波和平滑的效果。因而，可在柔性杆臂加速度误差模型中使用TD求得的子惯导角加速度结果。

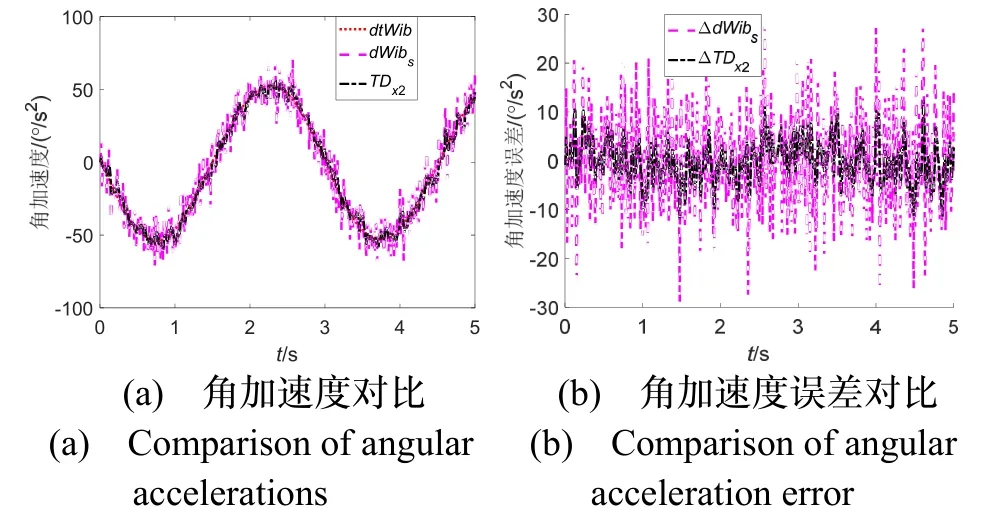
图5 角加速度曲线比较Fig.5 Comparison of angular acceleration curves

综上所述，将柔性杆臂加速度模型(22)改写为：

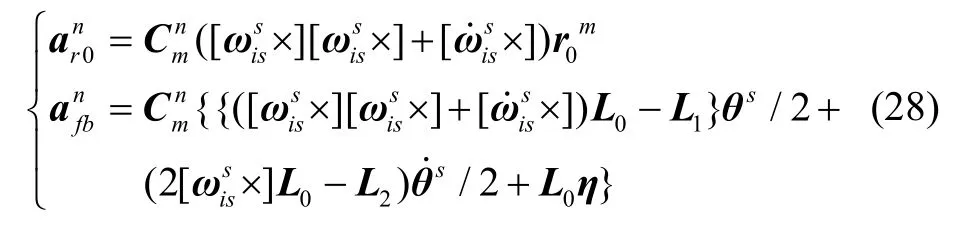
相比模型(22)，式(28)直接使用子惯导角速率和其微分结果作为模型分量，避免了主惯导角速率传输延迟的问题，在传递对准过程本身需要实施较大机动的应用场景下是较为合理的，该改进模型更具工程适用性。

将式(28)模型代入量测失准角系统速度误差方程(1)中，可以得到新的速度误差方程：

5 针对柔性杆臂的传递对准误差模型

针对柔性杆臂推导基于量测失准角的系统误差模型。

5.1 传递对准系统误差模型

选取22维状态量X建立针对柔性杆臂的传递对准系统状态方程：

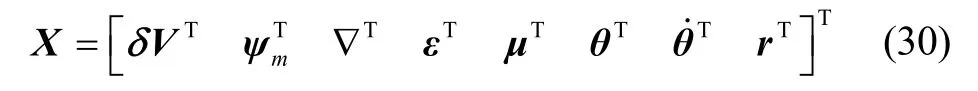
其中δVT和∇T为二维状态量，其余为三维状态量。δV表示速度误差状态量，忽略天向通道的速度误差；ψm表示量测姿态角；μ表示安装误差角；θ表示挠曲变形角；表示挠曲变形角速率；∇表示加速度计测量零偏，忽略天向加表零偏；ε表示陀螺常值漂移；r表示杆臂矢量。

定义s系下安装误差角为μ，μ和θ组成了主子惯导间实际相对姿态角：

将安装误差角、加速度计零偏、陀螺漂移建模为随机常值，则系统误差模型方程可以表达成：

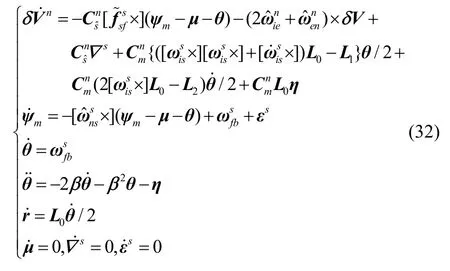
5.2 传递对准观测模型方程

采用“速度+姿态”匹配方式进行针对柔性杆臂情况下的传递对准。

针对柔性杆臂的“速度”匹配方式观测方程为：

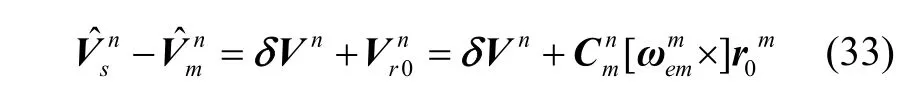
针对柔性杆臂的“姿态”匹配方式观测方程为：

提取式中量测姿态角mψ用于观测。

建立针对柔性杆臂的“速度+姿态”匹配方案观测矩阵。观测量为速度（2维）、量测失准角（3维）：

观测矩阵为：

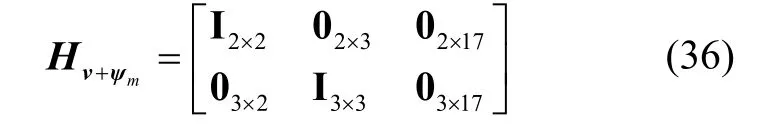
6 仿真实验

设计基于白噪声模型和基于柔性杆臂模型的系统误差模型对比。

白噪声模型建立在量测失准角系统模型的基础上，将挠曲变形带来的杆臂加速度误差项去掉，即式(22)中项去掉，改为在系统的速度误差方程中注入一定强度的白噪声，以此验证柔性杆臂模型优劣。

6.1 仿真设置

如图6所示，搭建了针对柔性杆臂的仿真平台，模拟动态环境，对准效果受挠曲变形角、安装误差角、器件误差等误差源的影响，对对准的性能如对准收敛时间、对准精度进行评估。

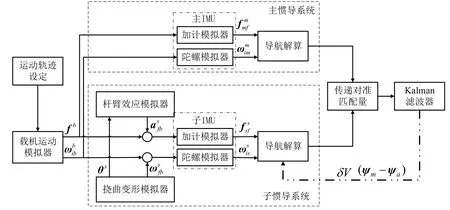
图6 传递对准仿真流程图Fig.6 Flow chart of transfer alignment simulation

主要仿真条件设置如下：

1）仿真的轨迹为北偏西45 °匀速直飞，速度为100 m/s，同时伴随着俯仰机动（幅值/周期为5 °/4 s）和横滚机动（幅值/周期为12 °/3 s）。

2）静态安装误差角绕x/y/z轴为20＇/15＇/16＇。

3）初始杆臂x/y/z方向为10 m/2 m/-1 m。

4）x、y、z轴挠曲变形均方差/相关时间为2 °/4 s、2 °/3 s、2 °/10 s。

6）设置速度量测噪声为0.1 m/s，姿态量测噪声为0.6 '。

7）设置步长h与采样周期相同为5 ms，γ为80 s-1。

6.2 仿真结果与分析

分别用白噪声模型、无柔性杆臂补偿模型和柔性杆臂补偿模型对传递对准各参数状态进行估计，仿真结果如图7所示。

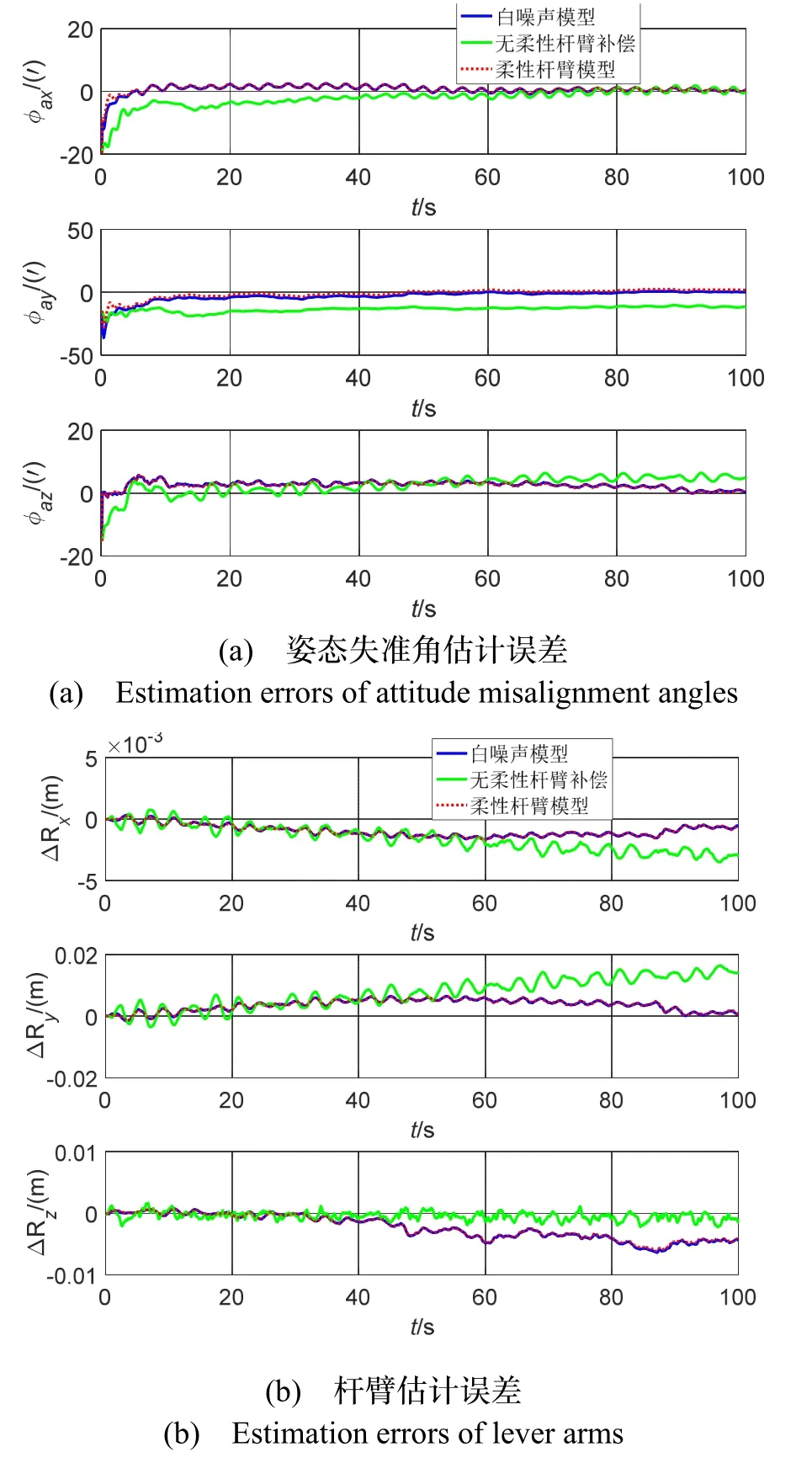
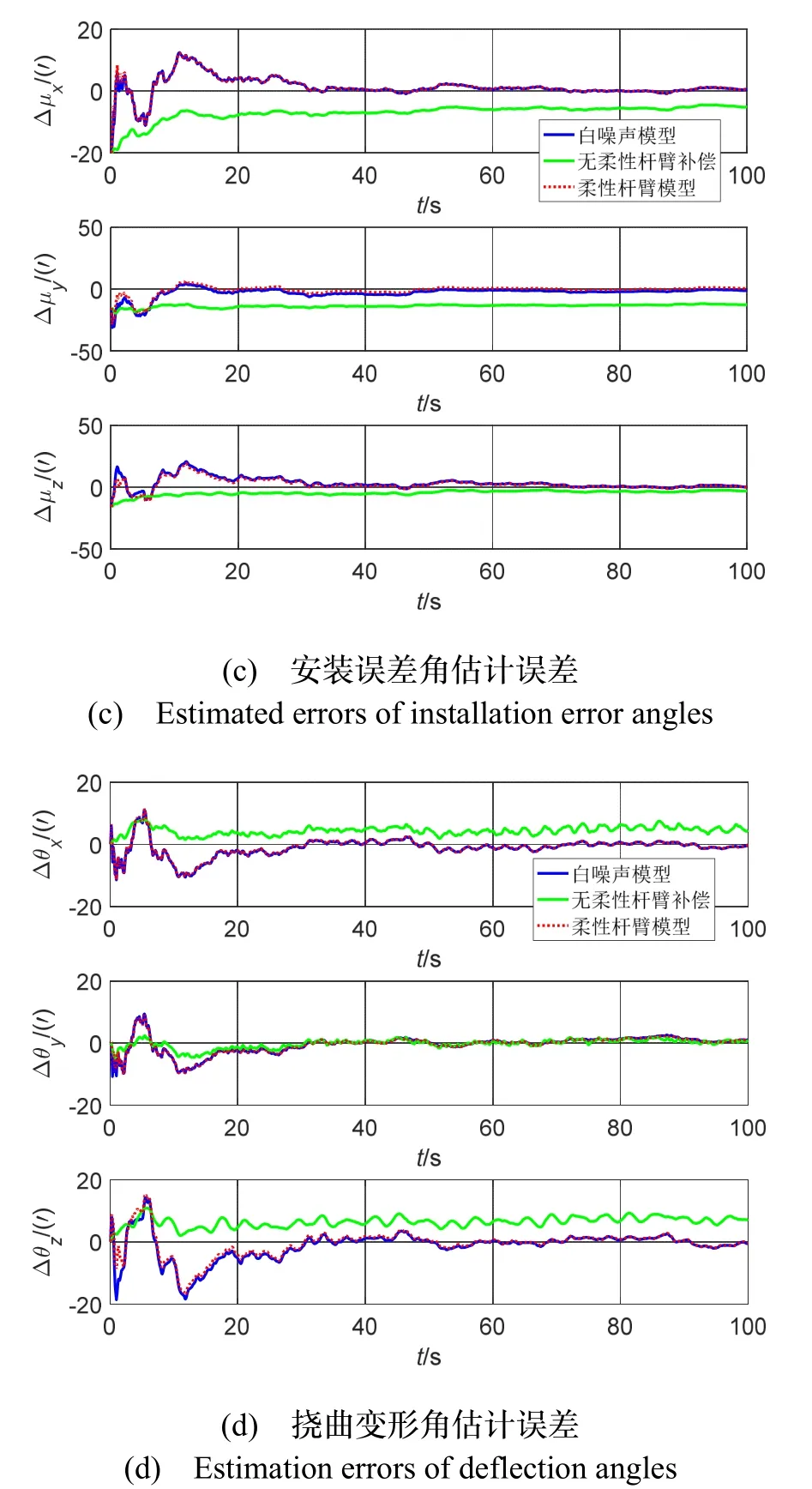
图7 基于白噪声模型和基于柔性杆臂模型的系统误差模型仿真对比Fig.7 Simulation comparison of system error model based on white noise model and flexible arm model

如图7(b)(d)所示，一方面，由于没有改变系统误差模型的姿态误差方程以及杆臂与挠曲变形角的关系，挠曲变形角、杆臂大小的估计情况没有显著区别。另一方面，由图7(a)(c)可知，与注入白噪声的方式相比，柔性杆臂模型应用在速度误差方程中，可有效地改进安装误差角的估计，最终提高量测失准角的估计精度。

为具体说明基于跟踪微分器改进的传递对准柔性杆臂误差补偿方法效果，统计了图7所述仿真中20~100 s的平均绝对误差（Mean Absolute Error,MAE）大小（此时滤波器已收敛），表征基于两种模型的参数估计情况。其中姿态失准角φa表征计算子惯导坐标系与子惯导实际坐标系之间的误差角，该值趋于零表示估计精度高。

从表1可以明显看出，相较于白噪声模型，应用基于跟踪微分器的柔性杆臂模型对x轴的安装误差角和姿态失准角估计精度效果不大，但对y、z轴的安装误差分别提高了48.7%和16.7%，对y、z轴的姿态失准角分别提高14.0%和5.4%，对三轴平均安装误差估计精度提高了22.3%，姿态失准角估计精度提高了4.6%，提高了对准精度。

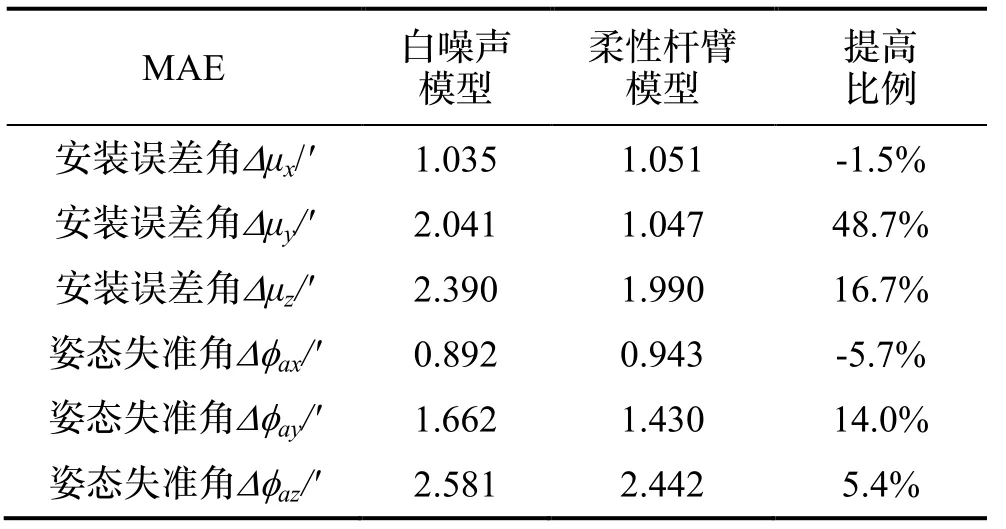
表1 基于白噪声模型或柔性杆臂模型的参数估计（MAE）对比表（20~100 s）Tab.1 Comparison Table of Parameter Estimation (MAE)Based on White Noise Model or Flexible Arm Model (20～100 s)

7 结论

本文将挠曲变形问题和相关的动态杆臂问题综合进行考量，分析机翼挠曲变形对传递对准精度的影响，利用几何关系推导挠曲变形角与动态杆臂矢量间的关系，建立柔性杆臂的动态估计与补偿模型，提出引入跟踪微分器改进柔性杆臂效应误差模型，利用Kalman滤波估计方法估计相关物理量。仿真表明改进的模型相对白噪声模型有效提高了安装误差角和姿态失准角的估计精度，提高了子惯导初始对准精度。

本文的主要创新点在于利用跟踪微分器求取角加速度，本质上是利用跟踪微分器低时延的低通滤波特性，克服简单差分带来的噪声放大效应。在自动控制领域还有许多其他快速跟踪微分器的形式，能给出品质较好的微分信号，值得在惯性/卫星导航等需要跟踪信号微分的领域探索应用。