利用步行惯性导航的室内定位融合算法研究

柏思琪+梁文海+秦爽

摘 要： 步行惯性导航是一种用于无基础设施室内定位中的新技术，但累积误差效应限制了它的使用范围，为解决此问题，提出一种把步行惯性导航与无线测距定位相融合的定位算法，结合前者轨迹连续和后者无累积误差的优点。仿真结果表明，该融合算法在定位的稳定性和精确性方面都表现出良好的性能，验证了该方案的合理性、有效性。

关键词： 室内定位； 惯性导航； 零速度更新； 卡尔曼滤波； 融合算法

中图分类号： TN96?34； TP274 文献标识码： A 文章编号： 1004?373X（2015）0 引 言

室内定位系统应用前景广泛，越来越受到研究学者的重视。考虑精度、成本、功耗、尺寸及复杂性等各方面条件，目前还没有一种普适的室内外无缝定位系统。根据是否需要基础设施，室内定位系统分为有基础设施的定位系统和无基础设施的定位系统[1]。前者在搜救、反恐等场合几乎不适用，后者适用范围较为灵活。全球定位系统（Global Positioning System，GPS）可用在无基础设施定位系统中，在大多数室外环境都可以实现较高精度的定位，但在恶劣的室外环境及室内环境下，需要其他定位系统协同完成定位，如惯性导航[2]。步行惯性导航模块非常适合用于无基础设施室内定位，其优点是体积小、成本低、功耗低，但最大的缺点是有累积误差，其累积误差随位移非线性增长，“零速度”更新（Zero Velocity Update，ZUPT）卡尔曼滤波算法[3] 能将累积误差限制在线性增长范围内，在此基础上，还可利用陀螺仪、电子罗盘、磁力计的测量值协助卡尔曼滤波算法消除惯性导航方向上的累积误差[4]。这些方法都能在一定程度上提高步行惯性导航的准确性，但对较长时间行走还需要其他消除累积误差的方法。例如，另一类有效方法是将惯性导航与其他无累积误差的定位算法相融合。文献[5]介绍了一种将指纹定位与惯性导航相结合的经验算法，对精度的提高有一定效果，但指纹定位算法对数据库的建立和维护要求较高，不适用于无基础设施定位。针对上述问题，本文提出一种卡尔曼滤波算法，融合了步行惯性导航和基于测距定位信息，该算法计算复杂度低、速度快、融合效果好。仿真结果表明，该算法的定位轨迹平滑、误差小且无累积误差，对无基础设施室内定位系统实现具有很好的参考意义和应用价值。

1 步行惯性导航

智能手机通常内置了惯性测量装置（Inertial Measurement Unit，IMU），包括加速度传感器和陀螺仪传感器等，市场上也很容易购置到IMU模块。理论上，目标的移动距离可通过IMU采集到的加速度通过两次积分得到，但对于消费级IMU模块，仅考虑牛顿运动方程时，人行走的位置误差的标准差正比于时间的三次方，仅仅几秒时间的行走就会导致几米的误差。人在行走时总会有停止状态，理论上停止状态的速度应该为零，但实际上依靠IMU几乎无法测到速度为零的情况。ZUPT惯性导航算法的基本思想是采用一些经验检测方法检测停止状态[6?7]，将该状态的速度人为置零，这种方法在减小惯性导航累积误差上取得了很好的效果，例如，瑞典KTH大学设计的开源惯性导航系统OpenShoe[8]基于安装于人脚踝的ADIS16367 IMU（包括加速度和陀螺仪）和Atmel AVR32UC3C微控器，能很好地实现零速度检测。

OpenShoe方案把人为置零时速度的误差作为卡尔曼滤波的测量值[mk，]称为伪测量值，用[vk]表示[k]时刻的速度，则[mk=0-vk，]而不是直接用速度作为测量值，采用伪测量值的原因是IMU并不能真正测量到零速度。系统在“零速度”时刻用卡尔曼滤波跟踪方向矩阵[Cnb，k]以及各状态向量：位置的误差[δrk，]速度的误差[δvk，]导航坐标系下姿态的误差[δφk，]加速度传感器的测量误差[δak]和陀螺仪传感器的测量误差[δωk，]每个状态量均由三个坐标轴上的分量构成。完整的状态向量为[δxk=[δrk，δvk，δφk，δak，δωk]T]。用每次滤波的输出状态[δrk，][δvk，][δφk]更新导航状态位置[rk，]速度[vk]和姿态[φk，]用输出状态[δak]和[δωk]更新加速度和角速度的测量值[ak]和[ωk]。算法处理后的位置误差的标准差与行走距离基本是线性的，但依然存在累积误差。因此，本文目的是如何消除步行惯性导航引起的累积误差。

2 基于测距的定位算法

如果能够事先通过基于测距的定位算法得到一个粗糙的位置，就能够利用它来消除累积误差。基于测距的定位方案有ZigBee定位、WiFi定位、扩频频谱信号（Chirp Spread Spectrum，CSS）定位和超宽带定位等，其中ZigBee定位和WiFi定位测量的是接收信号强度（Received Signal Strength，RSS），无基础设施定位一般选用干扰较小的CSS或UWB定位，测量信息是到达时间（Time of Arrival，ToA）。这些定位方案可采用的定位算法也有很多，如三角测量定位算法、最小二乘定位算法、最大似然估计定位算法等。这些算法中各有优缺点，但它们的共同缺点是：受信道不稳定因素的影响，定位结果有跳动现象，跳动的程度由信道环境和算法的稳健性共同决定。例如，Kwang Hyun Lee等提出一种基于CSS的卡尔曼滤波定位系统[9]，其测距精度比ZigBee有明显提高，但仍然有接近2 m左右的跳动。

为了减小无线测距定位结果的跳动，增加定位结果的稳定性，可以把基于测距定位的结果与惯性导航相融合。本文不详细介绍测距定位算法本身，只利用算法输出的位置结果进行融合。

3 融合定位算法

如前所述，惯性导航可产生连续的轨迹，但会伴随位移和方向两方面的累积误差，因此考虑通过测距定位算法来校正。融合算法的主要思想是逐步将惯性导航的结果拉向测距定位附近，以消除其累积误差，如图1所示，图中三角形为起点，实曲线为真实运动轨迹，虚线为惯性导航结果，圆圈为测距定位结果。

图1 融合算法原理示意图

将惯性导航系统与测距定位系统视为一个新的导航定位系统。导航系统的状态仍然为[rk，][vk]和[φk，]滤波状态中[δrk，][δvk]修改为[rk，][vk，]其他状态保持不变。位置的测量值可由测距定位系统得到，而速度的测量值仍然通过“零速度”检测得到，注意，两个分系统的采样频率可能会不同，卡尔曼滤波在有测量值时进行，所以新系统的测量值有三种取值：

[mk=[pk，0]T，有位置输出且为“零速度”时pTk，仅有位置输出但不为“零速度”时0T，”仅为“零速度”但无位置输出时] （1）

式中：[pTk]代表测距定位系统的位置测量值；[0T]代表“零速度”。

新系统的滤波状态为[xkk=xk=[rk，vk，δφk，δak，δωk]T，]状态转移方程表示为：

[xkk-1=Fkxk-1k-1+wk-1] （2）

式中：[xkk-1]为预测状态；[xk-1k-1]为[k-1]时刻滤波器的输出状态；[wk-1]是过程噪声，其协方差矩阵为[Qk=E（wkwTk）]。 转移矩阵为[4]：

[Fk=IΔt?I0000I-Δt?S（a′kn）Δt?Cnb，kk-1000I0Δt?Cnb，kk-1000I00000I] （3）

式中：[S（a′kn）]为与加速度值相关的对称阵，其取值可参见文献[4]。新系统的测量矩阵为：

[H=I00000I000，有位置输出且为“零速度”时[0I000]，仅有位置输出但不为“零速度”时[I0000]，仅为“零速度”但无位置输出时] （4）

新系统的测量方程为：

[zk=Hxkk+nk] （5）

状态更新方程与经典卡尔曼滤波一致：

[xkk=xkk-1+Kk?[mk-Hxkk-1]] （6）

其中卡尔曼增益[Kk]也按照经典卡尔曼公式更新：

[Kk=Pkk-1HT（HPkk-1HT-Rk）-1] （7）

[Pkk-1]为预测状态协方差矩阵，根据[k-1]时刻的测量来计算：

[Pkk-1=Fk-1Pk-1k-1FTk-1+Qk-1] （8）

[Pk-1k-1]的计算方程为：

[Pkk=（I-KkH）Pkk-1（I-KkH）T+Rk] （9）

用每次滤波的输出状态[rk，][vk，][δφk]更新导航状态位置[rk，]速度[vk]和姿态[φk，]用输出状态[δak]和[δωk]更新加速度和角速度的测量值[ak]和[ωk]。

融合算法的计算复杂度由惯性导航方程与卡尔曼滤波方程共同决定，前者为牛顿运动方程，复杂度低，所以总的计算复杂度由卡尔曼滤波部分决定。卡尔曼滤波的算法复杂度为：

[3n3+3mn2+2m2n+mn+A+B]

式中：[n]表示状态向量维数，本文算法即为15；[m]表示测量向量维数，本文算法为6或3；[A]为状态一步预测的乘法次数，本文算法为225；[B]为测量一步预测的乘法次数，本文算法为30。这样，程序运行一次总共所需执行的乘法次数大约为15 000次，选择合适的DSP器件需要运行的时间仅为毫秒级。

4 算法仿真

人行走时的加速度和角加速度值可以通过程序模拟产生，产生的方法见文献[10]。本文加速度和陀螺仪的仿真数据来自公开数据库http：//www.openshoe.org/。仿真数据分别是直线行走300步和沿固定轨道走10圈两种情况，人的行走速度为1.2 m/s，采样频率为100 Hz，加速度和陀螺仪数据的噪声假设为高斯白噪声，标准差分别为0.012 m/s2和0.008 7 rad/s，它们还分别有1个[y]轴上的偏差0.1 m/s2和0.05 rad/s，偏差的噪声也为高斯白噪声，标准差分别为0.04 m/s2和0.012 rad/s。假设测距定位系统的输出频率为IMU模块的[15，]20 Hz，其测量噪声为高斯白噪声，在3个轴上的标准差都为1 m。两种情况下融合算法与Openshoe惯性导航算法定位的轨迹比较图如图2，图3所示。

图2 直线行走300步仿真结果

图3 固定轨道走10圈仿真结果

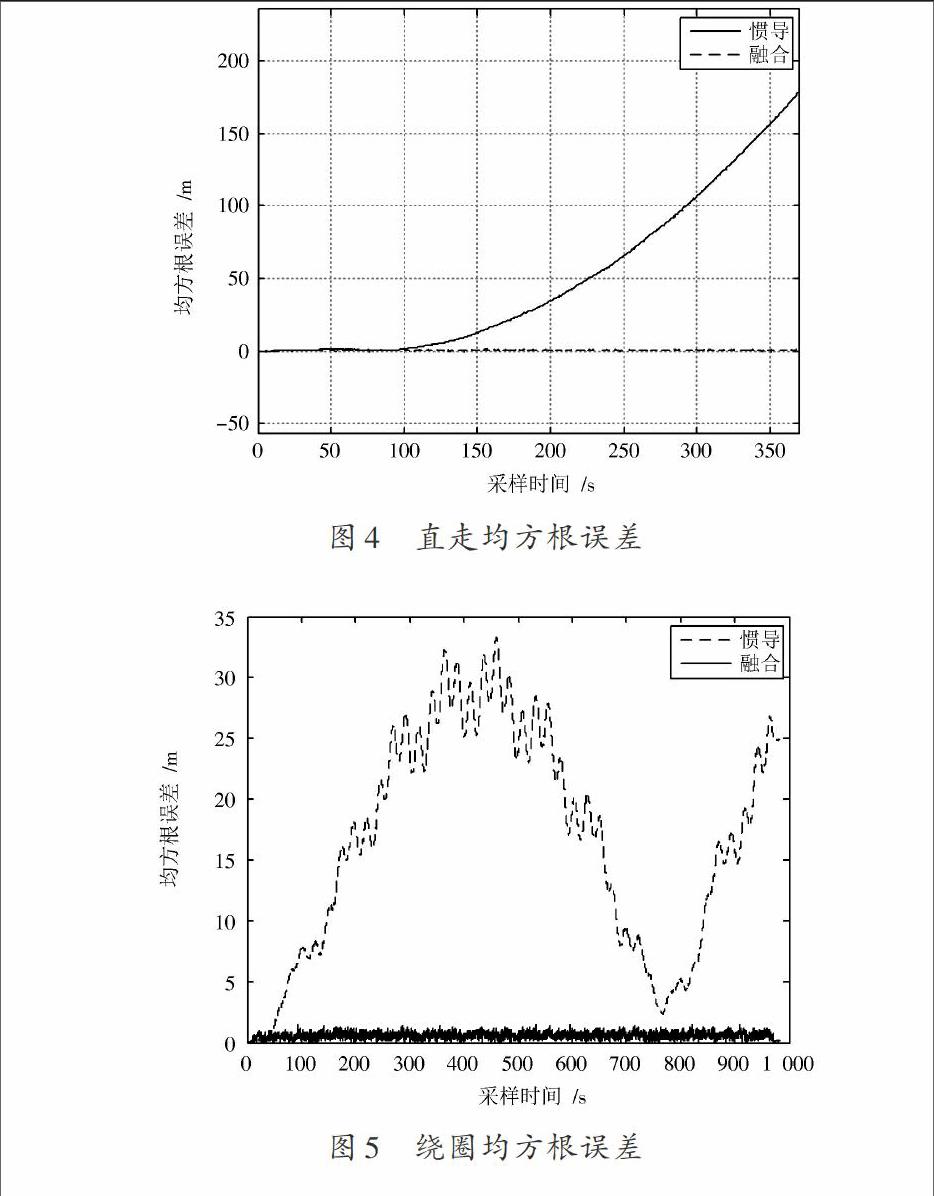
从图2可以看出，由于传感器的偏差和噪声的存在，惯性导航的轨迹大约在[y]轴方向100 m处就开始偏离真实行走轨迹，并且偏离程度随着行走距离变远而越来越大，而融合定位轨迹始终在真实轨迹附近，且比基于测距的定位结果更稳健、更准确。对于沿固定轨道绕圈的仿真结果也同样如此，如图3所示，惯性导航与真实轨迹越来越不重合，而融合定位轨迹的结果始终在真实轨迹附近，同样比基于测距的定位结果更稳健、准确。造成惯性导航偏离真实轨迹的主要原因是传感器（加速度和陀螺仪）的噪声和偏差对时间的两次积分，其中偏差对惯性导航的影响更为明显，在无偏差的情况下，融合算法对惯性导航结果的改善程度比有偏差的情况小，但仍有提高，限于篇幅在此不给出仿真结果。沿直线行走是惯性导航的最坏情况，均方根误差随着行走距离的增大不断增加，如图4所示。当绕圈时，由于加速度存在一个正向的偏差，惯性导航的速度比人的真实行走速度快，均方根误差总体呈现一个增大的趋势，当惯性导航结果超过人的真实位置半圈时，均方根误差增加到最大，随后呈现减小趋势，直到超过真实位置一圈时，误差降到最小，然后按照同样的趋势增大，如图5所示。无论是走直线还是绕圈，融合算法的均方误差始终最小，进一步说明融合算法有更好的性能。

图4 直走均方根误差

图5 绕圈均方根误差

5 结 语

无基础设施室内定位技术在救援、反恐等特殊场合有重要意义，步行惯性导航是可用于无基础设施室内定位的重要技术之一，因此，研究如何消除惯性导航的累积误差非常具有实际价值。本文提出的融合定位算法在稳定性和精确性两方面都表现出较为优越的性能。下一步的工作是搭建实测嵌入式定位平台以进一步验证算法的实用性，在实测定位平台基础上融合更多定位方法，如GPS、UWB、计算机视觉等，以实现更灵活、更精确的室内外无缝定位。

参考文献

[1] NOH Y， YAMAGUCHI H， LEE U， et al. CLIPS： infrastructure?free collaborative indoor positioning scheme for time?critical team operations [C]// 2013 IEEE International Conference on Pervasive Computing and Communications. San Diego： IEEE， 2013： 172?178.

[2] LEE S， BYOUNGGEUN K， HOON K， et al. Inertial sensor?based indoor pedestrian localization with minimum 802.15.4a configuration [J]. IEEE Transactions on Industrial Informatics， 2011， 7（3）： 455?466.

[3] FOXLIN E. Pedestrian tracking with shoe?mounted inertial sensors [J]. IEEE Computer Graphics and Applications， 2005， 25（6）： 38?46.

[4] JIMENEZ A， SECO F， PRIETO J， et al. Indoor pedestrian navigation using an INS/EKF framework for yaw drift reduction and a foot?mounted IMU [C]// 2010 IEEE Workshop on Positioning， Navigation and Communication. Dresden， Germany： IEEE， 2010： 11?12.

[5] 周亮，付永涛，李广军.无线定位与惯性导航结合的室内定位系统设计[J].电子技术应用，2014，40（4）：73?76.

[6] ZAMPELLA F J， JIMENEZ A R， SECO F， et al. Simulation of foot?mounted IMU signals for the evaluation of PDR algorithms [C]// 2011 IEEE International Conference on Indoor Positioning and Indoor Navigation. Guimaraes： IEEE， 2011： 1?7.

[7] SKOG I， HANDEL P， NILSSON J O， et al. Zero?velocity detection?an algorithm evaluation [J]. IEEE Transactions on Biomedical Engineering， 2010， 57（11）： 2657?2666.

[8] NILSSON J O， SKOG I， HANDEL P， et al. Foot?mounted INS for everybody?an open?source embedded implementation [C]// 2012 IEEE International Conference on Position Location and Navigation Symposium. Myrtle Beach： IEEE， 2012： 140?145.

[9] LEE K H， CHO S H. CSS based localization system using Kalman filter for multi?cell environment [C]// IEEE International Conference on Advanced Technologies for Communications. Hanoi： IEEE， 2008： 293?296.

[10] ZAMPELLA F J， JIMENEZ A R， SECO F， et al. Simulation of foot?mounted IMU signals for the evaluation of PDR algorithms [C]// 2011 IEEE International Conference on Indoor Positioning and Indoor Navigation. Guimaraes： IEEE， 2011： 1?7.