动态地球磁层的时空剖分编码*

王慈枫 胡晓彦 邹自明 李云龙 白 曦

1(中国科学院国家空间科学中心 北京 100190)

2(中国科学院大学 北京 100049)

3(国家空间科学数据中心 北京 100190)

0 引言

地球磁层是大多数航天器运行的区域，也是太阳等外源因素影响地球空间的关键区域，具有重要的研究与应用价值。随着数字化、智能化、网络化传感器技术等现代探测技术的快速发展与大规模应用，对地球磁层的观测越发全面、立体、精细。当前，空间物理对地磁资料的组织主要包括两种方式。第一种是基于数据的语义特征，例如时间、载荷等，构建一系列资源间的层级关系，从而实现资料组织和索引[1]。然而，不同卫星、不同台站在数据预处理时会建立各自独立的组织和索引方式，因此这种方式不利于数据的检索、整合、共享和分发。第二种是基于坐标系的重组和索引，空间物理领域结合学科特征提出了一系列专用坐标系。这些坐标系大致可以分为三类，即地心坐标系、日心坐标系和局地坐标系[2]。这种方式进行数据资料组织的基本思想是对现有资料的时空信息在特定应用场景下进行坐标转换等处理，然后利用文件系统或传统的关系型数据模型进行重组和存储。选择适当的坐标系可以使资料排列更加合理、计算结果更容易理解。然而，这类模型在不同的应用场景下需要选择不同的坐标系，且这些坐标系的定义有明显的学科特征，因此不利于多尺度、跨学科领域的数据组织和计算研究。

在研究空天地一体化地球大数据模型时，提出了地球剖分格网的概念，即对地球球体进行不断细分，得到多层级的剖分格网，并设计编码方案实现格网编码，从而便于格网在计算机中的表达和计算，构建统一、多分辨率、可计算的时空框架。有研究将剖分、编码的思想应用到了日地空间物理领域的相关研究，提出了一系列涵盖近地空间部分区域的剖分模型，如GeoSOT-3D 立体剖分模型[3]、球体退化八叉树剖分格网模型（Sphere Degenerated Octree Grid，SDOG）[4]、层级三角网时空模型（Hierarchical Triangular Mesh –Sphere & Time，HTM-ST）模型[5]等。从这些模型的研究对象出发考虑，对其空间范围的描述可遵循以地球为中心向外延展至地表、近地空间各圈层乃至外部空间的基本思路。因此，针对规则（椭）球面、（椭）球体提出的剖分方案可以对研究对象的空间位型进行有效拟合。但是，地球磁层是受地球磁场、太阳风等多源因素综合影响形成的一个非规则化的动态物理空间，因此以（椭）球面、（椭）球体为基础的空间剖分模型及其编码方案难以在所有应用场景下对磁层空间进行有效表达。地球磁层时空剖分模型基于粒子运动的漂移壳并结合磁场物理要素，实现了一定时空范围内的磁层区域剖分。该模型得到的格网形变稳定且可以反映磁场要素的物理特征，适合作为地球磁层区域的通用剖分模型。

格网编码是剖分得到的各时空格网在计算机中的数字化表达。在剖分模型的基础上实现剖分格网的编码是构建时空基础框架至关重要的内容，支撑着数据的快速索引及高效计算。目前，编码方案大致可以划分为层次编码、填充曲线编码和整数坐标编码三类[6]。层次编码是在给定初始层次单元的码元后，根据剖分格网之间的层次结构，对其子单元用后缀（前缀）码元表示，适用于父子单元边界重合、层次关系明确的剖分模型。例如，HTM-ST 模型[5]基于层次编码方案设计了模型对应的编码，完成了卫星轨道面的可计算时空框架构建。填充曲线编码是一种通过递归覆盖指定区域的一维曲线。SDOG 模型基于退化Morton 曲线编码实现了数字虚拟球体的构建[4]；圈层格网模型基于Hilbert 填充曲线设计了模型对应的编码方案，实现了地球圈层空间基础框架的构建[7]。整数坐标编码是最简单直接的格网编码方案，在格网空间中定义m个坐标轴，则格网的m维整数坐标即为其对应的编码。填充曲线编码和整数坐标编码可以很好地反映格网在指定域中的分布关系，使格网邻域计算更高效；而层次编码则可以更便捷、快速地计算格网之间的父子关系。这些传统的编码方案适用于规则的、时空关系较为明确的各类格网表达，与地理坐标系等各类传统坐标系之间的转换较为简单，可以支持基于这些编码的格网间时空关系计算。但是，由于磁层空间位型的特殊性，地球磁层时空剖分模型得到的剖分格网往往是不规则的，且格网之间的时空关系较为复杂，用一维编码难以实现完整表达。

本文对地球磁层时空剖分模型格网的基本特征进行分析。基于剖分格网的时空特性，设计编码方案对其进行数字化表达，从而为粒子输运过程、辐射带动态变化等研究场景提供一种新的时空框架。最后，设计实验分析编码效率，验证编码方案的高效性。在此基础上，设计基础相邻关系计算效率对比实验，验证采用不同编码方案进行高效时空计算的可行性，为后续复杂计算与科学分析奠定基础。

1 地球磁层时空剖分模型

1.1 漂移壳的构造

基于漂移壳实现地球磁层动态剖分，首先要根据磁场特征，实现漂移壳的构造。漂移壳参数L为描述漂移壳的重要参数之一。McIlwain[8]将L定义为磁镜点磁场强度Bm和积分不变量I之间的关系，并提出在偶极磁场条件下，L的几何含义为磁力线与磁赤道面交点到地心的距离与地球半径的比值。一般而言，L≤3 的范围内，地球磁场可以近似为偶极磁场，故而可以将磁层空间分为L≤3 的偶极磁场区域和L ＞3的非偶极磁场区域[9]。

漂移壳由一系列磁力线构成，偶极磁场区域的磁力线方程可以表示为[10]其中，θ和φ分 别为磁纬和磁经，r为径向距离（其单位为地球半径Re），C为常数。此时，可以直接利用上述方程构造漂移壳。偶极磁场区域L={1.5,2,2.5}的各漂移壳如图1 所示。

图1 偶极磁场区域L ={1.5,2,2.5}的各漂移壳构造Fig. 1 Construction of the drift shells with L={1.5,2,2.5}in the dipole field

非偶极磁场区域以Galperin 提出的L值计算方法为基本思想，漂移壳构造方法如下。

（1）利用式（1）计算L=L0的面，称为参考L面（ReferenceLSurface），该曲面与磁赤道面（Magnetic Equatorial Plane）的交线用ΘF表示为

（2）从ΘF上任意一起点P出发，在IGRF 磁场模型[11]下利用龙格库塔–梅森法[12]，向地磁北极方向追踪磁力线至地球表面，交点记为Foot Point North。

（3）从Foot Point North 出发，在IGRF+Tsyganenko96（T96）磁场模型[11,13]下向地磁南极方向追踪磁力线至地球表面，若该磁力线不能在预先设置的有限步骤内闭合，则认为该磁力线为开放磁力线，对应暴露于行星际太阳风的区域，不在本文模型中进行剖分。

（4）针对ΘF上所有选取的起点执行步骤（2）（3），形成的所有磁力线构成的曲面即为非偶极磁场区域漂移壳。

上述方法对其中一条磁力线的构造过程如图2所示。使用外源场模型T96 时所需的太阳风参数、地磁指数等从OMNI 数据库获取.

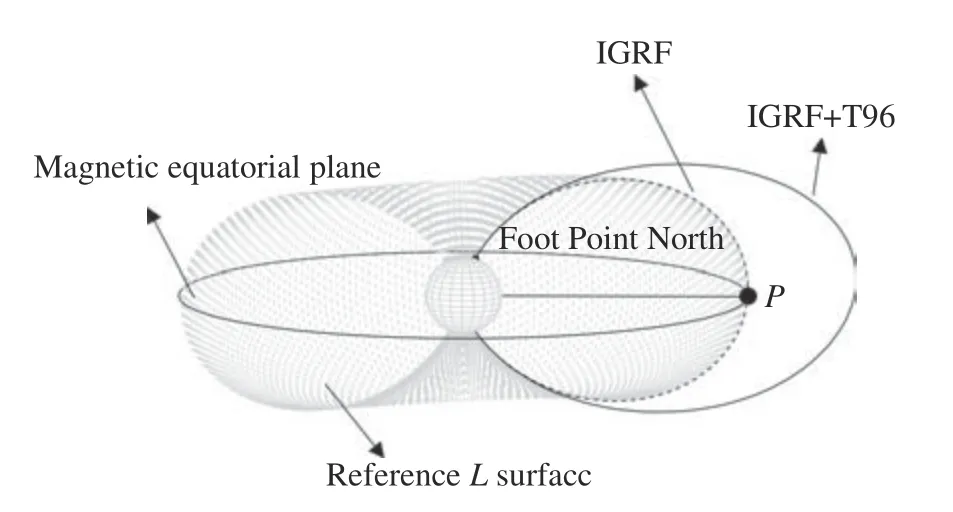
图2 基于Galperin 计算方法的磁力线构造方案Fig. 2 Construction of a field line of the drift shell based on the calculation of Galperin L

非偶极磁场区域漂移壳的构造结果与时间密切相关，本文统一用yyyyddd表 示时间，其中ddd为年积日。t=2015169非 偶极磁场区域L={6.5,7,7.5}的各漂移壳构造结果如图3 所示。

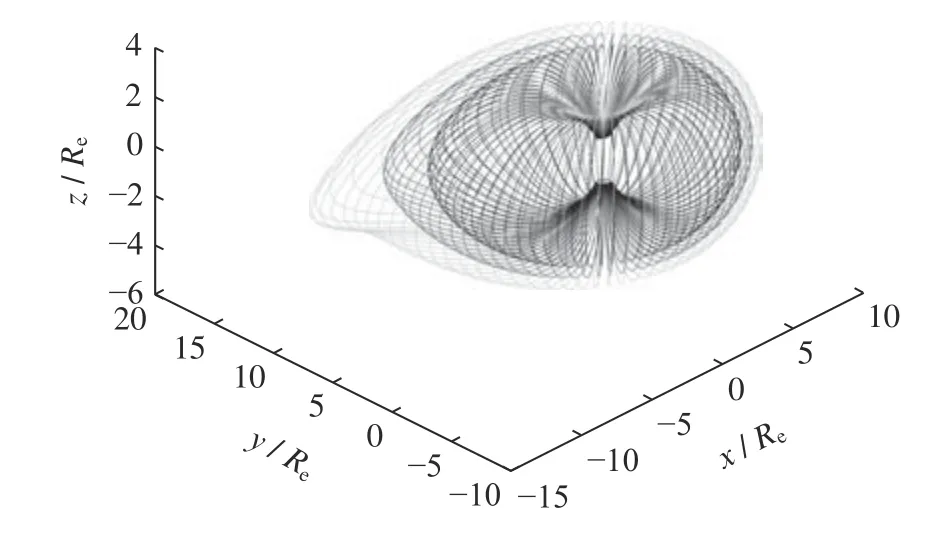
图 3 非偶极磁场区域 t =2015169， L={6.5,7,7.5}的各漂移壳构造Fig. 3 Construction of the drift shells witht=2015169 and L ={6.5,7,7.5} in the non-dipole field

1.2 剖分模型

以上述漂移壳构造方法为基础，提出一种地球磁层时空剖分模型。剖分后得到一系列具有时空内在联系的时空格网。为方便论述，对地球磁层时空格网相关术语定义如下。

时间间隔 Δt(N)： 剖分N次时两个时间格网之间的时间差。

径距ΔL： 两个漂移壳的参数值L之差。

纬距 Δθ(N)： 同一时间下，空间剖分N次时两个空间格网之间最大纬线与最小纬线的纬度差。

磁力线距ΔφF(N)： 同一时间下，空间剖分N次时空间格网左下顶点与右下顶点的经度差。

经距 Δφ(Nφ)： 在漂移壳上进行Nφ次等经度剖分，两条经线之间的经度差。

在空间剖分方面，该模型首先在径向上选择一系列不同的L值，将磁层空间离散为一组漂移壳。针对不同场景，可选择等径距离散或根据粒子的分布特征在径向上进行适应性离散，随后对每个漂移壳曲面进行剖分。漂移壳由磁力线段构成，沿磁力线对漂移壳进行剖分可以使剖分格网与磁场条件相关联，以支持基于磁场的时空关系计算。沿磁纬方向采用等纬度间隔剖分，使计算量最小。

在非偶极磁场条件下，漂移壳的构造与时间密切

由剖分模型可知，偶极磁场区域的磁力线与磁经线保持一致，即在同一条磁力线上，所有点的磁经度相同。因此，有N=Nφ且

（1） 磁力线距不确定性。格网间的磁力线距ΔφF(N)是 磁场决定的，不同格网之间的ΔφF(N)不同。

（2） 层次关系不确定性。在进行下一层级的剖分时，是对Θeq进行递归二等分，得到起点后构造磁力线，因此剖分层级的格网之间的层次关系难以确定。

（3） 时空关系复杂性。在不同时间格网下，漂移壳的空间位型不同。因此不同时间下，同一L值对应的漂移壳之间的时空关系极为复杂。本文暂不讨论时空关系计算，只在同一时间的条件下讨论基础空间关系计算。

2 时空剖分模型编码方案

为了构建支持高效检索与计算的时空框架，需要对剖分得到的各时空格网进行编码表达，以便于计算机对其存储和处理。编码过程中用到的符号标记定义如下：N表示该编码对应的格网剖分层级，上标表示在某一维度的编码，下标表示编码进制，如(idθ(N))2表 示剖分N次时，格网纬度对应的二进制编码。在下文出现的二进制计算中，乘法和加法都是按位计算。

图4 L =1.5的漂移壳剖分Fig. 4 Subdivision of the drift shell with L=1.5

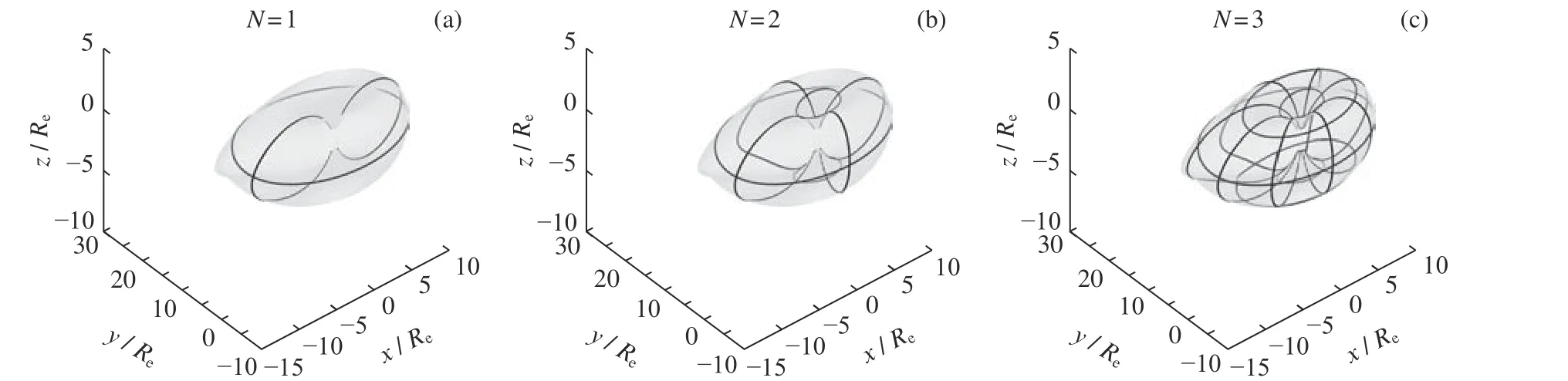
图5 非偶极磁场区域L =7.5， t =2015169漂移壳剖分Fig. 5 Subdivision of the drift shell with L =7.5,t=2015169

利用一个5 位二进制编码(idL)2表达格网所在的漂移壳，从L=1.1向外进行顺序编码，即

每个时空格网的编码由其所在的漂移壳顺序编码和该格网在漂移壳上的时空位置编码串联构成，即

其中，⊕表示编码串联。

2.1 Morton 编码

基于Morton 曲线对剖分模型得到的时空格网进行编码，基本思想为分别在磁纬线（θ）、磁力线（F）、和时间段（t）三个维度上进行顺序编码，记为(idθ(N))10，(idF(N))10，(idt(N))10，再耦合得到对应的时空Morton 编码。

在偶极磁场区域，具体编码步骤如下。

步骤1 分别计算三个维度的十进制顺序编码，有

其中， (idST(N))2的 编码位数为 ( 3N)，其他二进制编码的位数为N。

步骤3 与漂移壳顺序编码串联得到完整编码(id(N))2。例如，T0=2014005，对于一个坐标为(t,L,θ,φ)=(2015169,1.5,0,0)的时空格网，令剖分次 数N=2 时， ΔT=273 d，则 有 (idL)2=00000，(idt(2))10=2， (idθ(2))10=2， (idF(2))10=0，耦 合得(idST(2))2=110000，最终计算得到该格网的(id(2))2=00000110000。

非偶极磁场区域的编码方式与偶极磁场区域类似。但是，对于同一条磁力线上的点可能处于不同磁经度，因此(idF(N))10的计算方法需进行修正。通过计算每条磁力线与磁赤道面（θ=0）的交点经度，再按照交点经度大小对磁力线进行排序得到顺序编码(idF(N))10。 然后将 (idF(N))10代入步骤2 和3，得到非偶极磁场区域Morton 编码(id(2))2。

2.2 整数坐标编码

整数坐标编码是最简单直接的编码方案，其基本思想是在空间中定义m个坐标轴，将剖分格网按照其沿着坐标轴前进的步长进行编码。偶极磁场区域的整数坐标编码方案步骤如下。

步骤1 根据输入的时空坐标 (t,L0,θ,φ)分别计算其在磁纬（θ）、磁经（φ）、时间（t）三个维度上的整数坐标，有

2.3 漂移壳剖分格网编码方案

偶极磁场区域磁力线均匀对称， 有(idF(N))10=(idφ(N))10。因此，任意一种编码(id(N))2都可以较为完整地反映格网的时空信息及其之间的时空关系。但是在非偶极磁场区域，Morton 编码缺乏(idφ(N))10的 信息，即在θ／=0的纬线上，(id(N))2无法直接反映格网的空间左右相邻关系。而整数坐编码则缺少(idF(N))10的信息，因此无法反映两个空间格网是否在一条磁力线上，较难计算空间上下相邻关系。针对非偶极磁场区域，本文结合Morton 编码和整数坐标编码，设计三种能完整表达格网时空信息的漂移壳剖分格网时空编码（Drift Shell Grids Coding, DSGC），方案如下。

方案1

其 中： (idF(N))2的 编 码 位 数 为N； (idt(N))2，(idθ(N))2及 (idφ(N))2的 编 码 位 数 为 max(N,Nφ)。则(idS1T(N))2的 编码位数为3 ×max(N,Nφ)。最后串联漂移壳编码，即

3 实验及结果分析

3.1 编码效率对比

实验使用的软硬件配置列于表1。这里使用了中国科学院国家空间科学中心公共技术服务中心空间科学数据融合计算平台的计算服务。

表1 集群环境Table 1 Cluster environment

图6 非偶极磁场区域漂移壳格网编码Fig. 6 Diagram of the DSGC for the grids in the non-dipole field

在偶极磁场和非偶极磁场两个特征区域内，选择典型的漂移壳对其进行N次剖分，然后对剖分得到的所有时空格网进行编码，计算并分析各编码方案的编码效率（ηc），则有

式中，nc表示总时空格网数，Tc表示编码时间。

偶极磁场区域选择L=1.5，各剖分层级上的编码效率列于表2。非偶极磁场区域选择L={7.5,8}，时间t={2014005,2015169}这4 个漂移壳，计算各剖分层级上的平均编码效率。

从表2 可以看出，随着剖分次数的增多，剖分得到的格网数成倍增加，但编码效率较为稳定，且Morton 曲线编码和整数坐标编码方案的效率相差不大。由表3 可知，漂移壳剖分格网编码方案与传统的Morton 编码方案和整数坐标编码方案的效率相差不大，且当剖分到12 层级时仍能维持在4500 s–1以上。可以认为，本文提出的编码方案编码效率较高。并且对于非偶极磁场区域的格网而言，Morton 编码方案与整数坐标编码方案难以完整表达格网的时空信息，给后续时空关系的计算带来一定的困难。

表2 偶极磁场区域编码效率Table 2 Encoding efficiency in the dipole field

表3 非偶极磁场区域平均编码效率Table 3 Mean encoding efficiency in the non-dipole field

3.2 相邻关系计算效率对比

基于非偶极磁场区域的三类编码，设计基础的空间相邻关系计算，以分析对应编码在进行基础计算时的效率。在同一时间下，一个空间格网的相邻关系包括上邻居（T）、下邻居（B）、左邻居（L）、右邻居（R）、左上邻（TL）、左下邻（BL）、右上邻（TR）、右下邻（BR）。其中，上下左右4 个基础相邻关系的计算列于表4。首先分别计算左邻居的上邻居以及上邻居的左邻居，作为左上邻两个候选者，然后选择距离所求格网较近的候选者作为其左上邻，左下邻、右上邻、右下邻计算方式与此类似。

表4 剖分格网的基础相邻关系Table 4 Basic adjacency of the grids

选择L={1.5,7.5}， 时间t=2015169漂移壳，分别对其进行N=10次剖分，然后在其上随机选取10000 个时空点，分别对其编码并基于三类编码求其对应的8 个邻居，得到一次计算的效率

式中，ns表 示所取样本数，ts表示计算所有样本的8 个邻居的总时间。进行10 次计算后求平均值η-s，得到基础相邻关系计算效率列于表5 和表6。

由表5 可知，偶极磁场区域两种编码方案在计算相邻关系时的效率较高且两者相差不大。因此，对偶极磁场区域可以根据物理存储结构选择合适的编码方案。由表6 可知，一维编码比二维编码在进行基础相邻关系计算时效率低，且计算左右相邻关系时差距尤为明显。可以说明，非偶极磁场区域进行简单的时空计算时，二维编码有一定的优势。

表5 偶极磁场区域格网基础相邻关系计算效率对比Table 5 Efficiency comparison of the basic adjacency of the grids in the dipole field

表6 非偶极磁场区域格网基础相邻关系计算效率对比Table 6 Efficiency comparison of the basic adjacency of the grids in the non-dipole field

4 讨论与结论

分析了地球磁层时空剖分模型得到的非偶极磁场区域剖分格网的基本特征，将其概括为磁力线距不确定性、层次关系不确定性以及时空关系复杂性三点。根据这些特征，本文融合整数坐标编码及Morton 曲线编码的基本思想，提出了三种漂移壳剖分格网编码方案，并设计实验分析了各方案编码效率及基于对应方案的相邻关系计算效率。实验证明，本文提出的编码方案效率较高且可以完整地表达格网之间的时空关系，因此可以较好地支持相邻关系计算。此外，探讨了结合物理场来构建时空框架的方案，试图为后续的科学计算与分析决策提供便利。

但模型仍存在若干局限。第一，本文设计的实验是基于逻辑模型进行的，没有考虑各编码在计算机中的物理层存储设计。几种编码方案虽然编码效率接近，但是在不同的存储模型下，存取速度存在差异，需要根据编码特征设计存储方案。尤其是二维编码(id3(N))2存储到计算机中要保证两个维度的编码都可以唯一地、确定地标记时空格网，因此其对应的存储模型需针对这种特性进行优化设计。第二，在空间适用性方面，完成时空框架构建后要进行数据映射才能够实现该框架在数据组织及高效计算上的应用。而进行数据映射时，对于L值较大的漂移壳（例如，L≥10），可能会引入较大的位置配准误差。因此，基于特定的应用场景提升模型适用性也是未来研究方向之一。

致谢 计算服务支持由国家科技资源共享服务平台–国家空间科学数据中心（https://www.nssdc.ac.cn）提供。