用于深空探测的400 MHz 带宽Chirp 变换谱分析仪的设计与实现*
2022-11-09茹鹏磊刘梦伟宫俊杰朱皓天董晓龙
茹鹏磊 刘梦伟 宫俊杰 王 文 朱皓天 朱 迪 董晓龙
1(中国科学院声学研究所 北京 100190)
2(中国科学院大学 北京 100049)
3(中国科学院国家空间科学中心 北京 100190)
0 引言
在深空探测领域,分子(H2O,CO,HCN,HNC,CH3OH 等)转动谱线大多处于太赫兹波段。对行星大气的辐射和吸收频谱进行测量,可获得行星大气的成分、比例、密度、温度和压力等参数信息,已成为深空探测领域的一种重要手段[1,2]。太赫兹波段谱线的测量需要用到超外差体制的高频谱分辨率谱仪(R=106~108)。整个太赫兹谱仪包括光路部分、接收机射频前端部分和接收机后端谱仪部分。在后端处理设备的谱仪选择中,有自相关频谱仪、声光频谱仪、滤波器组频谱仪、快速傅里叶变换频谱仪等。但是上述谱仪无法兼顾高频率分辨率和大带宽实时测量的要求,或者存在工作不稳定和难以校准的缺点[1,3]。因此,在深空探测领域Chirp 变换频谱仪得到了很好的应用,不仅可以克服上述频谱仪的缺点,还有着低功耗和抗辐射等优势。利用Chirp 变换频谱分析技术对行星大气进行大带宽精细谱探测,可以大动态范围、高稳定性探测谱线的多普勒频移情况,同时可实现超高频谱分辨率的谱线观测[3]。
Chirp 变换频谱分析仪有较多的应用。2004 年,欧洲空间局发射的罗塞塔(Rosetta)探测器搭载Chirp 变 换 频 谱 仪MIRO(Microwave Instrument ROSETTA Orbiter)对Comet67 P 彗星结构进行研究,分析了水、氨气和二氧化碳等气体分子辐射的红外谱线形状[4]。2010 年美国国家航空航天局(NASA)和德国宇航中心(DLR)合作的SOFIA(Stratospheric Observatory For Infrared Astronomy, SOFIA)项目,使用搭载着Chirp 变换频谱仪的波音747 飞机对高空的分子谱线测量,进一步对地球表面和大气构成、星际物质等进行了探索研究[5]。预计2022 年欧空局发射的木星冰卫星探测器(JUICE),其上搭载着Chirp 变换频谱仪的亚毫米波仪器(SWI),将调查木星平流层的温度分布、化学成分和动力学以及与其他大气区域的耦合[6]。
中国的Chirp 变换频谱仪研究始于20 世纪90年代,中国科学院声学研究所研制的带宽40 MHz、分辨率40 kHz 的Chirp 变换谱仪应用于紫金山天文台青海德令哈站13.7 m 射电望远镜,1999 年应用于乌鲁木齐25 m 射电望远镜水脉泽源的观测[7,8]。近些年,因Chirp 变换谱仪在毫米波望远镜和深空探测领域应用的突出优势,得到了广泛关注,2017 年中国科学院国家空间科学中心与声学研究所合作开展了400 MHz 带宽的Chirp 变换频谱仪研究,但是系统分辨率、主旁瓣电平比等关键参数与理论值相比仍有较大差距,不能满足深空探测应用的要求[9,10]。
本文针对深空探测的需要,设计研究了Chirp 变换频谱分析仪系统,并结合文献[11]对Chirp 变换频谱仪设计的一些问题进行分析。采用数字技术与模拟技术相结合的方式,可更为灵活地调整系统设计,提高系统匹配程度,改善系统性能,设计研究的Chirp 变换频谱分析仪系统分析带宽为400 MHz,频谱分辨率达到100 kHz,为中国深空探测领域的Chirp变换频谱分析仪系统研制奠定了基础。
1 Chirp 变换谱仪原理及灵敏度分析
Chirp 变换算法是实现Chirp 变换谱分析系统的基础,其是一种时频域变换运算,由傅里叶变换转化得到。
从傅里叶变换出发, 有

从式(5)可以看出,输入信号先与一个Chirp 信号相乘,再与一个Chirp 信号卷积,最后与一个Chirp 信号相乘,可以得到输入信号的傅里叶变换(M-C-M,这里M 代表相乘运算,C 代表卷积运算),用于产生第一个相乘Chirp 信号的器件称为展宽线,用于卷积的器件称为压缩线,第三个Chirp 信号在式(5)中只作用于输入信号的相位,还原信号的相位信息,因此在频谱分析中舍去,即Chirp 变换写为M-C。Chirp 变换过程如图1 所示。

图1 Chirp 变换谱分析原理Fig. 1 Chirp transform spectrum analysis principle diagram
M-C 运算有两种形式,当展宽线产生的Chirp 信号色散时间比压缩线产生的Chirp 信号短时,即M(s)-C(l)形式,输入的被测信号持续时间不能超过展宽线信号的色散时间,不能满足对输入连续波信号的分析;当展宽线产生的Chirp 信号色散时间比压缩线产生的Chirp 信号长时,即M(l)-C(s),可分析连续波信号,带宽为展宽线信号与压缩线信号带宽之差。由于展宽线色散时间长于压缩线,会使持续时间为展宽线与压缩线色散时间差的输入信号频谱丢失。当展宽线信号的色散时间为压缩线色散时间的两倍时,单个分支能够以50%的效率实现Chirp 变换。图1所示为单分支原理。采用双分支设计结构,通过射频开关使双分支交替运行,即可实现对输入信号100%的处理效率。
2 400 MHz 带宽频谱分析仪系统的设计与实现
研制的Chirp 变换谱分析仪系统采用数字技术与模拟技术相结合的方式,即数字波形合成方法产生Chirp 信号作为展宽线,声表面波线性调频信号发生器实现压缩线功能,二者进行匹配实现中心频率2 GHz、带宽400 MHz 输入信号频谱成分的分析。采用模拟与数字相结合方式实现的系统具有实时性好、功耗低、体积小、成本低等优点。
Chirp 变换谱分析仪系统主要由线性调频信号模块、射频调理电路模块和压缩线模块组成。线性调频信号模块产生Chirp 信号,经射频调理电路模块进行放大、倍频、滤波等过程达到系统展宽线的设计指标,被测信号与展宽线混频后,通过压缩线模块(声表面波线性调频信号发生器)生成脉冲信号。脉冲信号的时间节点与输入信号的频率信息相关,通过脉冲信号在时间轴分布的测量完成被测信号的频谱分析。图2 所示为系统的双分支电路结构,以单分支50%的效率实现Chirp 变换,得到输入信号100%效率的分析。
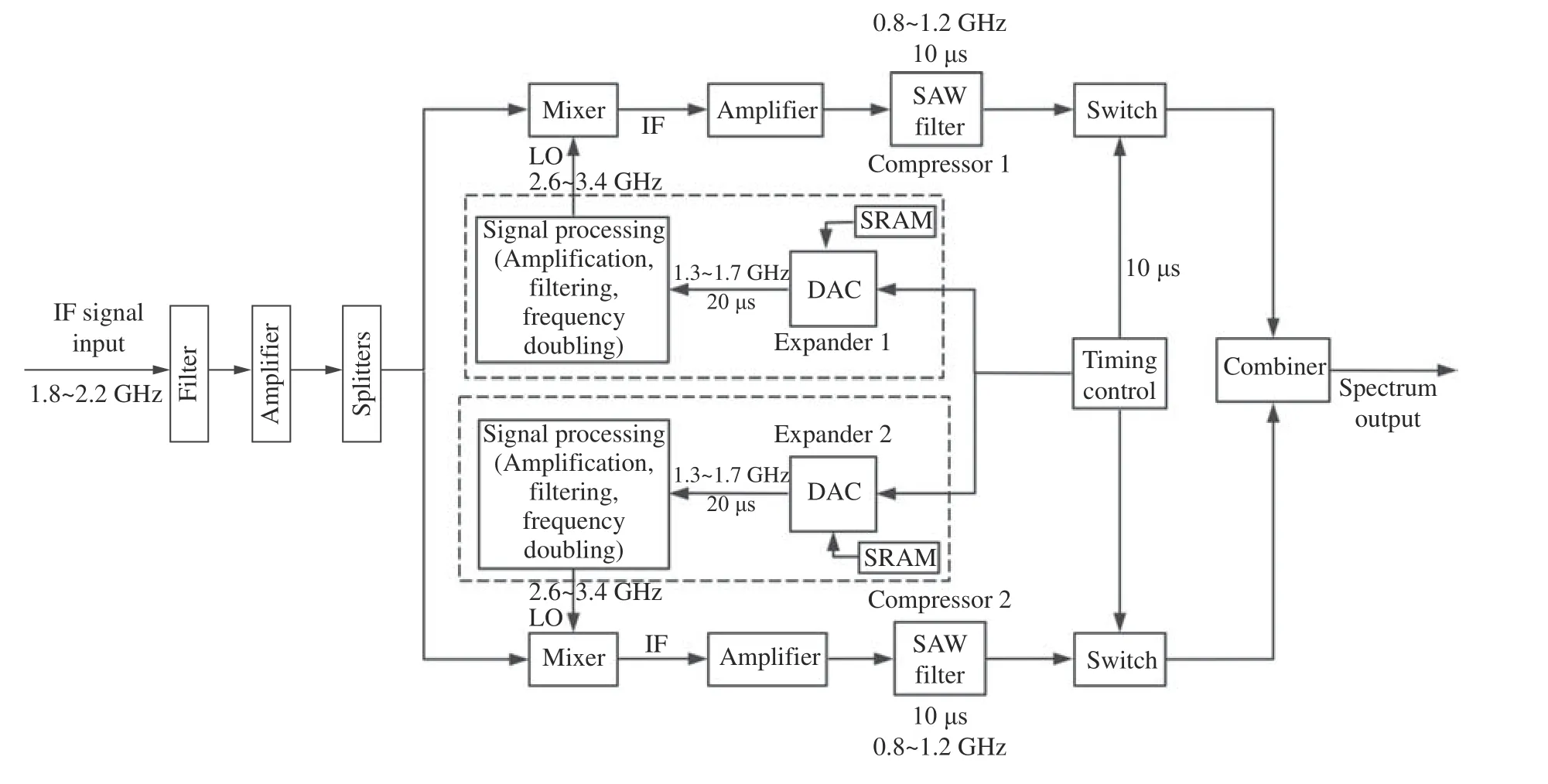
图2 Chirp 变换谱分析仪系统双分支电路结构Fig. 2 Chirp transform spectrum analyzer system double branch circuit structure diagram
线性调频模块产生频率为1.3~1.7 GHz、色散时间为20 μs 的Chirp 信号,信号调理模块的作用有三个:实现展宽线800 MHz 带宽要求;达到混频器对本振端的功率输入要求;抑制高频谐波并提高展宽线线性调频信号的信噪比。通过射频调理电路的构建,展宽线Chirp 信号达到系统设计要求。
压缩线采用的声表面波线性调频信号发生器为反射栅(RAC)阵列色散延迟线结构。反射栅阵列色散延迟线有更高的工作频率和更大的时宽带宽积。当发射换能器发出声信号时,信号中不同频率的成分在不同沟槽反射,其中高频信号和低频信号经过两次反射到达接收换能器的路径不同,高频信号经过路径较短,低频信号经过路径较长,从而实现了色散延迟。RAC 阵列色散延迟线中,声信号在沟槽中进行两次简单的机械反射,消除了各种二阶效应的影响。SAW 线性调频信号发生器的相频特性、带内相位均方根误差、频率–时间特性以及幅频特性如图3 所示,其中心频率为1 GHz,带宽400 MHz,色散时间10 μs,调频斜率–39.966 MHz·μs–1,相位均方根误差7.5°,插入损耗40 dB,带内平坦度小于2 dB。

图3 SAW 线性调频信号发生器性能参数。Fig. 3 SAW chirp signal generator performance parameters
3 基于SAW 压缩线的Chirp 信号展宽线匹配
3.1 带内单频输入信号的理论压缩结果
在Chirp 变换频谱分析仪的设计中,展宽线与压缩线的匹配度决定着系统性能。为验证展宽线与压缩线失配产生的影响,在MATLAB 中仿真了理想展宽线与压缩线的卷积结果。其中展宽线与压缩线调频斜率保持一致。
理想展宽线信号与压缩线信号压缩结果仿真如图4 所示,由于展宽线与压缩线卷积时,二者相位差不恒为某一固定值,导致压缩波形有较大差异。相位差不固定是由被测输入信号的相位和频率改变引起的。输入信号相位不固定,与展宽线相乘后,展宽线初始相位改变,压缩结果的波形出现差异。另外,展宽线带宽为800 MHz,压缩线为400 MHz,输入被测信号频率的不同,导致展宽线与压缩线卷积的频率段改变,使得相位差发生变化,压缩结果的波形也会出现较大差异。
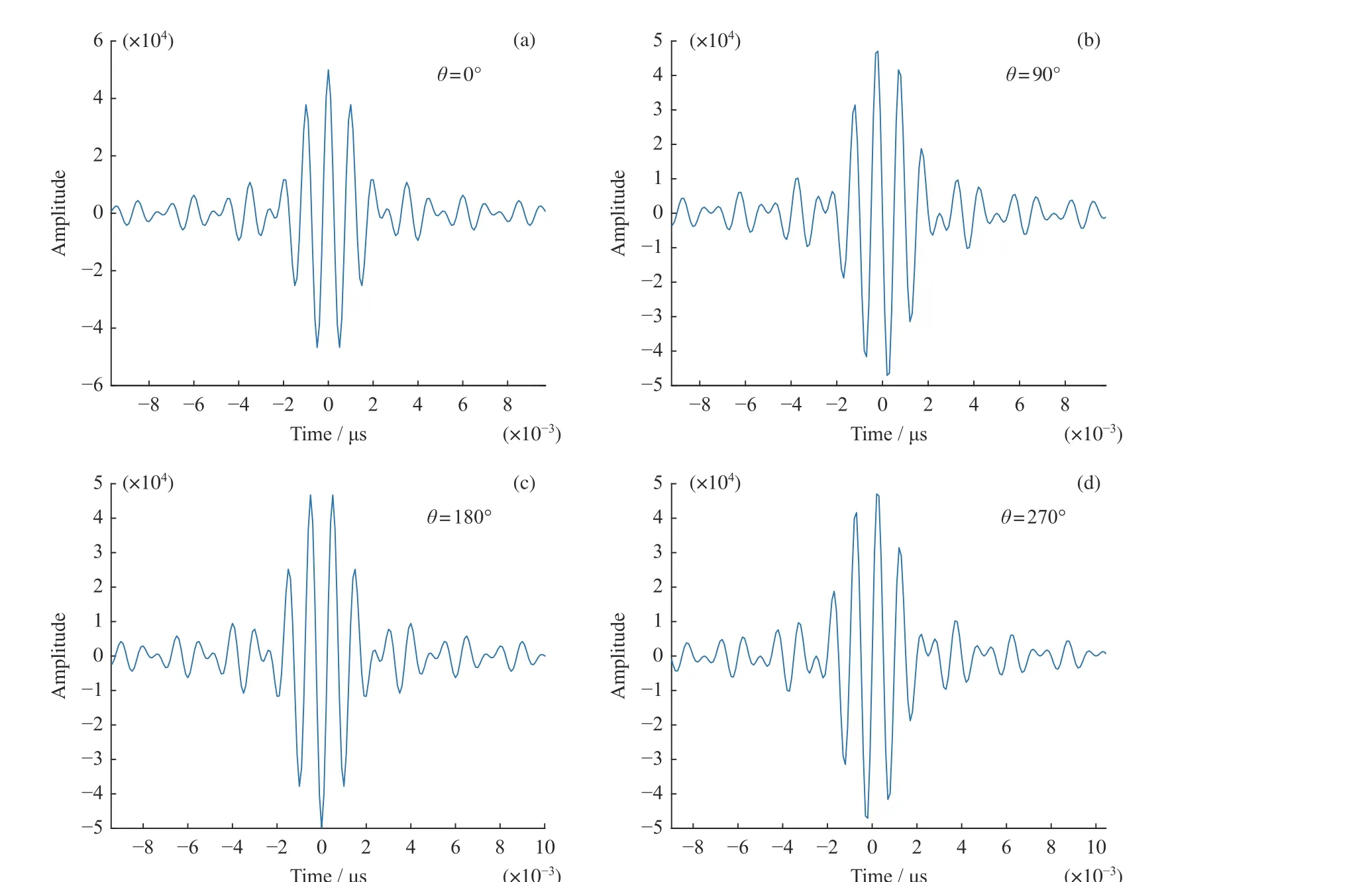
图4 展宽线与压缩线初始相位差θ 为典型值时系统压缩结果仿真Fig. 4 Initial phase difference between the expander and the compressor is θ, and the system compression result simulation diagram
为了消除展宽线与压缩线相位差的不确定导致压缩结果的差异,在一固定输入频率下,对随机初始相位的被测信号压缩结果进行叠加,观察压缩结果叠加后的波形,作为理想的展宽线与压缩线的压缩结果,仿真结果如图5 所示。
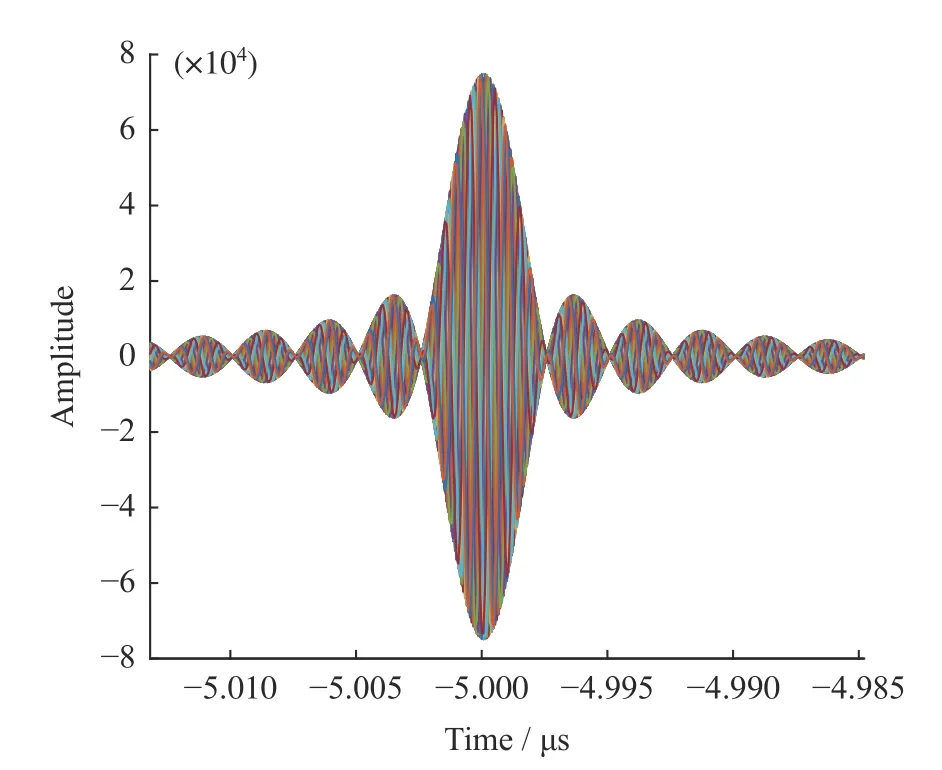
图5 在一固定输入频率下对随机初始相位的被测信号100 次理想仿真结果的叠加Fig. 5 Under a constant input frequency,the superposition of 100 ideal simulation results of the measured signal with random initial phase
虽然从波形也可以看出展宽线与压缩线的匹配程度,但为了更直观地展现压缩结果,增加了对压缩结果主瓣的脉冲宽度以及主瓣与最大旁瓣的峰值比(Peak Side Lobe Ratio, PSLR)的计算,以衡量压缩结果的优劣。由采样值确定峰值位置和幅度以及主瓣宽度的近似方法如图6 所示。从图6 可以看出,主瓣的–4 dB 带宽代表系统的分辨率,峰值旁瓣比体现在系统测量动态范围。理想压缩结果每一帧的输出时间宽度为10 μs,主瓣的–4 dB 脉冲宽度为2.5 ns(频率分辨率为100 kHz),峰值旁瓣比为13.26 dB[12]。
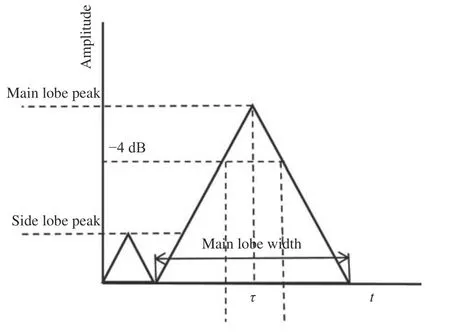
图6 主瓣的–4 dB 宽与峰值旁瓣比(PSLR)Fig. 6 –4 dB width of the main lobe and the peak side lobe ratio
3.2 数字展宽线与声表面波压缩线匹配压缩
设计构建的Chirp 变换频谱仪被测信号频率范围为1.8~2.2 GHz。当输入被测信号为2 GHz 时,系统的压缩结果如图7 所示。图7(a)为单次触发后示波器显示的一帧图。压缩结果被同步信号触发后,多帧叠加的结果如图7(b)所示。与理想的压缩结果对比,系统压缩脉冲左拖尾明显,旁瓣与主瓣混叠,难以区分,使得主瓣宽度远远大于理论值,系统的频率分辨率以及可测量的动态范围、灵敏度等参数不满足预期。通过分析系统的总体设计构建,应是展宽线与压缩线不完全匹配导致的压缩结果变差,主要体现在色散斜率的不匹配。分析其原因,主要为以下两方面。
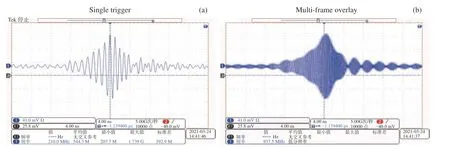
图7 2 GHz 被测信号输入的系统压缩结果Fig. 7 System compression result of 2 GHz measured signal input
(1)SAW 压缩线器件的问题。作为压缩线的SAW 器件,色散斜率K不是标准的40 MHz·μs–1,也不恒等于某一特定值,在带宽内并非处处相等。SAW线性调频信号发生器引起的相位偏差导致展宽线与压缩线的色散斜率相等时不为系统的最优压缩结果。
(2)射频调理电路的问题。在展宽线的生成中,因DAC 直接产生的Chirp 信号功率、带宽等不满足系统设计要求,需通过加入模拟器件改善Chirp 信号,但是也不可避免地使系统变得更为复杂,引入了更多变量。一方面模拟器件的相位失配,会使得展宽线色散斜率出现与压缩线同样的情况,带宽内不处处相同,展宽线与压缩线的匹配更加困难。另一方面,模拟器件在不同频率下的响应不一致,导致不同频率段展宽线的色散斜率偏差较大,会出现不同频率段压缩结果差异较大的现象。
针对上述情况,为了使数字展宽线和声表面波压缩线匹配,应先实现输入信号为单频点时的系统最优匹配,再从带宽内各个频点的最优匹配找到系统在整个带宽内的最佳匹配结果。
3.3 单频输入信号脉冲压缩的Chirp 信号调频斜率优化
应用数字方法的基带正交调制法产生的展宽线,可以提供期望色散斜率的Chirp 信号,这在需要纠正色散偏差时显得尤为重要。为了找出最佳的匹配色散斜率,通过写入不同色散斜率的Chirp 信号数据动态更新DAC 输出信号,比较主瓣宽度及峰值旁瓣比(PSLR)来判断压缩效果。
调节展宽线的色散斜率,可明显看到压缩波形的变化。绘制了被测信号输入为2 GHz 时,展宽线在不同色散斜率下压缩结果中两个关键参数的对比。从图8 和图9 可看出,展宽线色散斜率在39.95 MHz·μs–1附近时,左右旁瓣可明显区分,无拖尾现象,主瓣宽度较小,峰值旁瓣比高,压缩结果较好,系统匹配良好,单次触发结果与理论基本一致。当展宽线色散斜率超过39.965 MHz·μs–1或低于39.935 MHz·μs–1时,压缩结果变差,压缩波形拖尾严重,系统失配。以此确定2 GHz 信号输入的系统,展宽线最优色散斜率为39.95 MHz·μs–1。

图8 展宽线色散斜率不同取值下系统压缩结果中主瓣宽度与峰值旁瓣比(PSLR)的测量结果Fig. 8 Measurements of the main lobe width and Peak Side Lobe Ratio (PSLR) in the system compression results for different values of the dispersion slope of the expander
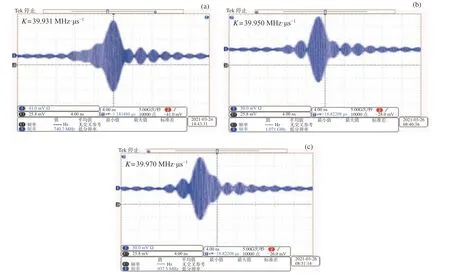
图9 展宽线色散斜率为一些典型值时系统在2 GHz 输入信号下的压缩结果Fig. 9 Compression result of the system at 2 GHz when the dispersion slope of the expander is of some typical value
3.4 带内Chirp 信号调频斜率优化
对于1.8~2.2 GHz 全频段测量,以50 MHz 为间隔,确定了输入信号在不同频率下的最优色散斜率,如图10 所示。
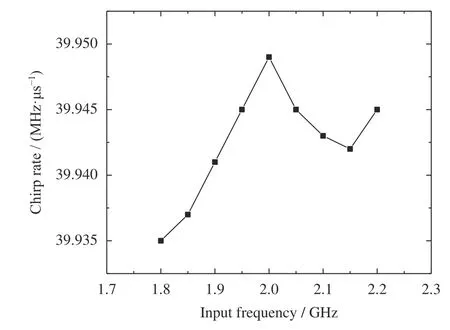
图10 在400 MHz 带宽内,以50 MHz 为测量间隔的测试系统最优色散斜率Fig. 10 Tested optimal dispersion slope of the system in the 400 MHz bandwidth with 50 MHz as the measurement interval
为了确定系统的展宽线最优匹配斜率,在不同输入频率下,取最优色散斜率附近值也可能会使压缩结果偏差较大。全频段出现最多的最优色散斜率为39.945 MHz·μs–1,也就是说展宽线K为此值时,在更多的频段下系统匹配最优,压缩结果较好,故本文采用39.945 MHz·μs–1作为全频段的最优色散斜率。比较展宽线色散斜率在39.945 MHz·μs–1时,不同输入频率下系统压缩结果的两个关键参数变化如图11所示。
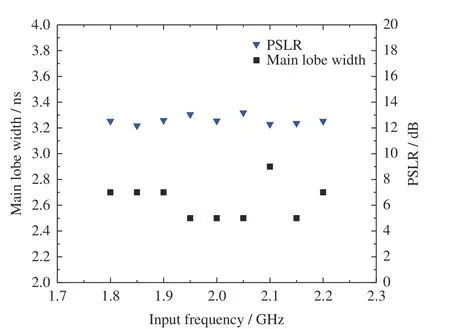
图11 在最优匹配色散斜率下(K=39.945 MHz·μs–1)系统在1.8~2.2 GHz 频带内的峰值旁瓣比(PSLR)和主瓣宽度的变化趋势Fig. 11 Peak Side Lobe Ratio (PSLR) and main lobe width of the system in the 1.8 GHz to 2.2 GHz frequency band under the best matched dispersion slope (K=39.945 MHz·μs–1)
系统频率分辨率在压缩结果中的表现为主瓣–4 dB 带宽,动态范围表现为压缩脉冲峰值旁瓣比。展宽线色散斜率为39.945 MHz·μs–1时,主瓣宽度小于2.9 ns,多个频率点位于2.5 ns,频率分辨率小于116 kHz,多个频段为100 kHz,接近理论值。全频段峰值旁瓣比均超过12 dB,接近理论值13.26 dB。因此,本设计采用39.945 MHz·μs–1作为最优的展宽线色散斜率与压缩线匹配构建系统。图12 为展宽线色散斜率为最优值时,Chirp 变换频谱仪在几个特定频率下的压缩结果。
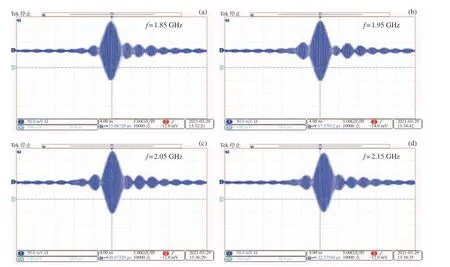
图12 展宽线色散斜率为39.945 MHz·μs–1 时系统在不同频点的压缩结果Fig. 12 Compression results of the system at different frequency points when the chirp rate of the expander is 39.945 MHz·μs–1
4 频谱分辨率分析
理想的压缩结果主瓣–4 dB 宽为2.5 ns,系统的理想频谱分辨率为100 kHz。不相干的两被测信号输入,其相位差( Δθ)的变化会使系统压缩结果发生改变。如图13 所示,虽然两信号频率都相差100 kHz,当两输入信号相位差0°,两压缩脉冲同相叠加,形成一个压缩脉冲,两信号难以区分;当两信号相位差90°,两压缩脉冲不相关,但振幅基本相同,形成一类似带宽信号的压缩脉冲;当两信号相位差180°,两压缩脉冲反相相消,两脉冲之间波形完全抵消,形成两个鲜明的脉冲。综上,当两信号相位差小于90°时,两信号压缩脉冲间的波形会叠加,使得振幅超过两压缩脉冲,分辨不出两信号真实频谱;当两信号相位差大于90°时,两信号压缩脉冲间的波形会抵消,使得振幅低于两压缩脉冲,可还原被测信号真实频谱。压缩脉冲的主瓣宽度为5 ns,即被测信号频率差大于200 kHz 时,两压缩脉冲可完全分开。


图14 所示为系统分辨率测试方法。两台信号发生器分别产生两个单频信号进入合路器,整合为一路信号进入频谱仪系统,信号的频谱信息将表现为在时间轴上不同时间节点的压缩脉冲,展现在示波器上。分别测试了2 GHz 输入信号和2.0002 GHz,2.00012 GHz, 2.0001 GHz 输入信号,频率间隔分别为200 kHz, 120 kHz, 100 kHz,并与理想仿真结果进行对比,如图15 所示。仿真图13 为MATLAB 产生的两随机初相输入信号与展宽线混频后,与压缩线卷积50 帧压缩结果的叠加。搭建的Chirp 变换谱分析仪200 kHz, 120 kHz, 100 kHz 分辨率测试结果与理论结果一致。其中,频率相差200 kHz 的压缩结果,两压缩脉冲主瓣可完全分开;120 kHz 时,两压缩脉冲幅值略高于中间的叠加波形;100 kHz 时,虽然中间叠加波形高于两压缩脉冲,但是此压缩结果为示波器的测量结果,为多帧随机相位输入信号压缩结果的叠加,不是固定90°相位差时的结果,因此中间波形略高于两压缩脉冲,计算多帧压缩结果的功率可直观地分辨频率差为100 kHz 的输入信号。必须指出的是,本文完成了示波器多帧叠加输出与理论分析的灵敏度比较研究,Chirp 变换谱仪的最终性能取决于数据采集等后续处理方法,以上分析表明本文研制的400 MHz带宽声表面波Chirp 变换谱分析仪达到了理论频率分辨率100 kHz。
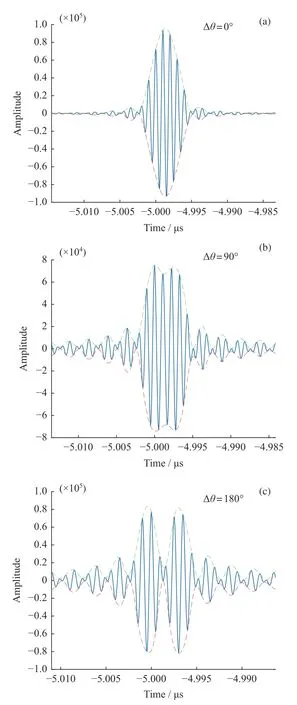
图13 两输入信号频率相差100 kHz 相位差( Δθ)不同时系统的压缩结果Fig. 13 When the frequency difference between the two input signals is 100 kHz and the phase difference is different
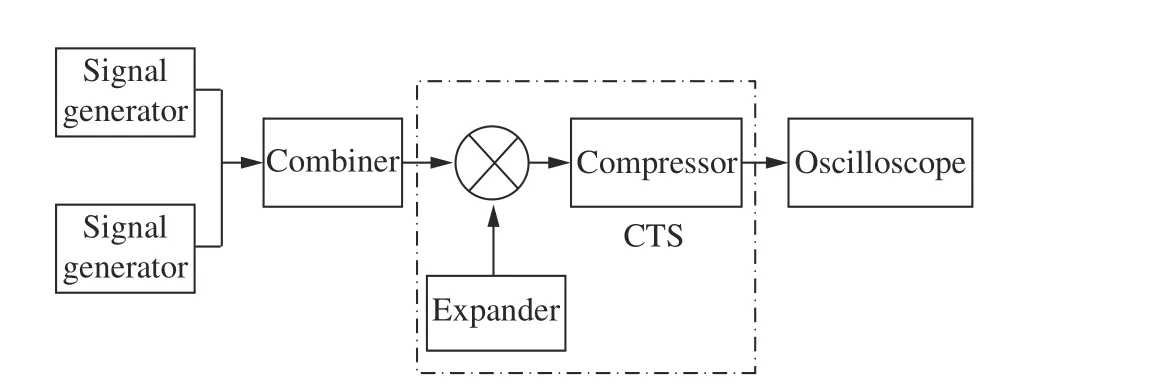
图14 CTS 系统分辨率测试Fig. 14 CTS system resolution test chart
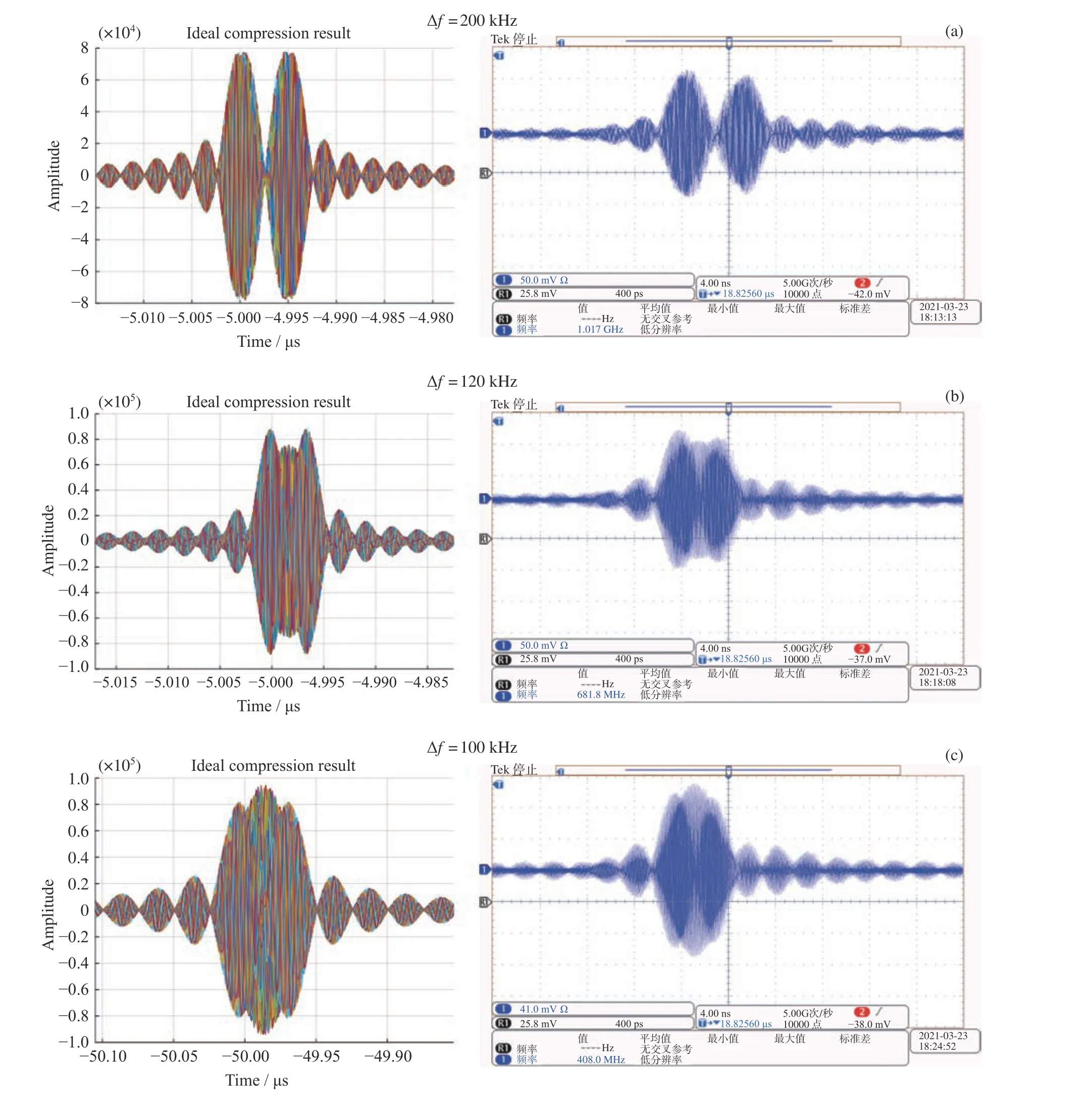
图15 系统分辨率测试结果Fig. 15 System resolution test result
5 典型输入的压缩结果
5.1 调频信号
调频信号具有丰富的频谱成分,对调频信号的检测,可直观表现系统的实时分析带宽。被测信号输入一调频信号,中心频率为2 GHz,最大频偏±640 kHz,通过Chirp 变换,谱分析仪系统在示波器上的显示结果如图16 所示,Chirp 变换频谱仪测量的频谱信息表现为在时间上的分布,频率偏移1.28 MHz,对应在时间轴上为32 ns,与理论分析结果一致。
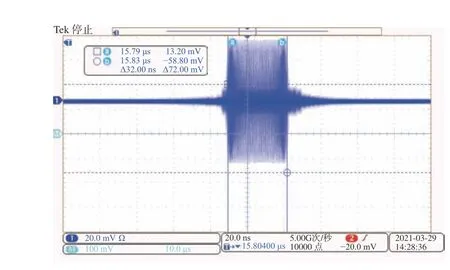
图16 调频信号经过Chirp 变换谱分析仪系统后的压缩结果Fig. 16 Compression result of FM signal after Chirp transform spectrum analyzer system
5.2 多频点信号的测量
为更直观地表现Chirp 变换频谱分析仪的频谱分析功能,测试了不同输入频率信号的压缩脉冲谱线,如图17 所示。从左往右,从上往下,依次为1.8 GHz 与1.9 GHz, 2.0 GHz, 2.1 GHz, 2.2 GHz 被测信号的压缩脉冲。被测信号经过Chirp 变换频谱仪系统,谱信息将转化为时间域的时间节点,并且400 MHz 带宽谱信息将与10 μs 时间节点一一对应。理论上,1.8 GHz 与1.9 GHz, 2.0 GHz, 2.1 GHz,2.2 GHz 被测信号的压缩脉冲时间间隔分别相差2.5 μs, 5 μs, 7.5 μs, 10 μs。图17 为示波器观察到的多频点输入信号测量结果。使用MATLAB 分析示波器采集到的压缩结果,计算各频点的时间间隔,确定系统在不同频点的频率偏差值。以1.8 GHz 被测信号的压缩脉冲作为时间基准,分别计算各频点与1.8 GHz 被测信号压缩脉冲的时间间隔及频率偏差(见表1)。

图17 多频率点信号经过CTS 系统后的压缩结果Fig. 17 Compression result diagram of multi-frequency signal after CTS system
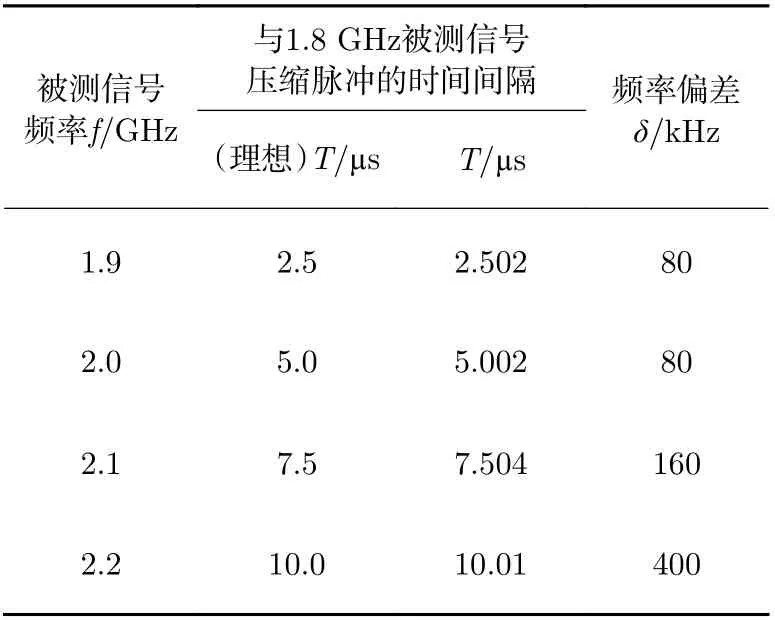
表1 不同频段的频率偏差Table 1 Frequency deviation of different frequency bands
由于采集装置的最小采样间隔为2 ns,因此1.9 GHz 与2.0 GHz 被测信号的频率偏差在误差范围之内,频率偏差小于80 kHz。2.1 GHz 与2.2 GHz被测信号压缩脉冲距离1.8 GHz 基准信号的压缩脉冲较远,频率相差较大,会产生较大的线性频偏叠加值,表现出较大的频率偏差。频率偏移量会在后续工作的信号处理算法中得到修正。
6 结论
Chirp 变换频谱仪具有功耗低、稳定性高等优点,在深空探测领域具有独特的应用优势。针对深空探测的需要,采用数字展宽线技术与声表面波压缩线技术相结合的方式,设计并构建了大带宽、高灵敏度的Chirp 变换频谱分析仪系统。设计的Chirp 变换频谱分析仪系统,压缩结果在多个频段主瓣–4 dB 宽为2.5 ns,可分析频率间隔最小为100 kHz 的信号,峰值旁瓣比超过12 dB,达到了系统的理想分辨率。系统实时处理带宽为400 MHz,可捕获大带宽内快速变化的谱信息。通过对调频信号与多频率点信号的测量,Chirp 变换频谱仪表现出的高分辨率及大带宽,使得其在深空探测中能够对超精细谱线和多普勒频移谱线成功探测,为中国在深空探测领域应用Chirp 变换频谱仪奠定基础。
