多根无限长恒定电流形成的磁力线方程研究

郭 勇 姜付锦

(1.湖北省孝感高级中学 432100；2.湖北省黄陂一中试题研究中心 430300)

1 问题

四根均通有恒定电流的长直导线1、2、3、4都垂直于x-y平面，它们与x-y平面的交点是边长为2a、中心在原点O的正方形的顶点，各导线中电流的方向已在图1中标出.

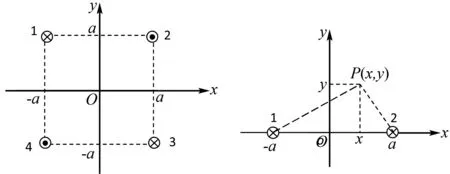
图1 图2

已知真空磁导率为μ0.试分析空间磁力线方程是怎样的？是如何分布的？

2 磁力线方程推导

2.1 两根无限长电流形成的磁力线方程

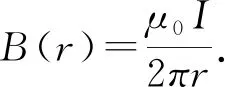
将上式两边不定积分后得

I2·ln[y2+(x-a)2]+I1·ln[y2+(x+a)2]=C，(C为一个积分常数)

进一步整理后得

[y2+(x+a)2]I1·[y2+(x-a)2]I2=eC，

若I1=I2，则磁力线方程是到两个定点(直线电流)的距离之积是一个定值.

若I1=-I2，则磁力线方程是到两个定点(直线电流)的距离之商是一个定值.

2.2 四根直线电流形成的磁力线方程

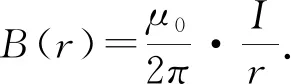
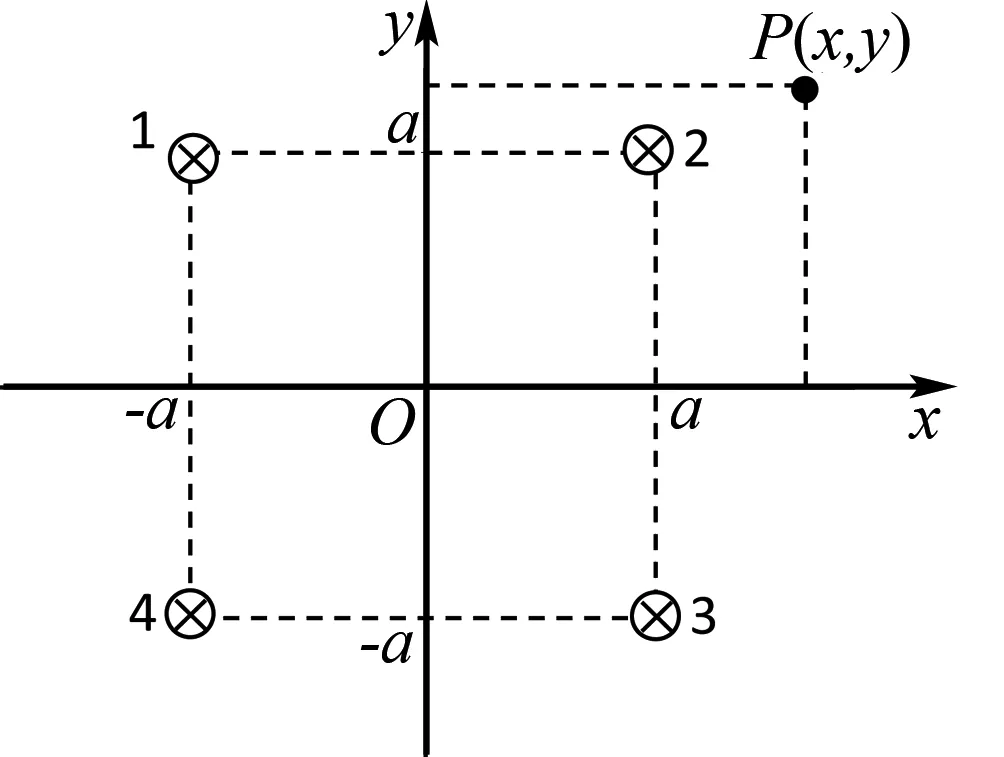
图3

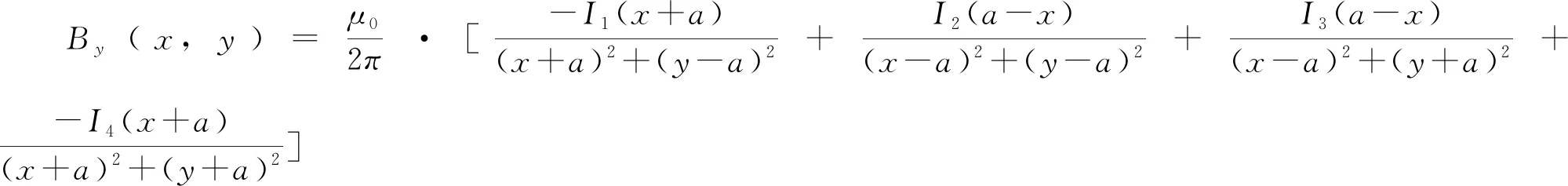
整理后得

两边不定积分后得

[(y-a)2+(x+a)2]I1·[(y+a)2+(x+a)2]I4·[(y-a)2+(x-a)2]I2·[(y+a)2+(x-a)2]I3=C1，

若I1=I3=-I2=-I4，则

上式中C1为某一个积分常数，这个曲线簇就是本文开始问题的答案.

2.3 n根直线电流形成的磁力线方程

不妨设互相平行的n根无限长直线电流，通过它们的电流依次为I1,I2,I3,…,In，位置坐标依次为(x01,y01),(x02,y02),(x03,y03),…,(x0n,y0n)，则它们在空间形成的磁力线方程如下：

[(y-y01)2+(x-x01)2]I1·[(y-y02)2+(x-x02)2]I2…[(y-y0n)2+(x-x0n)2]In=C，

上式中C为某一个积分常数.

2.4 由柯西——黎曼方程推导

设磁势为φ，磁感应强度为B，由于B=-∇φ，得任意一点P(x,y)的磁感应强度为

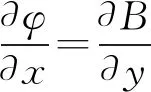
积分后得B(x,y)=I2·ln[y2+(x-a)2]+I1·ln[y2+(x+a)2]+k(x)

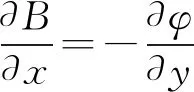
k(x)=C1(C1为任意常数)，得

B(x,y)=I2·ln[y2+(x-a)2]+I1·ln[y2+(x+a)2]+C1

上式中的B(x,y)为任意常数，则上式可化为

I2·ln[y2+(x-a)2]+I1·ln[y2+(x+a)2]=C

上式中C1为任意常数，即两根无限长直线电流形成的磁力线方程.

2.5 数值模拟

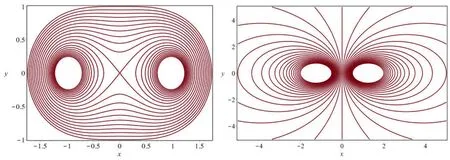
图4 图5

通过以上分析可以现，多根无限长通电直线形成的磁力线方程既可以用磁力线的微分方程推导，也可以由柯西——黎曼方程得到.它们形成的磁力线方程与多根无限长均匀带电直线的等势线方程具有类似性，若它们的电流大小相等、方向相同，则磁力线方程是到这些电流位置的距离的乘积是一个定值的曲线簇——卡西尼卵形曲线.限于篇幅，这里不再赘述，感兴趣的读者可以自行推证.