空间旋转目标消旋力矩仿真分析*

石永康 黄少华 廖 潜 陈金山

(新疆大学机械工程学院 乌鲁木齐 830017)

0 引言

分布于地球外层卫星轨道的空间碎片占用轨道资源并对现役航天器造成极大威胁。2021 年3 月10 日美国已退役气象卫星NOAA17 发生解体，分裂成16 块碎片，同年3 月18 日，中国气象卫星云海一号02 也在其轨道上发生解体，分裂成21 块碎片。为有效利用空间资源，减少空间碎片密度及碰撞趋势，空间碎片主动清除技术（Active Debris Removal,ADR）相关研究引起了广泛关注[1]。

电磁消旋是基于法拉第电磁感应定律和楞次定律的一种消旋制动方式。大部分空间碎片表面材料为非磁化金属导体，在外加磁场的作用下，由于自身旋转产生表面涡电流，涡电流在原磁场的作用下产生与旋转方向相反的制动力矩，使得旋转速度逐渐降低，便于接触式主动清除技术装备对碎片进行抓捕[2]。国内外学者对电磁消旋进行了大量理论推导和相关实验研究。Gómez 等[3,4]对涡流进行分析，构建了基于电磁张量的球壳模型消旋力矩表达式，针对非均匀磁场，加入有效因子对表达式进行修正，研究了不同线圈半径和线圈—目标重心距离下的消旋力及消旋力矩。Shi 等[5]基于第二代高温超导技术，提出了超导式涡流消旋的概念，通过电磁张量建立了精确的磁场模型和涡流力矩模型，并对超导式涡流消旋的制动性进行定量分析，论证了超导式涡流消旋的技术水平和制动能力。Chu[6]基于球壳模型的消旋力矩公式，仿真分析了球壳模型转速、表面材料电导率、外加磁场及球壳尺寸对消旋力矩的影响，得到各因素影响下消旋力矩的变化趋势，但未通过有限元仿真进行验证计算，且未考虑各因素取值下的消旋力矩公式的适用性。Sun[7]通过解析法得到线圈的最佳半径、最佳安匝数及目标之间的最佳作用距离，并通过有限元法进行了仿真验证，但是未分析目标本身尺寸、厚度等对消旋力矩的影响，且未将各因素与理论公式联系进行分析。

综上所述，目前对于电磁消旋技术的研究主要集中在消旋方案、地面消旋实验装置设计以及理论分析与数值分析方面。消旋目标的尺寸和厚度对消旋力矩影响的相关研究较少。球壳模型消旋力矩解析式的适用性，以及单因素对球壳模型消旋力矩的影响与多因素对球壳模型消旋力矩的影响之间的关系，尚未见到相关研究。消旋力矩的影响因素分析是探究电磁消旋过程、提高消旋效果的关键，由于电磁场有限元方法具有计算精度高且能够分析各种复杂形状模型等优势，使用有限元方法对电磁消旋技术进行仿真分析具有重要意义。

1 电磁消旋原理及仿真模型验证

1.1 电磁消旋原理

电磁消旋由线圈产生的磁场与旋转导体表面涡电流之间的相互作用力产生。电磁消旋广泛应用于高速列车的电磁制动过程中[8,9]。图1 所示为旋转导体在磁场中感生出的涡电流及在磁场相互作用下产生的作用力。

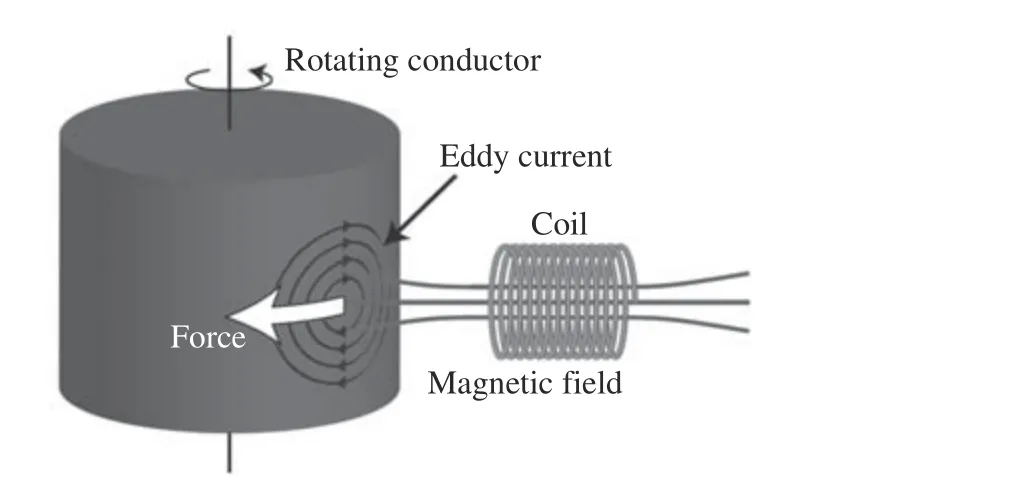
图1 电磁—涡流消旋概念Fig. 1 Damping by electromagnetic eddy currents

当旋转轴方向与磁场方向不平行，旋转导体置于磁场中时会切割磁感应线产生涡流。旋转导体在原磁场和感生出的涡电流的相互作用下逐渐消旋[10]。

1.2 匀强磁场区域磁感应强度

亥姆霍兹线圈可以营造出匀强磁场，如图2 所示[11]。一对半径为R的线圈相对放置，间距为a，两线圈中心分别为O1和O2。因为线圈中所通电流方向一致，所以两线圈产生的磁场方向一致，可以代数叠加，表现为图2 中曲线所示的状态。

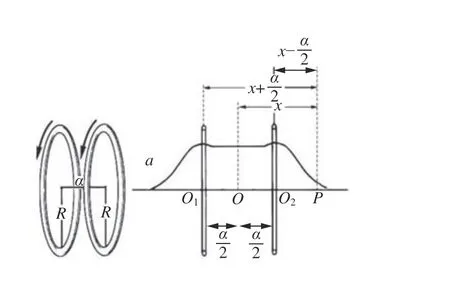
图2 亥姆霍兹线圈Fig. 2 Helmholtz coil

取线圈对的中心连线中点作为坐标原点O，在轴上距O点x处 取任意点P，则P点到两线圈中心的距离分别为x+a/2和x-a/2。 两线圈在P点产生的磁场大小分别为

1.3 球壳消旋力矩解析式

电磁消旋目标为失效卫星、航天器爆炸产生的碎片、火箭上面级等，其形状和尺寸大小不一，无法建立统一的几何模型进行描述。此外，由于电磁消旋机理复杂，对于复杂几何体的计算较为困难，因此选取结构较为简单的球壳模型作为研究对象。实际情况下也存在类似结构，例如东方红一号卫星，在实际计算过程中可忽略其他结构对消旋力矩产生的影响，只考虑卫星蒙皮的消旋效应。

匀强磁场中，球壳所受到的消旋力矩的解析式如下[3]：

其中，R′为 球壳外半径（球壳半径），e为 球壳厚度，σ为球壳材料的电导率，ω为球壳的旋转角速度，B为球壳模型重心(Centre of Gravity, COG)位置的磁感应强度。

当球壳的旋转轴为z轴，匀强磁场的方向指向y轴正向时，球壳的消旋力矩解析式可写为

标量形式为

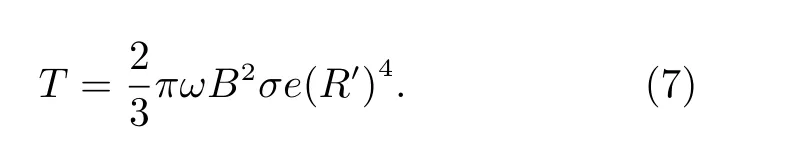
1.4 二维亥姆霍兹线圈仿真模型及其有效性验证

因MAXWELL 涡流场无法仿真固定磁场对旋转目标体的涡流阻力矩，参考文献[12]在研究高速列车电磁制动时使用的动态磁场相对固定目标的求解涡流分布的方法，在MAXWELL 涡流场中建立旋转磁场，利用旋转磁场对固定目标的消旋力矩代替固定磁场对旋转目标产生的涡流阻力矩。

为建立旋转磁场，设置两组线圈对，相对的两线圈通有大小相等、方向相同、初始相位角也相同的正弦交流电，相邻的两线圈对则通有大小相等、方向相反、初始相位角相差90°的正弦交流电[6]。在仿真过程中，相同尺寸线圈会产生几何干涉而对计算结果产生影响，因此将一组线圈对的半径和间距设置为2 m，给定初始的电流大小为123.8 A，将另一组线圈对的半径和间距设置为2.1 m。为使两组线圈对在O点处产生的磁感应强度相等，根据式(4)可计算出半径为2.1 m的线圈中所通电流为130 A。在MAXWELL中建立的二维亥姆霍兹线圈仿真模型（线圈模型）和球壳仿真模型（球壳模型）如图3 所示。

图3 线圈模型和球壳模型Fig. 3 Finite element model of coil and spherical shell

球壳模型的内半径r=0.5 m，外半径R′=0.51 m，则球壳的厚度e=0.01 m，材料为型号2A01 的铝合金，电导率σ=2.32×107S·m—1，旋转速度ω=(π/2)rad·s—1。

求解完成后，在球壳模型的Oxy截面上等角度选取10 个点，每点与圆心之间的距离为0.01 m，得到各点的磁感应强度如表1 所示。

表1 中心区域磁感应强度大小Table 1 Magnitude of magnetic flux density of the center area

磁感应强度的平均值B=5.40×10—5T。将B=5.40×10—5T 代入式(7)，式(7)中的磁感应强度为球壳稳定旋转时重心(COG)处的磁感应强度，因此可直接使用仿真得到的磁感应强度平均值进行计算。得到消旋力矩的解析解T=1.506×10—4N·m，MAXWELL 仿真得到旋转磁场对球壳消旋力矩的数值解T=1.442×10—4N·m，绝对误差为4×10—7N·m，相对误差为4.27%，小于5%，在误差允许范围内。因此在MAXWELL 中建立的二维亥姆霍兹线圈仿真模型有效，可用于下一步的仿真实验研究。

2 球壳模型消旋力矩分析

参考匀强磁场中球壳的消旋力矩解析式(7)可知，消旋力矩与球壳表面材料电导率、匀强磁场磁感应强度、球壳的旋转角速度、球壳半径及球壳厚度相关。其中，匀强磁场磁感应强度可通过改变线圈电流大小实现，如1.4 节所述，由于MAXWELL 电磁仿真软件的限制，无法在涡流场中直接对球壳模型的旋转角速度进行设置，因此通过设置线圈电流频率的方法，间接设置球壳模型的旋转角速度。

2.1 单因素对消旋力矩的影响

航天器在发射、返回以及空间中运行时，会受到多种因素的影响，造成表面材料变性、设备失效等问题，从而影响航天器的正常运行。因此材料的选择对于航天器至关重要。常用的航天器材料为金属铝、钛、镁及其合金[13]。在不考虑温度对金属材料电导率影响的前提下，为研究材料对消旋力矩的影响，选取航天器常用的三种金属材料及其系列合金[14]进行消旋力矩的影响实验。由于不同金属材料的导电性不同，可选用电导率作为影响因素进行球壳表面材料对消旋力矩影响的仿真实验。MAXWELL 中具有丰富的材料库，可直接选用MAXWELL 中各金属材料默认的电导率参数值。这里共选取32 组材料进行仿真实验。

Tiesenhausen[15]提出使用通电线圈产生的磁场对旋转目标进行消旋，并研究了涡流效应对航天器姿态的影响。为研究外加磁场对消旋力矩的影响，通过改变线圈电流大小进行外加磁场对球壳模型消旋力矩影响的仿真实验。设定线圈电流的变化范围为13～273 A，间隔为13 A。

近地轨道和地球同步轨道的空间碎片旋转速度分别可达70(°)·s—1和400(°)·s—1[16]，在这种高速旋转的情况下，对旋转目标直接进行抓取或采用接触式消旋方案都具有极大的风险，因此在实施抓捕前需对旋转目标进行非接触式消旋。为研究同一线圈电流强度对高低速旋转目标的消旋效果，设定球壳模型的速度范围为(π/2～20π) rad·s—1，间隔为(π/2) rad·s—1，对应的电磁场频率变化范围为0.25～10 Hz，间隔为0.25 Hz。

对1.4 节仿真模型的匀强磁场区域进行分析，取图3 中Oxz截面上的磁场分布，如图4 所示。

图4 匀强磁场云图Fig. 4 Cloud map of uniform magnetic field

取图3 坐标系沿x轴方向上的磁感应强度分布，如图5 所示。其中，距坐标系原点0.65 m 处的磁感应强度B=5.3928×10—5T，坐标系原点处的磁感应强度B=5.4160×10—5T，差值为0.0232×10—5T，磁场均匀度小于0.5%，因此选取中心区域匀强磁场的范围为±0.65 m。为研究球壳半径对消旋力矩的影响，设定球壳模型的半径变化范围为0.25～0.65 m，间隔为0.05 m。

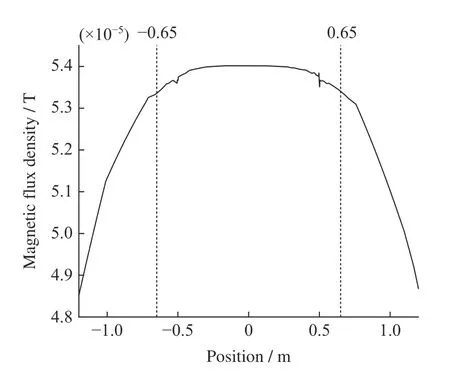
图5 中心区域匀强磁场分布Fig. 5 Distribution of uniform magnetic field in the center area

为研究球壳厚度对消旋力矩的影响，仿真过程中，设定球壳模型的厚度变化范围为1～40 mm，间隔为1 mm。

将以上条件赋予线圈模型和球壳模型，保持其他因素不变，分别得到各因素影响下，球壳模型的消旋力矩变化情况。为对比各因素对球壳模型消旋力矩的影响，将各影响因素横坐标值做归一化处理，如图6所示。

由图6 可知，随着球壳模型电导率的增加，消旋力矩呈现近似线性的增长关系。其原因是，电导率与球壳表面的电子迁移率成正比，并且球壳表面材料的电导率与电场强度之积为传导电流密度，因此球壳表面涡电流与球壳表面材料电导率成正比。随着线圈电流的增大，即随着外加磁场的增大，球壳模型的消旋力矩增加，且增幅明显。其原因是，随着线圈电流的增大，线圈产生的磁场强度增大，由式(7)可知，球壳的消旋力矩与磁感应强度的平方成正比，因此与其他因素相比，球壳的消旋力矩受线圈电流的影响较大。

图6 各因素影响下的球壳模型消旋力矩变化情况Fig. 6 Variation trend of damping torque of spherical shell model under various factors

在确定的磁感应强度下，球壳模型受到的消旋力矩随着半径的增大而增大，且增幅明显。其原因是，随着球壳半径的增大，垂直于磁场方向的球壳各截面的面积将增大，且截面面积与其半径的平方成正比。球壳旋转过程中，各截面切割磁感应线引起的磁通量变化增大，因此球壳表面感生出的涡电流增大，在相同磁场强度下，球壳受到的安培力增加，消旋力矩也增加。

随着球壳模型厚度的增加，消旋力矩呈近似线性增长。其原因是，球壳厚度的增加使得球壳单位截面上电荷通量增加，且电荷通量Q与球壳厚度h之间满足

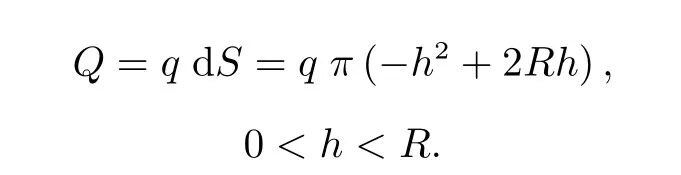
因此整个球壳受到的安培力增加，消旋力矩也增加，但增幅逐渐放缓。由于球壳模型的厚度只选取了[0,R]上极小的一段，因此仿真曲线呈现近似线性增长。在本文仿真案例中，当球壳模型的转速小于20 rad·s—1时，消旋力矩随着转速的增加而增大，当转速大于20 rad·s—1时，消旋力矩随着转速的增加而逐渐减小。其原因可能是，在低速旋转阶段，随着球壳转速的提高，球壳各截面的磁通量变化率变大，因此消旋力矩随着转速的增加而增大，当转速增大到临界值时，球壳表面的涡流感应电场明显增强，降低了球壳所处位置磁场的大小，此时球壳的消旋力矩随着转速的增加而减小。

根据球壳重心(COG)处的磁感应强度取值，结合式(7)，分别计算得到各因素影响下，球壳模型消旋力矩的理论值，并与仿真结果进行比较。将各影响因素的横坐标值做归一化处理，得到各因素影响下，球壳模型消旋力矩仿真值与理论值之间的相对误差，如图7 所示。

由图7 可知，在设定的仿真参数范围内，相对误差受球壳半径和厚度的影响最大；在球壳电导率、线圈电流（即外加磁场）、球壳旋转角速度的变化影响下，相对误差在4%附近。

图7 各因素影响下的相对误差Fig. 7 Relative error under the influence of each factors

球壳表面材料电导率、线圈电流、球壳旋转角速度影响下的相对误差如图8 所示。

由图8 可知，球壳表面材料电导率、线圈电流影响下的相对误差分布在4.2%～4.3%范围内，误差变化小于0.1%；在球壳旋转角速度影响下，相对误差逐渐降低，误差分布范围为3.7%～4.3%。引起误差的原因可能是仿真计算产生的累积误差，由于其误差变化几乎可以忽略不计，且误差分布范围相对均匀，因此认为球壳消旋力矩解析式可以较好地适应这三种因素的变化。

图8 电导率、线圈电流、球壳旋转速度影响下的相对误差Fig. 8 Relative error under conductivity, coil current and the rotation speed of the spherical shell

为进一步分析在球壳的半径和厚度影响下，球壳消旋力矩解析式的适用范围，将球壳的内半径a设定为0.50 m，厚度范围设置为1 ～40 mm，间距为1 mm，以球壳厚度h与 半径R′之比为横坐标，球壳消旋力矩的仿真值与理论值之间的相对误差（取绝对值）为纵坐标，结果如图9 所示。

图9 球壳的厚度与半径之比影响下的相对误差Fig. 9 Relative error under the ratio of the shell thickness to the shell radius

由图9 可知，随着球壳厚度与球壳半径的比值h/R′的增大，相对误差呈近似线性变化，当h/R′小于0.023 时，相对误差在5%以内。同时由图9 可知，仿真验证所用球壳厚度与半径的比值h/R′为0.0196，接近0.023。由此可知，上述各组仿真实验中，球壳消旋力矩的仿真值与理论值之间的误差，除仿真计算引起的累积误差之外，主要受球壳厚度和半径的影响。

由图8 和图9 可知，球壳半径或厚度单方面的增大都不是引起相对误差增大的直接原因。在满足匀强磁场的前提下，保证h/R′小于0.023，相对误差可控制在5%以内；当h/R′大于0.023 时，现有的球壳消旋力矩解析式不再适用。

2.2 精确球壳消旋力矩解析式

当球壳厚度h与球壳内半径r之比h/r ≪1时，球壳外半径R′和 球壳内半径r满足[17]

则式(7)可写为

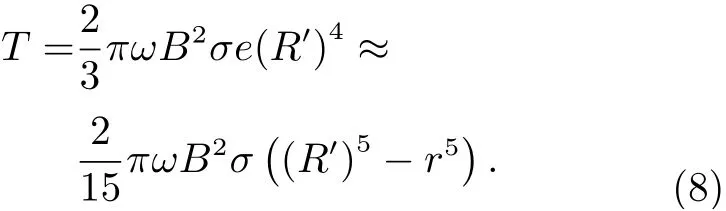
将式(8) 作为新的球壳消旋力矩解析式，对图7各因素影响下的相对误差进行重新计算，计算结果如图10 所示。同时，对图9 球壳的厚度与半径之比影响下的相对误差进行重新计算，计算结果如图11 所示。

图10 各因素影响下的相对误差Fig. 10 Relative error under the influence of each factor

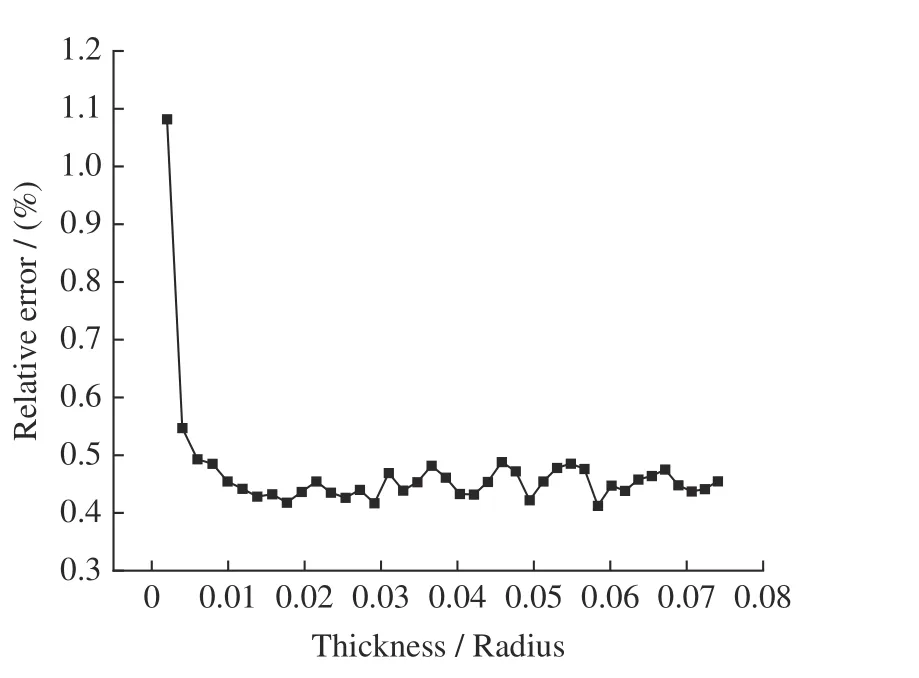
图11 球壳的厚度与半径之比影响下的相对误差Fig. 11 Relative error under the ratio of the shell thickness to the shell radius

由图10 和图11 可知，通过修正后的球壳消旋力矩解析式，计算得到的相对误差基本在1%以下，与现有的球壳消旋力矩解析式相比，计算误差更小。由图11 可知，针对h/R′＞0.023 的球壳模型，修正后的球壳消旋力矩解析式仍有较小的计算误差，相对误差基本稳定在0.4%～0.5%的区间范围内。误差来源主要分为两部分：一部分是二维亥姆霍兹线圈仿真模型误差，另一部分为仿真计算累计误差。

3 结论

针对提高空间旋转目标消旋效率的问题，分别对各因素影响下球壳的消旋力矩变化情况进行了研究。根据亥姆霍兹线圈设计原理，在MAXWELL 中设计并建立了二维亥姆霍兹线圈仿真模型，并对其进行有效性验证。从验证的仿真模型出发，分别分析了球壳表面材料电导率、线圈电流、球壳旋转角速度、球壳半径和球壳厚度对球壳模型消旋力矩的影响。并且对现有的球壳消旋力矩解析式进行了修正。主要结论如下。

（1）球壳的消旋力矩随着各因素数值的增加而增加。

（2）球壳消旋力矩解析式对球壳表面材料电导率、线圈电流、球壳旋转角速度的变化有很好的适应性。

（3）球壳的厚度与半径之比大于0.023 时，球壳消旋力矩解析式不再适用。

（4）修正后的球壳消旋力矩解析式与原有解析式相比，计算误差更小。