LEO 空间碎片甚短弧角度数据初轨确定方法对比*

雷祥旭 夏胜夫 杨 洋 王啸臻 张郑元 李振伟 桑吉章

1(山东理工大学建筑工程学院 淄博 255000)

2(中国科学院国家天文台 北京 100101)

3(武汉大学测绘学院 武汉 430079)

4(中国人民解放军63768 部队 西安 710600)

5(中国科学院国家天文台 长春人造卫星观测站 长春 130117)

0 引 言

随着航天技术的不断发展，人类空间探索活动越来越频繁，越来越多的航天器被送入太空，轨道碎片的数量随之大幅增长，空间目标之间的碰撞风险亦随之增大，航天器的安全运行面临着严重威胁。因此，近年来空间碰撞预警、航天器规避操作、空间碎片清除等技术的研究不断深入[1-5]。开展这些研究的前提是对空间目标进行有效的监测和编目。空间目标包括在轨工作航天器和空间碎片，空间碎片是人类遗留在空间的废弃物，包括完成任务的火箭箭体和卫星本体、火箭的喷射物、执行航天任务过程中的抛射物以及空间目标碰撞产生的碎片等[6,7]。

轨道确定是空间目标监测数据处理的主要步骤，按照处理过程可以分为初轨确定和轨道改进[8,9]，其中轨道改进又称为精密定轨。前者是在没有任何初始信息的前提下，利用短弧段的观测数据，采用比较简单的动力学模型（通常是二体模型）快速计算空间目标的初始轨道[10,11]。初轨确定的结果可以作为轨道改进的初始值，高精度的初轨参数可以节省精密定轨的时间，提高精密定轨的精度[12]。

初轨确定的方法有多种，包括Gauss 方法、Laplace 方法、Gooding 方法等经典算法[13,14]以及遗传算法[15]等现代算法。现有方法一般适用于几分钟到几十分钟的观测弧段，例如文献[12]发现弧长超过400 s 的弧段初轨确定结果较好，随着弧长增长，观测数据增多，定轨误差降低，但当弧长达到一定长度后，误差有所增大并最终趋于稳定。但实测场景为非跟踪模式观测时，空间目标角度观测数据弧长往往小于60 s，甚至不足20 s，有必要利用实际观测数据测试各算法的性能和可靠性。另外，上述算法各有特点，不同观测数据条件下的结果也有较大差别，为了在不同场景下得到尽可能精确的解，有必要进行不同方法之间的比较，比较结果有利于在不同场景下筛选最合适的算法，进而得到尽可能最优的解。

利用天基仿真角度数据和地基实测角度数据对现有的甚短弧初轨确定算法进行了测试和对比分析，得出了各种方法的优劣特性，可为相关轨道确定问题提供参考。

1 初轨确定方法

初轨确定涉及的算法主要包括Laplace 方法、Gauss 方法、Gooding 方法和距离搜索法。Laplace方法只需要被观测目标的三次光学测量即可进行求解，通过构造方程，利用首尾两时刻的观测资料，计算中间时刻的位置和速度，然后通过经典二体问题求解初轨参数。基于此，Laplace 方法只需要初始的光学观测资料，不需要任何初始值信息。该方法基本原理如下[12，14]。

在某时刻，空间目标观测方程如下：

式中，r为空间目标位置矢量，R为观测平台位置矢量，L为观测方向单位矢量，ρ为观测距离。对式（1）进行二次求导可得

其中，ρ,ρ˙,ρ¨ 和r为未知量，其他量均可通过观测值推导得到。假设给定r的初始值为r0, 式(5)可通过行列式和克莱姆法则求解，进而通过迭代求解得到最终的初轨参数。

Gauss 方法假设三个位置矢量都位于同一平面上，并根据几何关系引入f和g级数，建立关于目标位置矢量的方程式并求解[12,14]。根据三个位置矢量都位于同一平面上的假设，引入未知系数c1,c2,c3，有

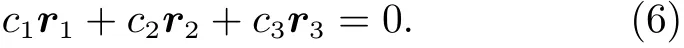
r1和r3分别叉乘式（6），可得

通过引入f和g级数的方式，可以把首尾两时刻的位置矢量r1和r3表 示为中间时刻位置矢量r2和速度矢量r˙2的函数，通过变换处理，最终可通过类似于Lambert 问题的方式求解空间目标的轨道根数解。

文献[14]和[16]提出了一种完全不同的方法，其基本原理是通过观测距离的迭代估计，将角度问题转换为Lambert 问题（已知两个时刻的位置矢量求解开普勒轨道参数），称为测距迭代方法。在测距迭代方法的基础上，Gooding 又提出一种新的方法[13]。同样是基于观测距离的迭代改进， Gooding 方法与测距迭代方法的主要不同在于，前者采用三个时刻之间的时间差（即Δt12和 Δt32） 作为目标函数，后者通过t1和t3时刻假设的测距信息计算t2时刻目标相对于测站的位置矢量，该矢量在与t2时刻望远镜视准线垂直的平面上的投影即为目标函数[17]。Laplace 法、Gauss 法和Gooding 法的数学模型及公式推导过程可以参考文献[6]和[14]。

在上述方法的基础上，文献[18]提出了距离搜索法，其实现过程如下。假设在t1,t2,...,tn时刻分别获得某空间目标的角度观测值赤经αi(i=1,2,3,...,n)和 赤纬δi(i=1,2,3,...,n)。测站到空间目标方向（即望远镜视线方向）的单位矢量Li(i=1,2,...,n)可以表示为Lxi,Lyi,Lzi分 别为Li在天球坐标系下三个方向的分量。利用ρ1和ρn表 示t1和tn时刻的观测距离，如果已知ρ1和ρn， 即可根据ri=Ri+ρiLi(i=1,n)得到两个位置矢量r1和rn，这样纯角度的初轨确定问题转换为基于两个位置矢量的轨道确定问题，即初轨确定Lambert 问题。可以在一定区间内以一定步长分别假设ρ1和ρn的值，这样每一个观测值组合可以算出一组轨道参数，基于此参数可以计算其他时刻的角度观测值，并与实际观测值进行比较。根据残差进行判断，筛选出可能的定轨结果，进而根据半长轴和偏心率等约束可筛选出最优解。

2 地基监测LEO 目标

2.1 仿真地基监测LEO 目标数据

设定光学望远镜参数并仿真产生LEO 目标监测数据。设定光学监测站地心地固系坐标，光学望远镜视场为6°×6°。仿真时间为2014 年11 月15－16 日。仿真产生空间目标轨道，根据可见性条件[20,21]仿真产生角度观测数据[22]，得到120 个目标的观测数据，采样频率为1 Hz。目标的轨道分布如图1 所示。

图1 仿真观测LEO 目标轨道近地点高度与偏心率分布Fig. 1 Orbit distributions of LEO objects for generating simulated observations

这些观测数据弧长均大于10 s，但在实际计算时会根据要求截取弧段的前30 s 或者60 s。基于仿真角度数据，添加不同的观测误差，进行初轨确定，分析观测值角度误差对定轨的影响。初轨计算结果分别列于表1 和表2。

根据表1 和表2，在最理想的情况下（角度误差为零时），Gauss 方法的初轨确定成功率非常高，同时半长轴的误差也较小（50 km）。随着角度误差增大，初轨确定成功率下降并且初轨误差显著增大，当角度误差为5＂时，半长轴误差达到1500 km（见表2）。对比这三种方法可以发现，Laplace 方法的成功率最低；当角度误差很小（≤0.5＂）时，Gauss 方法误差最小，成功率也较高。对比表1 和表2 可知，同等误差条件下，随着观测数据弧长增大，Gauss 方法和Gooding 方法初轨误差显著降低，而Laplace 方法初轨误差变化不大。

表1 仿真地基监测LEO 目标10～30 s 弧长数据初轨结果Table 1 IOD results of the arcs with length ranging from 10～30 s of LEO objects with ground-based observations

表2 仿真地基监测LEO 目标30～60 s 弧长数据初轨结果Table 2 IOD results of the arcs with length ranging from 30～60 s of LEO objects with ground-based observations

2.2 地基实测LEO 目标数据

采用中国科学院国家天文台长春人造卫星观测站的角度观测数据进行计算。长春人造卫星观测站光电阵由8 台口径15 cm、焦距15 cm 的光学望远镜组成，每台望远镜配置1 台分辨率为3000 pixel×3000 pixel 的CCD。此外还配置了8 台图像处理计算机，1 台GPS 时钟，电控系统，图像采集与处理系统等。光电阵监视天区高达1590 平方度，主要观测0.5～1 m 的空间碎片，角度误差为9＂，角度数据时间间隔约1.7 s[23]。该设备主要用于空间碎片的观测和研究。

利用其2017 年8 月24－26 日的观测数据，结合TLE 目标编目库数据，通过关联找出已编目TLE 目标的数据。合并重复目标后统计发现，所选三天时间内共观测到1960 个空间目标，观测一次和两次目标的数量分别为529 和319，占比为27%和16%（见表3）。

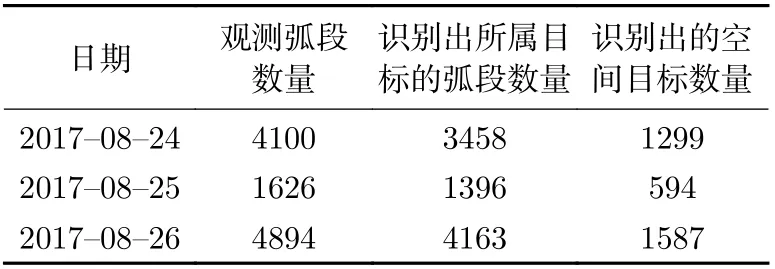
表3 识别出的空间目标和观测弧段数量Table 3 Number of the identified space objects and the arcs

利用已知目标的观测弧段，对初轨确定方法进行测试，并对初轨结果进行分析。图2 给出了观测数据弧长分布，可以看出弧长小于30 s 的弧段占比约为40%，小于60 s 的弧段占比约为70%，即大多数都属于甚短弧光学弧段。图3 给出了地基光电阵观测到的目标轨道分布情况。根据图3 可知，观测到的目标大部分是LEO 目标，轨道高度在2000 km 以下，倾角大部分位于60°～105°。

图2 空间目标观测弧段数目和观测数据弧长累计分布Fig. 2 Arc number of the space objects and the accumulated ratio of the arcs with different length

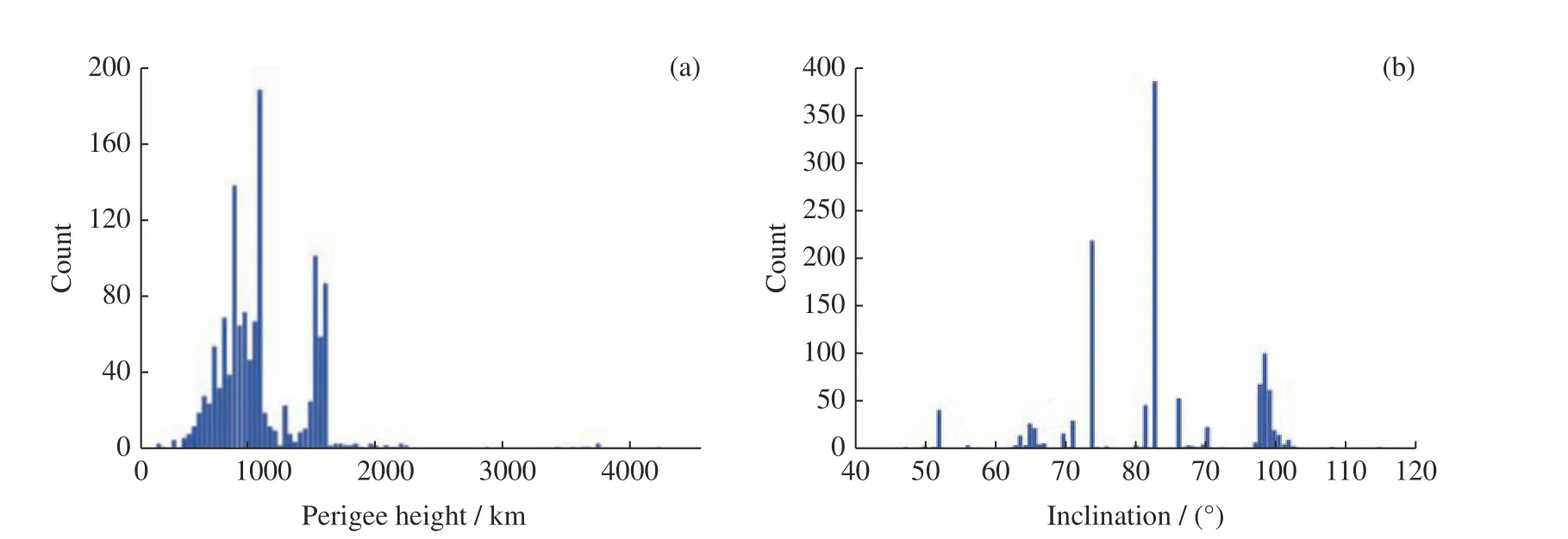
图3 地基光电阵观测到的目标轨道参数分布（近地点高度、倾角与空间目标数量）Fig. 3 Distribution of the orbit elements of the space objects obtained by the ground-based EO array (Altitude of the perigee，inclination and the number of space objects)

利用2017 年8 月24 日长春光电阵的角度数据，通过截取不同长度的观测数据，进行不同方法的初轨确定试验，分析观测弧段弧长对定轨结果的影响（见表4）。由表4 可知，四种算法的整体表现与表1 和表2相似。具体而言，对长春光电阵角度数据进行初轨确定，距离搜索法成功率较高，并且误差较小，Laplace 方法成功率最低；无论采用哪种方法，初轨误差均较大，这可能是由于角度误差太大引起的。另外，当观测数据弧长从10～30 s 变为30～60 s 时，四种方法的初轨成功率显著提高，采用Laplace 方法和Gooding 方法时初轨误差基本不变，但采用Gauss 方法时，初轨误差显著降低。总体而言，距离搜索算法表现最好，轨道计算成功率最高并且误差最小。以上结果说明，距离搜索算法适用于实测地基甚短弧角度数据的定轨。

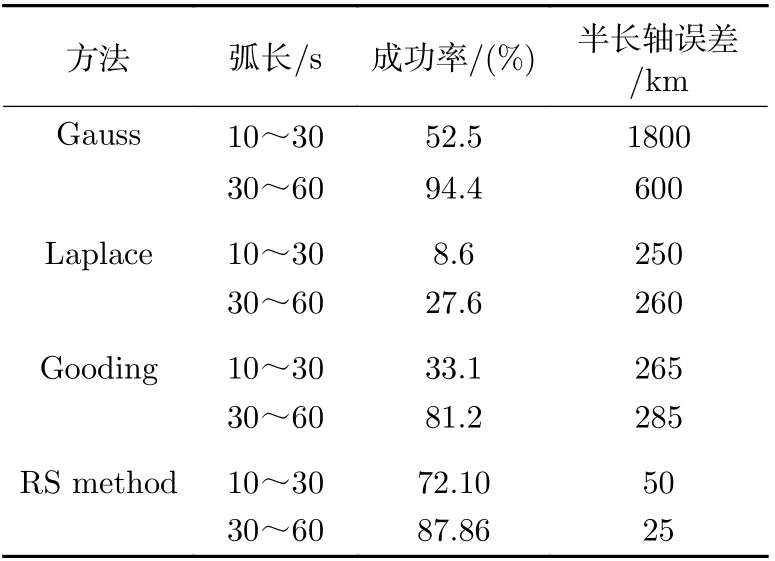
表4 地基光电阵监测LEO 目标观测数据初轨结果Table 4 IOD results of space objects observed by the ground-based EO array

2.3 仿真天基监测数据

设定天基监测卫星的轨道为圆轨道，轨道高度为610 km，轨道倾角约64.5°，望远镜指向监测卫星轨道面的法向方向，观测频率10 Hz。在TLE 目标编目库中，随机选取部分轨道高度＜5000 km、偏心率＜0.01的空间碎片，仿真角度观测数据。首先，产生观测平台和空间碎片在2015 年1 月16－19 日的“真轨道”[19]，然后反算观测目标的角度观测数据（赤经和赤纬）。选取720 个目标的首个弧段进行初轨确定试验。弧段长度大部分为10～20 s，其中146 个观测弧段弧长＜10 s，利用≥10 s 的574 个弧段进行试验。由于Laplace 方法的成功率基本为零，因此表5 和表6 给出了利用另外两种方法进行初轨确定的结果。

由表5 可以看出，用Gauss 方法进行初轨确定，当观测数据弧长位于10～30 s 时，与地基观测数据相比，天基数据的初轨成功率显著降低，并且天基数据初轨误差显著大于地基数据初轨误差，这可能是由于天基数据平均弧长小于地基观测数据导致的。比较表5 和表6 可知，弧长增大，初轨误差显著降低。例如，当角度误差为10＂，弧长位于10～30 s 时，初轨半长轴误差达到4000 km，而当弧长位于30 ～60 s时，半长轴误差降为800 km。根据Gooding 方法的结果，地基监测数据也整体优于天基监测数据。总体而言，随着角度误差增大，Gauss 方法和Laplace 方法初轨确定成功率迅速下降，并且初轨误差急剧增大；Gooding 方法初轨结果受角度误差的影响不是很大，并且增加弧长可显著降低初轨误差。

表5 仿真天基监测LEO 目标10～30 s 弧长数据初轨确定结果Table 5 IOD results of the arcs with length ranging in 10～30 s of LEO objects with space-based observations

表6 仿真天基监测LEO 目标30～60 s 弧长数据初轨确定结果Table 6 IOD results of the arcs with length ranging in 30～60 s of LEO objects with space-based observations

3 结论

初轨确定是进行空间目标编目的关键环节，本文利用地基光电阵实测角度数据和仿真天基、地基光学监测LEO 目标的角度观测数据，进行了初轨确定的常用算法比较。为进行详细的算法测试，将观测数据按照弧长分为10～30 s 和30～60 s 两组，角度误差分为0＂, 0.5＂, 5＂, 10＂四组进行分析。结果表明，在初轨确定成功率和初轨参数误差两个方面，距离搜索算法表现最好，其次为Gooding 方法。初轨确定成功率和初轨误差受弧长和角度误差的共同影响，弧长越长，误差越小，而初轨成功率越高，初轨参数误差越小。当误差很小 (＜1＂) 时，可以考虑采用Gauss 方法，误差较大时可以考虑采用距离搜索算法。总体而言，甚短弧角度观测数据条件下距离搜索算法在解算成功率和初轨误差两方面均表现优异，适用于LEO目标初轨确定，具有较大的应用潜力。