基于NSGA-Ⅲ算法的区域水资源优化配置研究

侯 岳， 李治军， 黄佳俊， 王华凡

（黑龙江大学水利电力学院，哈尔滨 150000）

水是人类生存发展的重要资源，随着城市化进程加快，城市用水需求、农田灌溉用水量不断增加，目前水资源短缺、各用水部门分配水量不协调、水资源供需矛盾等问题已严重影响到社会经济的可持续发展［1-2］，特别是水资源相对匮乏、农业用水较大的地区水资源系统面临着极大的挑战，因此为水资源合理配置和持续利用提供指导尤为重要.

近年来，水资源优化配置研究已得到越来越多的国内外学者重视，并在多个方面取得进展. Noori 等［3］采用遗传算法、合作博弈论和ABM三种主要方法对塔江流域进行水资源优化配置，为水资源需求管理和最佳水量分配创造一个水文-环境-人类关系；Kutty和Hanumanthappa［4］以孟加拉国鲁市为例利用数据挖掘技术对国内用水部门进行水资源优化配置构建体系结构模型；吴云等［5］以汾河下游谷地供水区为例，采用改进飞蛾扑火算法寻优结果对所构建的研究区进行水资源优化配置；杜佰林和杨丹［6］以县作为研究区，以社会、经济、生态效益为目标建立模拟退火粒子群优化配置模型，对不同规划年进行水资源优化配置；田林钢和杨丹［7］基于鲸鱼优化算法对县级研究区规划年的水资源进行优化配置. 综合国内外研究成果，NSGA-Ⅲ算法大多应用于车间或水库调度问题的研究［8-9］，水资源优化配置应用较少，目前水资源优化配置的研究较多，其中以县为单位针对农业用水量较大的市级作为研究区的水资源优化配置研究较少. 鉴于此，本文选取三江平原的佳木斯市为例，基于社会-经济-生态环境效益目标构建水资源多目标优化配置模型，以2020年为现状年，2030年为规划年，利用NSGA-Ⅲ算法求解pareto最优解集，利用目标函数的侧重点不同，得到规划年佳木斯市各子区域各用水部门的四种水资源配置方案，对四种方案进行对比，得出最优方案为水资源优化配置提供科学依据，保障水资源系统与区域社会经济发展相协调.

1 NSGA-Ⅲ算法

NSGA-Ⅲ算法是Deb和Jain［10］在NSGA-Ⅱ算法的基础上改进而来的，该算法基于参考点机制对种群个体进行选择，取代了NSGA-Ⅱ算法中拥挤度和拥挤度比较算子的计算，采用参考点引导种群搜索方向，提高种群的多样性，并且pareto解在非支配层上分布较为均匀，有效提升了算法的收敛性，具体算法流程描述如下.

1）生成新种群. 首先在随机化过程中产生一组规模为N的父代种群Pt，用遗传算子（选择、重组、变异）对父代种群进行操作，生成一组规模为N的子代种群Qt，再将父代种群Pt与子代种群Qt组合（Pt∪Qt），得到一组规模为2N的种群Rt. 再将种群Rt通过非支配排序分为多个非支配层，把每个支配层的个体依次加入下一代子代集合D，当集合D的规模大于N时，在该非支配层级下挑选种群规模为N的一组个体，生成新的种群St.

2）参考点设置. 在标准化超平面上，按照公式（1）均匀产生参考点，其参考点在（M-1）维的超平面上，M为目标函数个数，如果将每个目标分为S份，即其参考点R的数量为：

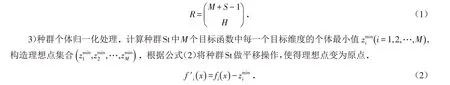
计算每个目标函数的极值点，具体公式如式（3）所示：

式中：δ为坐标轴的单位方向向量，当δi=0时，则取10-6.

根据各个坐标轴的极值点与其理想点组成的直线构造M维的线性超平面，该面与坐标轴的焦点即为截距αi，通过线性超平面通用方程，代入具体函数值求出截距，利用截距按照公式（4）进行归一化处理.

4）输出配置方案. 原点与参考点的连线作为参考线，计算种群St中个体到各参考线的距离，个体与参考线距离最近建立关联关系，利用参考点最优策略机制选择靠近参考点规模为N的一组个体加入下一代种群中，算法迭代往复进行，直至达到收敛条件.

NSGA-Ⅲ算法流程见图1.

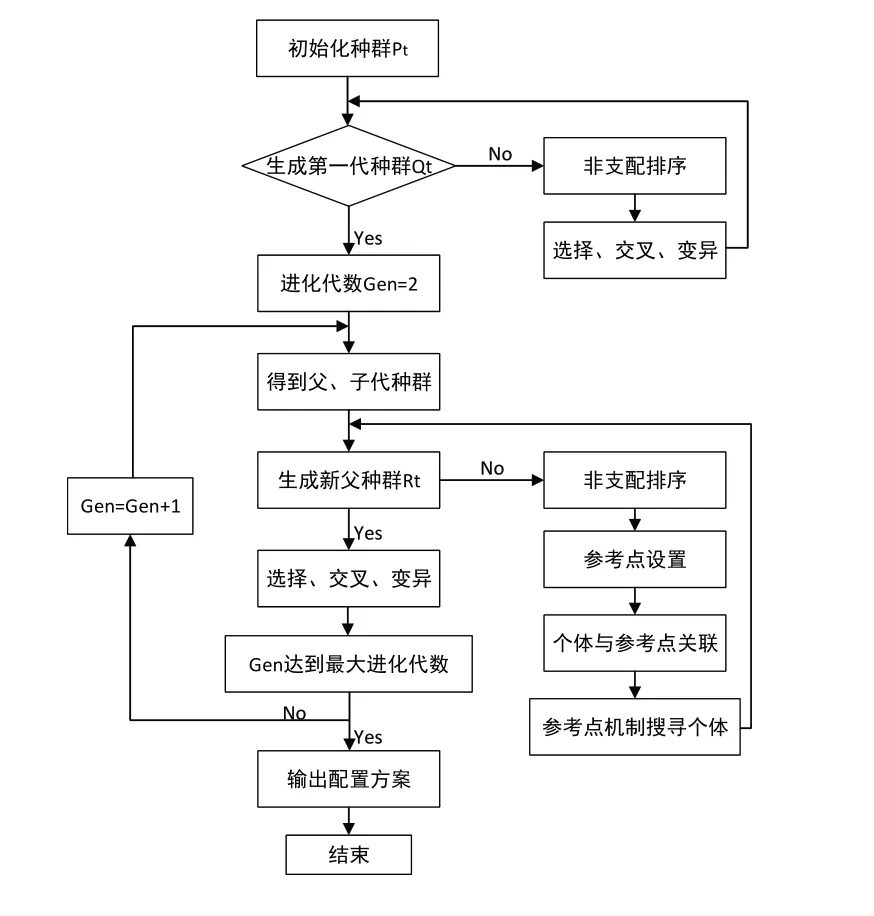
图1 NSGA-Ⅲ算法流程Fig.1 NSGA-Ⅲalgorithm flow

2 实例分析

2.1 研究区概况

佳木斯市位于黑龙江省东北部，地处三江平原腹地，属中温带大陆性季风气候，多年平均降雨量553 mm，降雨量时空分布较为不均. 由于该市为我国重要商品粮基地和三江平原重点开发区，农业部门用水较大，水资源开发程度较高，截至2020年，已严重超过当地的水资源开发利用控制指标，这也将导致水资源供需不平衡、各部门用水不协调等系列问题日益突出. 因此，对佳木斯市进行水资源优化配置，以有效缓解水资源供需矛盾、提高供水效率，实现各用水部门科学合理化配置.

2.2 水资源优化配置模型构建

2.2.1 目标函数1）社会效益目标. 在满足各用水部门的用水需求的基础上，以研究区水资源缺水量最小为社会效益目标.

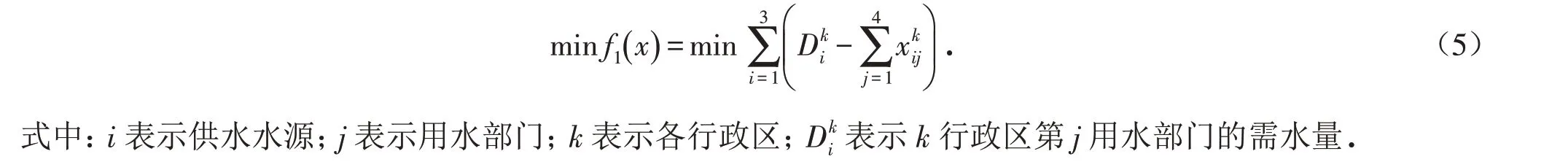
2）经济效益目标. 在以经济可持续发展为前提下，区域各用水部门需水所带来的经济效益最大为经济效益目标.

2.2.2 约束条件

1）供水能力约束：

4）变量非负约束：

2.2.3 模型参数的确定

1）供水次序与需水公平系数. 供水次序系数表示各水源供水的优先程度；用户公平系数表示各用水部门得到供水的优先程度，与供水次序系数相似，与用户优先得到供水的次序有关，参考公式如下：

式中：ni表示k子区的i水源的供水次序序号；nmax表示k子区水源供水次序最大值.

根据公式计算求得地表水、地下水及非常规水源的供水次序系数分别为：0.5、0.33、0.17；各用水部门的用水公平系数分别为：生活用水0.33、生态环境用水0.27、第三产业用水0.2、工业用水0.13、农业用水0.07.

2）用水效益系数与用水费用系数. 工业、第三产业用水效益系数通常由部门工业增加值用水量与第三产业增加值用水量的倒数确定，农业用水量由单位面积农业灌溉效益与农业灌溉定额的比值确定，根据该区域社会经济发展状况，确定生活用水、生态环境用水效益系数取300元/m3，工业用水取45元/m3，第三产业用水取8元/m3，农业用水取14元/m3；以2020现状年供水价格为标准确定用水费用系数，居民生活用水为2.8元/m3，农业用水为0.16元/m3，工业用水为2.7元/m3，第三产业用水为2.5元/m3，生态环境用水为1.5元/m3.

3）污水中COD 排放浓度与污水排放系数. 根据研究区相关资料，确定该区域的污水排放中化学需氧量（COD）为60 mg/L，故以此作为规划年的污水中COD 排放浓度. 本文只考虑生活和工业污水的排放，其规划年生活污水排放系数为0.75，工业污水排放系数为0.55.

2.3 供需水量预测

研究区需水量预测是水资源优化配置的基础，主要包括居民生活、农业、工业、第三产业及生态环境用水量，常用的方法有定额法、时间序列法、多元线性回归、神经网络法等，本文采用定额法选取2020年为现状水平年，以2030年为规划年对各部门需水进行预测. 规划年供水量根据研究区用水总量控制方案、水资源规划确定，规划年佳木斯市各水源地可供水量与各用水部门需水量预测结果见表1.

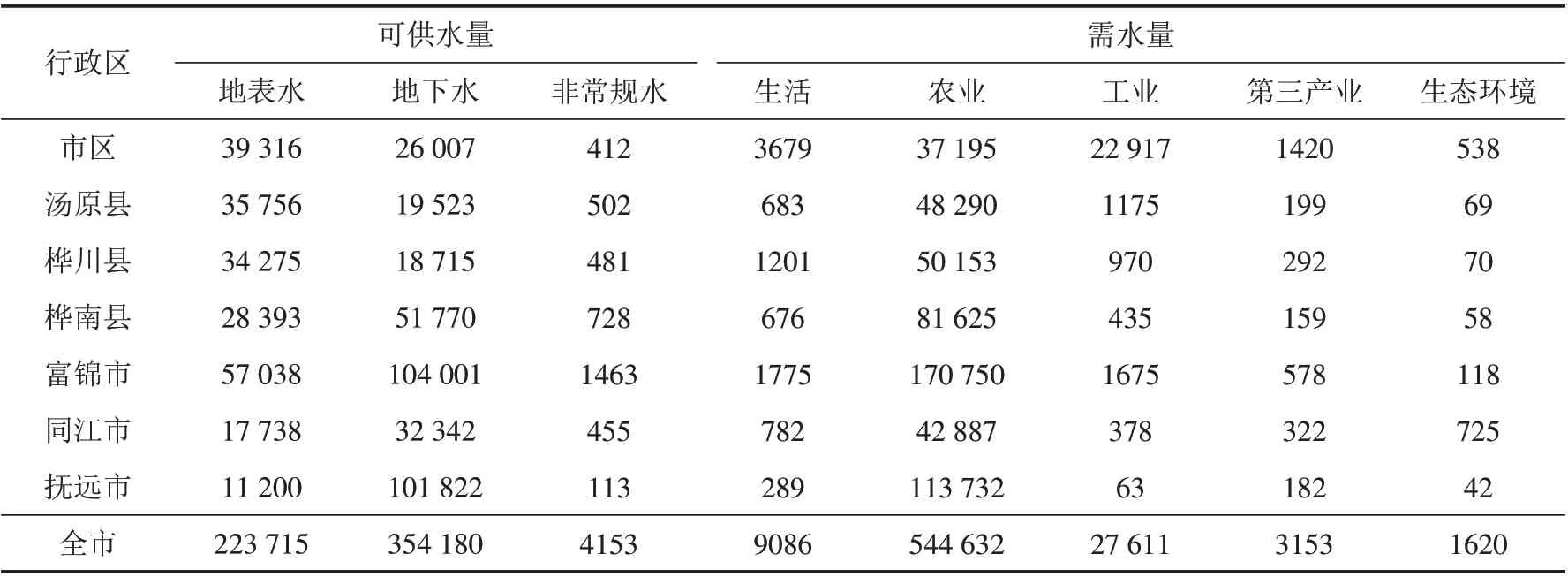
表1 2030年佳木斯市供需水量预测结果Tab.1 Forecast results of water supply and demand of Jiamusi in 2030单位：万m3

3 模型运行结果分析

在佳木斯市规划年水资源优化配置与调度中，主要包括三个目标函数，分别是社会、经济、生态环境效益目标. 因此，本文以每个目标分别为侧重点，利用Delphi法［11］设定每个目标函数的权重，使每个目标函数达到最优化配置，主要提出以下四种不同优化配置方案：方案一约束条件不变，优先考虑社会效益目标，经济效益目标与生态环境效益目标权重分别为0.55和0.45；方案二约束条件不变，优先考虑经济效益目标，社会效益目标与生态环境效益目标权重分别为0.55 和0.45；方案三约束条件不变，优先考虑生态环境效益目标，社会效益目标与经济效益目标权重分别为0.55和0.45；方案四约束条件不变，综合考虑3个目标函数，使社会、经济和生态环境协同发展.

采用NSGA-Ⅲ中pareto最优解求解上述四种不同配置方案，设置种群数N=300，进化迭代500次，分别求得研究区规划水平年2030年佳木斯市水资源优化配置方案，具体见表（2）～（5）.

表2 各用水部门水资源优化配置方案一Tab.2 Optimal allocation option 1 of water resources in each water-using sector单位：万m3

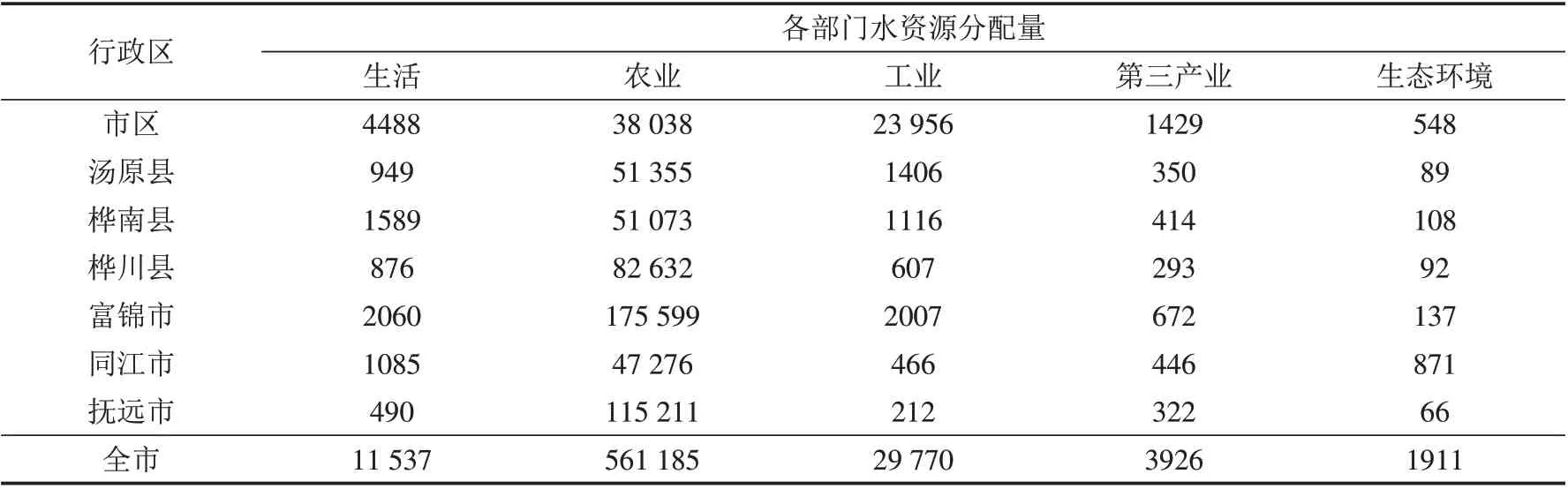
表3 各用水部门水资源优化配置方案二Tab.3 Optimal allocation option 2 of water resources in each water-using sector单位：万m3

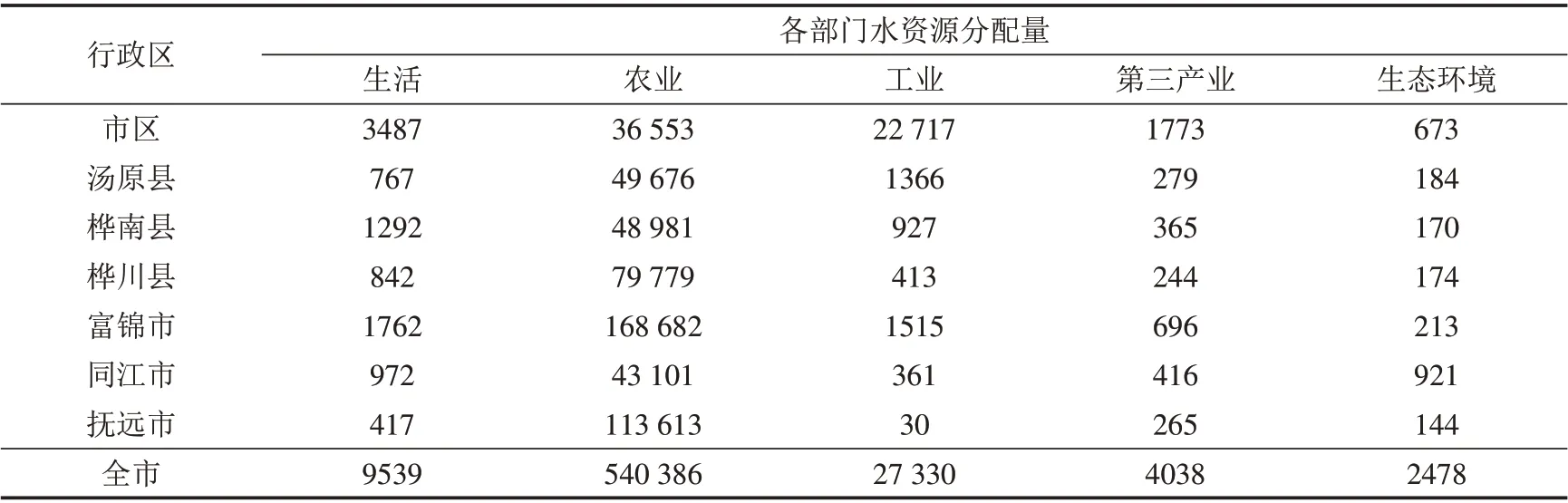
表4 各用水部门水资源优化配置方案三Tab.4 Optimal allocation option 3 of water resources in each water-using sector单位：万m3

表5 各用水部门水资源优化配置方案四Tab.5 Optimal allocation option 4 of water resources in each water-using sector单位：万m3

根据不同侧重点，制定四种水资源优化配置方案：方案一，社会效益目标可供水量盈余819万m3，经济效益目标为642 737万元，生态环境效益目标COD排放量22 101 t，配水总量为581 229.4万m3；方案二，社会效益目标缺水量为26 281.4万m3，经济效益目标为69731万元，生态环境效益目标COD排放量28 220 t，配水总量为608 330.4万m3；方案三，社会效益目标缺水量为1720.5万m3，经济效益目标为580039万元，生态环境效益目标COD排放量7 911.1 t，配水总量为583 769.5万m3；方案四，社会效益目标缺水量为109.7万m3，经济效益目标为672 065万元，生态环境效益目标COD排放量22 090 t，配水总量为581 939.3万m3.

综上四种水资源优化配置方案可知，方案一为了降低全市的缺水程度，从而减小了各用水部门的需水量，但未充分考虑区域的经济效益，使其经济效益目标值是四种方案中最低；方案二侧重于经济效益，生活、农业、工业及第三产业的用水量大幅度提升，导致缺水率严重、污染物排放量较大的情况；方案三侧重于生态环境的保护，增大第三产业与生态环境的用水量，降低了污染物的排放量，但经济效益同样较低，未能满足区域的经济发展；方案四侧重于社会、经济、生态环境三方面协调发展，保证在满足生活用水的前提下，调整用水结构，加大第三产业、生态环境用水量，既注重社会经济发展，又考虑到生态环境的保护与管理，整体水量配置符合社会经济、生态环境的可持续发展. 因此方案四可推荐作为研究区水资源优化配置的最优方案，为决策者提供参考依据. 方案四社会-经济-生态环境效益目标pareto最优解见图2.

图2 社会-经济-生态环境效益pareto最优解集（方案四）Fig.2 Pareto optimal solution set for the social-economic-ecological and environmental benefits（option 4）

4 结论

1）NSGA-Ⅲ算法利用参考机制提高了种群的多样性，在求解水资源多目标优化配置中，模型运行速度较快，pareto最优解收敛性较好，且优化结果精度较高，应用于水资源优化配置具有良好的表现，为日后解决类似研究提供新的方法.

2）根据目标函数的侧重点不同，共求得四种水资源优化配置方案，其中方案一水资源缺水量最小，方案二经济效益最大，方案三化学需氧量排放量最小，方案四社会、经济、生态环境效益较其他3个配置方案较为适中，基本满足规划年用水需求，可作为最优方案，为研究区水资源科学合理配置提供参考依据.