基于水流冲击响应的桥墩冲刷识别方法研究

陈旭辉， 唐永圣， 梅 曦， 沈国根

（1.河海大学土木与交通学院，南京 210098； 2.江苏华通工程检测有限公司，南京 210014；3.扬州市隧道管理处，江苏扬州 225100）

桥墩冲刷是指水流经过桥墩周围会裹挟桥墩周围部分土壤，从而使桥墩周围形成坑洞. 河流的冲刷作用使泥土对桥墩的约束减弱，常常导致其承载力下降，发生倾斜变形甚至失稳破坏. 刘亢等［1］统计了2007—2015年全国因洪水导致的桥梁垮塌数量，发现其中超过半数均是桥墩冲刷导致的失稳破坏. 因此研究桥墩冲刷监测或快速检测方法有助于及时发布桥梁危险预警和构建桥梁安全体系，具有重要意义.

目前，用于桥墩冲刷测量的方法主要有人工检测法、探地雷达法、声呐法和光纤传感器法等. 熊文等［2］在综述中提及，如今桥梁冲刷检测最为广泛应用的仍是水下潜水员技术，该方法直观准确，但成本高昂且存在安全风险；Anderson等［3］使用探地雷达对美国密苏里州的10座桥进行了冲刷检测，通过发射和接受电磁信号可获得河床形状信息，继而判断桥墩冲刷情况，但该方法在水深10 m以上的河流中不适用且不能用于海水中. 声呐扫面技术也常用来实施冲刷监测，该方法可以检测冲刷坑深度，精度可达厘米级，还可以建立河床深度的连续剖面，但容易受到湍流的干扰［4-5］. 分布式光纤技术因其优良的动静态传感性能，也被用于冲刷监测的研究，主要通过测量传感器的应变时程变化来确定冲刷状况，但该技术需要将传感器长期布置在水中，可能面临长期性能不足的问题［6-7］.

冲刷会导致桥墩埋深减小、墩身自由段长度增加，进而导致侧向刚度降低，其固有频率也会相应减小.因此，通过测量桥墩固有频率来实现桥墩冲刷状况监测具有可行性［8-10］. 在实际工程中，一般采用加速度计测量结构的固有频率，可将加速度计安装在桥墩水上部分，具有安装方便、长期性能好、灵敏度高、成本低等优势，可以满足快速检测或长期监测的需要，应用前景广阔.

针对上述问题和所提的研究思路，本文展开理论和试验研究. 首先，基于经典振动方程，推导桥墩固有频率与桥墩自由段长度的理论关系；然后，基于桩土的等效嵌固理论，提出桥墩自由段长度的修正方法，进而提出桥墩冲刷后自由长度的计算方法；最后，利用有限元模型和现场实桥试验对本文所提方法进行验证.

1 桥墩冲刷识别理论和方法

1.1 桥墩冲刷模型和计算方法

对于桥梁中常见的摩擦摆支座［11］及盆式橡胶支座［12］，其允许上部结构与桥墩之间产生一定的横向相对滑移，上部结构为桥墩提供的水平向约束较弱，所以在桥墩水流冲刷的力学简化模型中，可以将桥墩视为一端固接、一端弹簧支座的欧拉梁. 但是在实际中支座的弹簧系数难以测量，为此本文偏于安全考虑（从测量评估角度），忽略上部结构对桥墩的横向约束，力学模型简化为受轴压力的悬臂欧拉梁. 图1中Le为桥墩自由段理论长度；EI为桥墩的抗弯刚度；N为桥墩顶部轴压力（即上部结构的自重）. 对于解析桥墩的固有频率，其轴向压力对结果有影响，因此在模型中包含了轴力而忽略了其他水平荷载.

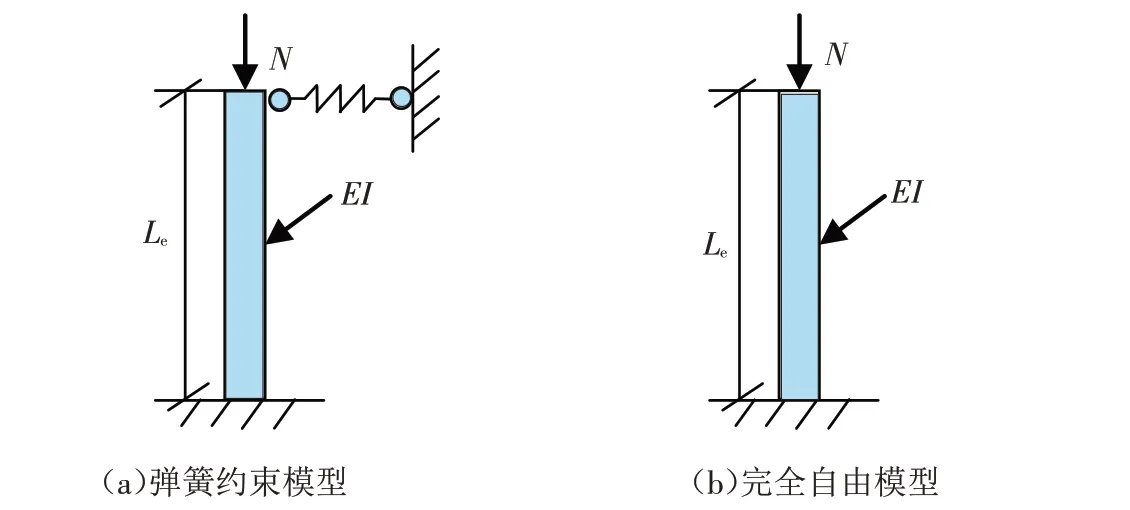
图1 桥梁支座及桥墩简化模型Fig.1 Simplified model of bridge support and bridge pier

本文研究对象为上部横向约束作用较弱的等截面桥墩，对于变截面等其他类型桥墩，可对理论公式进行修正，本文不再推导相关公式.

由振动力学相关知识［13］可知，不考虑剪切变形和转动惯性的悬臂梁运动微分方程为：

其中：y(x,t)为距离固定端x处的点在t时刻的横向位移；A为横截面面积；ρ为材料质量密度.

将方程的解分离变量为ϕ(x)q(t)，并带入式（1）得到

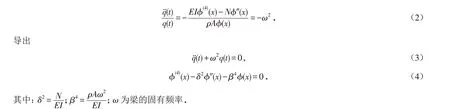
利用指数形式特解ϕ(x)=eλx代入式（4），导出本征方程

基于本征方程，可以解得式（4）的通解如式（6）所示：

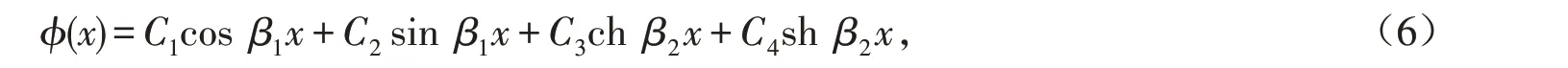
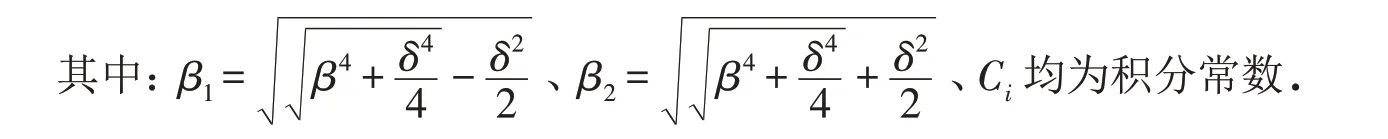
根据悬臂梁的边界条件，得到频率方程

已知ω=2πf，利用文献［14］中的方法解出上述方程的近似解，得到完全自由模型的桥墩长度与固有频率相关方程：

1.2 桥墩计算长度修正

上述理论长度Le并未考虑桥墩与土体的动力相互作用［15］，忽略了约束作用较弱的表层浮土，为了与实际相符，需对Le进行修正. 本文引用等效嵌固模型来考虑墩土动力相互作用，将桥墩底到最大冲刷线下某一位置（等效嵌固点）的墩土进行固定，忽略等效嵌固点以上的土体约束（如图2）. 该方法可将墩土动力相互作用转化成简单的静力问题，且能保证一定的工程精度［16］. 将理论长度Le扣除等效嵌固深度t后即为桥墩自由段长度L，该自由段长度L与现有监测方法相符，因此可相互印证比较.

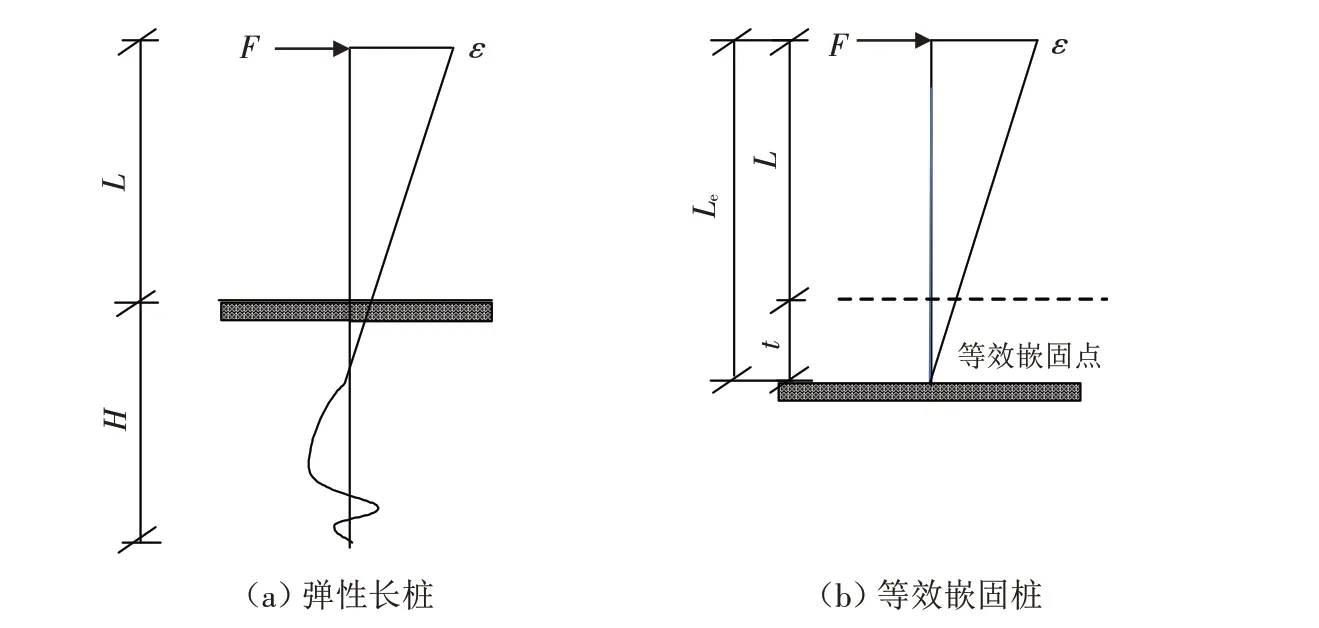
图2 弹性长桩与等效嵌固桩Fig.2 Elastic long pile and equivalent embedded pile

本文采用国际《码头结构设计规范》（JTS 167—2018）中求解等效嵌固点深度的方法，计算公式如下所示：

式中：Le为桥墩自由段理论长度；L为桥墩自由段修正长度；t为等效固结深度；k为群桩效应系数，不考虑群桩效应时取1.0；kf为形状换算系数，圆形墩取0.9，矩形墩取1.0；d为桥墩直径或垂直于水平力方向的墩宽（m）；b0为桥墩的换算宽度（m）；η为系数，取值为1.8～2.2之间，当上部结构约束较弱时取较小值，较强时取较大值；m为土的水平抗力系数；EI为桥墩的抗弯刚度.

2 桥墩冲刷识别的数值模拟研究

2.1 有限元模型概况

本文选取某跨河实桥简化模型进行数值模拟研究，如图3所示. 桥面板及桥墩均为钢筋混凝土结构，混凝土等级为C50. 桥面板采用实腹梁形式，截面尺寸为11.35 m×1 m，共三跨，每跨长40 m；桥墩为重力式矩形桥墩，截面尺寸为7.25 m×2.3 m，总高36 m，初始埋深26 m，水深6 m.

图3 桥梁有限元模型Fig.3 Finite element model of bridge

通过ABAQUS 软件建立该有限元模型，桥面板和桥墩均采用B33 梁单元（可受轴向压力）；支座通过Planar Connector进行模拟，该连接器使桥面板对桥墩无横向位移约束且能传递竖向荷载. 土的水平抗力系数m取30 000 kPa/m2，在ABAQUS中通过接地弹簧模拟地基土对桥墩的约束作用.

以左侧第二个桥墩为冲刷模拟对象，选取未冲刷及冲刷深度分别为0.5、1、2 m共四种工况. 在ABAQUS中采用集中周期荷载模拟波浪荷载，作用位置为桥墩水面处节点，荷载时程曲线通过Morison方程计算获得［17］，荷载周期均为9 s，波高均为0.6 m. 在河道汛期和非汛期，作用于桥墩的水流作用差异较大. 为考察该方法在不同水流状况下的稳定性，选取冲刷深度1 m 作为典型工况，分别设置0.1、0.6、1.2 m三种不同波高的波浪荷载，波浪荷载时程曲线如图4所示.

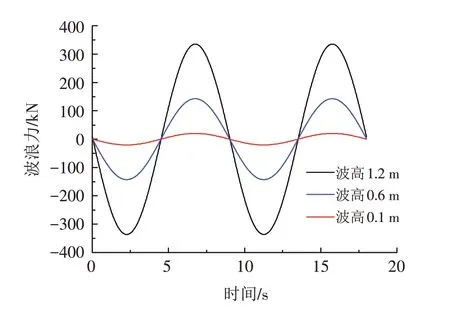
图4 典型工况（冲刷深度1 m）下波浪荷载时程曲线Fig.4 Time-history curve of wave load under typical working condition（scour depth 1m）

2.2 模拟结果与分析

本文提取左侧第二个桥墩某一节点（距水面距离为2.5 m）在不同工况下的加速度时程曲线，并将其进行傅里叶变换后获得相应的频谱，得到桥墩的一阶弯曲振动模态，继而判断桥墩的固有频率. 以典型工况为例，不同波浪荷载下的加速度时程曲线如图5（a～c）所示，相应的频谱图如图5（d～f）所示，图中所标信息即为该桥墩的固有频率. 从图中可以发现该方法在不同水流状况下具有较高的稳定性，通过计算获得的固有频率均趋于一个固定值，与理论预期相符.

图5 典型工况（冲刷深度1 m）下加速度时程曲线及频谱图Fig.5 Acceleration time-history curve and frequency spectrum under typical working condition（scour depth 1 m）

将所有工况提取得到的固有频率代入公式（8～12），即可得到桥墩在该冲刷状况下的自由段长度L. 表1给出了所有工况下的计算自由墩长与实际自由墩长. 由表1结果可知，本方法在有限元模型中的识别误差在6%以内，精度较高；此外，计算自由墩长均大于实际自由墩长，说明该方法所得数据偏于保守，符合工程检测需求.

表1 有限元模型桥墩冲刷识别结果Tab.1 Identification results of bridge pier scour in finite element model

3 桥墩冲刷识别的实桥试验研究

3.1 试验概况

为验证该方法在实际水流冲击作用下的适用性，选择位于长江边的某人造观景台桩基作为试验对象进行现场试验. 本试验所用仪器包括带有磁性端头的加速度传感器及TST3827E 动静态信号测试分析仪，如图6所示. 上部结构对该桥墩的横向约束作用较弱，桥墩自由段长度为1.39 m，直径为0.3 m. 激励方式分为人工锤击激励和水流冲击激励. 为保证数据质量，人工锤击位置离江面5 cm，锤击次数不少于20次. 在进行水流激励时，为保证获得有效的水流冲击，试验选择潮汐时间，数据采集持续3 h以上.

图6 实桥试验概况Fig.6 Overview of real bridge test

3.2 试验结果和分析

将加速度传感器采集到的数据先利用随机减量法［18-19］进行处理，处理后的加速度时程曲线及频谱图如图7所示. 从图7（a）和（c）中可以看出水流冲击下的加速度信号与锤击相比有较大区别，但图7（b）和（d）所示两者所得固有频率相近，因此可以认为两种激励方式对桥墩的影响相似. 将采集的频率进行汇总，所得频率都趋于一个特定值，故本文取平均值作为该桥墩的固有频率，分别为15.84 Hz（人工锤击）和15.38 Hz（水流激励）. 利用公式（3～7）对本试验取得的频率结果进行计算得表2.

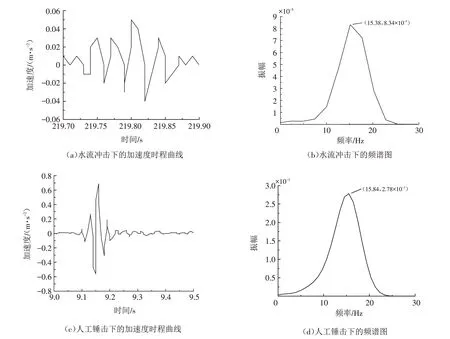
图7 不同激励下的典型加速度时程曲线及频谱图Fig.7 Typical acceleration time-history curves and frequency spectra under different excitations

从表2 可以发现，人工锤击和水流冲击两种方法所得计算自由墩长均略大于实际自由墩长，误差控制在10%左右，具有良好的工程精度. 该误差产生的原因分析如下：①该桥墩并不是理论上的悬臂梁，其上部结构对桥墩有一定的横向约束；②土的水平抗力系数m为经验取值，与实际存在偏差. 通过实桥试验证明，本方法对桥墩冲刷进行长期监测具有可行性，在保证一定精度的条件下能进行快速稳定识别.

表2 实桥试验桥墩墩长识别结果Tab.2 Identification results of bridge pier length in real bridge test

4 结论

针对桥梁冲刷监测难的问题，本文提出了利用水流冲击产生的加速度响应识别桥墩冲刷的方法，建立了桥墩自由段长度计算方法. 通过理论和试验研究，本文可得到以下结论.

1）通过测量桥墩固有频率可实现桥墩冲刷量化评估. 本文建立了桥墩频率和桥墩自由段长度的解析公式，并进一步考虑了桩土嵌固作用，提出了计算桥墩长度的修正方法，从而实现了冲刷的量化计算.

2）通过数值模拟试验，验证了所提方法的有效性和高精度. 利用水流作为环境激励，有限元模拟的结果表明，识别出的固有频率随着冲刷深度增加而减小，桥墩长度的计算误差小于6%；同时，不同等级波浪荷载对该方法没有显著影响，表明该方法适用性强.

3）通过实桥试验，进一步证明了本文所提方法可用于桥墩冲刷的精准监测，其中在水流冲击下桥墩长度计算误差约10%.

当然，本文的研究还存在不足，如不同土质、墩型等因素的影响还未考虑，实桥冲刷监测还未验证，将在后续展开相关研究. 本文所提方法具有传感装置简单、安装便利、灵敏度高、测量环境适用性强等优势，因此应用前景广阔.