基于EEMD-Attention-GRU的大坝变形组合预测模型

刘 俊， 王艳波， 崔旭廷， 曹德君， 贾玉豪

（1.南京市水利规划设计院股份有限公司，南京 210000； 2.河海大学水利水电学院，南京 210098；3.上海勘测设计研究院有限公司，上海 200335）

随着我国筑坝数量的不断增加，大坝变形性态分析备受关注. 及时获取变形观测数据、建立相应的分析模型以预报大坝行为，对大坝的稳定运行具有重大意义［1-2］. 由于水压、时效、温度等复杂环境因素的影响，大坝变形表现出非线性、非稳态的特性，这将使得传统分析方法很难准确反映自变量与因变量之间的复杂非线性关系［3-4］. 如何解决大坝变形非线性在分析过程中的负面影响是当前坝工领域内的热门主题.

随着智能算法的发展，一些学者摒弃传统的大坝变形分析方法，将BP神经网络、支持向量机等算法应用于大坝变形预测中［5-7］，利用统计模型提取出模型所需输入参数（水压、温度和时效）并作为输入样本融合到智能算法中，这在一定程度上提高了模型精度，但并不能从根本上解决变形的非线性问题. 随后，EMD［8］、EEMD［9］以及VMD［10］等信号处理算法被陆续应用到变形分析中，以降低数据的非线性和非稳定性，然后对分解得到的各个子序列分别建模，构建了大坝变形组合预测方法，有效提升了变形的预测精度.

然而变形不仅具有复杂的非线性，同时具有复杂的时序非线性. 近年来，随着计算机技术的大力发展，深度学习算法得以迅速发展并成为大坝变形预测的研究热点. 如郭张军等［11］将LSTM算法应用到大坝变形预测中；周兰庭等［12］基于小波分解、LSTM和Arima算法构建了混凝土坝变形组合预测模型；陈竹安等［13］利用VMD信号处理方法和LSTM算法构建了性能优越的大坝变形预测模型. 可以看出当前大坝变形预测领域的深度学习算法以LSTM为核心，涌现了许多不同的变形预测方法. LSTM算法解决了传统RNN的梯度消失、梯度爆炸等问题［14］，但其网络结构过于复杂，收敛速度较慢［15］. 门控循环单元（GRU）神经网络［16-17］在LSTM的基础上简化了神经网络的结构，具有更快的收敛速度. 不论是LSTM或者GRU都能够描述变形时序关系，但对于时序非线性较强的变形数据，二者均无法得到准确的非线性映射关系. 为此本文引入了Attention机制［18-19］的概念，该方法可以根据输入信息的重要性，在神经网络内部实施权重分配，从多步大坝变形输入信息中突出关键信息对变形预测结果的贡献度并传递给下一层，从而优化神经网络的时序非线性学习能力，达到预期的预测精度.

综上，本文提出了基于EEMD-Attention-GRU 的大坝变形组合预测模型. 首先通过EEMD 信号分解技术将原始数据分解为若干个频率不同的稳定分量；然后在GRU神经网络框架的基础上引入Attention 机制，在保持原始神经网络主体结构的同时，深入挖掘模型的时序非线性；最后组合各子序列对应Attention-GRU模型的预测结果，得到最终变形预测结果.

1 方法原理

1.1 EEMD

EMD算法具有自适应性、完备性和正交性三个优点，但也有其自身的缺点. 例如，EMD算法存在模态混淆现象，导致EMD分解得到的IMF分量缺乏物理意义. EEMD通过向原始信号中添加白噪声来改变极值点分布，从而消除了混杂效应，通过对EMD信号进行平滑处理，有效地解决了EMD信号的模态混淆问题. 对噪声进行多次平均，可以利用白噪声的零均值特性使噪声相互抵消，抑制甚至消除噪声的影响. EEMD具体的分解过程如下［20］：

1）在原始信号x(t)的基础上加上白噪声n(t)，从而形成新的信号y(t)：

2）使用EMD继续分解最新的时间序列y(t)：

其中ci表示第i个分解量；rn表示残差序列.

3）重复上述步骤，在每个时间序列具有相同振幅的新白噪声序列nj(t)添加到序列yj(t)：

其中j表示当前的循环数；cij表示yj(t)的第i个IMF分量；rjn表示yj(t)的残差序列.

1.2 GRU

GRU 是一种递归神经网络，它和基本RNN 的主要区别在于，RNN 的内存会随着数据序列的增加而减少，从而引起梯度消失的问题，GRU可以有效地改善这个问题. 同时，GRU也是一种简化的LSTM算法，它将LSTM中的忘记门和输入门替换为更新门，因此具有更简单的网络结构以及更少的训练时间. GRU的基本单元如图1所示，单元的中间计算如下：

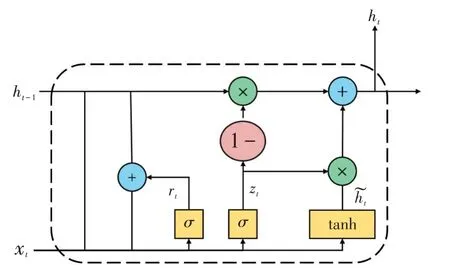
图1 GRU单元内部结构Fig.1 Internal structure of GRU unit

式中：zt和rt分别表示更新门和重置门，更新门决定了前一时刻的状态信息有多少被带入当前状态，更新门的取值越大表明带入的信息越多，重置门控制前一时刻的状态信息被带入候选集˜ht的程度，其取值越小，则被带入的信息越少；σ为sigmoid激活单元函数；f(·)为激活函数，通常选取为双曲正切函数tanh；*表示前后两个因素的点乘关系；Uz、Ur和Uh͂分别为权值矩阵；bz、br和bh͂为偏置值.

1.3 注意力机制

注意机制对深度学习任务有很大的改善作用，它是一种模拟人脑注意力的资源分配机制. 在某一时刻，人脑会将注意力集中在需要集中的区域，减少甚至忽略对其他区域的注意力，以获得更多的注意力. 注意机制通过概率分布将足够的注意力分配给关键信息，更多地注意到输入信号中更好地表达信号特性的那部分，提高模型的准确性. 大坝变形在复杂环境的影响之下，不同时间点的变形时间特征是不同的，当前测点可能受临近时间点变形信息的影响较大，二者所处环境因素更为接近. 同时随着时间间隔的增大，测点之间变形信息的影响也会逐渐减弱. GRU神经网络在分析变形时序关系时赋予不同时间点变形相同的权重，忽略了对当前变形影响较大时间点的变形特征，不能充分挖掘变形时序的非线性关系. 而Attention机制的引入，可以赋予不同时间位置的变形特征不同的注意力权重，使模型运行时聚焦于重要特征以提升模型的预测精度，且Attention 机制避免因变形时间序列过长导致的信息丢失问题，其结构如图2所示.

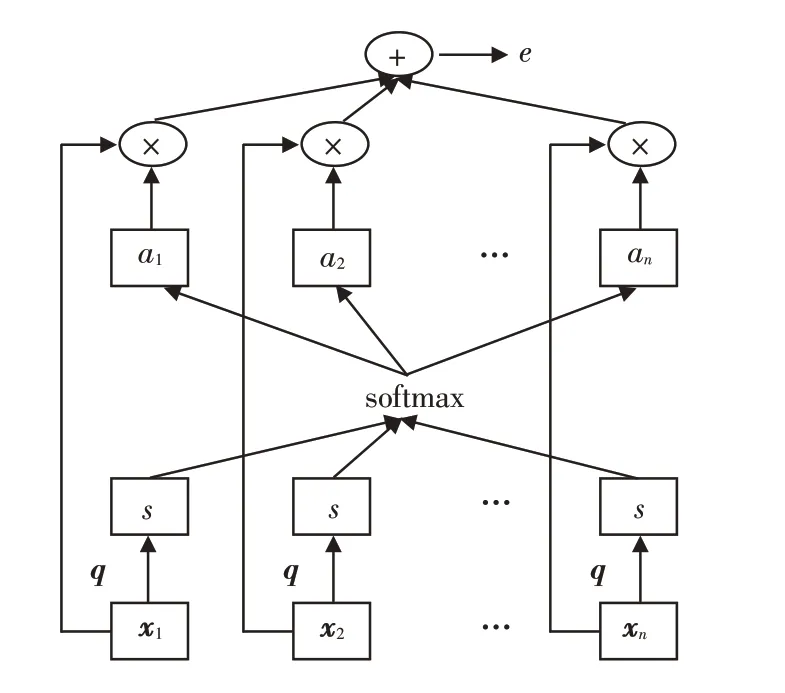
图2 注意力机制结构Fig.2 Structure of attentional mechanism

其中：V、W、U为学习参数；an表示注意力分布.

2 模型分析过程

2.1 EEMD-Attention-GRU模型预测流程

以第2节模型理论为依据，构建基于EEMD-Attention-GRU 模型的大坝变形组合预测模型，具体流程如图3所示，图中Dense表示全连接层.

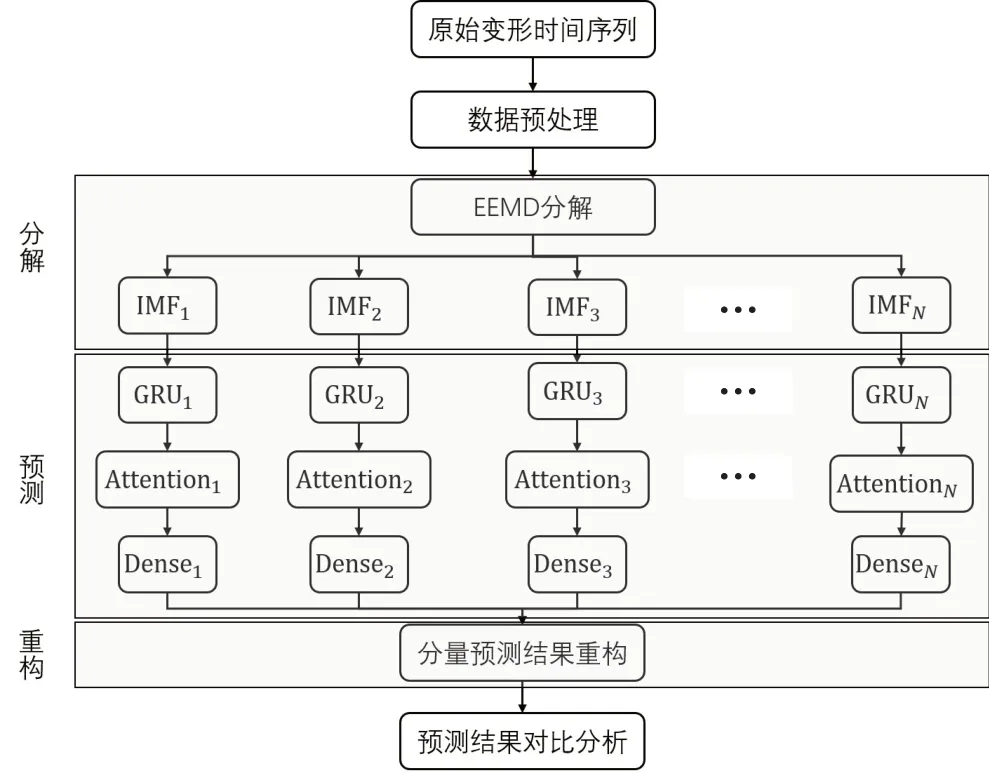
图3 EEMD-Attention-GRU模型流程图Fig.3 Flowchart of EEMD-Attention-GRU model

2.2 评价指标

本文选取平均绝对误差（MAE）和均方根误差（RMSE）等作为评价模型预测好坏的指标，具体公式见式（11）和式（12）：

式中：yi、pi分别表示变形原始值和预测值；n表示研究样本尺寸.

3 工程实例

3.1 数据获取和去噪

选取某混凝土连拱坝为研究对象，该坝上游水库总库容4.91 亿m3，正常蓄水位125.56 m，坝顶全长413.5 m，大坝坝顶高程为129.96 m，最大坝高75.9 m. 选取该坝水平径向位移作为本文建模依据，具体分析EEMD-Attention-GRU 模型在大坝变形预测中的可行性. 以大坝垂线系统位于13 坝段上的“PL13 上”测点2012年4月5日—2014年8月29日时段内共计877组径向位移数据为基础，按照2.1节的实施流程逐步分析，其中前827组数据划分为训练集、后50组数据划分为预测集，研究测点在相应时段内的变形信息如图4所示.

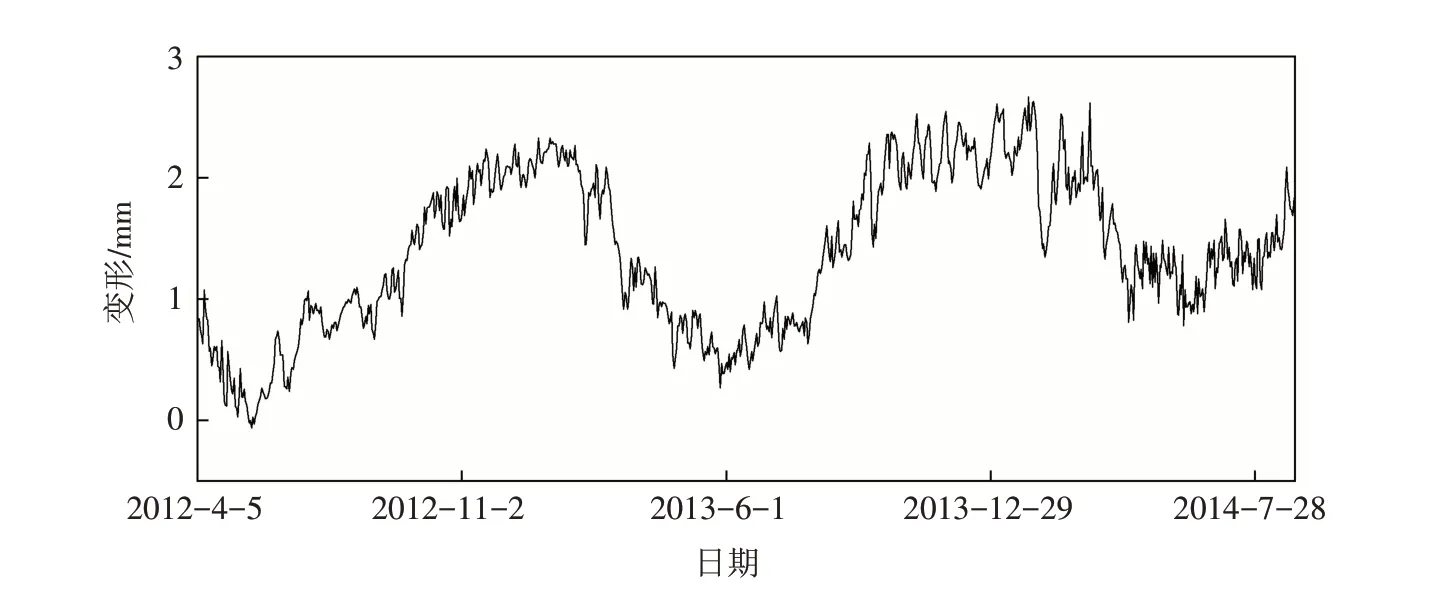
图4 研究测点变形信息Fig.4 Deformation information of the studied measurement points

通过图4可以发现，原始变形值包含大量噪声，噪声的存在将增加建模复杂度并导致模型的预测结果失真，进而影响对大坝行为性态的正确判断. 本文提出基于EMD的原始变形数据去噪方法，通过对原始数据的分解提取高频分量并保留剩余分量中包含的变形信息，去噪前后以及相应的噪声如图5所示. 由图可知，噪声部分杂乱无章，删除该部分无效分量将有效降低变形数据的非线性并简化建模过程，使预测结果更接近工程实际.

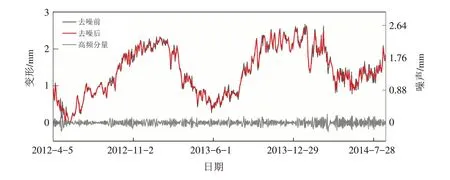
图5 噪声部分及去噪前后对比Fig.5 Noise part and comparison before and after denoising

3.2 EEMD分解结果

针对去噪后的变形数据，利用EEMD信号分解算法进行分解，得到如图6所示的IMF1-IMF9共计9个具有不同频率的变形分量. 同时可以看出，经过EEMD处理后的变形分量降低了变形数据的非线性和非稳态性，展现出一定的变形规律. 为了减小后续建模复杂度和计算消耗，将9个变形分量分成低频、中频和高频三种频率信号进行分别建模，其中低频包括IMF5-IMF9共计五个分量，中频包括IMF3和IMF4两个分量，高频包括IMF1和IMF2两个分量.

图6 EEMD分解结果Fig.6 Decomposition results of EEMD

3.3 算法实现和预测结果评价

上文中将基于EEMD 分解的九个变形分量分成了三组具有不同频率的变形分量IMF低频、IMF中频以及IMF高频. 本节分别对三种频率的变形分量构造Attention-GRU 预测模型，以前827组数据进行模型的训练，以剩余时段50组数据进行预测大坝的变形值.

为保证模型能够稳定输出高精度的预测结果，需对Attention-GRU神经网络的参数进行设置. 层数、训练批次batch_size、隐含层神经元个数、迭代次数epochs以及优化器等参数对模型预测精度的影响较大. 本文针对三种频率的变形分量统一构建单层GRU神经网络，且选择Adam作为梯度优化函数，以加快模型的收敛速度；计算过程中发现，batch_size的取值针对不同频率分量模型具有较强稳定性，因此将该值统一设置为65；IMF低频、IMF中频以及IMF高频对应的隐含层神经元数分别取值60、60和80，epochs的取值分别为200、250和250.

通过频率分组、数据集的划分以及参数的设置，对IMF低频、IMF中频以及IMF高频三种频率变形样本分别构建Attention-GRU预测模型，将模型的输出结果进行重组即可得到大坝变形的最终预测结果. 本文另外选取了EMD-GRU、GRU 两种方法作为对比分析，以验证EEMD-Attention-GRU 的有效性，各模型预测结果以及相应的残差如图7所示.

图7 不同模型对应的预测结果和残差Fig.7 Prediction results and residuals corresponding to different models

首先对比GRU和EEMD-GRU两个模型的变形预测结果，通过图7（a）可以看出，GRU模型虽然具有很强的时间非线性拟合能力，然而对于非线性、非静态的大坝变形数据来说，GRU模型相应的预测结果只能描述变形的大体走势，而不能准确反映其波动特征；当GRU模型与EEMD结合后分析得到的预测值更接近真实值，且波动程度明显接近真实值，说明EEMD算法在降低数据非平稳性、提升模型预测精度上有着不可或缺的作用. 对比分析EEMD-GRU 模型与EEMD-Attention-GRU 模型的预测能力，EEMD-Attention-GRU 模型的预测结果在变形“峰值”附近更接近真实值，说明Attention框架与GRU的结合能够提升算法对变形时序关系的挖掘能力以及对重要特征的筛选能力. 由图7（b）可以看出，文中提出的模型预测结果对应的残差曲线与y=0 所在位置包围的面积也是最小的，说明了提出模型的预测性能是优于其他模型的. 图8展现了不同模型在大坝变形预测中的性能评价指标条形图，研究的指标包括MAE、RMSE和R2. 该图直观反映了各模型变形预测结果的精度，GRU模型对应的三项指标均为三个模型中最差的，EMMD-GRU模型对应结果远优于GRU 模型但低于EEMD-Attention-GRU 模型. 再次验证本文提出的大坝变形预测方法的可行性，EEMD 和Attention 方法的引入分别从原始数据处理和深度学习网络框架内部机制两个方面优化GRU 模型，在延续GRU时序分析能力的同时拓展了其应用范围并提升了分析精度.

图8 模型预测结果评价指标Fig.8 Evaluation indicators of model prediction results

4 结论

本文提出了基于EEMD-Attention-GRU的大坝变形分析模型，该模型适用于非线性、非静态大坝变形的预测，预测精度显著高于其他方法. 主要结论总结如下：

1）从两个方面降低原始变形数据的非线性，即通过EMD高频分量的提取对原始数据进行去噪以及通过EEMD方法对变形数据进行分解，得到一组趋于稳定的变形分量.

2）构建Attention-GRU变形预测框架，提升模型对时序关系中关键特征的提取，并分别对三种频率的分量组合进行预测.

3）通过对预测结果的重构得到最终大坝变形预测结果，案例分析表明EEMD-Attention-GRU 的预测精度优于单一GRU模型和EEMD-GRU模型.