基于提升小波变换的矿区地表形变监测数据处理研究

2022-11-09杨俊山刘素洁杜春苗

河南科学 2022年9期

杨俊山，刘素洁，杜春苗

（1.河南省地球物理空间信息研究院，郑州 450000； 2.河南省地质物探工程技术研究中心，郑州 450000）

随着人口的增长，人们对矿产资源的需求急剧增加，而矿产资源开采常导致地质沉陷、滑坡等灾害，严重影响了矿区人民正常的生产生活. 因此，对矿区地表，特别是重点区域地表进行实时形变监测，研究其变化规律，对于及时发现地表形变及灾害预报预警具有重要意义.

在矿区地表形变监测及数据处理方面，研究人员开展了富有成效的工作. 栾元重和韩李涛［1］通过对矿区GPS变形监测网的建立、实时监测、基线平差、变形分析及分形特征等问题进行研究指出，地表点的移动具有较强的分形增长规律，GPS 变形监测技术能够揭示地表移动的非线性特征. 范洪冬［2］利用DInSAR、PS-DInSAR、SBAS等技术对天津市的失水沉降及某矿的开采沉陷监测进行了试验研究，阐述了SAR、InSAR、DInSAR 等技术的基本原理，分析了DInSAR 技术在沉降监测应用中的局限性. 然而，开采沉陷是一种大变形的地质灾害，仅仅采用DInSAR技术无法获得开采沉陷的主值以及完整的沉陷信息. 成晓倩等［3］为了弥补DInSAR提取大形变的不足，以DInSAR和PIM结果组成的混合数据为数据源，采用Gauss模型重建开采沉陷主断面，实现了下沉特征曲线数学模型的重建. 王伟等［4］利用卫星导航定位基准站（CORS）网全球卫星导航系统（GNSS）对区域地面大地高、地面重力和地倾斜变化进行了连续监测，同时通过与部分地质灾害信息进行时空分析，确定了用于地面稳定性变化分析的要素和权重，进而定量分析了地面稳定性变化. 虽然GPS技术的精度较高［5］，但是其观测点的空间密度低、观测周期长，并且GPS 测站及观测点布设与维护较为困难，布设的观测点极易遭到破坏. DInSAR 技术主要用于短时期的形变研究，而在进行长时间、缓慢地表形变监测时，会受到时/空基线失相干以及大气效应等因素的影响，存在精度低、结果可靠性较差的问题［6-7］，同时DInSAR 技术常需要有针对性地购买区域高精度影像数据，监测成本较高. GNSS是利用接收上空的卫星信号实现定位的，静态测量精度能达到厘米级甚至毫米级，在复杂山区具有独特的优势. GNSS形变监测具有测站间无须通视和全天候自动观测等优点，但由于GNSS数据采集过程中易受天气、树木遮挡、多路径效应等多种因素影响，因此GNSS形变序列中常包含测量噪声，这些噪声会严重影响有效形变信息的提取和测量精度，导致监测物的形变信息不准确［8-9］. 因此，如何从严重干扰的信号序列中提取出有效的形变信息、提高GNSS形变监测解算的精度和稳定性至关重要.

傅里叶变换能够把信号映射到频域内，提取信号的频谱，然后利用信号的频谱特性分析时域内难以看清的问题，但其无法反映某一局部时间内信号的频谱特性，因此可能会忽略短时间内的信号变化［10-13］. 小波变换继承并发展了短时傅里叶变换局部化的思想，能够克服窗口大小不随频率变化的缺点，是进行信号时频分析处理的理想工具，当前已应用于信号去噪及信息提取等方面［14-16］. 小波变换能够充分突出问题某些方面的特征，实现对时空频率的局部化分析，并通过伸缩和平移运算对信号进行多尺度分解与细化，获取信号的细节. 小波去噪其实就是抑制信号中的无用部分、恢复信号中的有用部分的过程［17-18］. 在小波变换的基础上，提升小波变换能够通过提升模式构造出小波函数，减小常规小波变换计算的复杂度，提高运算速度［19-21］，因而被广泛应用于大地测量中.

为了削弱GNSS监测数据中的干扰噪声、提取有效的监测形变信息、提高数据解算精度，本研究以河南某矿区的GNSS监测数据为研究对象，将提升小波变换方法引入到GNSS监测数据处理中，对该矿区多个监测点的GNSS监测数据进行了提升小波降噪及分解解算处理，并对比分析了常规Kalman滤波动态解算方法和提升小波降噪解算方法对GNSS监测数据解算的精度和稳定性.

1 提升小波变换及Kalman滤波动态解算的基本原理

1.1 提升小波变换的基本原理

提升小波变换算法是对传统小波变换的一种改进，小波函数也不再由函数的平移和伸缩而产生，所有的运算都在时域上进行，能够在一定程度上减少计算量，提高监测数据的解算效率. 提升小波变换应用于信号去噪时，首先是对分解后得到的低频近似信号和高频细节信号进行一些处理，然后再进行完全的反向重构，即提升小波变换包含了分解和重构两个过程.

1.1.1 分解过程

提升小波变换的分解过程包括3个步骤，即分裂、预测、更新［20］. 具体过程如下：

1）分裂. 将获取的监测信号序列Sn分解成奇信号序列S2n+1和偶信号序列S2n，n=1，2，3，…. 除按奇偶信号序列划分外，还可按其他方法进行分裂.

2）预测. 在分裂完成之后即可进行预测. 预测是在初始监测信号序列相关性的基础上，通过预测算子P利用偶信号序列预测奇信号序列，用预测奇信号序列值与实际奇信号序列值之差（即预测误差δn）代替奇信号序列，以此来表示信号序列细节信息.

预测误差δn可视为原信号序列的高频部分.

3）更新. 更新过程利用更新算子U来处理预测误差δn，然后将处理结果叠加至偶信号序列以对其进行更新，得到近似信号（又称尺度系数T）.

通过重复上述3个步骤即可实现多尺度、多分辨率的提升小波变换.

1.1.2 重构过程

提升小波变换重构过程包含反更新、反预测及合并3个步骤，过程如下：

1）反更新. 给定信号Tn和预测误差δn，则可恢复偶信号序列.

2）反预测. 获取偶信号序列之后，即可通过预测数据恢复奇信号序列.

3）合并. 利用加法运算即可得到原信号序列.

在提升小波变换中，预测与更新是算法的核心，利用预测过程能够获取监测信号中的高频信息，而利用更新过程则可获取监测信号中的低频信息. 因此，在变换时首先可将原始监测信号分解为尺度系数及新的小波系数，根据有效形变信息及噪声信息对应的系数确定合适的阈值，然后利用提升小波算法对系数进行反变换，即可完成对监测信号的降噪. 降噪之后，对监测信号进行小波多尺度分解，得到分解后的信号在各个频段的分布状况，根据前期统计分析结果，可提高分解后的处理效率，削弱干扰噪声的影响，提取有效的监测信息.

1.2 Kalman滤波动态解算的基本原理

在GNSS监测数据处理中，常采用Kalman 滤波算法进行动态解算. 在Kalman 滤波中，如果系统状态噪声和观测噪声均符合Gaussian分布，则离散线性状态模型如公式（6）所示.

式中：Xk表示状态向量；Φk/k-1表示状态转移矩阵；Zk表示观测向量；Hk为观测矩阵；Wk和Vk分别表示状态噪声和测量噪声. Kalman滤波方差准则如式（7）所示.

式中：vk和vk/k-1分别表示观测向量的残差和预测状态向量的残差；Pk/k-1表示预测状态向量的协方差矩阵；Rk表示观测噪声的协方差矩阵；min表示最小.

在Kalman滤波方差准则下可得到Kalman滤波解，即：

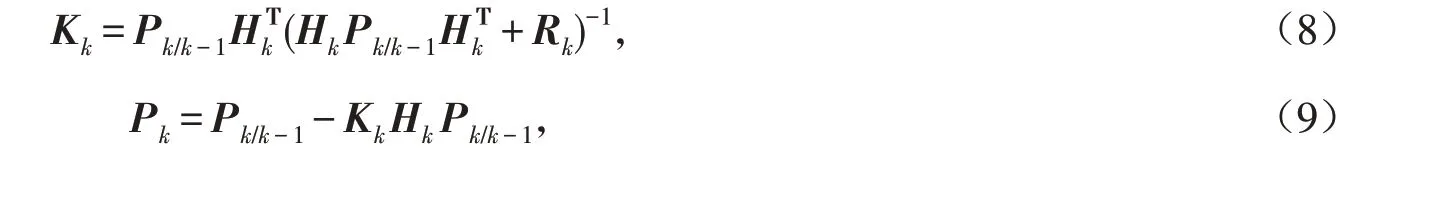
式中：Xk/k-1和Pk/k-1分别表示预测状态向量及其协方差矩阵；Rk表示观测噪声的协方差矩阵；Kk表示增益矩阵；Xk表示状态向量；Hk为观测矩阵；Pk为Xk的协方差矩阵；Zk为观测向量.

2 GNSS监测数据的处理分析

河南某矿区位于河南西部地区，东起沙河与汝河交汇带的洛岗断层，西抵红石山附近的郏县断层，南至湛河北岸的煤层露头，北达汝河附近的襄郏断层，东西长约40 km，南北宽约20 km，含煤面积约650 km2. 受地势及环境影响，该矿区地形复杂，难以采用传统水准测量方法对其地表进行形变监测. 另外，由于DInSAR技术存在成本较高的问题，难以适用大范围区域长期的地表形变监测工作，因此近年来一直是在该矿区建设的CORS站的基础上利用GNSS技术对其进行地表形变监测. 但在长期的监测工作中发现，监测解算出的形变量与实际形变量常存在不符合的情况，有的监测点监测解算出的形变量与实际形变量的差距还相对较大，无法忽略不计. 通过分析得知，这是因为得到的GNSS监测数据受噪声干扰较为严重，易淹没有效形变信息. 因此本研究以该矿区多个监测点的GNSS监测数据为研究对象，先采用提升小波变换方法对该矿区的GNSS监测数据进行降噪处理后再对其进行解算，以期获取更为精确的地表形变信息. 同时，为了验证提升小波变换在GNSS形变监测数据处理中的有效性，分别对该矿区的GNSS监测数据进行了常规Kalman滤波动态解算（算法一）和提升小波降噪解算（算法二）. 以监测点BD25为例，图1给出了通过不同算法解算得到的该点的位置误差.

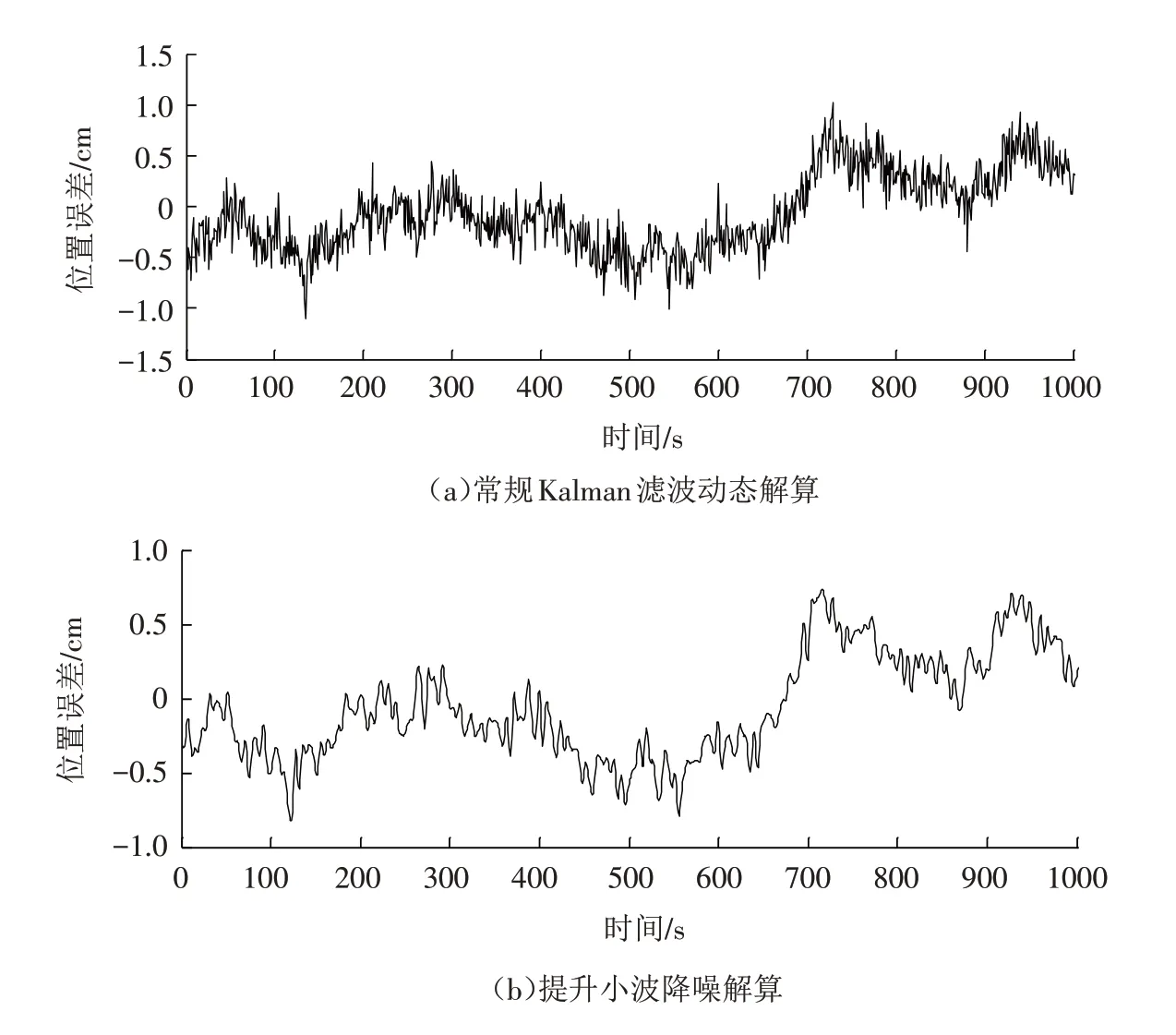
图1 通过不同算法解算得到的BD25监测点的位置误差Fig.1 Position errors of the monitoring point BD25 obtained by different algorithms

由图1可知，通过提升小波降噪解算方法得到的位置误差整体比通过常规Kalman滤波动态解算方法得到的位置误差小，这说明经过提升小波变换处理之后，干扰噪声被明显削弱，GNSS 监测信号得到了明显改善，所以最终的定位解算精度明显得到提升. 从图1还可以看出：通过常规Kalman 滤波动态解算方法得到的位置误差在1.5 cm以内，绝大部分历元的位置误差在1.0 cm以内；通过提升小波降噪解算方法得到的位置误差在1.0 cm以内，精度相对较高. 因此，在实际的矿区地表形变监测中，建议使用提升小波降噪解算方法对GNSS监测数据进行解算，因为通过该方法能够有效削弱干扰噪声的影响，获取有效的监测位移信息，且监测精度能够满足基本需求.

由于矿区的环境复杂，因此很多情况下，监测信号受到的干扰是未知的，无法有效判断干扰源，而通过分析监测点的位置误差振幅和频率可在一定程度上为未知干扰的判断提供依据. 以BD25监测点为例，通过绘制该监测点提升小波降噪解算方法的频谱图，得到了该监测点的位置误差振幅和频率，如图2所示. 从图2可以看出，大部分历元解算的位置误差在5 mm 以内，而这些信号的频率多集中在0～0.5 Hz 之间，这为后续有效形变监测位移信息的获取提供了帮助.

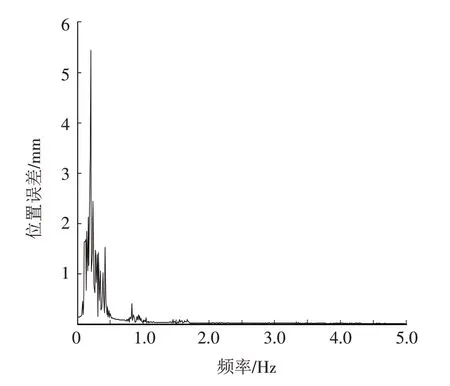
图2 BD25监测点提升小波降噪解算方法的频谱图Fig.2 Spectrum diagram of lifting wavelet denoising method for the monitoring point BD25

为进一步对比分析不同算法的性能，随机选取该矿区6 个监测点（AD6、AD8、AD25、BD25、BD28、CJ15）的监测数据为研究对象，分别用两种算法对这6个监测点的GNSS监测数据进行解算，得到各监测点的位置误差如表1所示.

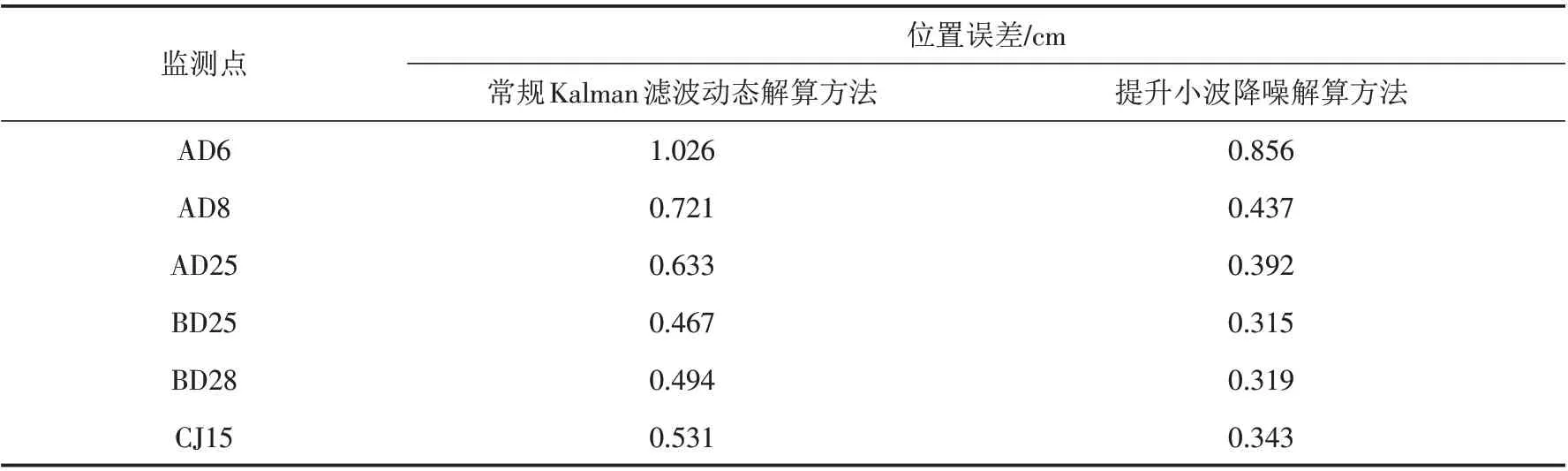
表1 通过不同算法解算得到的各个监测点的位置误差Tab.1 Position errors of each monitoring point calculated by different algorithms

从表1可以看出，通过提升小波降噪解算方法解算获取的位置误差明显小于通过常规Kalman滤波动态解算方法解算获取的位置误差，这是由于提升小波变换解算方法能够有效削弱干扰噪声的影响. 通过设定合理的阈值，能够排除相关频段的噪声信号，从而有助于获取有效的监测信息，这不仅能够为复杂环境下矿区地表GNSS静态形变监测技术提供帮助，还能为动态定位解算及其他领域的提升小波变换应用提供借鉴.从表1还可以看出：通过常规Kalman 滤波动态解算方法解算出的各监测点的位置误差相差较大，这与各个监测点的位置及周边监测环境有关；通过提升小波降噪解算方法解算出的各监测点的位置误差整体相差较小，但仍存在个别位置误差较大的点，这可能是因为在预处理解算中并未完全剔除观测粗差，导致解算结果出现较大偏差. 因此，在前期预处理解算过程中，可根据实际解算效果合理调整粗差探测的阈值，有效削弱观测粗差的影响，以便在后续处理中进一步提高解算的精度.