轻质橡胶颗粒-砂混合土的压缩性试验研究

顾尧天， 刘家兴

（1.河海大学岩土力学与堤坝工程教育部重点实验室，南京 210024；2.苏州工业园区公共资源交易中心，江苏苏州 215127）

随着经济的迅速发展，汽车的数量不断增加，这将导致废弃橡胶轮胎的数量越来越多. 目前，我国通常采取焚烧、填埋和堆积的方式处理废弃橡胶轮胎［1］. 然而，焚烧会产生大量的有毒气体，污染空气、土地；填埋不当会对土体和地下水造成很严重的污染，严重破坏生态环境；堆积会滋生大量有害寄生虫，这些处理方式都会造成环境的污染和资源的浪费. 因此，资源化利用废弃轮胎橡胶显得尤为重要.

相较土体而言，橡胶自身具有质量轻［2］、耐久性好［3］、渗透性低［4］、变形能力强［5］、阻尼比高［6］等特点. 因此，多个国家和地区将废弃橡胶轮胎加工成碎片或者颗粒应用到工程当中. 轻质橡胶颗粒混合土具有质量轻、渗透性好［7］、侧向变形小［8］、抗震能力强等优点. 通常可将轻质橡胶颗粒混合土应用于软基换填、公路路基［9］、边坡、挡土墙［10］等工程，也可应用于结构物的动载缓冲［11］和抗震［12］中. 辛凌等［13］在混合土中掺入水泥作为固化剂以提高混合土的强度，增大抗变形能力. 目前，国内对轻质橡胶颗粒混合土的研究及工程应用案例较少，现有研究大多针对经水泥等材料固化后的橡胶颗粒混合土开展试验，由于耦合作用各因素相互干扰，难以区分单一因素的影响，特别是没有考虑橡胶颗粒本身的压缩对混合土基本力学特性的影响. 因此需要对该混合土进行更加深入的研究，以更好地掌握轻质橡胶颗粒混合土的基本力学特性.

本文的研究对象仅限于橡胶颗粒和砂颗粒组成的混合土，从而避开固化剂和水的干扰，以探究橡胶颗粒的压缩性对混合土力学性质的影响. 通过一系列的单向压缩试验，研究了纯橡胶颗粒试验和轻质橡胶颗粒-砂混合土的压缩性，并建立单向压缩试验条件下混合土压缩模型，分析橡胶颗粒的掺量对轻质橡胶颗粒混合土基本力学性质的影响规律.

1 单向压缩试验

1.1 试验材料

试验材料采用橡胶颗粒和砂颗粒. 橡胶颗粒由废旧轮胎橡胶经机械破碎后得到，比重为1.17，平均粒径为0.53 mm；砂颗粒为福建标准砂，比重为2.62，平均粒径为0.61 mm，级配曲线如图1 所示. 试验所用的橡胶颗粒和砂土均为干燥颗粒，且不掺固化剂.

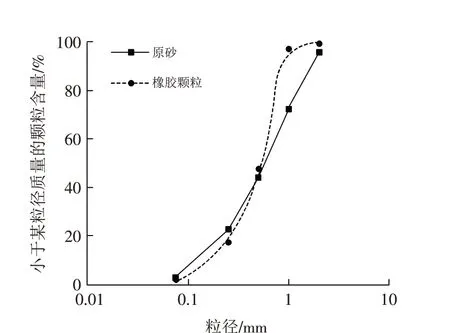
图1 砂颗粒和橡胶颗粒粒径分布曲线Fig.1 Particle size distribution curves of sand particles and rubber particles

1.2 试验方案

单向压缩试验采用的仪器为WG型单杠杆固结仪.试样的高度为20 mm，直径为61.8 mm. 通过对不同橡胶质量分数Mr的混合土进行单向压缩试验，得到混合土竖向应变与竖向压力之间的关系，从而分析得出混合土的压缩性随橡胶掺量之间的变化关系，试验方案如表1 所示.由式（1）计算得到各质量分数Mr所对应的体积分数Vr也列在表1中. 为研究橡胶颗粒自身压缩性，还另外开展一组对照试验，该样本中原料土为砂土，调整其粒径分布曲线与橡胶颗粒一致.

表1 单向压缩试验方案Tab.1 Scheme of uniaxial compression test

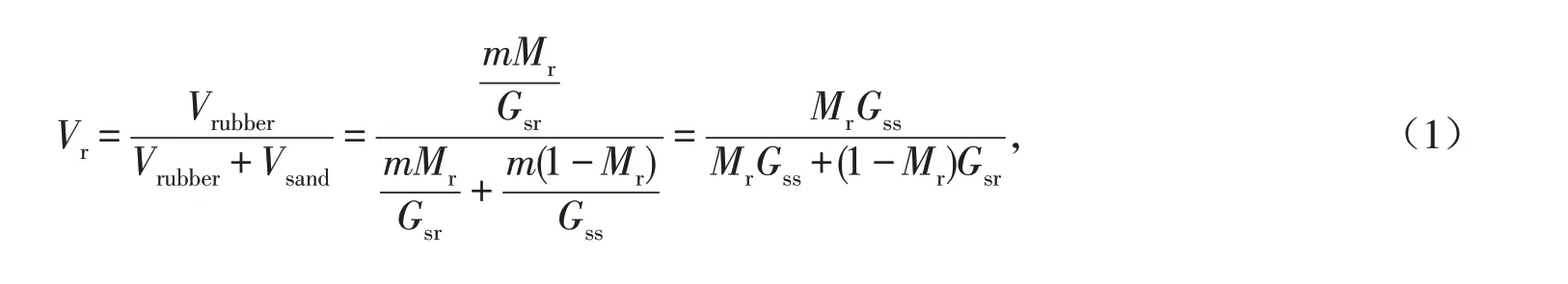
其中：Vrubber为混合土中橡胶颗粒的体积；Vsand为混合土中砂颗粒的体积；m、Gss和Gsr分别代表混合土的总质量、砂粒比重和橡胶颗粒比重.

1.3 试样制备及试验过程

试验所用的材料为自然风干的橡胶颗粒和烘干的砂颗粒，按照橡胶质量分数Mr称取材料，采用干拌混合法将橡胶颗粒和砂颗粒混合均匀，形成轻质橡胶颗粒-砂混合土. 为保证试样的可比性，制样时控制试样的相对密实度为0.7. 为避免振动击实对试样中颗粒的均匀性造成影响，在制样时，以按压的方式将轻质橡胶颗粒混合土分为五层依次装入固结仪中，单向压缩试验试样制备过程如图2所示.

图2 单向压缩试验过程Fig.2 Process of uniaxial compression test

将固结容器放置在固结仪台座上，在固结容器中依次放入底部透水石、护环、滤纸、环刀，在放置好的固结容器中装入混合均匀的轻质橡胶颗粒混合土，制样方法如上述. 装样完成后，在试样上方放置滤纸、透水石、加压板和钢珠. 在上述步骤完成后，将试样置于加压框架正下方，使加压头对准钢珠，安装百分表，记录初始读数. 试验开始前对试样施加1 kPa预压荷载，记录百分表读数，调整百分表使指针读数为0，试验开始. 施加荷载的原则为试样在上级荷载压力作用下变形稳定后（1 h变形不超过0.005 mm），施加下一级荷载.

2 轻质橡胶颗粒-砂混合土的压缩性模型

2.1 压缩机理分析

在竖向压力作用下，轻质橡胶颗粒-砂混合土的压缩量包括了橡胶颗粒自身的压缩变形量与孔隙的减小量，混合土的变形机制如图3所示. 当混合土中橡胶颗粒掺量较多时，橡胶颗粒与砂颗粒之间随机分布，橡胶颗粒被压缩填补砂颗粒-砂颗粒之间的空隙，混合土的压缩主要由橡胶颗粒自身的压缩以及橡胶颗粒与砂颗粒之间的重新排列引起的骨架变形所致；当橡胶掺量较少时，在竖向压力作用下橡胶颗粒被压缩，砂粒均匀分布在橡胶颗粒周围，压力继续增大时，颗粒会产生相应的滑移滚动，致使混合土密实，此时混合土的压缩主要由颗粒间的颗粒重新排列所致.

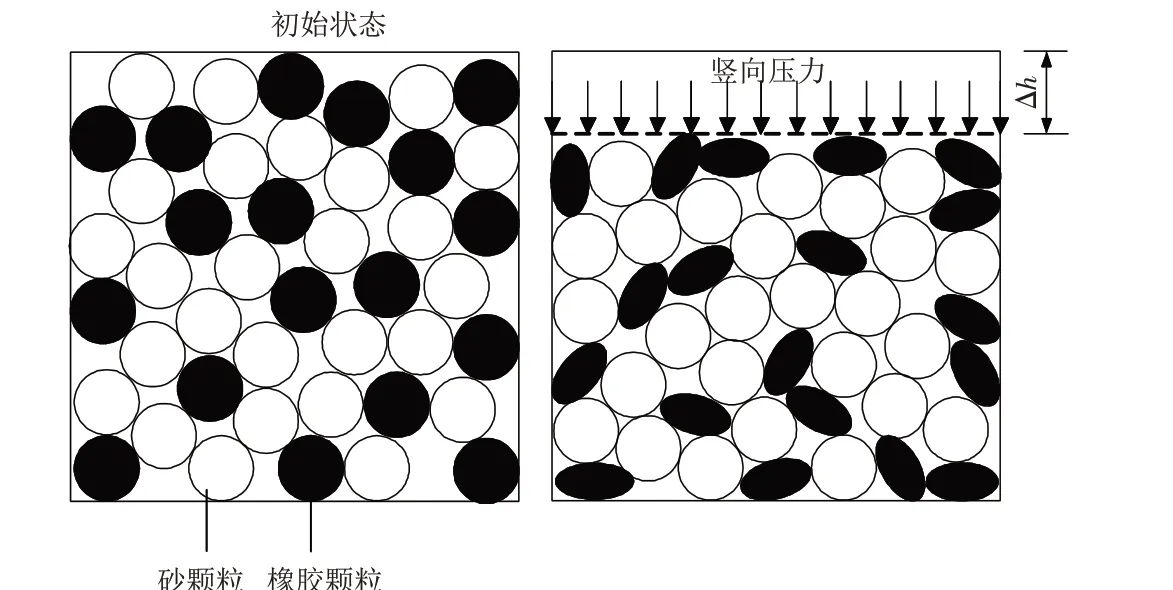
图3 轻质橡胶颗粒-砂混合土变形机制示意图Fig.3 Schematic diagram of deformation mechanism of lightweight granulated rubber-sand mixtures

2.2 压缩模型的提出

已有学者提出了无黏性土的压缩模型［14-17］，一般是在试验的基础上总结得到的，没有明显的收敛极限，实用性较强. 由于本文采用的混合土为橡胶颗粒和砂颗粒组成，均为无黏性颗粒，因此参照无黏性土压缩模型进行研究. 在压缩性研究中，一般认为土体颗粒不可压缩，土样的压缩主要由孔隙减小所致. 而邓安等［18］指出，在压力作用下，轻质橡胶颗粒的体积变形不可忽略. 根据本文的试验结果也发现，橡胶颗粒的压缩性较强，且纯橡胶试样中橡胶颗粒自身的压缩变形量比孔隙的减小量大得多，因此轻质橡胶颗粒-砂混合土的压缩量等于橡胶颗粒自身的压缩量和与混合土颗粒级配相同的纯砂试样的孔隙减小量之和. 本文在研究轻质橡胶颗粒-砂混合土的压缩性时，考虑轻质橡胶颗粒自身的压缩性对混合土压缩性的影响.

在理论分析之前，做了如下假设：①砂颗粒为刚性颗粒，在压力作用下不发生变形；②轻质橡胶颗粒-砂混合土中两种颗粒均匀分布；③单向压缩试样无侧向变形；④橡胶颗粒可压缩，混合土的单轴压缩量等于橡胶颗粒的压缩变形量与孔隙的减小量之和，后者等于与混合土颗粒级配相同的砂土的孔隙减小量.

3 试验结果与分析

3.1 橡胶颗粒压缩模型

土力学中，体积压缩系数mv为土体在单位压力作用下单位体积的变化，即mv=dεv/dp，εv为竖向压力下的体变，p为竖向压力，压缩模量与体积压缩系数之间的关系为Es=1/mv=dp/dεv. 根据假设③可知，在单向压缩条件下，橡胶颗粒试样的体变实际上等于竖向应变，即ε=εv，ε为竖向应变. 通过试验分别获得纯橡胶颗粒试样和与橡胶颗粒级配相同的纯砂试样在不同荷载下的压缩量，两者之差则为橡胶颗粒自身的压缩量. 单轴压缩条件下，橡胶颗粒自身压缩性试验结果如图4所示，当竖向压力增加时，橡胶颗粒的竖向应变呈指数增加，应变增量逐渐减小，体积压缩系数逐渐减小，压缩模量逐渐增大.

图4 橡胶颗粒自身压缩模型公式拟合结果Fig.4 Fitting result of compression model formula for rubber particle

橡胶颗粒的压缩模量随竖向压力的增加而增大，在此过程中，橡胶颗粒的竖向应变逐渐增加. 一般来说，竖向总应变越大，橡胶颗粒在单位压力下对应的压缩量越小，压缩模量逐渐增加. 因此，可认为橡胶颗粒Es不仅与竖向压力p呈正相关关系，还与当前的竖向应变ε呈正相关关系. 为定量描述压缩模量，现做出如下假设：

1）压缩模量Es与当前的竖向应变有关的函数f1和竖向压力p有关的函数f2的乘积成正比，即：

式中：α为比例系数.

2）函数f1可以表示为：

对于f2，根据Lee等［19-20］的研究可知，橡胶颗粒的压缩模量与竖向压力的关系可近似用指数函数表示：

式中：β为橡胶颗粒材料参数，对于颗粒比重相同、级配相同的橡胶颗粒，β为常数；pa为标准大气压.

结合公式（3）和（4），公式（2）可以表示为：

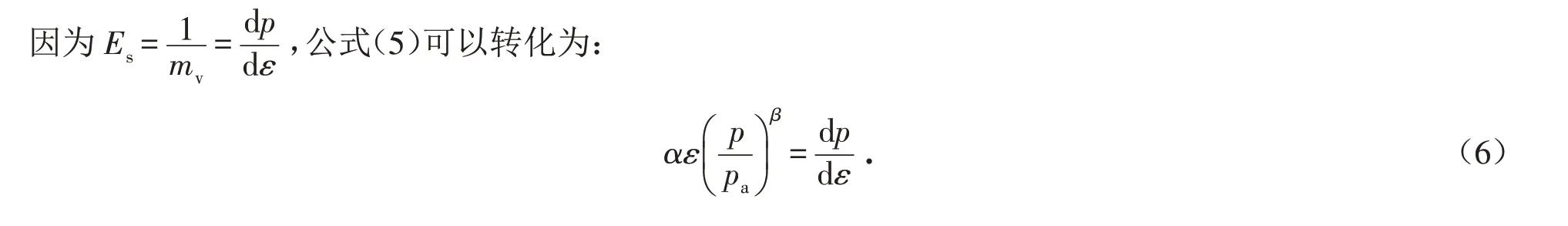
对公式（6）积分可得，在任意竖向压力p下，橡胶颗粒自身的竖向应变为：

式中：参数α可以利用试验数据根据式（7）优化拟合来确定.

注意到，β表示橡胶颗粒自身的竖向应变ε随竖向压力p的变化率，由于橡胶颗粒自身的压缩模量随竖向压力的增加而增大，因此β＞0，且β的取值直接影响式（7）所对应曲线的形式，根据图4中试验数据可以推断（1-β）/2＞0，因此β的取值介于0～1之间. 橡胶颗粒压缩模型公式拟合结果与试验数据之间的对比曲线如图4所示，根据试验数据拟合确定公式（7）中α、β分别为2 211.656 0、0.184 5. 其中α取值较大的原因是在分析时，压缩模量Es的单位为MPa，竖向压力p的单位为kPa.

3.2 原砂试样压缩模型

由于研究对象为标准砂且竖向压力小于400 kPa，属于低应力状态，可以参照赵颜辉等［21］提出的压缩模型，原砂试样的竖向应变表示为：

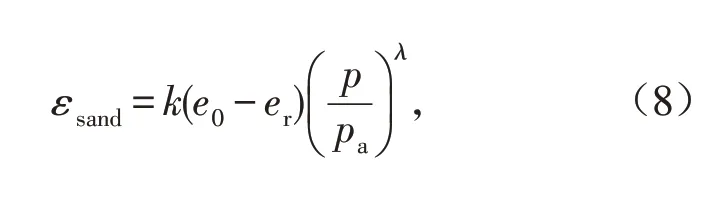
式中：k、λ为参数；e0、er分别为砂试样的初始孔隙比和参考孔隙比.

原砂试样压缩模型公式拟合结果与试验数据之间的对比如图5 所示，已知初始孔隙比e0=0.503 1，根据试验数据确定公式中k、er、λ分别为0.000 89、0.327 和0.716 7. 试验数据与公式拟合曲线之间差距较小，拟合程度较好.

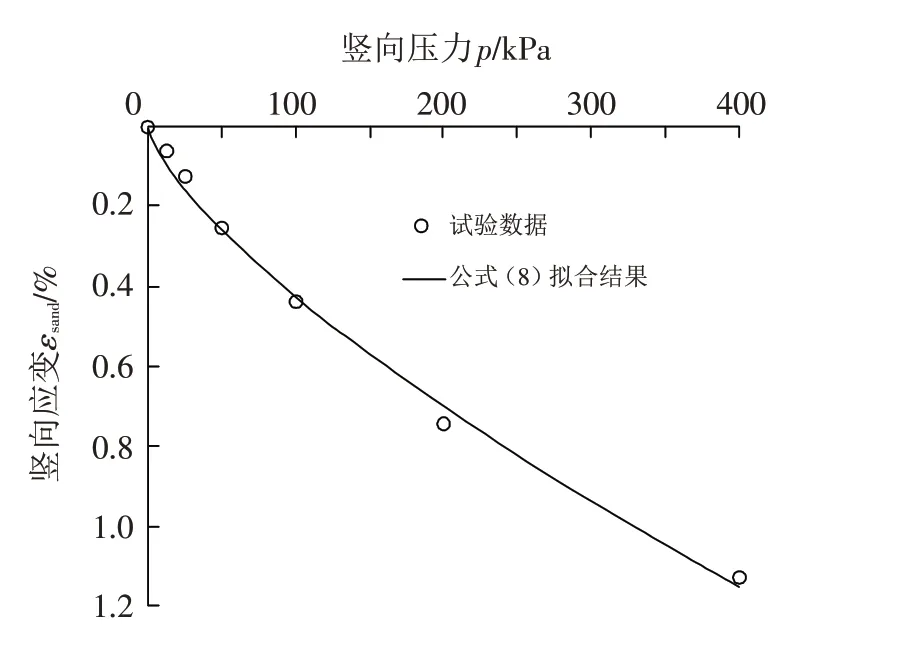
图5 原砂试样压缩模型公式拟合结果Fig.5 Fitting result of compression model formula for sand sample

3.3 轻质橡胶颗粒-砂混合土压缩模型

由于混合土为无黏性土，可参考无黏性土的压缩模型进行推导. 基于假设（4），混合土的压缩模型公式可以表达为：

式中：εco为橡胶颗粒-砂混合土的竖向应变；κ、η为折减系数. 将公式（7）和（8）代入，可得：

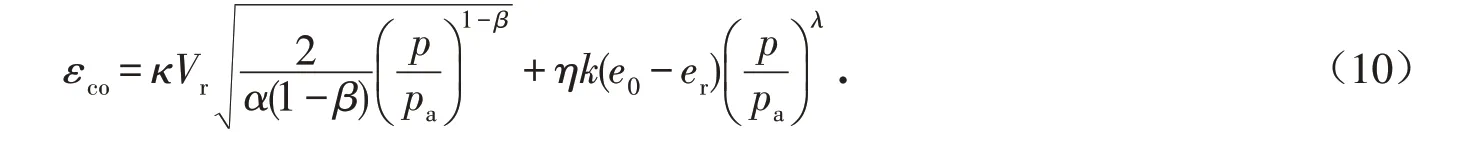
首先解释κ和η的含义，κ为橡胶颗粒在混合土中的变形限制系数，取值应介于0～1之间. 在橡胶颗粒压缩模型中，由于橡胶颗粒为柔性颗粒，在压力的作用下橡胶颗粒发生体积变形，此时周围的橡胶颗粒也会随之变形，颗粒之间变形连续；而在橡胶颗粒-砂混合土的变形中，橡胶颗粒周围不再只有柔性颗粒，而有可能是砂颗粒. 假设①认为砂颗粒为刚性颗粒，因此在压力作用下，砂颗粒不会随橡胶颗粒发生变形，此时砂颗粒的存在对橡胶颗粒起到抑制作用，因此折减系数κ＜1.η表示在单向压缩试验条件下，与原砂试样相比混合土的颗粒重排能力. 当Vr＞0时，在压力的作用下，橡胶颗粒产生压缩变形，被压缩的橡胶颗粒填补砂颗粒之间的孔隙，此时混合土中颗粒重排的能力比纯砂强，因此折减系数η≥1.

橡胶颗粒-砂混合土压缩模型公式拟合结果与试验数据如图6所示，从图中可见公式拟合程度较好. 不同橡胶体积分数下折减系数κ和η与橡胶体积分数Vr关系曲线如图7所示. 折减系数-橡胶体积分数拟合公式见表2.

表2 折减系数-橡胶体积分数拟合公式Tab.2 Fitting formulas of reduction coefficients and volume fractions of rubber

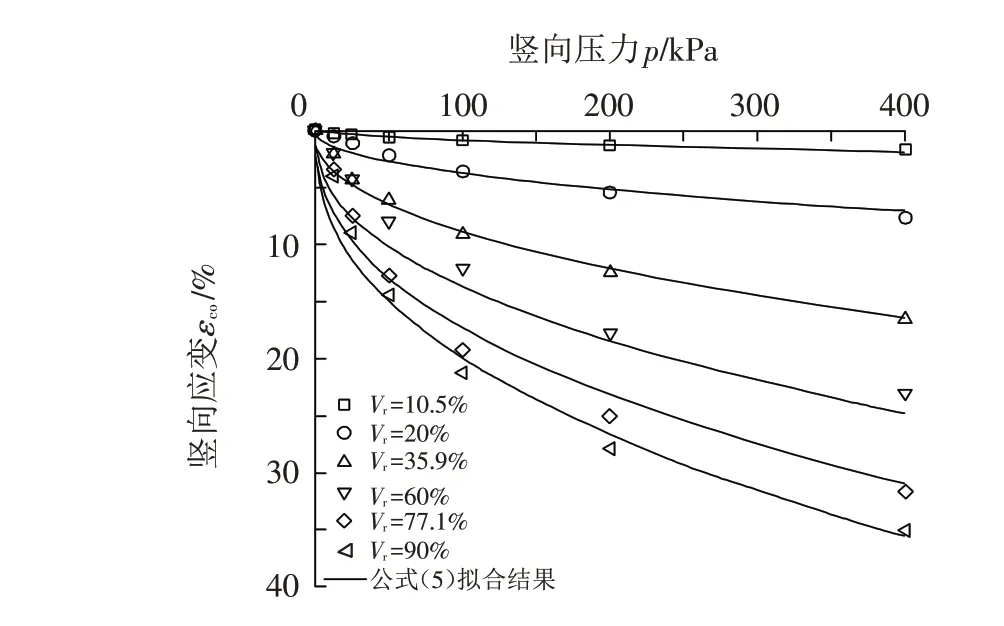
图6 轻质橡胶颗粒-砂混合土压缩模型公式拟合结果Fig.6 Fitting results of compression model formula for the lightweight granulated rubber-sand mixtures

图7 折减系数随橡胶体积分数变化曲线Fig.7 Variation curves between reduction coefficients and volume fractions of rubber

如图7所示，混合土压缩公式中的折减系数κ随橡胶掺量（Vr）的增加而增大；η随Vr的增加先增大后减小，分界点为Vr=35.9%. 根据图7中κ随Vr的变化规律来看，当橡胶体积分数小于35.9%时，混合土中的主要由砂颗粒承担压力，抵抗变形能力较强，在压力作用下混合土的变形较小，压缩模量较大；当橡胶体积分数大于等于35.9%，混合土中抵抗压缩的能力主要由橡胶颗粒承担，压缩性较高，压缩模量较小且与纯橡胶颗粒试样接近. 当橡胶体积分数Vr=35.9%，η=2.449，该点也作为图7中η-Vr曲线的分界点，可以推测在该橡胶掺量情况下，混合土颗粒重排能力最强. 当橡胶体积分数Vr＜35.9%，η增加的原因在于橡胶颗粒的增多使得压力作用下的混合土的颗粒重排能力增强；当Vr＞35.9%，η随橡胶体积分数的增加而减小，原因是在计算单向压缩试验中橡胶颗粒自身的压缩性时，假设橡胶颗粒试样的压缩性等于橡胶颗粒自身的压缩性和与橡胶颗粒级配相同的砂的颗粒重排引起的压缩之和，而实际上橡胶颗粒的颗粒重排能力要比砂颗粒好，因此在计算橡胶颗粒自身压缩性时数值偏大. 当混合土中橡胶颗粒掺量较多时，这将使得混合土橡胶颗粒自身的压缩量的计算值比实际值大，因此导致η随橡胶体积分数的增加而减小. 当Vr=90%时，η接近于1，而此时κ=1，这也证明了计算混合土压缩量公式的合理性.

4 结论

本文通过单向压缩试验研究了轻质橡胶颗粒-砂混合土的压缩性，主要得到如下结论：

1）相同竖向压力条件下，随着橡胶掺量的增加，轻质橡胶颗粒-砂混合土的竖向应变逐渐增大，压缩模量随之减小，抵抗变形的能力减弱.

2）本文得到的纯橡胶颗粒试样压缩模型，能很好地反映单向压缩条件下橡胶颗粒自身的变形特性；考虑混合土的压缩量等于橡胶颗粒自身压缩量与孔隙减小量之和，结合原砂试样压缩模型得到的橡胶颗粒-砂混合土的压缩模型，能较好反映混合土的压缩变形性状.

3）橡胶体积分数Vr=35.9%（对应的橡胶质量分数Mr=20%）为混合土压缩性的界限橡胶掺量，当橡胶颗粒掺量超过界限橡胶掺量时，混合土中的压力从主要由砂颗粒承担逐渐变为主要由橡胶颗粒承担，混合土的压缩性较高. 因此，建议在工程应用中选择橡胶质量分数小于20%的混合土作为轻质填料.