基于混合策略的电子鼻在线漂移抑制算法

陶 洋，李 强，吴 鹏

(重庆邮电大学通信与信息工程学院，重庆 400065)

0 引言

1994年，由Gardner发表的文章中对电子鼻系统做了完整的解释：电子鼻系统是一个由不同专一性传感器构成的传感器阵列，同时再辅以信号处理及模式识别算法，最后用于单一或者复杂的气体检测[1]。

近年来，随着材料技术的更新以及模式识别算法的迅速发展，电子鼻系统在各领域均得到了广泛的应用。例如Z. B. Wei等开发了一套由12个金属氧化物传感器集成的便携式电子鼻系统，并将其应用于不同年份的米酒识别[2]。M. Rivai等用3种气体传感器和1个颜色分类传感器阵列研发了电子鼻系统，用于对肉类的新鲜、半腐烂、腐烂状态进行分类识别，并取得了较高的实验精度[3]。C. Sanchez等用研发的电子鼻系统结合主成分分析和人工神经网络来对酒精含量不同的啤酒进行识别[4]。T. M. A. Sabeel等将Cyranose E-320电子鼻系统用于早期糖尿病和细菌感染检测中[5]。

电子鼻在环境监测、食品安全、医疗辅助等行业应用广泛。传感器自身的漂移问题是电子鼻最突出的问题之一。传感器漂移即传感器在长期使用的过程中，因为自身硬件老化及环境变化导致的传感器的输出响应偏离正常值的情况。针对传感器的长期漂移问题，本文提出了一种基于混合策略的电子鼻在线漂移抑制算法(online drift suppression algorithm for electronic nose based on hybird strategy，ODHS)。该算法结合主动学习和分类器集成方法在使用较少训练集样本的情况下，通过混合信息筛选标记少量测试集样本来更新分类器，获得相近甚至优于离线漂移补偿方法的分类精度。

本文提出的ODHS算法的创新点在于：

(1)初始分类器的训练只需要使用少量的训练集样本，减少对初始训练样本数量的要求。

(2)结合主动学习方法，在检测的过程中标记少量样本，大幅度提高检测的精度。

(3)结合分类器集成的方法，捕捉在线检测过程中传感器的漂移趋势。

1 相关方法

1.1 主动学习

主动学习(active learning，AL)作为机器学习的一个子领域，其核心思路在于以尽可能少的标注样本达到近似或者更高的识别精度。由于主动学习有选择地处理样本并与领域专家进行信息交互，近年来得到广泛研究。例如M. Goudjil等将主动学习与支持向量机相结合用于文本分类[6]。S. J. Huang等将主动学习用于深度卷积神经网络的训练中，该方法使用较低的成本实现有效的深度网络训练[7]。H. Xu等将主动学习中基于委员会查询方法与Tri-Training算法相结合提出QTB-ASVM算法，该方法用于解决支持向量机中标记样本不易获得问题[8]。

主动学习流程可以分为2个部分：初始化阶段和循环查询阶段。主动学习开始时，首先是通过少量有标记样本训练初始分类器，然后进入循环查询阶段，查询流程如图1所示。领域专家(S)按照一定的查询策略(Q)从未标注样本集合(U)中挑选满足要求的样本进行标记，标记完成的样本送入已标记样本集合(L)中，用于更新分类器。直至达到循环截止条件为止。如图2所示，主动学习方法按照待标记样本处理形式可以分为基于流式和基于池式两种，按照不同的采样策略也可以分为基于不确定性采样、基于委员会查询、基于模型变化期望等。

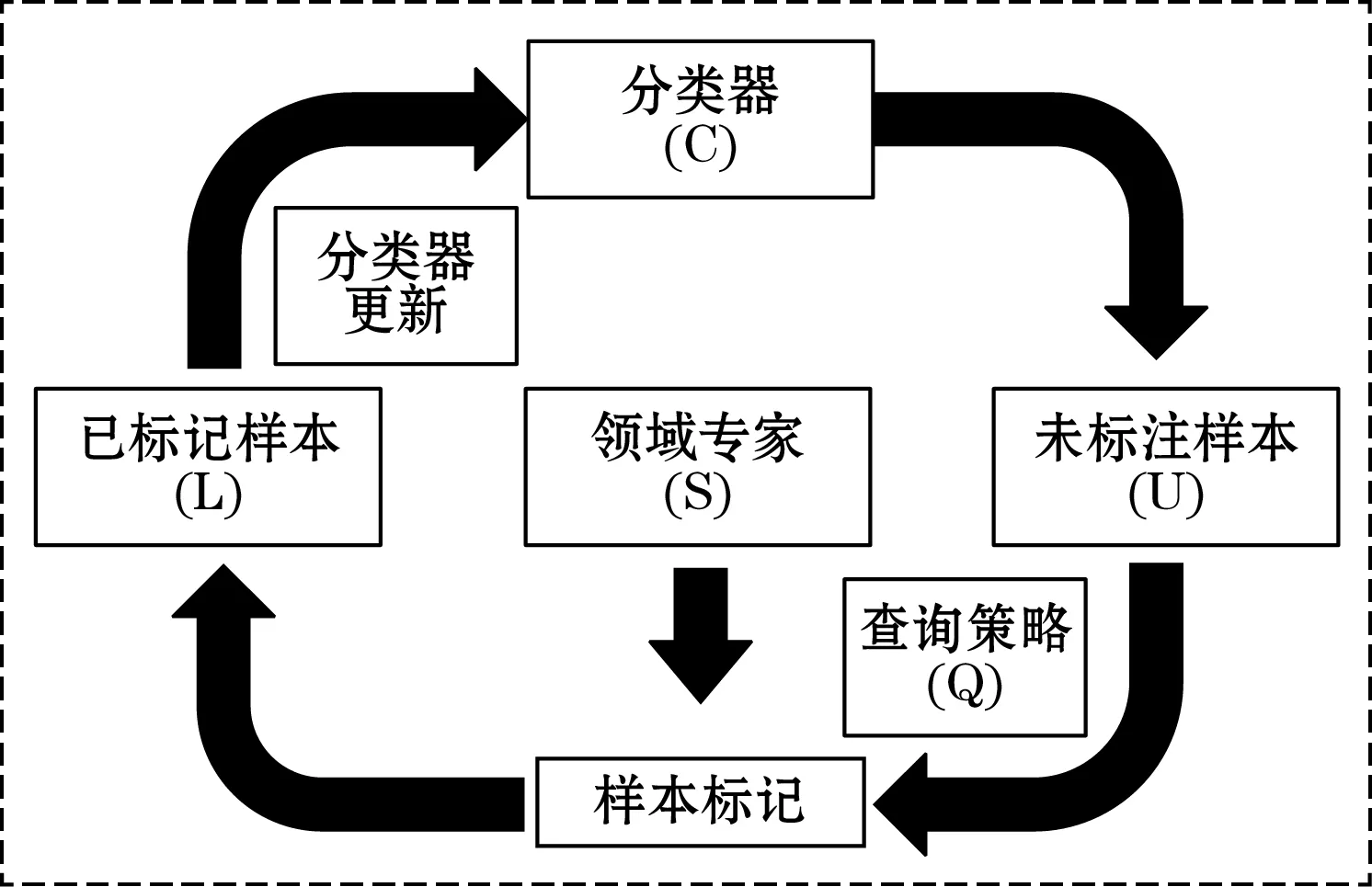
图1 主动学习流程

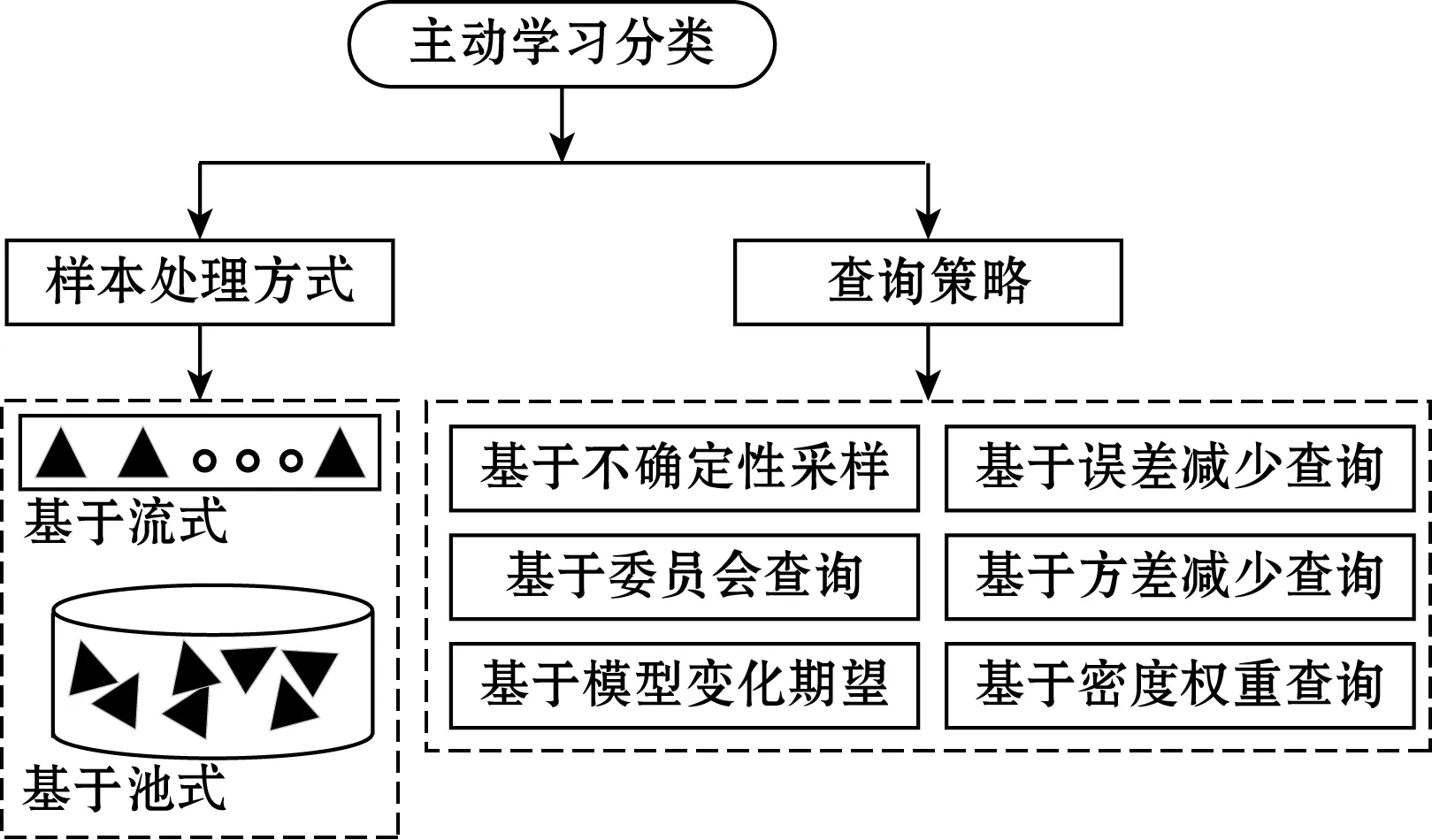
图2 主动学习分类

本文中主要涉及到的主动学习采样策略包括不确定性采样(uncertainty sampling，US)，基于委员会查询(query by committee，QBC)及其变体EQBC[9]。

US方法认为最不确定的样本最有利于提高分类器性能，通过分类器对样本的识别输出来衡量样本的不确定度，ODHS算法通过边缘熵(margin entropy，ME)来衡量样本的整体不确定度，如式(1)所示。

eime=-log[f(C1|xi)-f(C2|xi)]

(1)

式中：eime为样本对应的边缘熵；f(C1|xi)和f(C2|xi)分别为样本xi被分类为最大可能和次大可能类的概率，这种衡量方式会选择最大和次大概率最接近的样本用于专家标记。

QBC方法的核心是建立一个由不同分类器组成的分类委员会，而这些分类器之间需要存在一定程度的分歧。QBC方法中对样本的衡量方式主要有2种，分别是KL散度(kullback-leibler divergence，KLD)以及投票熵(vote entropy，VE)。本文提出的算法，采用KL散度来衡量内部子分类器对于样本分类的差异性。其公式如式(2)所示。

(2)

式中：eikl为样本对应的KL散度；K为分类委员会中分类器的数量；C为样本总的类别数；fm(Cj|xi)为样本xi被分类委员会中分类器m判定为类Cj的概率。

1.2 集成学习

分类器集成本质上是集成学习的一种。集成学习通过合并多个分类器的结果来完成学习任务，一般来说集成学习可以分为3大类：用于减少方差的Bagging，用于减少偏差的Boosting，用于提升预测结果的Stacking。按照分类器的生成方式又可分为串行以及并行生成方式。集成学习通过多分类器投票的方式，结合不同分类器的分类优势来提升集成分类器的分类精度。

2 ODHS算法

2.1 ODHS算法框图

ODHS算法整体框图如图3所示。其中分类器训练使用分类器集成方法。集成分类器包括内部的子分类器以及由子分类器整体构建的一个集成分类器。混合策略以样本的混合信息为基础，样本的混合信息包括混合熵以及样本的相似度信息。样本的混合熵包括样本的KL熵以及ME熵。样本的相似度信息主要指的是候选标注样本与训练集中样本的相似度。

图3 ODHS算法流程

2.2 ODHS算法说明

ODHS算法在分类器训练时共训练3个内部子分类器，对内部子分类器分别赋予不同的结果权重，并由此构成一个整体的分类器，如图4所示。用训练样本集整体、前半部分、后半部分训练3个子分类器C0、C1、C2，权重分别为W0、W1、W2。3个内部子分类器构成的集成分类器为C。考虑在实际的漂移过程中，当前漂移样本与在时间线上相隔越近的样本联系更密切，因此C2的权重应该比C1大，考虑到C0使用了所有的样本来训练，在分类的全局性上相比其他2个分类器更好，因此3个分类器的权重满足式(3)所示的关系。

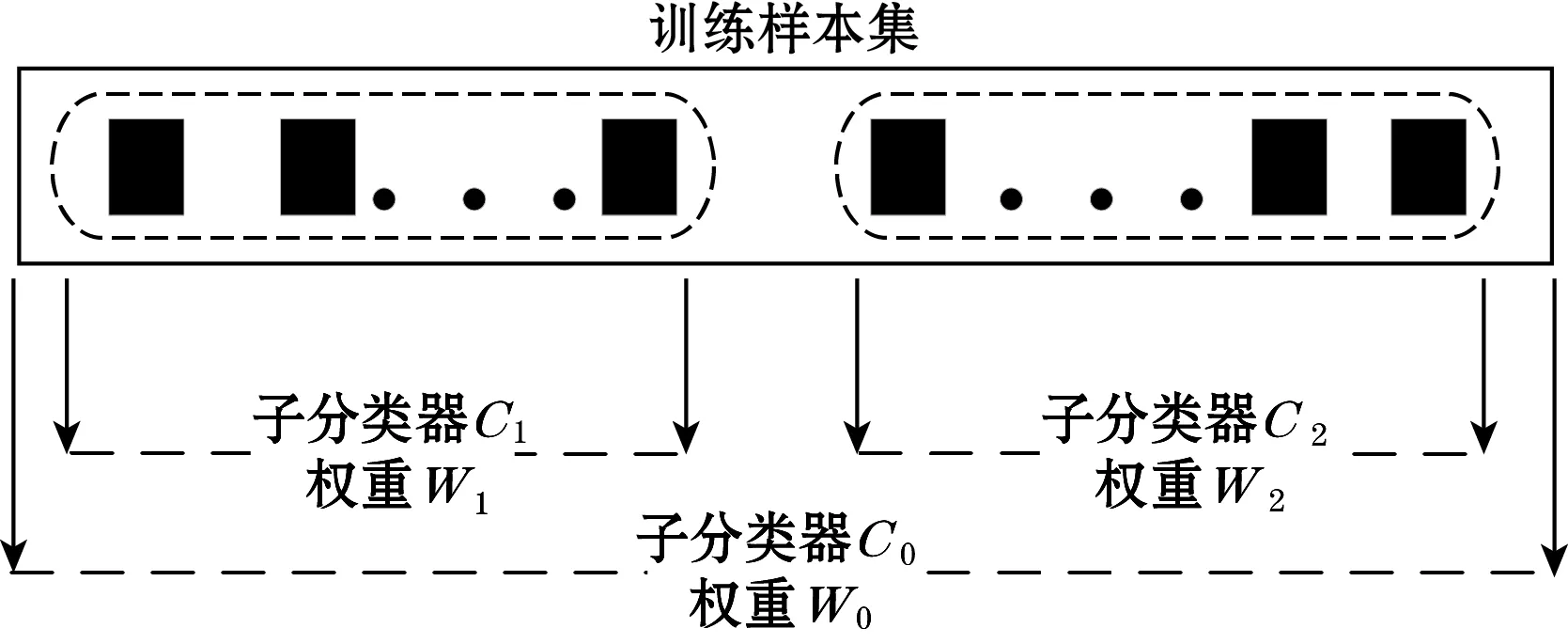
图4 分类器集成

(3)

对候选样本进行评价时不能只依靠集成分类器对于样本分类的不确定性或者内部子分类器对于样本分类的差异性，原因在于只考虑两者之一，则会存在忽略整体性或局部性的情况。表1、表2分别为实际实验的过程中通过MATLAB软件计算内部的子分类器及集成分类器对于样本A、B分类的结果。表1为内部子分类器将样本分为不同类的概率，表2为表1数据按照不同分类器的权重加权计算后得到。每一行表示单个分类器对某一样本分类结果，列表示该样本属于某一类的概率。

表1 内部分类器分类结果

表2 集成分类器分类结果

由式(1)、式(2)及表1、表2数据计算得到样本A、B的KL散度分别为0.012 5、0.009 6，ME熵值分别为1.074 1、1.086 1。按照KL散度则应选择样本A进行专家标记，按照ME熵则应选择样本B进行专家标记。因此综合考虑，将KL散度和ME熵值结合起来得到如式(4)所示的混合熵。

eikl-me=ω·noml_eikl+(1-ω)·noml_eime

(4)

式中：noml_eikl以及noml_eime分别为eikl和eime各自归一化后得到的；ω为KL散度的权重参数。

对于计算了混合熵的样本，采用局部离群因子(local outlier factor，LOF)进行离群点检测，检测后的样本，取前N个样本送入后续的相似性度量中。如果只是单纯的按照混合熵来进行样本的筛选，则忽略了候选样本与训练集中样本的相似性。如图5所示，其中实心代表训练样本，空心代表候选样本。在分类平面更新时，如果按照熵值来计算应该选择样本A进行标记，但是在训练集中样本A周围已经存在有与其相似的样本，考虑到样本之间的相似性，样本B在分类平面的更新上相对于样本A来说可能更好。

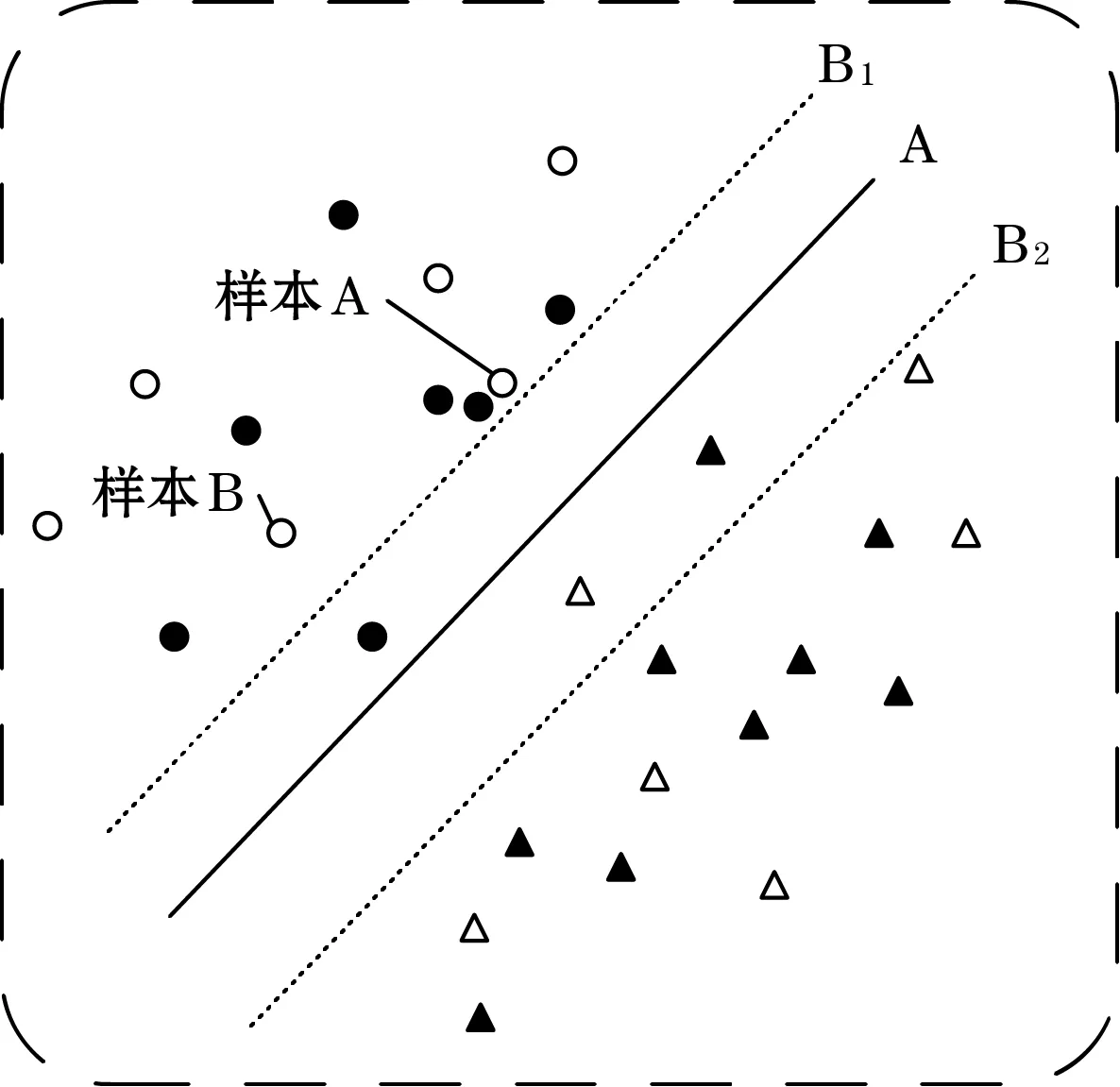
图5 分类平面更新

用余弦相似度来度量候选样本与训练集样本的相似度，从而解决样本的冗余性问题。其计算公式如式(5)、式(6)所示。

(5)

(6)

式中：L为训练样本集；n为训练集中与候选样本xi余弦相似度最大的前n个样本。

取这n个样本的余弦相似度的均值作为样本xi与训练集的相似度。因此样本的混合信息如式(7)所示：

eimix=α·noml_eikl-me+(1-α)·(1-noml_eisimi)

(7)

式中α为混合熵的权重，混合熵以及相似度在合并计算之前均需要先分别归一化。

根据得到的eimix，选择最大的前chooseN个样本用于专家标记。并将标记后的样本送入训练集用于分类器的更新。

2.3 ODHS算法流程

算法流程包括2个部分：初始化训练阶段以及在线检测阶段。伪代码分别如表3、表4所示。

表3 初始化阶段算法伪代码

表4 在线检测阶段算法伪代码

3 实验验证

3.1 实验数据集

实验所使用的数据集是来自于加州大学欧文分校的开源数据集[10]。该数据集是使用16个传感器构成传感器阵列，每个传感器采集8个物理参数。单个样本是一个128维的数据。该数据集通过3 a的采样，对乙醇、乙烯、乙醛、丙酮、氨气以及甲苯6种气体进行检测，共采集了13 910个样本。该数据集详细情况如表5所示。

表5 数据集详细信息

3.2 实验设置

使用Batch1样本集合作为训练集和验证集，其余的Batch2～10作为在线漂移检测的测试集。

实验的过程中对于Batch1中的445个样本，选择其中60个样本作为训练集，剩余的385个样本作为验证集。为了避免初始训练时出现类不均衡问题，因此60个训练样本是对于样本集中的6个类别分别取前10个样本。对于初始化训练阶段的阈值以及迭代次数分别设置为0.95以及10次。

在线检测阶段，在线样本池的大小设置为30，单次选择的样本数量chooseN设置为1，分类器的权重W0、W1、W2分别设置为0.58、0.15、0.27。KL散度的权重ω以及混合熵的权重α分别设置为0.21、0.77。使用SVM分类器作为基础分类器。实验中所使用的对比算法主要包括AL-US、AL-QBC、AL-EQBC、AL-ACR[11]，实验结果如表6所示，AL-ACR算法作者将Batch4，5以及Batch8，9分别合并后进行检测。

表6 平均分类准确率 %

表6中加粗数据是该批次样本方法分类准确率的最大值。其中AL-US，AL-QBC，AL-EQBC与ODHS在算法流程上是一样的，只是标记样本的选择策略不同。观察表6中可以发现在用约3.69%的样本作为训练集时，ODHS方法比AL-US、AL-QBC、AL-EQBC、AL-ACR在分类准确度上分别提高了5.2、6.2、2.8、6.6个百分点。综上可以发现ODHS方法对于提高在线漂移检测的准确度相比于其他方法效果好。

3.3 参数敏感度

对于实验的参数分析，选取单次采样的数量chooseN，KL散度的权重ω，混合熵的权重α进行分析。图6、图7是在保持其他参数不变的情况下，设置chooseN的范围为1～10，步进为1，得到的平均分类准确率及整体准确率的变化趋势。

图6 chooseN对平均准确率的影响

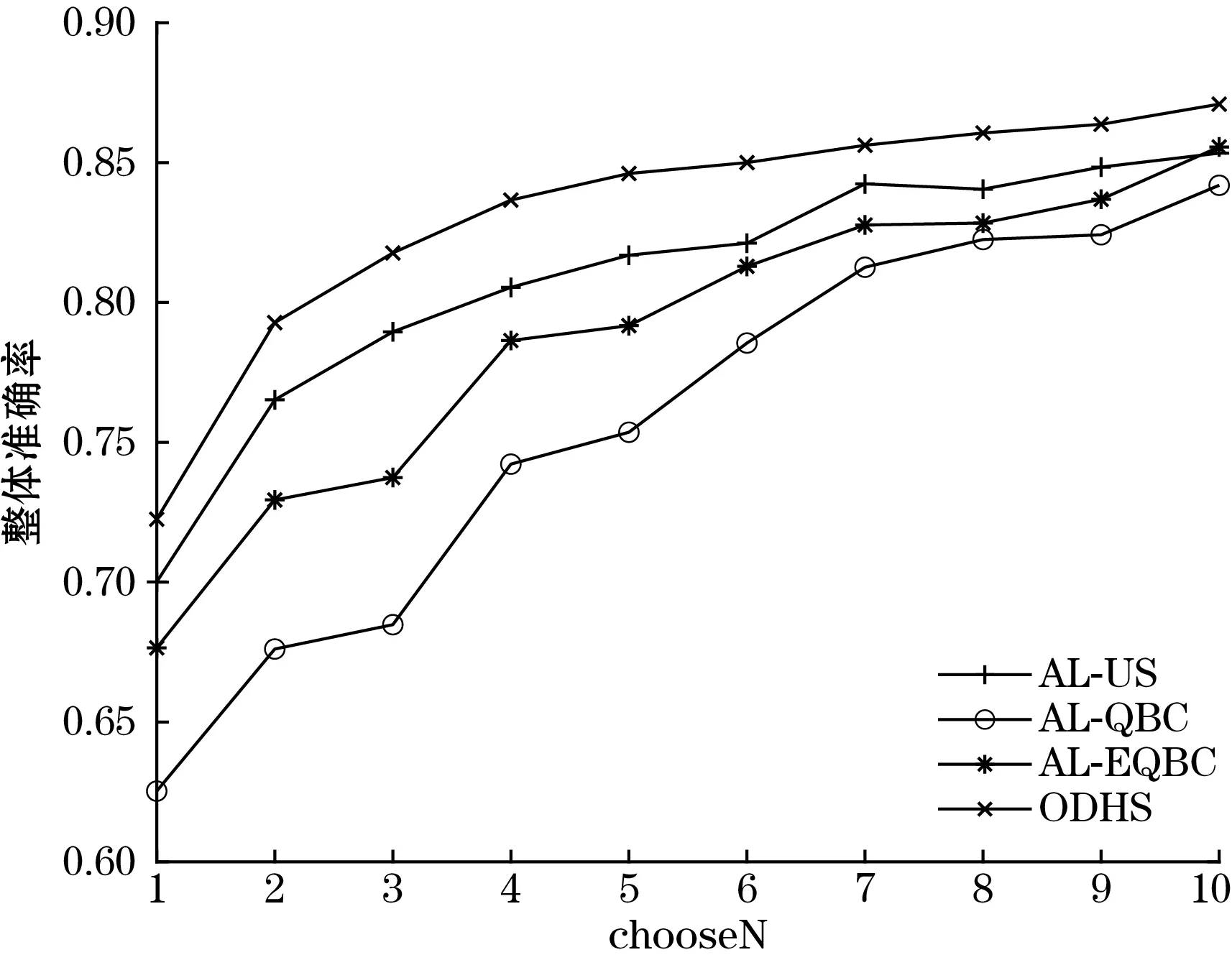
图7 chooseN对整体准确率的影响

由图6、图7可以看出，当单次选择的样本数量chooseN增加时，ODHS方法的平均准确率在chooseN为1～7的范围内一直最高，尤其是在chooseN从1升高为2时，对平均以及整体准确率的提高最明显。后期在chooseN为8时比AL-US平均准确率低，为9时与AL-US近乎持平，到10时则是4种方法中最高的。虽略有波动，但整体趋势仍为上升。除此之外chooseN的增加使得4种方法的整体分类准确率持续上升，且ODHS方法在这一过程中准确率一直是最高。平均准确率在后期出现波动，整体准确率在后期提高趋于平缓。可能的原因在于chooseN的升高，使得标记的样本数量上升，而这些样本之间仍然存在着信息冗余，导致分类器性能下降。

图8、图9实验均是在保持其余参数不变的情况下，对ω及α单一参数进行实验。由图8可以发现，随着ω的增加，整体准确率整体趋势是下降的，在ω为0.14～0.17区间内出现了较大值。平均准确率是先上升后下降，因此可以确定如果只由KL散度或者ME熵来评价样本均是不合适的，当ω在0.1～0.5范围内平均准确率以及整体准确率都有一个较大值。由图9可知，混合熵的权重α在0.7～0.9范围内，平均以及整体准确率均处于一个较大范围，且α在0.77左右时，平均以及整体准确率均处于一个较大值。因此也证明了将样本不确定性的混合熵与样本的相似性结合有助于提高平均以及整体分类的准确率。

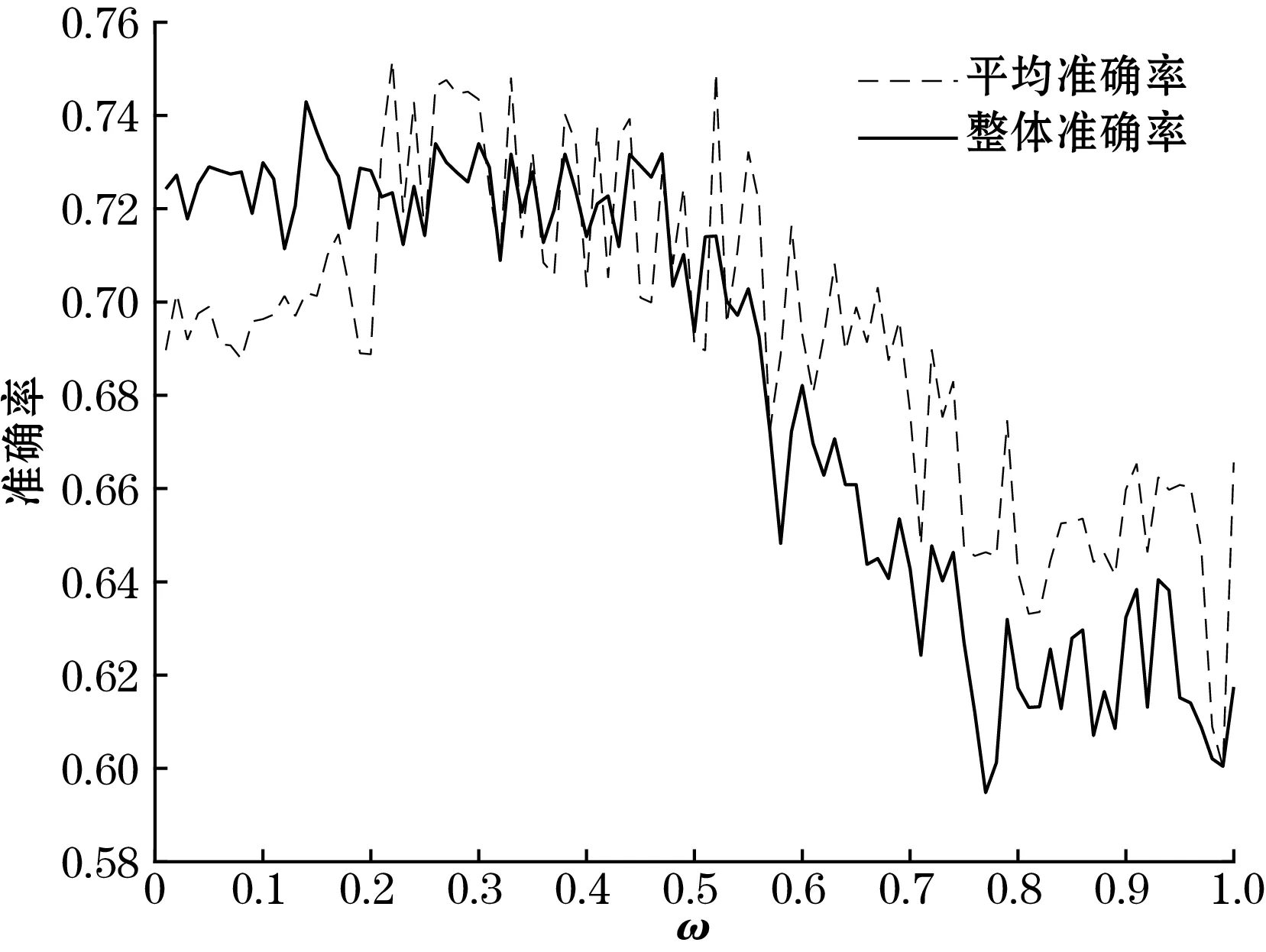
图8 ω对准确率的影响

图9 α对准确率的影响

4 结束语

为了解决电子鼻系统中存在的漂移问题，本文提出了ODHS算法，该算法用主动学习和分类器集成方法构建算法框架，然后在主动学习中充分考虑内部子分类器以及集成分类器对样本分类的意见，并结合样本相似性度量，从而选择对于提高分类准确率更有效的样本。实验证明相对于其他方法，在使用少量训练样本的情况下，该方法仍能取得一个较好的精度。但是在采样过多的情况下，该算法对于分类准确率的提高幅度逐渐降低。后期的工作将改进ODHS算法，使其在采样数量增加时能继续大幅提高分类准确率。