基于声速追踪的超声波液体流量计量方法

赵楠楠，徐安察，胡 亮，付 新

(1.浙江大学流体动力与机电系统国家重点实验室，浙江杭州 310027，2.浙江启尔机电技术有限公司，浙江杭州 311305)

0 引言

超声波流量计因其高精度以及非接触的特性，在行业得到了广泛的应用。在流体测量中，基于超声波的计量方法有多普勒法、互相关法和时差法等[1-3]。其中，时差法应用最广泛，特别适用于小口径、低流量且有超洁净需求的工业半导体产业。

声波在介质中的传播时间主要通过分析接收的声信号获得，因此，声信号的质量对基于时差法的流量传感器计量精度有着较大的影响。为了提高接收端声信号的信噪比，很多学者在流场和声场耦合方面进行了广泛的研究[4-7],为传感器基础架构设计提供了有效的指导方案。在声信号信噪比达到可计量的标准后，工况环境的变化会对声信号的幅值造成影响，这对常用基于阈值法计算声学传播时间的方案有着较大的影响。声波幅值变动超过一定程度会导致预先设计好的固定阈值提前或者延后触发，继而导致计算的声波传播时间与实际相差一个或多个声信号周期，这种现象称为跳波。不少研究提出了抑制这一问题方法。汪伟等[8]将阈值比例系数基本不变作为前提，提出了可调阈值法，毛凯等[9]提出了一种自诊断双阈值法，Z. Fang等[10]以声波的物理特征为切入点，提出了一种有效的超声波信号起振点判定方法。基于以上的研究方法，在一定程度上能够识别跳波，减少其造成的流量计算误差。

在实际使用中，在稳定获取声波传播时间的基础上可进行相应的流量计算。基于时差法的超声波流量计算，从计算原理出发，除声波传播时间外，还包含流体介质中的声速。由于介质中的声速会随温度和压力变化而变化[11]。因此，在计算中通常会考虑避免使用声速，更加倾向于仅使用声波的上/下行传输时间来计算流体流速[12]。或者当温度是影响计量的主要因素时，可考虑进行相应的补偿。如，杨志勇等[13]基于实验数据，建立了介质声速和温度之间的关系，以此作为基础对不同温度下的计量数据进行修正。L. Ge等[14]基于金属热膨胀和温度的关系，将声学传感器置于特殊金属样件上来获取温度信息，继而对流量数据进行修正。

综上所述，需要通过温度传感器或者类似的方式来获取温度信息来完成相应的数据修正。由于温度等因素造成介质中声速的变化，且需测量这些因素，并以此对流量进行修正，则会增加流量传感器在设计和应用上的困难。为了克服这一困境，文中从超声波测量的基本原理出发，说明了声速与声波渡越时间之间的联系，并给出了基于声速变化对流量修正的方法。文中介绍了超声波测量常用计量方法的原理，并由此引出了文章提出的流量修正方法。 并在下文中给出了相应的实验数据和对比结果，对该方法进行了验证。

1 方法

1.1 传统时差法介绍

如图1所示，时差法超声波流量计是通过安装在测量管上、下游的换能器T1和T2发射和接收超声波信号来获取其在介质中的传播时间，然后基于传播时间差值计算介质的流速或者流量。

图1 时差法测量原理

如图1所示，基于超声波时差法原理测量流速的基本公式如下所示。

顺流渡越时间为

(1)

式中：L、c和u分别为声程、介质中声速和介质流速。

逆流渡越时间为

(2)

声波渡越时间与声程、声速和介质的流速均有关联。理论上，当c和L为常数时，渡越时间td和tu仅与u有关，可得顺逆流时间差如式(3)所示：

(3)

待测量液体介质的声速范围是1 100～2 200 m/s，对于内径d=6 mm的测量基管，设定满量程8 L/min的超声流量传感器，介质最大平均流速不超过4.71 m/s，满足c2>>u2，式(3)可简化为

(4)

由此可获得流速为

(5)

式(5)为时差法超声波流量计测量的基本公式，在理想情况下，可由测量得到的时间差计算出测量基管内介质的流速。但实际工况下，声速会因介质的改变以及环境因素(如温度)的影响而改变。因此，为了提高流量测量的稳定性，会对这些变化进行补偿，为了减少声速的影响，传统的补偿方法是消除声速c[15]，通过式(1)和式(2)的倒数之差消除声速，如式(6)所示：

(6)

继而得到流速：

(7)

观察式(7)发现，计算过程中主要涉及tu和td，虽然通过数学变换的方式消除了c。但由式(1)和式(2)可知，tu和td无法规避声速c的影响。

1.2 建立流量计算模型

考虑顺逆流时间和：

(8)

由式(8)可得：

(9)

结合式(8)和式(3)可得到tu和td与∑t和Δt之间的关系：

(10)

(11)

将式(9)、式(10)带入式(7)可得：

(12)

由于c2>>u2，∑t2>>Δt2，继而式(12)可以变换为

(13)

由式(8)和式(3)的比值同样可以得到式(13)，考虑式(13)是一个计算流量比较合理的形式。因此，以参考式(13)的形式，建立如下的流量计算函数：

(14)

式中：a1、a2和a3为待拟合系数；k0为特定声速c0下的待拟合系数。

基于该模型可计算一些实际工况中声速变动较小的流体的测量。以流体介质是水为例，可建立能够容纳水温10～90 ℃变化的流量计算模型。水中温度和声速的关系如式(15)所示[11]：

c≈1 404.3+4.7T-0.04T2

(15)

式中T为温度，℃。

由式(15)可知，10～90 ℃的温度变化对应水中的声速变化是1 447.2～1 550.4 m/s。

基于图2所示的测试平台，可获取求解拟合参数所需的原始测量数据。其中，标定设备可采集实际的流量值，数据采集主控电路可获取超声波的渡越时间相关数据。处理和分析不同水温下获取的原始数据并进行相关拟合，计算出合适的参数后可获得图3所示的拟合结果，由此获取设定条件范围内的流量计算模型us(Δt,∑t)。

(a)流量标定设备实物主体

图2 数据采集实验平台

图3 全温度全流量下的us(Δt,∑t)拟合结果

此外，可通过表1所示的参数，来检验计算模型是否符合设计要求。

表1 us(∑t，Δt)与实测流量一致性参数

表1中，SSE为和方差，越趋于零则拟合结果越好；RMSE为均方根差，效果同SSE；R-square为“确定系数”，通过数据的变化来表征一个拟合的效果，其正常取值范围为0～1，越接近1则表示计算模型变量对预测数值的解释能力越强。

1.3 声速追踪参数

上文通过改变水温获取一定声速范围的数据，并以此为基础建立了特定声速或一定声速范围内的普适性计算模型，无法从本质上改变因声速改变而造成的计算误差，最佳的解决方案是在流量计算过程中，能够自适应追踪声速变化，并进行相应的流量补偿计算。

us(Δt,∑t)涉及∑t和Δt2个主要变量，具体的变化形式可从式(3)和式(8)中获得，当满足c2>>u2时，参考介质中的顺逆流传播时间差Δtr可表示为

(16)

式中cr为建立计算模型过程中使用的参考介质(如25 ℃水)的声速。

同理，顺逆流时间之和∑tr可表示为

(17)

定义系数k为

(18)

式中c为当前待测量流体介质中的声速，通过对比式(3)、式(8)与式(16)、式(17)可知：

Δtr=k2·Δt

(19)

∑tr=k·∑t

(20)

式(19)和式(20)的变换，可将目前待测的流体中得到的∑t和Δt转换为us(Δt,∑t)中的∑tr和Δtr。由此，可将不同声速下的待测量介质流量计算统一归纳到基于参考介质获取的计算模型us(Δt,∑t)中，进再行计算。由此补偿因声速变化导致的流量计算误差。

该方法的关键是获取转换系数k，cr是参考介质的声速，具体数值可通过测量等方法确定。当前测量介质中的声速，则可以通过∑t来获取。通过式(8)可知，在c2>>u2且声速一定时，流速u的变动对∑t的影响基本可以忽略不计，且有

(21)

图4 的关系曲线

∑t依赖于准确获取顺/逆流下的渡越时间tu和td，这点可以结合陈洁等[16]提出了双阈值法和Z. Fang等[10]关于声波首波计算的相关研究来提高其稳定性。基于双阈值法，得到图5中序号为2、3和4的3个过零点，考虑波形幅值较大时过零点更加稳定，因此可选择较靠后的过零点作为计算渡越时间的参考点。例如，选择阈值触发后的第2个过零点(对应图中的序号3)。当然阈值触发也有相应的弊端，当工况环境变化等因素导致波形幅值变化时，可能引起跳波的问题。此时，可通过声波物理意义上的首个起振点(忽略淹没在噪声中的声波)，即以首波作为参考点计算渡越时间，在一定程度上可避免跳波的影响。

图5 关于∑t的计算方式

从理论出发，∑t是通过声波在介质中传播的顺/逆流渡越时间计算得到的。而实际测量中，额外包括了硬件电路延迟、压电传感器以及声波在管壁中消耗的时间。

因此，计算之前需要先减去声波收发整个过程中非测量介质中消耗的时间tdelay，显然tdelay是比较稳定的，不因待测量介质中声速的变化而变动。因此，可使用参考介质中的数据进行计算，将获取的∑tr减去声波收发过程在参考介质中的理论传播时间以及2nT0，即：

(22)

式中：T0=1/f0；f0为压电片的激发频率；n取决于计时参考点的选择。

若选择首波之后的第2个过零点作参考点，则n=2，则k可通过式(23)获取：

(23)

式(23)即可表征介质中的声速变动，计算出k后，可通过式(19)和式(20)将待测量介质中的参数映射到基于参考介质获取的流量计算模型us(∑t,Δt)中，最后完成流量的修正计算。

最后，通过顺逆流波形幅值数据，基于经典的互相关法[2]计算Δt，通过式(24)计算偏移量

(24)

式中：i为窗口选择求和互相关的数据范围，α≤i≤β；Su为逆流波形幅值的数据；Sd为顺流波形幅值的数据；τ为数据偏移量。

相应的数据计算结果如图6所示，图中S为波形幅值，互相关系数R(τ)最大值对应的偏移量即为顺逆流的时间差Δt，可通过插值法提高时间上的分辨率。

(a)顺逆流波形幅值

(b)顺逆流波形互相关计算结果图6 互相关法计算

2 实验验证

由于实验条件和半导体行业中常用的各种化学介质使用环境的限制，文中实验介质以水为主，实验测试台及原理示意图如图7所示，通过在线加热器调控水温，模拟声速的变化，水中的声速与温度的关系可参照式(15)。在保持传感器所在回路出入口压差Δp和阀口面积A不变时，参照阀口流量公式：

图7 实验测试台

(25)

式中：q、Cq和ρ分别为流量、流量系数和水的密度。

Cq不变时，由于ρ的变化，25 ℃相比于80 ℃时计算得到的变化约为1.28%(该数值可查找不同温度下水的密度计算得到)，以该值作为参照，可假定温度变化后，实验机台基本维持稳定的流量。

实验中记录了温度由25 ℃升高到80 ℃主控电路采集到的声波传播时间，结果如图8所示，其中tu和td分别代表逆流和顺流下的声波渡越时间。实验中随着温度升高，声速由1 496 m/s逐渐变化到1 555 m/s(过程中声速变化约为59 m/s)。在线加热器进行温度调控时，引起的温度波动造成了图8中呈现的时间振荡。

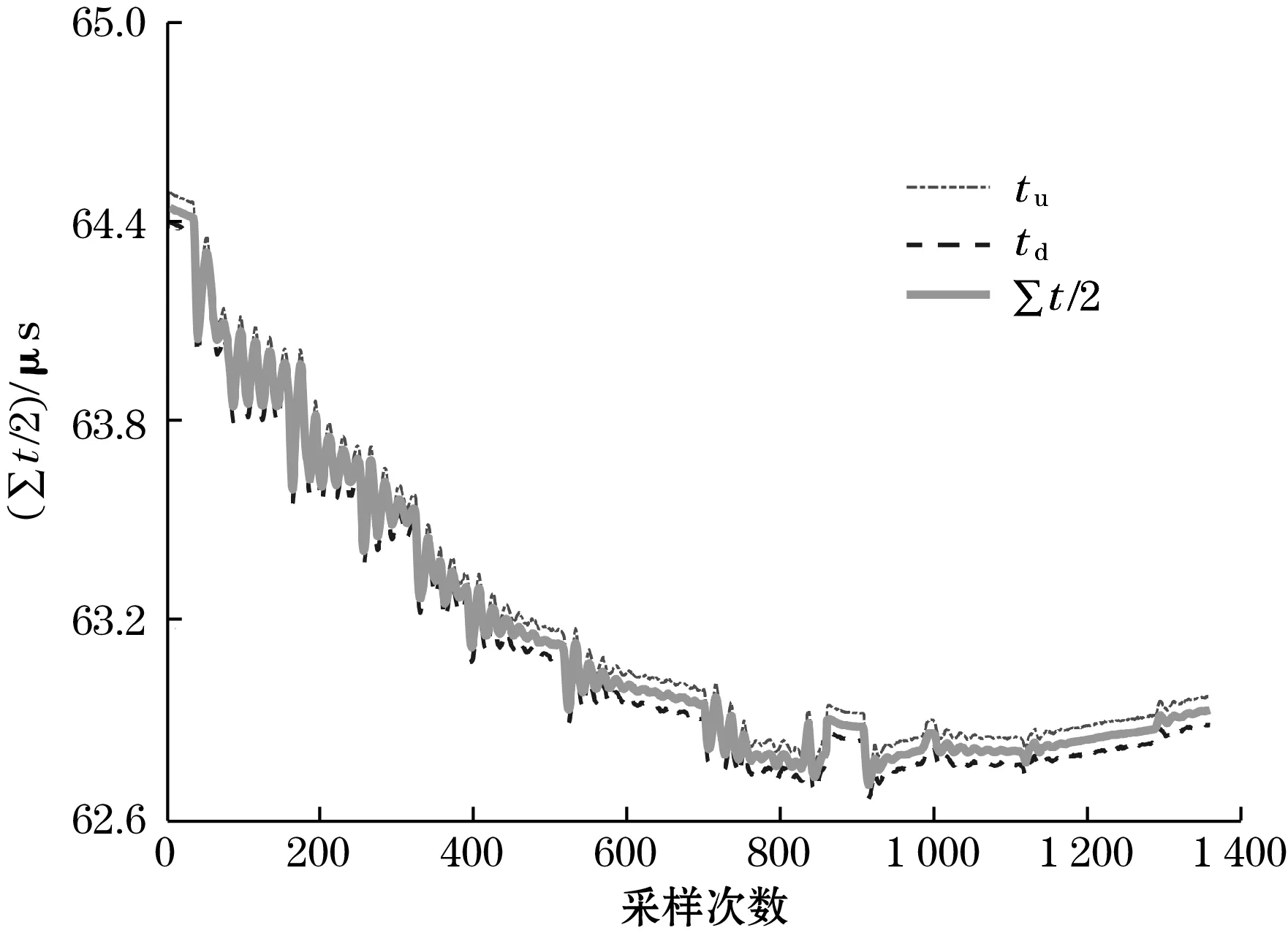
图8 声波传播时间

若采用多个温度数据建立式(14)形式的流量计算模型，则计算的流量模型在一定程度上会抑制温度对流量的影响，因此文中使用声波顺逆流传播时间差Δt作为主要测试数据。

结果如图9所示，图中显示了原始时间差和式(19)修正后的时间差。两者的变化趋势也在图中显示，原始时间差数据呈现出明显的变化趋势，而修正后的数据能够保持相对的稳定。从数据分析可知，原始的Δt变化趋势曲线的终值/初值是80.2/84.405=95.02%，而经过修正后同样的比值是82.348/83.1447=99.04%。即升温前后，原始Δt相较于初始温度下的数值变化了4.98%，修正后的Δt相比初始值变化了0.96%，由此可知，通过式(19)修正后的Δt，可在一定程度上补偿因介质声速变化对流量计量造成的影响。

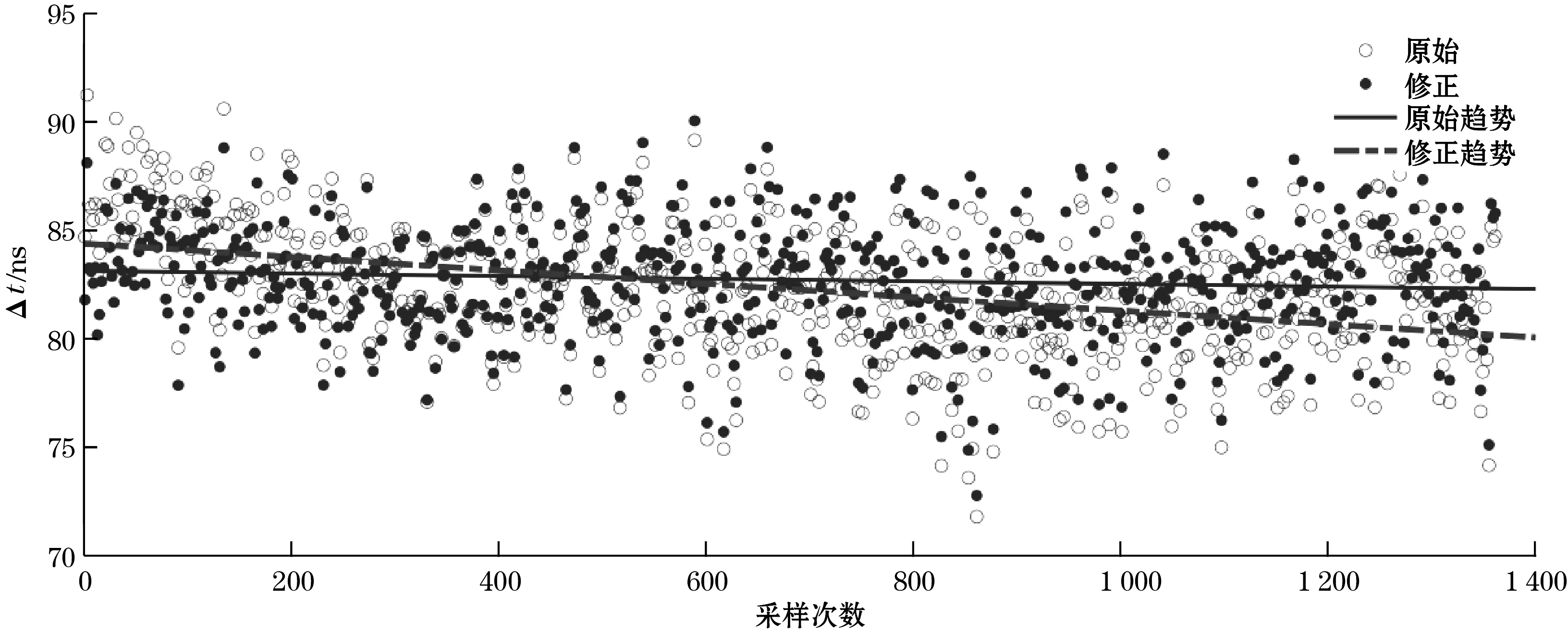
图9 互相关法计算Δ t

3 结论

待测量介质声速的变动对基于超声波方法的流量计量仪器有着较大的影响。半导体产业中使用的介质种类繁多，声速基本分布于1 100～2 000 m/s范围内，对特定介质(如25 ℃水)中标定的超声波计量仪器而言，若不进行流量修正，流量测量偏差会随着待测介质声速与标定介质声速差异的增加而增大。且在不更换介质的工况下，受到环境因素(如温度)的影响，声速也会发生一定的变化。针对这一问题，文中通过声波的传播时间追踪声速变化，并在此基础上提出了流量计算的补偿方法，继而有效抑制了介质声速变化对超声波方法计量液体流量的影响。提高了液体超声流量传感器流量计量的稳定性和可靠性。