用『多维度量原理』破除『单位相乘』论
——关于量感前提下数学运算中法理一致性与正确性的思考
2022-11-01郑大明
文 郑大明
在小学阶段的数学学习中,度量单位是广泛应用的基本测度标准。但在日常教学中,关于计数和计量单位的教学,存在一定的认识和操作误区。比如有学者在论文和讲座中也提出“单位×单位=新单位”的观点,并且运用等式的性质形式化地“证明”了小数乘除法中的通用算理是“单位乘单位等于新单位”。然而,经过搜集、查找度量单位的产生历史和研究度量的本质后,发现这个提法有待商榷。
本文拟从以下几方面剖析度量单位的建立与应用,厘清其在计算教学中的一些基本认知,确保数学运算中法理推演的一致性与正确性。
一、度量理论的基本内涵
度量触及数学的本质,是贯通数量关系和空间形式的桥梁,它是人类认识、理解和表达现实世界的重要工具。度量的本质就是测度和计算数量的多与少。量感作为核心素养,重点是培育学生对于事物可测属性及大小关系进行定性描述和定量感知的基本能力。其核心价值在于形成度量意识,理解和掌握度量方法。因此,我们必须弄清楚度量的基本常识如量态、量标、量程、量具、量值等度量概念的基本意义和操作办法,避免在组织学生进行度量感知、计数与计量运算等活动时出现不必要的误导。
1.量感是指对事物可测量属性及相互关系的感知。
感知,就是感觉和知觉的合称。通常把言语方式的感知称为抽象感知,非言语方式的感知称为直观感知。所谓直观感知,就是人们对事物、现象等感知对象通过看、听、摸等活动获得其所需要信息的过程。因此,义务教育阶段的量感目标主要是对量的直观感知,也就是要让学生看到、听到或者触摸到事物的可测量属性,比如事物的轻重、多少等,并通过其大小关系,抽象感知事物的个数、倍数等度量属性。
2.量态是指事物的可测量属性的确定样态。
所谓量态,就是指事物或现象的可测定属性的基本样态,也就是对事物可测属性的定性刻画。比如,一个人,他的身高即长度、体重即质量、个头即体积、力气即力量等具体的可测属性;还有学习能力、工作能力、创造能力等抽象的属性。
具体可测属性,我们可以借助尺子测身高、磅秤称质量、体温计测温度等,测量结果确切,精准度高。这种直接或间接使用工具方式进行的度量样态,通常叫做具象度量。
非具体可测属性,我们可以采用考试、问卷、做项目等方式用打分量表的方式来度量,度量结果相对确切,但模糊性较强。还有如事物的价值指标等需求属性,完全是约定和协商而得出度量结果的。比如一只玉镯的单价、自由市场白菜的单价等。这种以评估、协商、约定或者规定等运用思维和意识方式进行的度量样态,通常叫作抽象度量。
3.量标是指度量事物可测属性的约定标准。
测量事物的不同属性,就需要使用不同测量标准。计数或者计量的标准统称度量标准,又叫作一个度量单位。一般情况下,具象度量通常以实物的标本或局部量作为单位,如长度、面积、重量、电量、时间等。抽象度量往往以设定数值或者确定分值指标等作为单位。比如十进制计数单位个、十、百、千;人民币单位元、角、分等。
目前,除了各国规定的测量标准外,还出现了统一的“国际单位制”,如长度l“米制”、时间t“秒制”和重量m“千克制”等。
4.量程是度量事物可测属性的维度和程序。
同一个事物,可以度量的属性很多。到底应该度量事物的哪些属性以及如何度量,完全是根据实践的需要和研究的任务来确定的。由于不同学科、不同行业度量的目的、手段和方法是不一样的,因此就产生了不同性质、不同次数、不同方向等的多维度量。
在小学数学教学中,可参照的度量原理(如下表1)值得我们关注。下面只就其中的度量维度做简单的说明。
所谓度量维度,是指被测量事物的几个属性或者测度的方向与步骤。
零维度量:测量事物站位的存现状态这一属性,即这个东西在哪里,出现几次或者占几个位置。如“数三只羊”,只关注出现一只羊就需要占据一个空间位置,三只羊占三个位置,因此需要按频率数三次。不关心每只羊的高矮、重量、年龄等可度量属性。几何特征就是“3 个点”。测量标准则抽象为自然数基本单位“1 次”,简称“1”。当所有事物和现象我们都只关注它的呈现频率时,就抽象为“零维”的位置记录属性。
一维度量:度量一个事物的某一个可测量属性。如“一只羊的肉可以切成几块来等分。”这就是一个度量维度,按“块数”切分一只羊。如果一只羊的肉切成10块,它的度量标准就是“1 块”,度量结果就是“1 只羊的肉=10 块羊肉”。几何特征就是“一条10 等分线段中的一段”,表示一块羊肉是整只羊肉的十分之一。这里度量标准就抽象为按“1 块”计数,然后数出对整只羊进行等分后的块数。这时用到的度量单位是具象的单位“1 块”,复合表示为“只/块”。
二维度量:同时度量一个事物的某两个属性或者连续两次度量事物的同一属性。如“一只羊可以等分成几块,一块可以等分出几斤。”这就是两个度量维度。它的度量程序是先按照“块数”等分一只羊,再按照“斤数”等分一块羊肉的质量。如果一只羊等分成10 块,再等分称出10 斤,它的度量标准就是“1 块”和“1 斤”,度量结果就是“1 只羊的肉=10 块羊肉=100 斤”。几何特征就是“一个正方形等分为100 份中的一份”。可以理解为先x 轴方向10 等分,再y 轴方向10 等分,一共将正方形100 等分。表示一块羊肉是整只羊肉的十分之一,一斤羊肉是一块羊肉的十分之一,也就是一斤是整只羊肉的百分之一。测量标准抽象为先按“1 块”再按“1斤”对整体事物进行二次等分后进行数数。这时用到的度量单位是具象的单位“1 斤”,这里复合表示为“只/块/斤”。
多维度量:同时度量某一事物的三个以上属性或者连续三次以上度量事物的同一属性,就称为多维度量。其度量规则就是按照零维、一维、二维的规律以此类推进行理解。其维度的多少是按照度量的需要来确定的。比如“一斤羊肉可以装几袋”“一袋羊肉含多少克蛋白质”等,都是我们可以类比思考和操作的。

表1 多维度量原理示意表
5.量值是度量事物的频次和结果的定量表征。
所谓量值,目前存在两个基本意义。一是表示度量的基本单位与导出单位之间的比率关系,也就是“进率”。如1 百÷1 个=100;1 分米÷1 米=0.1,1 平方分米÷1 平方米=0.01。二是表示被测事物度量结果与标准单位的比率关系。如长方形的长5 米,宽3 米,它的面积:1 平方米×3=3 平方米,3 平方米×5=15平方米。二次度量结果与标准单位的比率为“15 平方米÷1 平方米=15”。这里的100,0.1,0.01,15,计量学上均称为量值。
计数单位的量值根据使用规则确定。如十进制记数单位之间的量值按位置数确定计数标准:个位标准“1”、十位标准“10”、百位标准“100”、千位标准“1000”。其他如二进制、十二进制、百分制等,均按具体需要进行规定。
二、多维度量的基本原理
1.量标建立的手段:约定与法定。
在原始阶段,人们用结绳计数、用身体量物、用脚步测量、以物易物等,实现了一定的商品流通和物资交换的需要。这时,度量的标准,就是生活在一定社会群落的人们约定怎么计量,相对统一就可以了。
然而,随着商品流通和物质生产范围不断扩大,各自约定的度量标准不统一,影响物资生产技术的标准性和商品流通的公平性。于是就出现了“秦始皇统一度、量、衡”案例,让秦国各地在计量物体长短、容积、轻重上有了标准的度量准则,给当时的商业和经济发展提供了便利。
如今为了满足世界技术标准和商品流通,各国在保留自己的度量标准后,法定使用了“时间、长度、重量、电流”等国际单位制,比如基本单位“秒、米、千克、安培”等。
2.量标推演的原则:导出和转换。
在具体生产和流通领域,只有基本单位还不能满足需要。因为只用基本单位测量时,量值太大或者太小,不方便交流。于是人们在基本单位上进行了扩展,采用导出法和转换法,创造出一系列新的单位。
(1)一维度量单位的导出。
度量事物的一种属性,我们称为“同类量”度量。“十进制计数法”的新单位导出算法是:基本单位“1”乘进率“10n”。土地或平面的面积计量的新单位导出算法是:基本单位“1m2”乘进率“100n”。
(2)二维度量单位的转换。
●同质度量的单位转换。
所谓同质度量,就是多维度量时,都是度量事物的相同属性。比如加、减、乘、除法。计算中都是在数数,由于数的增加,不断更换较大或较小的单位(如图1)。计算度量面积和体积,都是度量长度,但是单位就需要转换(图2)。
例1.十进制计数法的计数单位转换。
“9+3=12”,第一次度量数“9个1”,第二次度量数“3 个1”。合并时“9+1”换成新单位“十”表示,余下的“2”还是原单位“1”。类比得出:“90+30=120”“9 米+3 米=12米”“90 吨+30 吨=120 吨”。

图1
看图视角:加法从上往下看,减法从下往上看。
“9×3=27”,第一次度量得出“9个1”,第二次度量得出“3 个9”。合并时“3 个9”转换成“2 个10 和7 个1”表示,也就得到“27 个1”。
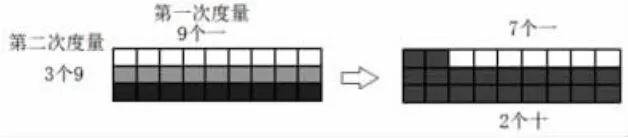
图2
看图视角:乘法从左往右看,除法从右往左看。
我们从基本度量单位看,两次度量的基本单位“1”没有变化,只是度量单位的对应的量值在累加。
“9+3”:9 个1 加3 个1 得12个1。
“9×3”:9 个1 连续加3 遍得27 个1。
在小数和分数的计算中,同质的大小不同的度量单位,可以通过进率规则对一个单位进行累加或者细分,不断导出和转换使用新单位参与计算(如图3)。

图3
例2 .小数和分数的计算,分别由基本单位“自然数1”导出“十分之一”和“百分之一”参与计算。
“0.2×0.4=0.08”:根据结合律将算式拆分为“(1×0.1×0.1)×(2×4)”。
第一次度量,1×0.1 理解为把自然数单位‘1’等分为10 份,得到新单位“1”的十分之一。
第二次度量,把新单位“十分之一”再等分为10 份,得到最新单位“1”的百分之一。
第三次度量,相当于2 个百分之一连续取了4 次,一共取了8个百分之一,得到百分之八。
看图视角:乘法从左往右看,除法从右往左看。
例3.面积测量计量单位转换。
“长方形长9 米,宽3 米,面积3×9=27(平方米)”。第一次度量边长9 个1 米,对应9 个1 平方米;第二次度量边长3 米,对应3个9 平方米。所以“1 平方米×9×3=27 平方米”。
我们从基本度量单位看,两次度量的基本单位没有变化,只是度量单位的量值在累加。
第一次度量,长度单位选用的“1 米”,量值对应9 个1 平方米。
第二次度量,长度单位选用“1 米”,量值对应3 个9 平方米,连加三遍得出27 个“1 平方米”。
同理得出:计算物体的体积,也是用基本单位“1 立方米”与长度的对应关系计算出体积的度量值。
●异质度量的单位转换。
所谓异质度量,就是对事物相关属性的多维度量。比如购物需要价格与数量,开车需要度量路程和时间,用电需要度量功率与时间等。有时我们就用复合单位表示,有时又会使用新的度量单位表示。
例1.妈妈购买了5 斤苹果,用了20 元。每斤多少元?
第一次度量付钱20 元,度量单位是“1 元”;第二次度量称重5斤。如何知道每斤的单价呢?就按照斤数第三次去度量钱数。按斤数等分20 元,得出“20÷5=4(元/斤)”这里的单价就是复合单位。小学算术里面不写复合单位,转化为用“元”替代书写,答语写“每斤5 元”。
例2.小王家有4 个空调,每个3500 瓦。一天,他们家开了6小时空调,用电多少度?每度0.52元,要花多少钱?
第一次度量4 个空调。总功率是3500 个1 瓦,连加4 次得14000 瓦也就是14 千瓦。
3500×4=14000(瓦)=14(千瓦)
第二次度量4 个空调开了6小时,也就是14 千瓦要连续加6次得出84 个“千瓦·小时”。因为“1千瓦·小时”是复合单位,为了方便记录,使用新单位“1 度”记录。
14×6=84(千瓦·时)=84(度)
第三次度量,每度电0.52 元,84 度的价钱就是0.52 元连续加84 次得出43.68 元。
0.52元/度×84 度=43.68元
三、结语:度量标准的唯一性保证运算推演的一致性
1.由于量标的独立性和唯一性,所以单位本身不能运算。
由于量态的不同,事物的可测属性和度量标准是具有独立性和唯一性的。如自然数的“1”、时间的“秒”、质量的“千克”等是专门约定的,单位与单位之间不能相互推演。即使是“个、十、百、千”这类的单位,也是唯一的个体。因为每个单位都没有第二个,所以就不会出现“十减十等于零”“百乘百等于万”的现象。
在物理量计算中遇到复合单位,即以二维度量使用不同属性的测度标准,有些可以换成新单位表示。如电功率单位“伏特·安培”用“瓦特”表示。土地丈量的面积单位,比如因纵横两次使用长度单位“米”度量正方形或者长方形,因此换用“1 平方米”的标准正方形作单位。
所以,“单位乘单位等于新单位”的说法是错误的。
2.由于量值的可加性和可分性,所以单位可以参与运算。
由于同质单位和导出单位之间有量值(进率)关系,决定了它们可以组合与分解,即可参与计算。
比如“一”与“二分之一”的关系是“两个二分之一组成一”,量值(进率)是2,所以1 个二分之一加1 个二分之一,得2 个二分之一,就可以换成“一”表示。
比如长3 米和2 米的长方形,“1 米”作单位的量值长3、宽2,对应的面积单位“1 平方米”的量值也是长3、宽2,总量值“3×2=6”。所以结果是6 个“1 平方米”。
所以,“所有的计算都是对度量单位个数的累加和细分”的说法是正确的。
