基于稀疏过零点信息的抗幅值失真时延估计方法

唐 俊，汪 照，白宇田

基于稀疏过零点信息的抗幅值失真时延估计方法

唐 俊1, 2，汪 照1, 2，白宇田1, 2

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学港口与海洋工程天津市重点实验室，天津 300350)

基于时延估计的TDOA方法广泛地应用于声学定位技术中，应用时引入的干扰会导致一定程度的幅值失真，从而影响时延估计的准确与稳定性．文中分析了不同干扰因素带来的影响，进而针对幅值失真问题，提出了一种新的基于信号过零点信息进行时延估计方法．该方法对需要进行时延估计的两路信号进行幅值归一化处理，得到仅含0、1两种特征值的稀疏化信号，在一定范围内将稀疏化信号错位相减得到误差系数函数，通过索引误差系数函数的最小值求得通道时延估计值．为了验证该方法的有效性，分别进行了数值模拟、耦合腔实验与室内混响定位实验，实验中采用广义互相关(GCC)时延估计方法作为对比，结果表明：对于模拟信号和耦合腔标准声源生成信号，该方法均有较好的抗干扰能力，在信噪比为-5dB时依然可以准确进行时延估计计算；与GCC方法相比，可用于极端条件如信号削波时的时延估计；在低采样率实验中，该方法较GCC方法受采样率降低影响小，在低采样率的条件下依然保留一定时延估计能力；在室内混响条件下的近距离声源定位实验中，该方法受声源距离、混响影响小，并且较GCC方法具备更强的抗突发干扰能力．文中所提出的方法能很好地抑制信号削波、低采样率、混响干扰等因素导致的幅值失真带来的影响，提升复杂环境下时延估计的精度与稳定性，面对突发干扰也表现出了更好的抗干扰能力．同时该方法设计简单、计算量较小，可满足对数据实时处理的需求．

时延估计；声学定位；幅值失真；过零点信息；室内混响

近年来，随着声学理论与传感器技术的快速发展，基于传感器的声源定位技术作为声学的重要研究方向，在军事、工业等领域中的应用日益增加．声源定位技术是使用传声器采集声源信号，进而对采集到的信号进行分析和处理，最终确定信号源位置的一种技术[1]．根据定位原理的不同，声源定位方法主要分为3类：①高分辨率谱估计方法[2]；②基于最大输出功率的可控波束成形算法[3]；③基于到达时间差(time delay of arrival，TDOA)的定位方法．其中基于TDOA的声源定位算法布置简单，计算量小，定位精度高，是一种应用范围最为广泛的定位方法[4-5]．

TDOA是一种通过估计信号到达不同监测单元的时间差，实现对信号源进行定位的方法[6]，主要由两个部分组成：第1部分是时延估计，也就是不同监测单元时间差的获取；第2部分是利用得到的时间差，结合数学方法得到声程差，由于监测单元的结构与位置是已知的，便可得到信号源的具体位置[7]．其中时延估计是关键部分[8]，会直接影响到声源定位的结果，干扰误差的产生往往也出现在时延估计部分．

为了减小时延估计误差，提升时延估计的准确性与稳定性，历年来国内外学者从多个角度进行了研究，针对不同问题提出了一系列方法，如采用广义互相关法、最小均方自适应(LMS)算法[9]、基于空间的特征值分解(EVD)方法[10]、高阶统计量法[11]以及基于传递函数比(ATF-s ratio)的方法等[12]．这些研究可以在一定程度上提升时延估计精度，但大多受信号幅值信息影响较大，对于一些复杂如幅值失真情况下，实现准确、稳定的时延估计还需要进一步研究．

自从二战期间，Vlech等[13]完成了一项关于信号削波对相关性影响的开创性工作，提出反正弦定律(arcsine law)以来，人们对量化对信号相关性的影响进行了大量研究[14-15]，发现幅值信息丢失，即幅值失真会一定程度影响时延估计的结果．导致幅值失真的因素有很多，如混入干扰信号或采样频率相对过低等情况，以及极端的信号幅值超过传感器量程，采样点离信号源过近，导致信号幅值信息存在大量错误或丢失等情况[16]．这些情况往往不易规避，受其影响，传统的时延估计方法会难以达到理想效果甚至不再适用．

针对以上问题，文中分析了时延估计误差产生的主要原因，提出了一种基于稀疏过零点信息的时延估计方法，该方法不依赖信号的幅值信息特征，在信号幅值严重失真的情况下，依然能得到较为准确进行时延估计．与传统的时延估计方法相比，具有更强的抗干扰能力．

1 时延估计误差分析

1.1 互相关时延估计

广义互相关(generalized cross-correlation，GCC)算法是目前应用最广的时延估计，算法原理如图1 所示[18]．

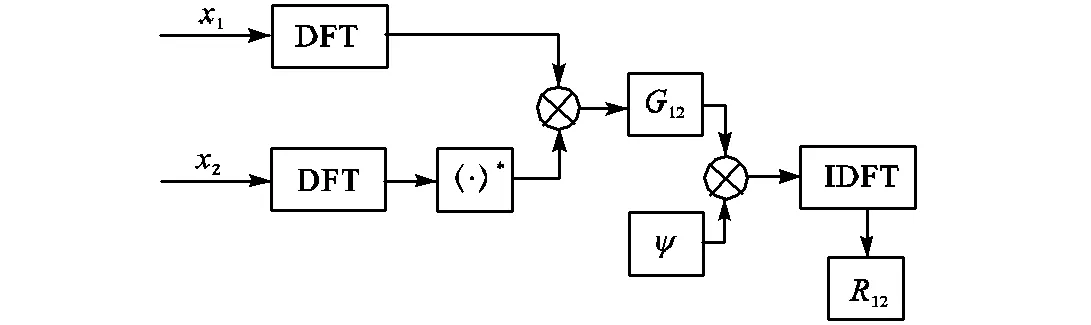
图1 GCC算法原理

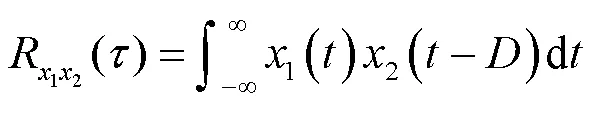
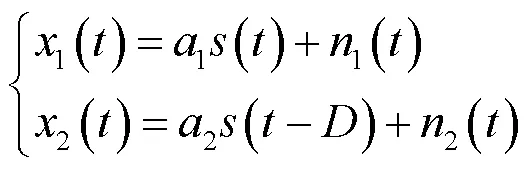
将式(2)代入式(1)得

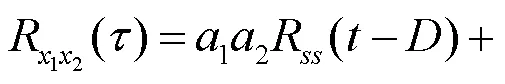
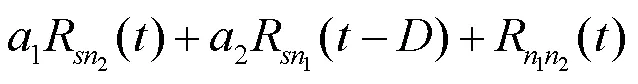
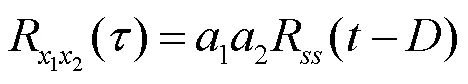
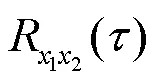
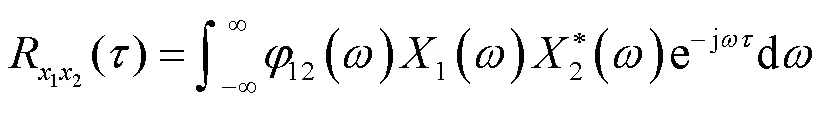
加权函数的选取与应用场景有关，往往需要对噪声信号特征进行统计．本文选用加权函数为1的基本互相关作为对照组，以下简称为互相关．

在根据声信号、振动信号、电磁波信号等物理信号进行时延估计时，有多种因素导致信号的幅值失真，如：采集时混入干扰信号，在采集过程中会存在次级干扰声源或室内混响等；面对高频信号时采样频率的限制[20]，如无线传感器在使用过程中因带宽较低，很难以高采样率进行实时采集；传感器精度、量程有限以及声场衰变的不一致性[21]等因素．

其中导致幅值误差的最主要因素是在信号采集过程混入的干扰信号以及数据采集设备的采样频率限制．

1.2 幅值失真下的时延估计分析

1.2.1 干扰噪声影响

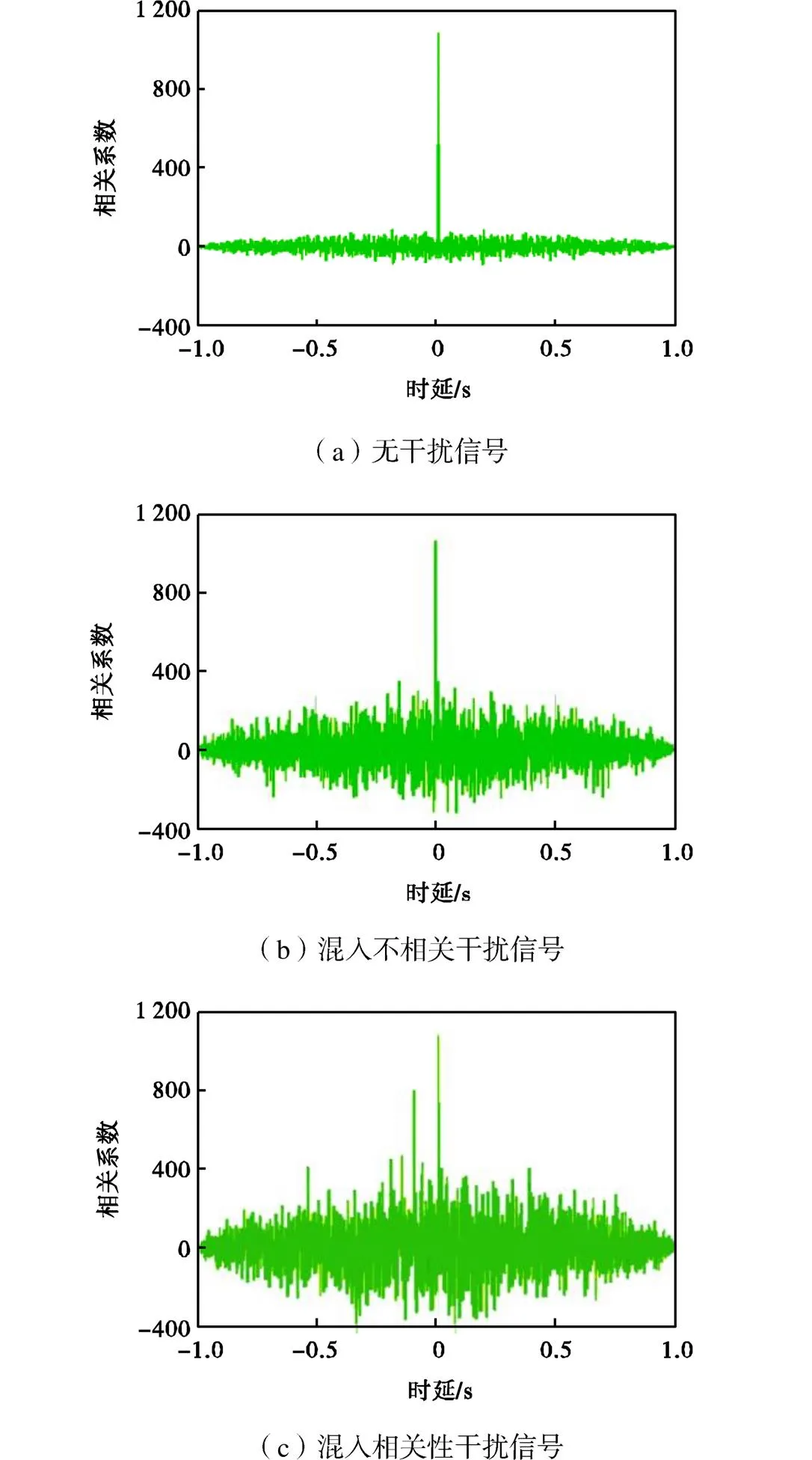
图2 不同干扰下的时延估计结果

1.2.2 采样频率限制

实验过程中，受数据采集仪器本身的限制，系统采集到的信号是有限的离散点，而实际信号是一条连续的线，因此只有保证点的数量足够多，且采样的初始相位均为整数，才可得到有效的信号波形．

设备使用过程中，采样初始相位难以保证，因此必须依靠较高的采样频率来保证采样波形的正确性．但是对于混有高频信号的波形，往往会出现传感器的采样频率到达瓶颈的情况．一旦采样率不够，就会导致采集到的波形丢失大量幅值信息，给时延估计结果带来较大影响．对于某一波形，分别采用1000、3000、10000Hz的采样频率进行采样，得到的信号时域曲线如图3(a)所示．可以看出采样率不同对信号幅值信息会产生巨大的影响．为进一步分析采样率限制对信号幅值信息的影响，在信号时域曲线中随机选取片段进行局部放大，如图3(b)所示．

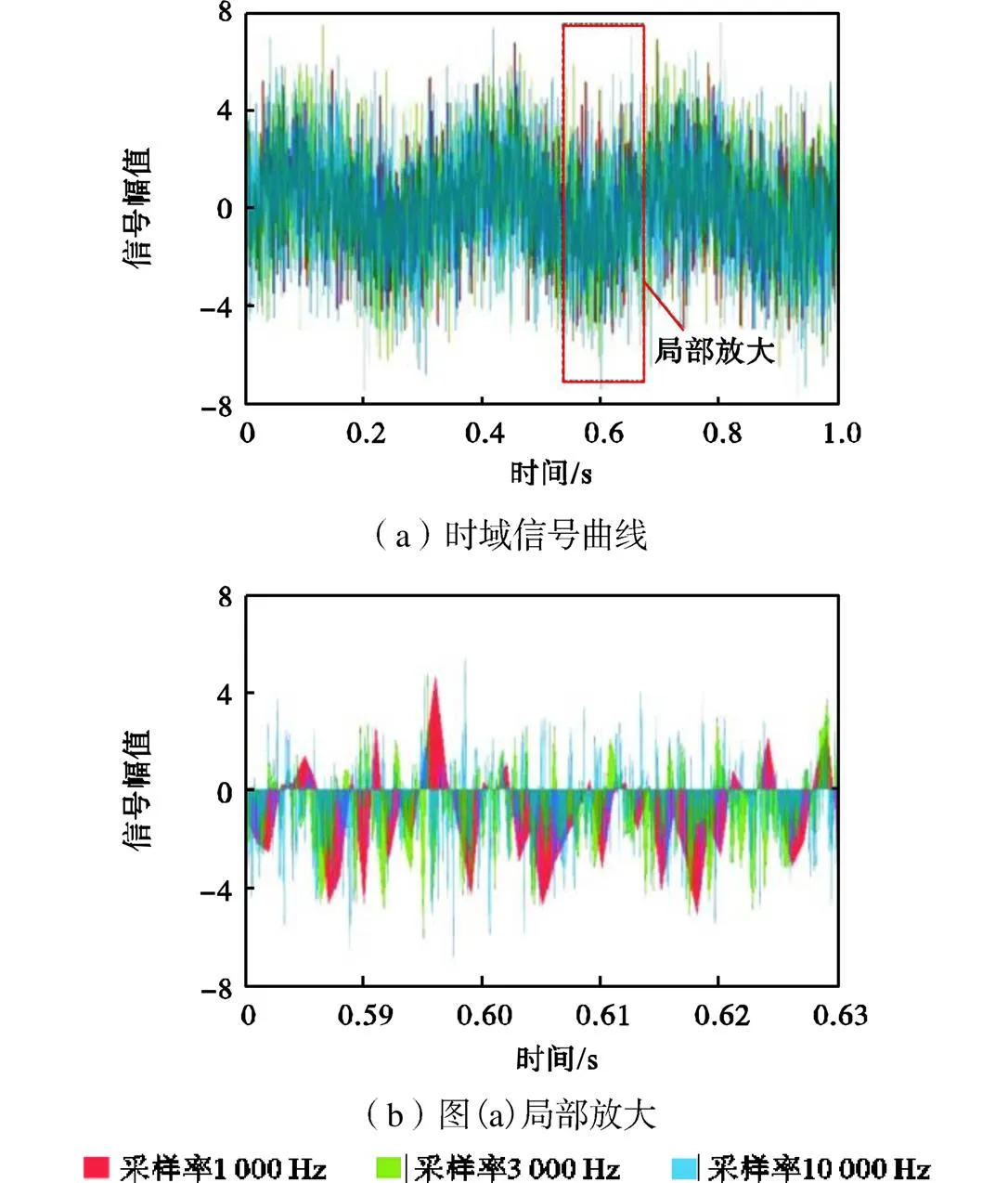
图3 不同采样频率下的波形

从图3(b)中可以发现，即使是同一信号，采用不同的采样频率，会得到差异较大的波形曲线，即不同采样频率所保留的波形幅值信息不同，系统采样频率越高，获得的信号波形幅值信息越完整．除了以上介绍的两种主要幅值误差因素以外，还有一些次要因素同样会造成幅值失真，给时延估计带来影响．为了减小或避免幅值失真的影响，提高时延估计准确度，文中提出了一种基于稀疏过零点信息的时延估计方法，该方法可以最大限度地降低对信号幅值信息的依赖度，在信号幅值信息失真情况下依然能准确获取时延估计值．

2 过零点信息算法

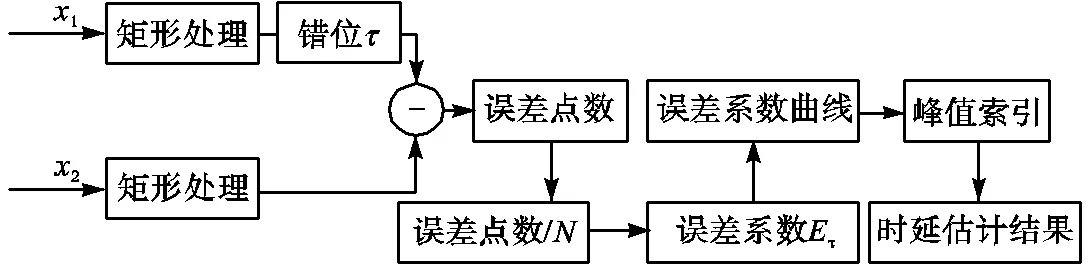
图4 过零点信息算法原理

对于如图4所示的时延估计系统有

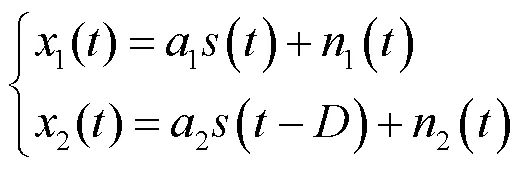
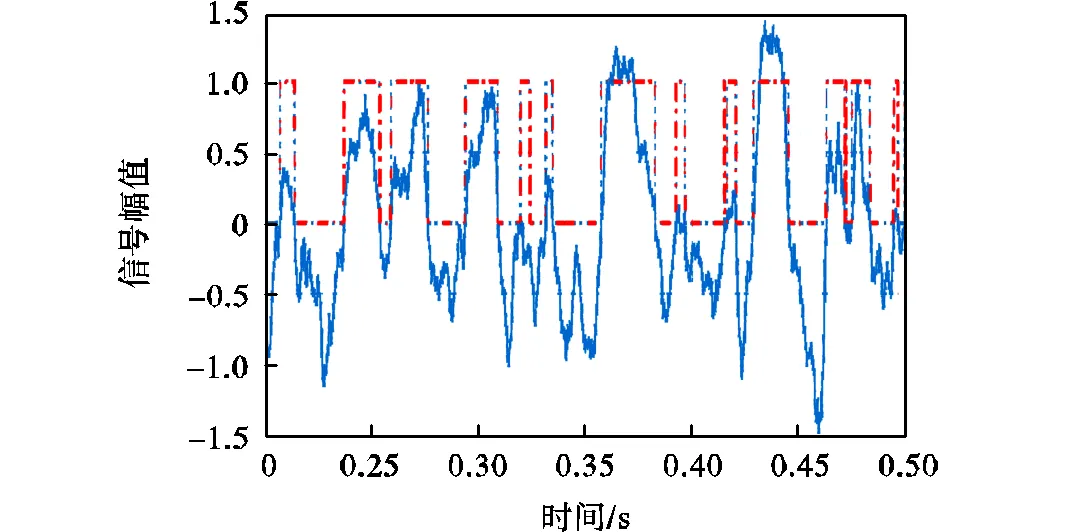
图5 信号波形幅值信息稀疏化处理

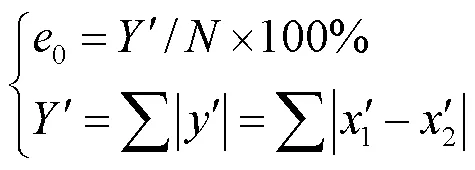
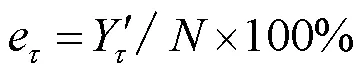
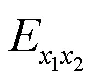
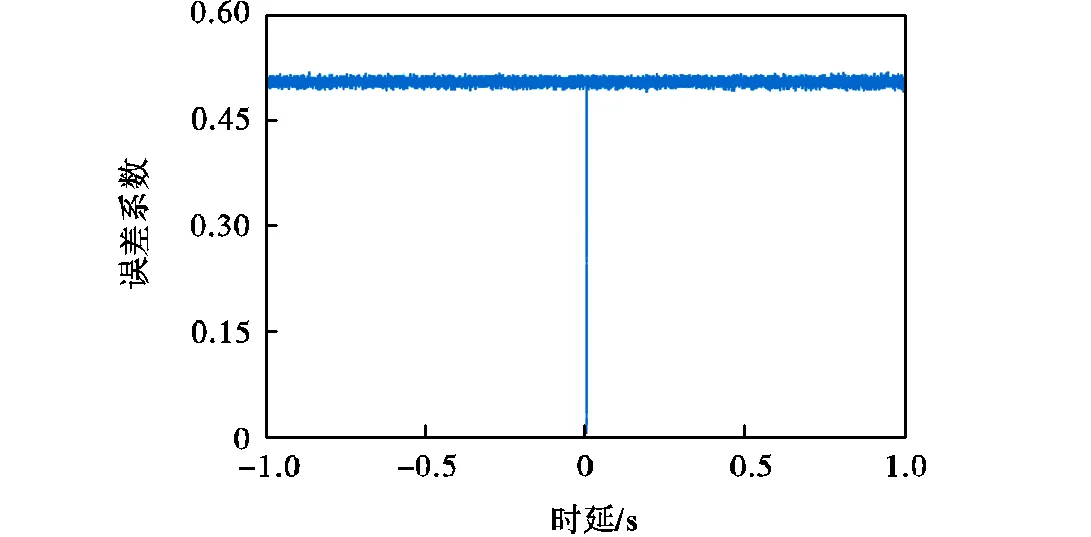
图6 理想情况下的误差系数曲线

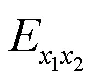
与传统方法相比，基于信号过零点信息的时延估计方法不仅适用于一般条件下的时延估计计算，也可满足信号失真条件下的时延估计需求：通过矩形处理，可以将信号转换为0、1构成的序列，发生小幅度信号失真时，信号曲线上绝大部分点的幅值正负信息不会发生改变，因此对0、1序列几乎不会造成扰动；当信号发生较大幅度失真时，如引入强突发干扰，此时由于归一化的处理方式，大的幅值变化会转换为有限的0、1序列变化，从而有效地限制强干扰对曲线整体的影响，获得更加精确、稳定的时延估计结果．

3 数值模拟

为验证过零点信息的时延估计算法的有效性，设计了数值模拟实验，并在同一种条件下，将其与互相关时延估计算法进行对比．

高斯随机信号是概率密度分布为正态分布的随机信号，是一种常见的随机信号[23]．模拟实验中，选用两路标准差为0.2的高斯随机信号作为源信号，设置两路信号的通道时延0.5s，采样率为10000Hz；在两路高斯信号中均混入不相关白噪声作为干扰信号，调节白噪声大小使信噪比SNR分别为5、0、-5dB进行测试，时延估计结果如图7和图8所示．

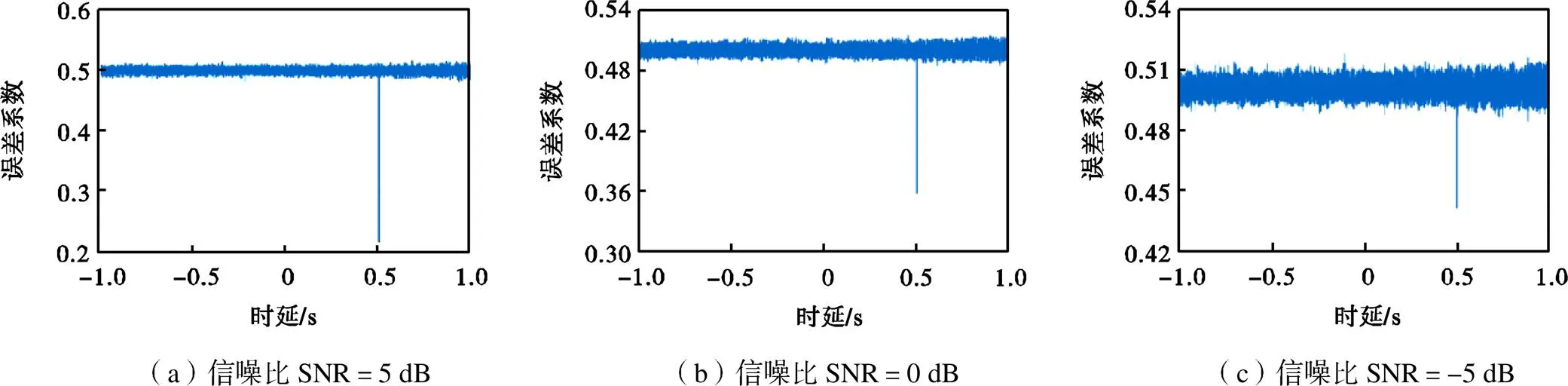
图7 过零点信息算法在不同信噪比条件下的时延估计

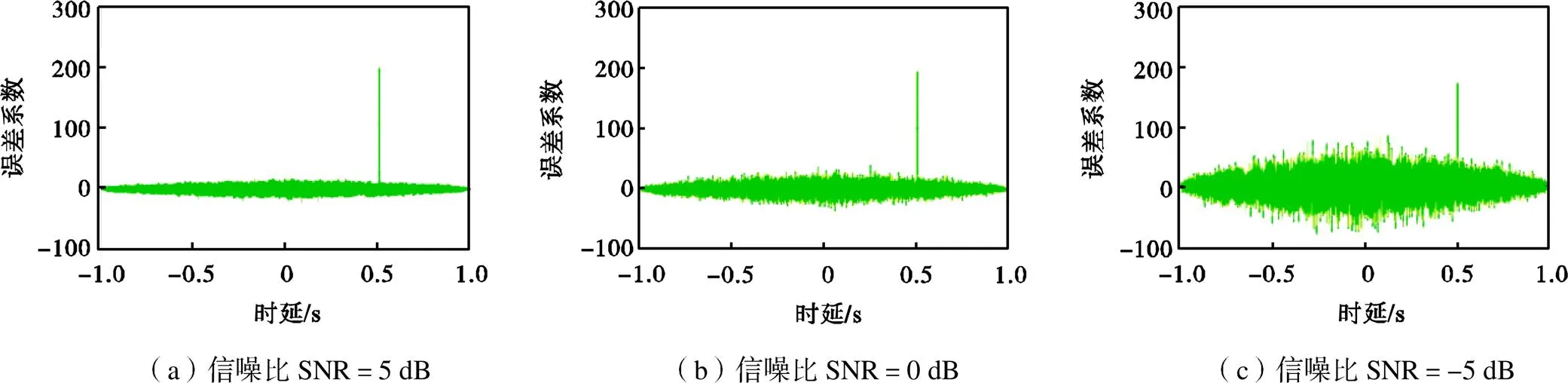
图8 互相关算法在不同信噪比条件下的时延估计

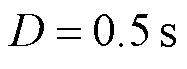
为进一步验证该方法在极端条件下的时延估能力，选用两路标准差为1.0的高斯随机信号，设置通道时延为0.5s，采样率为10000Hz；在其中混入不相关白噪声作为干扰信号，使信噪比为-5dB；对两路信号进行削波处理，设置1.0、-1.0为信号幅值上、下限，用来模拟信号幅值严重失真的极端工况，如图9所示．

这种幅值失真的情况通常在传感器与信号源距离过近或信号幅值超传感器量程时出现．以图9所示的削波信号为对象，分别使用过零点信息的时延估计算法和互相关时延估计算法进行时延估计，结果如图10所示．

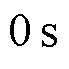
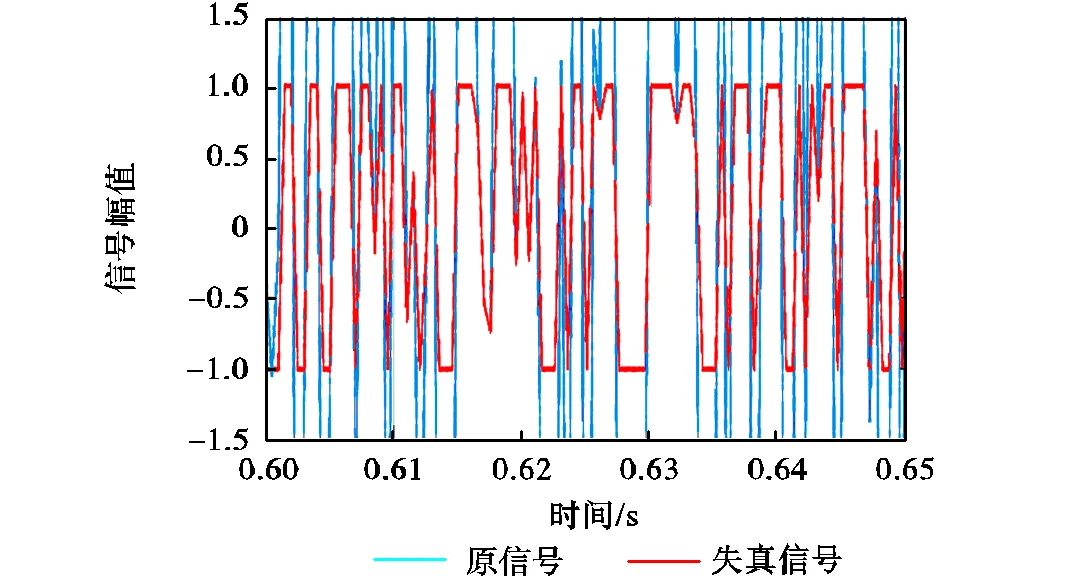
图9 原信号与幅值失真的信号

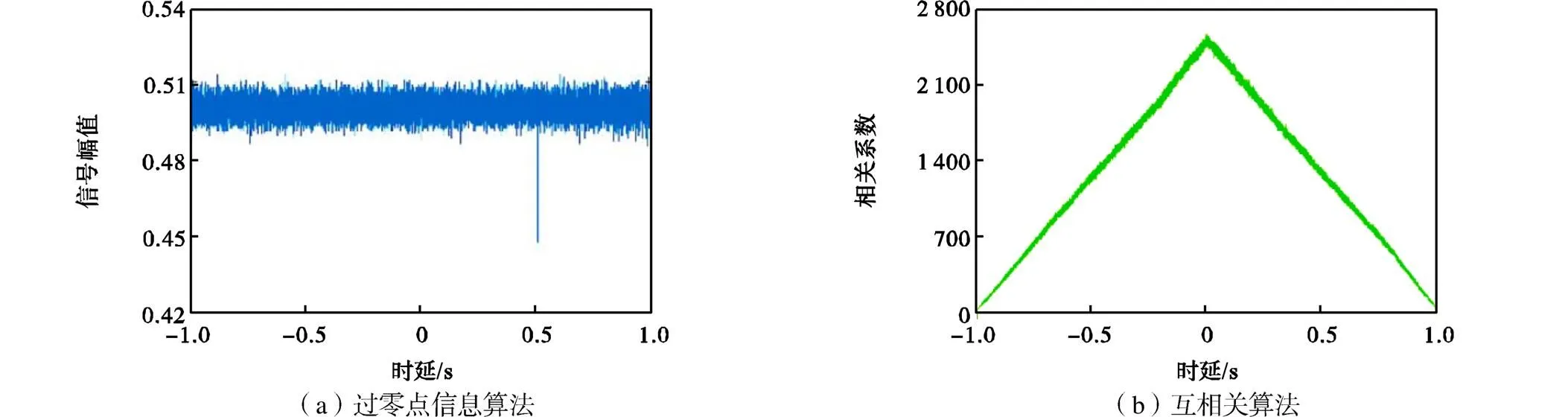
图10 信号幅值失真情况下的时延估计

4 时延估计实验与分析

4.1 基于耦合腔标准声信号的时延估计

基于耦合腔标准声源设计了时延估计实验，进行了该方法在实际应用中的可靠性研究：将两个130E22型标准麦克风传声器分别插入到两个AWA14424S型耦合腔标准声源中，基于两个麦克风传声器采集的声信号进行时延计算．实验使用耦合腔标准声源发声可以避免环境干扰，并可以有效控制信号的信噪比．

实验中，输入到两路耦合腔标准声源的信号为标准差为0.2高斯随机信号，两路信号的时延值设置为0.5s，采样率为10000Hz；两路信号均混入不相关白噪声，使信噪比分别为5、0、-5dB，分别使用过零点信息的时延估计算法和互相关时延估计算法对麦克风传声器信号进行时延估计，实验结果如图11和图12所示．

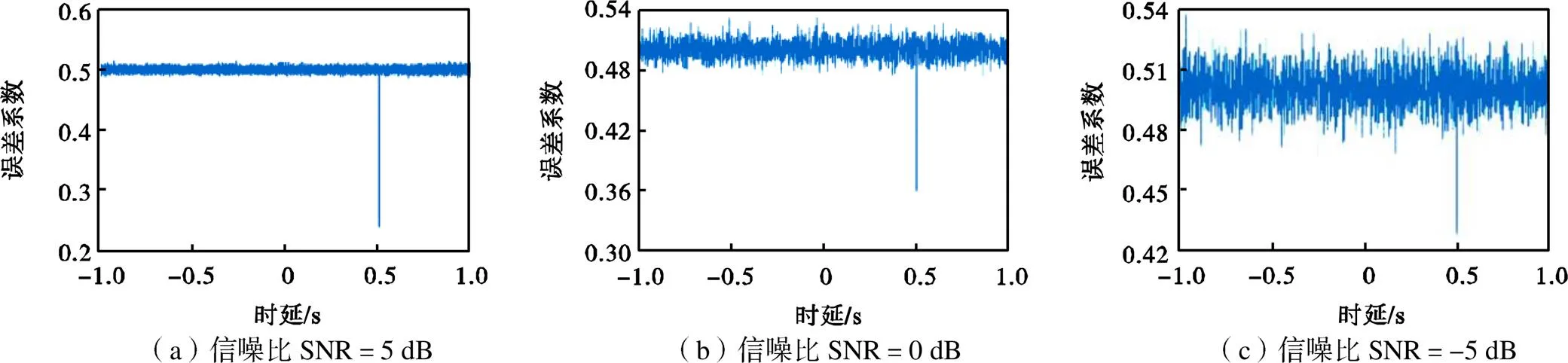
图11 过零点信息算法在不同信噪比条件下的耦合腔声源实验

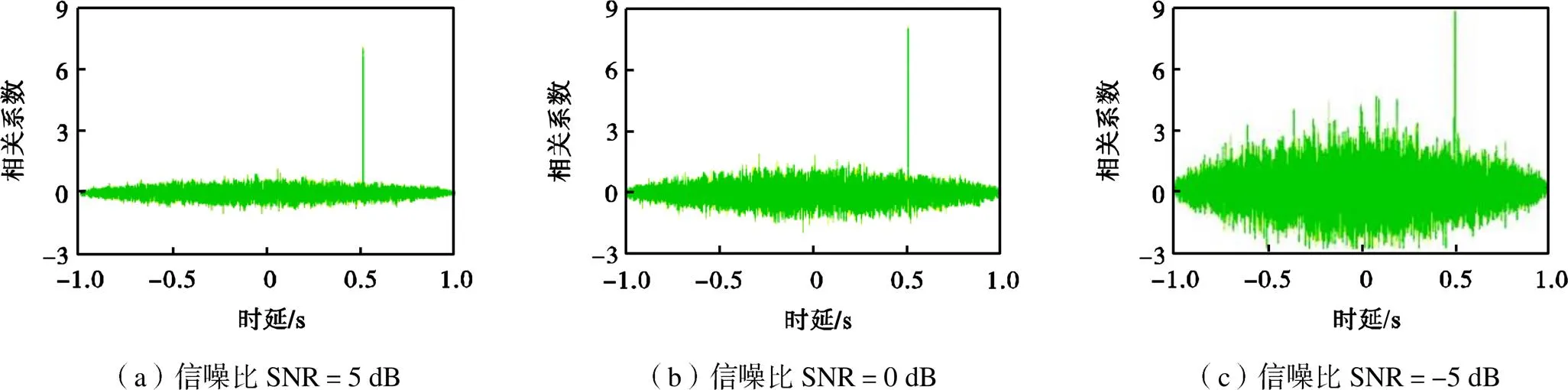
图12 互相关算法在不同信噪比条件下的耦合腔声源实验

为进一步研究采样频率对两种方法的影响，设计了不同采样频率下的时延估计实验．在信噪比为  -5dB，源信号时延为0.5s时，在1000、3000、10000Hz采样频率下，分别使用过零点信息算法与互相关算法对信号进行时延估计，其结果如图13和图14所示．

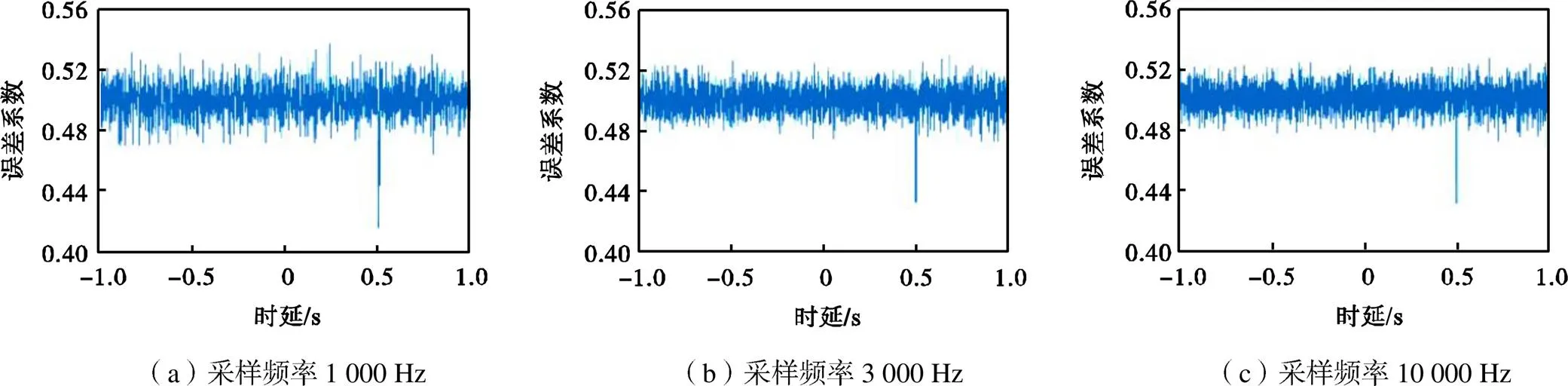
图13 过零点信息算法在不同采样频率下的时延估计

图14 互相关算法在不同采样频率下的时延估计

由图13可以发现，过零点信息算法对采样频率的变化并不敏感，与互相关算法相比，即使在低采样频率下依然可以计算出准确的时延值．这是由于在低的采样频率下，信号过零点信息总是比信号幅值信息更容易保留，因此过零点信息算法依然可以表现出较好的时延估计特性．

从图14中可以发现，互相关算法受采样频率影响较为明显：随着采样频率的增加，信号信息更加精确，得到的时延估计结果也更准确；而在较低的采样频率下，互相关算法难以得到理想的时延估计结果．

4.2 混响室内时延估计实验

传感器离信号源过近时，采集到的信号易失真，同时在混响室内，由于存在大量反射，会进一步使信号幅值失真．这种条件下，传统的互相关时延估计方法往往很难进行准确的时延估计[24]，为验证过零点信息的时延估计方法在极端工况下的时延估计准确性，在混响室内进行了混响条件下的时延估计实验．

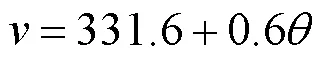
得到声速，进而得到定位距离．

为了对该方法受突发干扰时的稳定性进行研究，在实验过程中引入如图16所示的具有持续短、幅值大特征的突发干扰信号．

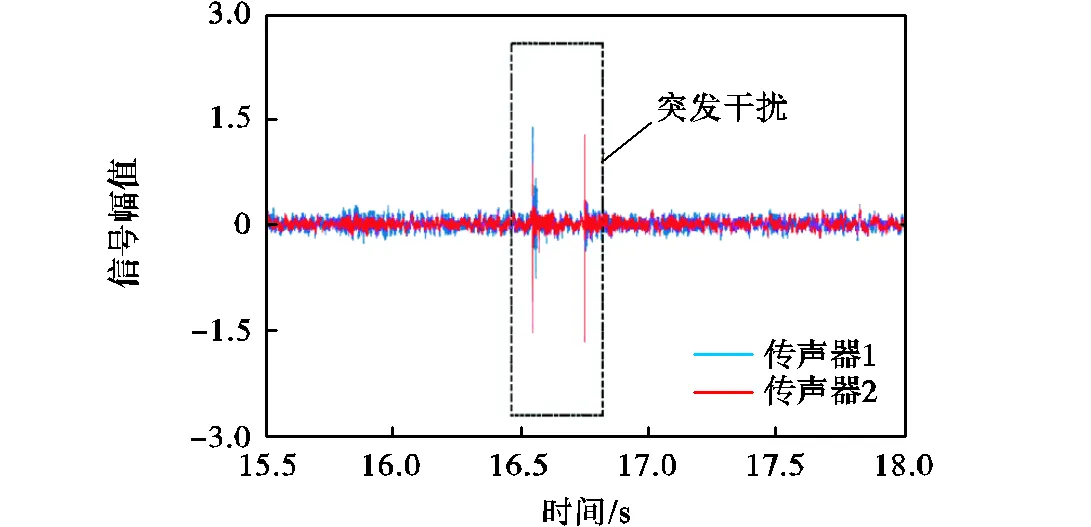
图16 信号特征

分别采用过零点信息时延估计算法和互相关时延估计算法，在混响条件下对传声器1和传声器2采集到的声信号进行时延估计，确定传声器间距．对两个传声器间距的定位结果如图17所示．

从结果中可以发现，对于室内混响复杂声场的近距离声源定位，由于信号幅值失真严重，采用互相关方法获取精确的时延估计值已经变得十分困难，所得到的定位结果在1.2m上下浮动；而基于信号过零点信息的时延估计方法受幅值失真影响小，定位结果与实际距离十分接近，表现出更加稳定、精确的特性．

当实验中引入突发性干扰时，两种方法都表现出了一定的偏离，而互相关方法的偏离较大，这是由相关系数的计算原理所引起的：相关系数的大小与幅值呈一种类正比关系，因此具有大幅值的突发性干扰会导致互相关算法的时延估计结果向其产生较大偏离；而对于过零点信息算法，由于其计算机理不同，大的幅值变化在归一化处理环节被转换为有限的0、1序列变化，因此降低了对时延估计的扰乱，在结果上表现为较小的偏离．

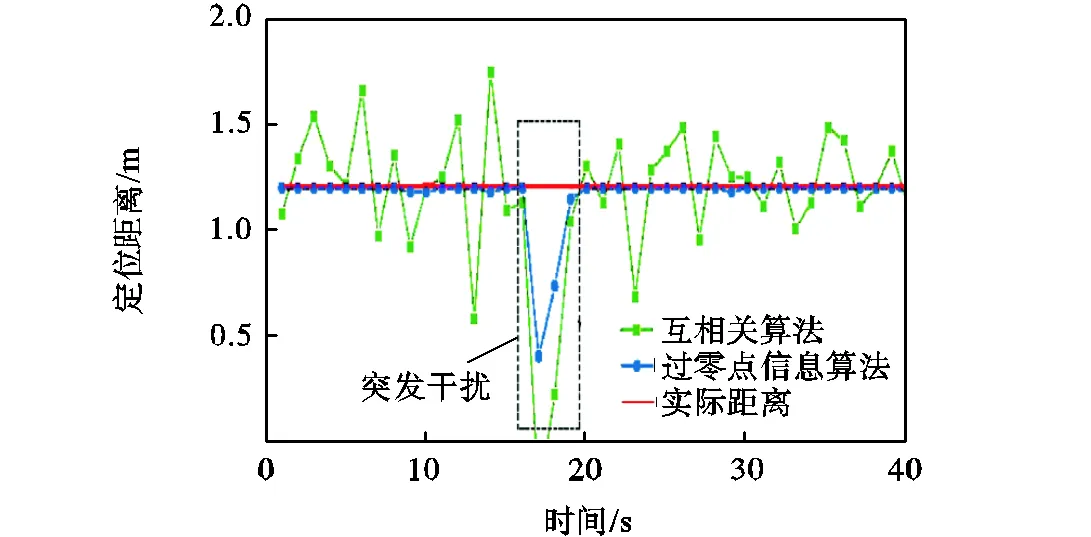
图17 定位结果

5 结 语

文中基于传统时延估计方法易受信号幅值失真影响的问题，分析了误差的主要来源，并提出了一种基于稀疏过零点信息的时延估计方法．该方法通过对两路信号幅值进行归一化处理，绘制误差曲线并最终得到时延值，有效避免了幅值信息失真带来的影响.

根据使用环境的不同，分别设计了不同条件下数值模拟与具体实验，验证了方法的可靠性，实验结果表明：该方法易于设计，实现简单，对各类使用条件都有着较好的时延估计效果，适用范围较为广泛；可以有效克服信号幅值失真的影响，在较为极端如削波、混响条件下依然可以保证不错的效果，鲁棒性较好；对采样频率的变化不敏感，可用于低采样频率下的时延估计实验；对于突发干扰，由于计算原理特殊，受影响较小，稳定性较强．

另外，文中所提方法采用了一种新的时延估计思路，进一步研究范围广泛．例如可设计一种低成本、低功耗的仅需测量信号幅值正负的传感器，用来拓展声源定位的应用场景，可以预见在未来有着广阔的发展空间．

［1］ Kundu T. Acoustic source localization[J]. Ultrasonics，2014，54(1)：25-38.

［2］ Gierlich R. Joint estimation of spatial and motional radar target parameters by multidimensional spectral analysis[C]// Proceedings International Radar Symposium. Dresden，Germany，2015：95-101.

［3］ Shi W，Li Y，Zhao L，et al. Controllable sparse antenna array for adaptive beamforming[J]. IEEE Access，2019，7：6412-6423.

［4］ 李保伟，张兴敢. 基于广义互相关改进的麦克风阵列声源定位方法[J]. 南京大学学报(自然科学)，2020，56(6)：917-922.

Li Baowei，Zhang Xinggan. Improved microphone array sound source localization method based on generalized mutual correlation[J]. Journal of Nanjing University(Natural Science)，2020，56(6)：917-922(in Chinese).

［5］ Huang Y T，Benesty J，Elko G W. Passive acoustic source localization for video camera steering[C]// Proceedings of IEEE International Conference on Acoustic，Speech and Signal Processing. Istanbul，Turkey，2000：909-912.

［6］ Nesta F，Omologo M. Generalized state coherence transform for multidimensional TDOA estimation of multiple sources[J]. IEEE Transactions on Audio，Speech and Language Processing，2012，20(1)：246-260.

［7］ 张焕强，黄时春，蒋伟康. 基于传声器阵列的汽车鸣笛声定位算法及实现[J]. 噪声与振动控制，2018，38(3)：10-14.

Zhang Huanqiang，Huang Shichun，Jiang Weikang. Algorithm and implementation of car horn sound localization based on microphone array[J]. Noise and Vibration Control，2018，38(3)：10-14 (in Chinese).

［8］ 王华松，赵 鑫. 基于端点检测的精确时延提取方法及其定位精度分析[J/OL].声学技术，https://kns.cnki. net/kcms/detail/31.1449.TB.20200908.0923.002.html，2020-12-04.

Wang Huasong，Zhao Xin. Analysis of accurate time delay extraction method based on endpoint detection and its localization accuracy[J/OL]. Acoustic Technology，https://kns.cnki.net/kcms/detail/31.1449.TB.20200908.0923.002.html，2020-12-04(in Chinese).

［9］ Youn D，AhmedN，Carter G. On using the LMS algorithm for time delay estimation[J]. IEEE Transactions on Acoustics，Speech and Signal Processing，1982，30(5)：798-801.

［10］ Benesty J. Adaptive eigenvalue decomposition algorithm for passive acoustic source localization[J]. Journal of the Acoustical Society of America，2000，107(1)：384-391.

［11］ 雷正伟，刘 福，华 翔. 小波高阶统计量的时延估计及在超声应力检测中的应用[J]. 计算机测量与控制，2008(11)：1550-1552.

Lei Zhengwei，Liu Fu，Hua Xiang. Time delay estimation of wavelet higher order statistics and its application in ultrasonic stress detection[J]. Computer Measurement and Control，2008(11)：1550-1552 (in Chinese).

［12］ Dorfan Y，Plinge A，Hazan G. Distributed expectation-maximization algorithm for speaker localization in reverberant environments[J]. IEEE/ACM Transactions on Audio，Speech and Language Processing，2018，26(3)：682-695.

［13］ Vleck J H V，Middleton D. The spectrum of clipped noise[J]. Proceedings of the IEEE，1966，54(1)：2-19.

［14］ Watts D G. Ageneral theory of amplitude quantization with applications to correlation determination[J]. Proceedings of the IEE，Part C：Monographs，1962，109(15)：209-218.

［15］ Cooper B F C. Correlators with two-bit quantization[J]. Australian Journal of Physics，1970，23：521-528.

［16］ Brennan M J，Gao Y，Ayala P C. Amplitude distortion of measured leak noise signals caused by instrumentation：Effects on leak detection in water pipes using the cross-correlation method[J]. Journal of Sound and Vibration，2019，461：114905.

［17］ Knapp C H. The generalized correlation method for estimation of time delay[J]. IEEE Transactions on Acoustics，Speech and Signal Processing，1976，24(4)：320-327.

［18］ Kothandaraman M，Law Z，Gnanamuthu E M A， et al. An adaptive ICA based cross-correlation techniques for water pipeline leakage localization utilizing acousto-optic sensors[J]. IEEE Sensors Journal，2020，20(17)：10021-10031.

［19］ 周鹤峰，田章福. 基于广义互相关算法的时延估计改进[C]// 2020中国西部声学学术交流会论文集. 酒泉，中国，2020：450-452.

Zhou Hefeng，Tian Zhangfu. Improvement of time delay estimation based on generalized mutual correlation algorithm[C]// Proceedings of the 2020 Western China Acoustical Academic Exchange Conference. Editorial Board of Acoustics Technology. Jiuquan，China，2020：450-452 (in Chinese).

［20］ 茅惠达，张玲华. 声源定位中广义互相关时延估计算法的研究[J]. 计算机工程与应用，2016，52(22)：138-142.

Mao Huida，Zhang Linghua. Research on generalized mutual correlation time delay estimation algorithm in acoustic source localization[J]. Computer Engineering and Applications，2016，52(22)：138-142 (in Chinese).

［21］ 浦宏杰，邱小军，王季卿. 耦合空间中不同衰变类型声场的边界研究[J]. 声学学报，2009，34(6)：533-538.

Pu Hongjie，Qiu Xiaojun，Wang Jiqing. Acoustic field boundaries of coupled volumes with different energy decay styles[J]. Acta Acustica，2009，34(6)：533-538(in Chinese).

［22］ 吴晓平，祁亨年. 未知信号传播速度的TDOA测量远近场统一定位方法[J]. 传感技术学报，2020，33(7)：1049-1055.

Wu Xiaoping，Qi Hengnian. Unified far and near field localization for TDOA measurements under unknownsignal propagation speed[J]. Chinese Journal of Sensors and Actuators，2020，33(7)：1049-1055(in Chinese).

［23］ Lopes P A C. Bayesian step least mean squares algorithm for Gaussian signals[J]. IET Signal Processing，2020，14(8)：506-512. .

［24］ 胡章芳，乐聪聪，张 毅，等. 混响环境下基于分频的广义互相关时延估计算法[J]. 计算机工程，2018，44(9)：269-273.

Hu Zhangfang，Le Congcong，Zhang Yi，et al. Generalizedcross-correlation time delay estimation algorithm based on frequency division in reverberation environment[J]. Computer Engineering，2018，44(9)：269-273(in Chinese).

［25］ 杜功焕，朱哲民，龚秀芬. 声学基础[M]. 3版. 南京：南京大学出版社，2012.

Du Gonghuan，Zhu Zhemin，Gong Xiufen. Fundamentals of Acoustics[M]. 3rd ed. Nanjing：Nanjing University Press，2012(in Chinese).

Anti-Amplitude Distortion Time Delay Estimation Method Based on Sparse Cross-Zero Information

Tang Jun1, 2，Wang Zhao1, 2，Bai Yutian1, 2

(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. Tianjin Key Laboratory of Port and Ocean Engineering of Tianjin University，Tianjin 300350，China)

The time delay of arrival (TDOA) method based on time delay estimation is widely used in acoustic localization techniques. The interference introduced during its application can lead to a certain degree of amplitude distortion，which affects the accuracy and stability of time delay estimation. In this paper，the effects of different interference factors are analyzed，and a new method of time delay estimation based on signal cross zero information is proposed for the amplitude distortion problem. The method normalizes the amplitude of the two signals for delay estimation to obtain a sparse signal containing only two eigenvalues：0 and 1. The error coefficient function is obtained by subtracting the sparse signal from the misalignment within a certain range，and the channel delay estimation is obtained by indexing the minimum value of the error coefficient function. To verify the effectiveness of the method，numerical simulations，coupled-cavity experiments，and indoor reverberation localization experiments were carried out. The results were compared using the generalized cross-correlation (GCC) time delay estimation method. The results show that the proposed method has good immunity to interference for both analog and coupled-cavity standard source-generated signals. Moreover，the method can give accurate time delay estimation at a signal-to-noise ratio of  -5dB. Compared with the GCC method，the proposed method can be used for delay estimation under extreme conditions such as signal clipping. In low sampling rate experiments，the method is less affected by the reduced sampling rate than the GCC method，and it retains some delay estimation capability under low sampling rate conditions. In indoor reverberation experiments，the method is less affected by the source distance and reverberation and shows stronger resistance to sudden interference than the GCC method. The proposed method can suppress the effects of amplitude distortion caused by signal clipping，low sampling rate，and reverberation interference. Moreover，the proposed method results in improved accuracy and the stability of time delay estimation in complex environments and better immunity to sudden interferences. Additionally，the proposed method is simple in design，small in computation，and can meet the demand for real-time data processing.

time delay estimation；acoustic localisation；amplitude distortion；cross-zero information；indoor reverberation

10.11784/tdxbz202012045

TB533

A

0493-2137(2022)02-0211-10

2020-12-20；

2021-03-26.

唐 俊（1979—  ），男，博士，副研究员．Email：m_bigm@tju.edu.cn

唐 俊，tangjun@tju.edu.cn.

装备预先研究资助项目(公开)(61402100104)；国家自然科学基金资助项目(11204010)；天津大学自主创新基金资助项目(2018XZY-0019).

the Equipment Advance Research Project (Open)(No.61402100104)，the National Natural Science Foundation of China (No.11204010)，Tianjin University Independent Innovation Fund(No. 2018XZY-0019).

(责任编辑：孙立华)