一种基于麦克风阵列用于分离单极子和偶极子声源的方法
2022-03-29周纬杨明绥马威
周纬,杨明绥,马威
1.上海交通大学 机械与动力工程学院,上海 200240
2.中国航空发动机集团有限公司 沈阳发动机研究所,沈阳 110015
3.上海交通大学 航空航天学院,上海 200240
4.上海交通大学 燃气轮机与民用航空发动机教育部工程研究中心,上海 200240
随着社会的快速发展,噪声对人类生活、工业生产造成的弊端日益受到重视,如何更好地识别潜在的噪声源位置及其强度,对于降噪设计尤为重要。基于延迟叠加的波束成形算法CB(Conventional Beamforming),具有简便、计算速度快和鲁棒性高的优点,被广泛应用于噪声源的位置和强度估计。但是在实际工程应用中,噪声源可能同时包含单极子源和偶极子源,应用单极子传播假设的波束成形算法求解时,无法准确进行声源定位。目前学术界还没有有效的声源定位技术,可以分离单极子源和偶极子源。
为了有效地对组合声源进行分离,可以从反卷积算法和声源传播模型入手。由于受到阵列孔径的限制,波束成形算法在低频情况下的空间分辨率较低。因此,具有高分辨率的反卷积算法,如DAMAS (Deconvolution Approach for the Mapping of Acoustic Sources)算法、CLEAN算法,及其拓展算法DAMAS-C算法、CLEANSC(CLEAN for Spatial Source Coherence)算法应运而生。在航空声学应用中,美国国家航空航天局(NASA)的Langley喷流噪声实验室成功运用DAMAS算法对几种不同构型的喷嘴喷流噪声进行了测量,比其他反卷积算法取得了更好的效果,此后DAMAS算法被广泛地运用于航空声学研究。由于DAMAS 具有迭代计算量大、计算成本高的缺点,Ma和Liu通过压缩网格提高了DAMAS算法的计算效率。
另一方面,波束成形算法是通过建立声源传播模型,根据声源辐射在空间传播函数推导出声源位置,所以要求定位声源模型与所建立的求解模型要对应,而构建声源模型往往受声源类型、运动状态影响。通常导向矢量采用的是基于单极子传播特性的假设,因此采用标准波束成形技术无法准确估计一个简单偶极子的位置和强度,Jordan等发现了这个问题,并对信号处理过程进行修正以考虑偶极子的传播特性。为了修正偶极子假设模型,Liu等进一步推导了偶极子的声源辐射传播模型,提出了一种新的偶极子波束成形,改进了以前的信号校正方法,并利用实验和仿真验证了该方法恢复偶极子源的能力。此外,如果声源处在运动中,由于存在多普勒效应,用于静止声源定位的反卷积算法无法有效识别运动声源,因此产生了运动波束成形算法。
在实际应用中,声源可能由不同类型、不同运动状态的子声源组成,因此学术界寻求可以分离组合声源的成像算法。为了处理由静止声源和运动声源组成的组合声源,Mo 和Jiang基于DAMAS算法,在波束成形输出和实际声源分布之间构造一个线性方程组,成功将一个静止源与一个运动声源分离开来。当声源数目较多时,Schmidt和Franks在传统波束成形的基础上,将导向矢量用导向矩阵表示,矩阵的每列对应不同模型假设的声源。在涉及声源相干性的问题时,Yardibi等提出一种用于相干声源定位的协方差拟合方法,可以有效计算复杂度较低的非相干、部分相干乃至相干声源。Suzuki进一步设计了一种广义逆波束成形算法,通过将交叉互谱矩阵分解成特征模提取每个相干信号,利用广义逆技术给出每个声源的参考解。受Suzuki启发,Pan等也是利用交叉谱矩阵分解,设计了一种多极子正交波成形算法,通过对特征向量的归一化消除了声源的指向性,用球面谐波表示声源,声源的类型和方向可以从重建的辐射模式中推导出来,可以更准确地估计声源的位置、类型和方向。
尽管学术界在识别多种声源上做出了很多努力,但是还没有比较有效的成像算法可以将组合声源分离开。受Mo和Jiang分离运动和静止声源的启发,本文提出一种混合反卷积算法Hybrid DAMAS(HD),用于分离包含单极子源和偶极子源的组合声源。所设计的混合反卷积算法建立在DAMAS算法上,并采用压缩网格法来优化计算效率。在实际声源分布与波束成形输出间构建一个线性方程组,通过求解线性方程组,同时从单极子波束成形和偶极子波束成形中提取单极子源和偶极子源。本文设计了4个数值仿真算例及2组实验来检验方法的有效性,考察定位位置误差和强度误差2个指标,并与波束成形算法和DAMAS算法作比较。
1 理论分析
1.1 声源模型
给定一个声源在具有稳定流动的均匀介质中位置ξ(1,2,…,),直角坐标系下的麦克风位置x (1,2,…,),马赫数列向量/,其中为流体流速。计算从声源到采集麦克风的传播矢量R=x -ξ,设置1、声源频率、声速。
计算单极子声源在流体中的传播时间Δ,以及在直角坐标系下的格林函数g
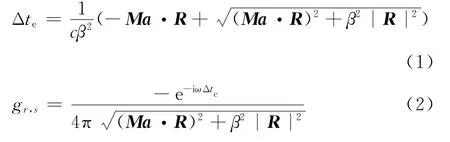
式中:为声源角频率。
一个偶极子声源可以认为是由2个相位相反的单极子声源组成,设置2个单极子源距离矢量,对于给定的,求解频域内偶极子近场波动方程
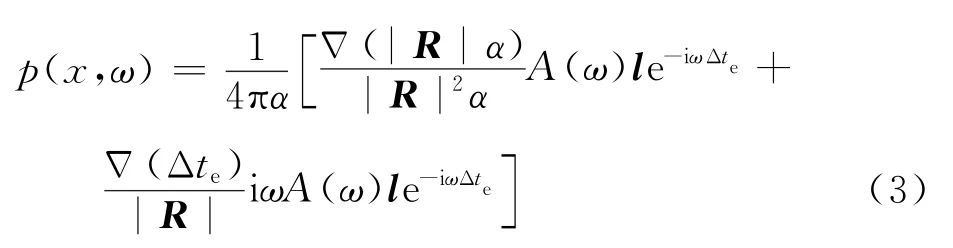
式中:()为偶极子的声压幅值;Δ(·)为拉普拉斯算子。
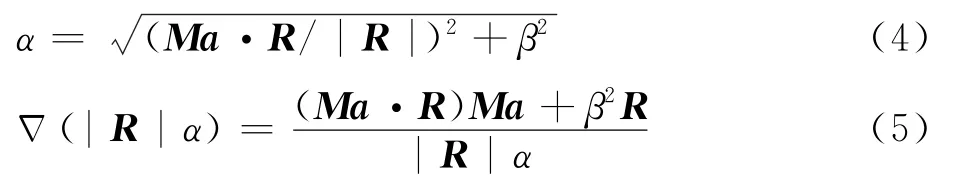
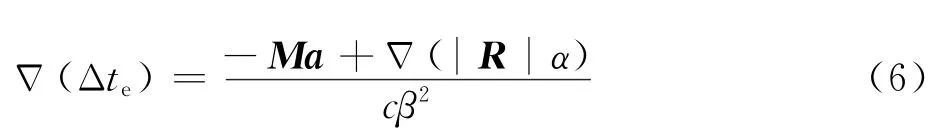
对式(3)进行简化,得
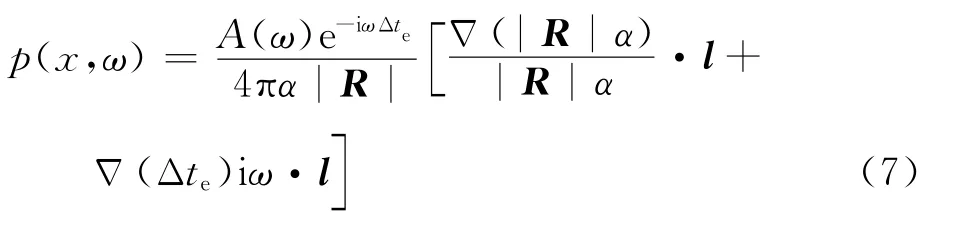
则在直角坐标系下,有稳定流动的偶极子格林函数表示为
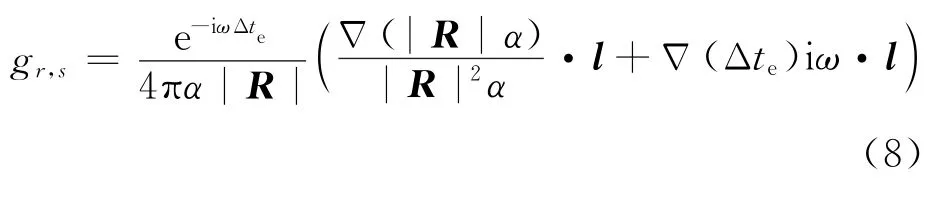
1.2 混合反卷积算法
提出的混合反卷积方法需要在波束成形输出和实际声源分布之间构建一个线性方程组,构建4个点扩散函数矩阵PSF (Point Spread Function):为偶极子波束成形和偶极子源之间的PSF矩阵,为偶极子波束成形和单极子源之间的PSF矩阵,为单极子波束成形和偶极子源之间的PSF矩阵,为单极子波束成形和单极子源之间的PSF矩阵。
计算传播矢量矩阵:
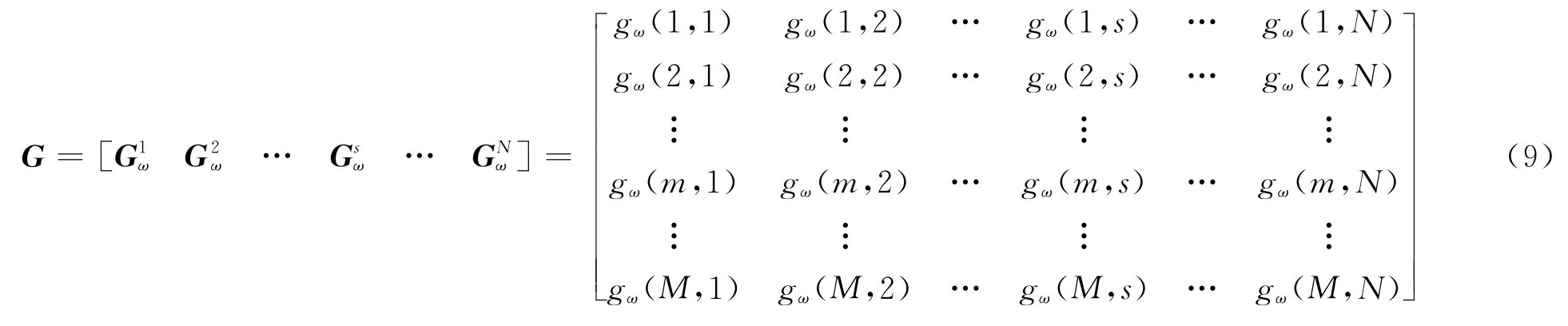
将传播矢量矩阵中的列向量进行归一化,得到导向矢量的列向量

则导向矢量矩阵表示为
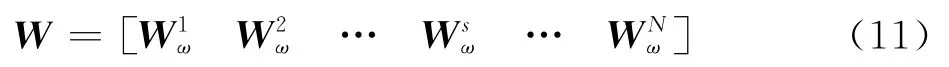
扫描平面上的声压分布用表示,假设声源互相独立,在扫描网格点中设置偶极子声源与单极子声源,其余网格点声压设置为0,为
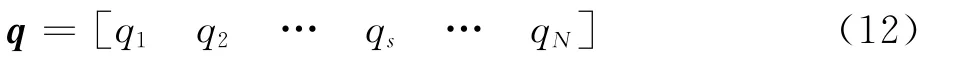
根据传播矩阵,声源信息被传递给了麦克风采集系统,并通过计算机记录成时域信号,接着利用FFT(Fast Fourier Transform)将时域信号转换成频域信号,最后利用式(14)计算出交叉互谱矩阵

传统波束成形输出结果:

式中:上标H 为转置共轭。
将式(13)、式(14)代入式(15),波束成形输出结果可以改写为
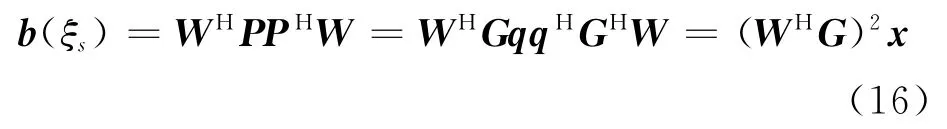
式中:为源强度。传播矢量矩阵携带声学模型信息,导向矢量矩阵携带波束成形信息。
计算混合点扩散矩阵

其中:

式中:为偶极子传播矢量矩阵;为单极子传播矢量矩阵。
构造模拟声源声压分布与波束成形输出结果之间的线性方程组:
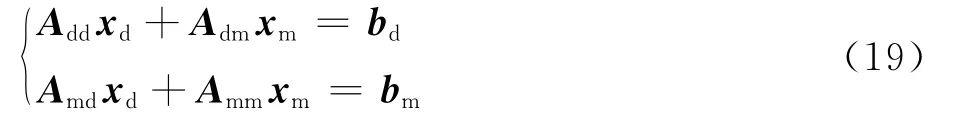
将式(18)代入式(19),混合反卷积线性方程组可以表示为
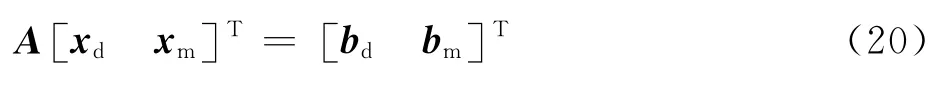
式中:[]为偶极子源和单极子源声压分布的列向量;[]为偶极子波束成形和单极子波束成形输出结果的列向量。
2 仿真设置
设计4个仿真算例,用于验证本文提出的混合反卷积分离算法的有效性。如图1 所示,算例1~算例3设置了由一个单极子源和一个偶极子源组成的双点源,2个声源强度差异分别设置为0、10、-10 d B。算例4考察在多声源状况下该方法的有效性,设置了8个声源,声源强度均为94 d B。假设点源位于扫描平面上,如图1所示,假设单极子源和偶极子源对于组合声源的影响是独立的。扫描平面大小为0.6 m×0.6 m,网格尺寸为0.01 m×0.01 m,共计有3 721个网格点。采用具有40个通道的螺旋麦克风阵列记录压力信号。测量平面与声源扫描平面平行,并放置在距离扫描平面0.6 m 的位置,阵列中心位于轴上。采用DAMAS算法迭代1 000次,并采用文献[14]中的压缩网格方法来提高计算效率。声源分布图所展示的动态范围为20 d B。图1显示了在均匀介质中流动的(0.5,0,0)和偶极子源距离矢量(0,0.02,0)m,所有的算例都在5 k Hz频率下进行研究。
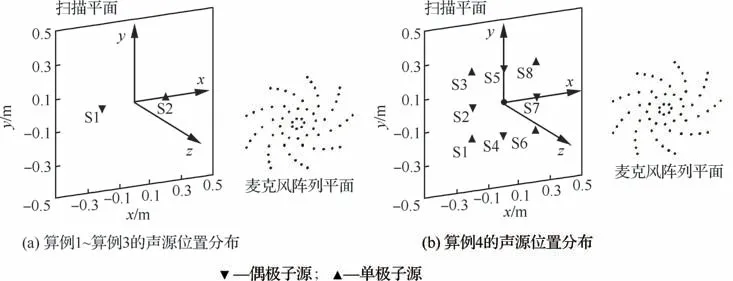
图1 数值仿真声源分布Fig.1 Numerical simulation sources distribution
所使用的仿真点源的声源类型、位置和强度见表1、表2。

表1 双点源分布信息Table 1 Double point sources distribution
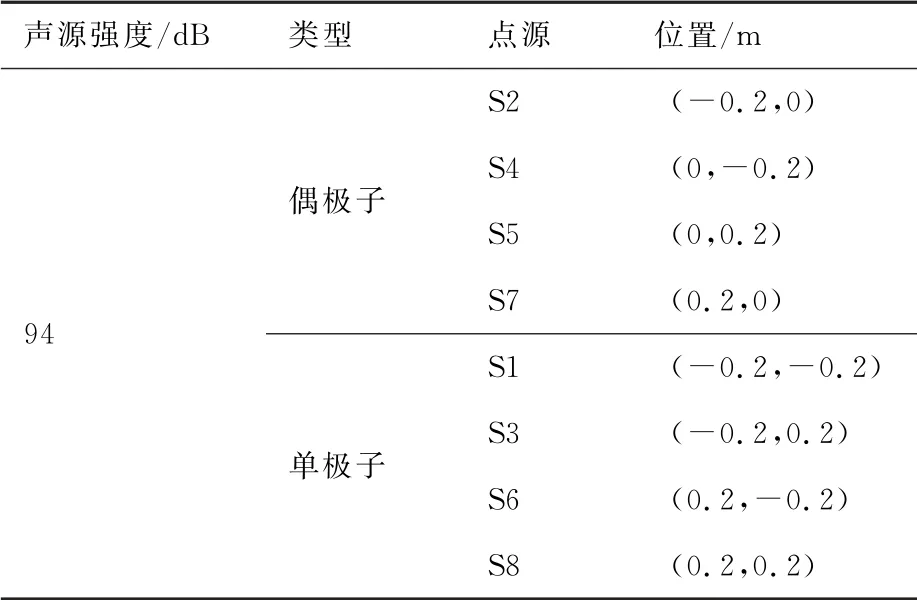
表2 算例4多点源分布仿真信息Table 2 Multi-point sources distribution for Case 4
2.1 双点源等强度分布
算例1中,偶极子源S1与单极子源S2等强度为94 dB,图2展示了不同算法下算例1的声源分布云图,云图中反映强度分布的物理量为声压级(,参考声压取2×10Pa)。图2(a)表示基于单极子假设的波束成形求解结果,单极子源被准确识别出来,偶极子源被抑制,并没有出现。在图2(b)中,可以比较清晰地观察到偶极子的存在,声源强度也基本准确,但是仍然可以在云图上看到单极子源。波束成形的空间分辨率如往常一样比较糟糕,存在大量的伪源。图2(c)、图2(d)利用基于偶极子源和单极子源假设的DAMAS 算法分离组合源,提高云图的分辨率。即使在DAMAS提高了结果云图的空间分辨率后,仍然在图上存在较多的旁瓣。偶极子源和单极子源分别作为干扰噪声出现在对方的云图上,声源的强度误差较小。图2(e)、图2(f)采用本文HD 算法分离组合源。图2(e)展示的单极子声源分布结果,比较准确地分离出了单极子源。图2(f)展示了通过本文HD 算法分离出的偶极子声源分布结果,在声源强度上比较接近预设值94 d B,但在声源位置上存在一定偏差,位置误差为0.01 m。算例1仿真结果表明HD 算法成功地分离了2种等强度分布的不同类型的声源。
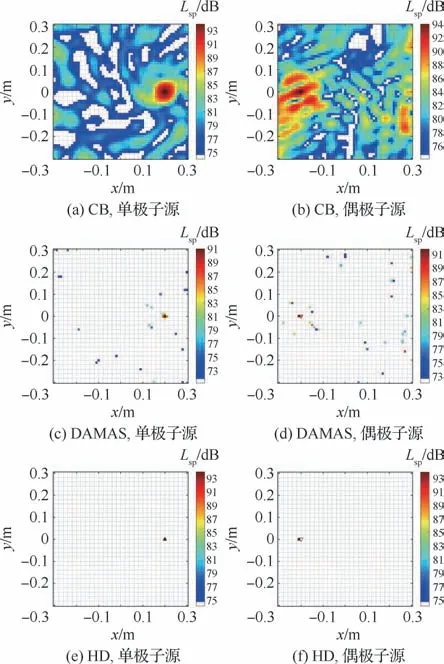
图2 算例1声源定位云图(f=5 k Hz)Fig.2 Sound source localization contour map for Case 1(f=5 k Hz)
2.2 偶极子声源强度占优,S1强度比S2大10 dB
在算例2中,偶极子源的强度比单极子源大10 dB,考察当偶极子源比单极子源强时本文方法的有效性。图3(a)偶极子源基本被过滤掉了,单极子比较清晰地出现在预设的声源位置处,但是周围有比较明显的旁瓣,强度符合预设的84 d B。在由偶极子波束成形计算出的结果云图中,如图3(b)所示最大声源出现在偶极子处,并且同时对单极子源有了很好的抑制作用。DAMAS算法很好地提高了云图的分辨率,在图3(c)中,单极子DAMAS消除了偶极子的旁瓣干扰保持源强,而单极子却被当作偶极子处理并且伴有旁瓣;在图3(d)中,尽管偶极子源作为最大声源被准确识别,但少量的伪源仍然存在分布云图上。本文HD 算法的计算结果如图3(e)、图3(f)所示,在偶极子声源强大比单极子声源强度大的情况下,它可以成功地区分2种不同类型的源,同时保持声源强度的准确性。在位置误差上,图3(f)中偶极子位置存在0.01 m 的偏差。
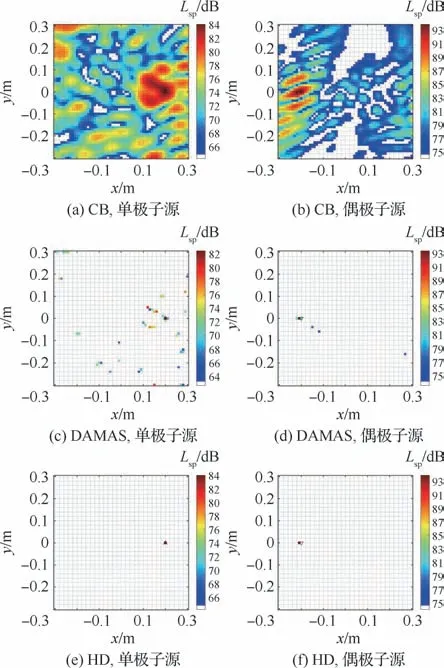
图3 算例2声源定位云图(f=5 k Hz)Fig.3 Sound source localization contour map for Case 2(f=5 k Hz)
2.3 单极子声源强度占优,S1强度比S2小10 dB
算例3与算例2情况相反,偶极子的声源强度比单极子小10 d B,考察当偶极子源比单极子源弱时该方法的有效性。图4(a)中,单极子较完美地从组合声源中被提取出来,保证了定位位置和强度的准确性。图4(b)中,偶极子源被识别为最大声源,周围伴随着较多的旁瓣,强度比预设值大6 d B,单极子附近也存在比较多的旁瓣。从图4(c)、图4(d)可以发现,基于偶极子假设的DAMAS无法有效分离出偶极子声源,而基于单极子假设的DAMAS可以成功分离出单极子声源。利用本文HD 算法分离该算例下的组合声源,成功地将单极子源和偶极子源从组合源中分离开,保持定位强度的准确性展示在各自的洁净声源分布图上,偶极子源的位置仍然有0.01 m的偏差,如图4(e)、图4(f)所示。
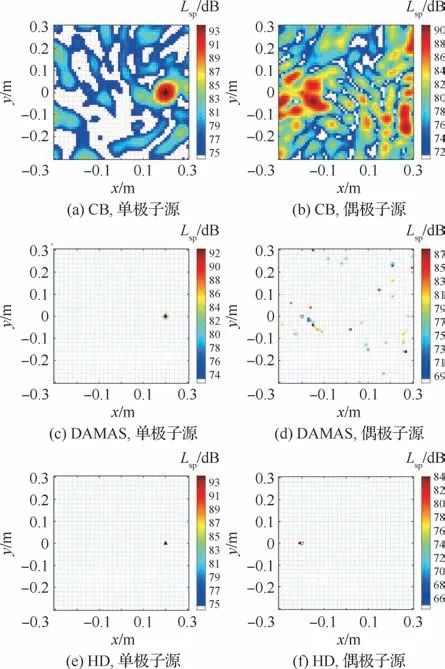
图4 算例3声源定位云图(f=5 k Hz)Fig.4 Sound source localization contour map for Case 3(f=5 k Hz)
2.4 多个声源
算例4设置8个声源,包含4个偶极子源和4个单极子源,考察本文算法在处理多源问题时的有效性。组合声源的位置分布图和类型如图1(b)、表2所示,8个声源强度均为94 dB。在图5(a)中,4个等强度的单极子源可以清晰地被识别出,尽管分辨率较差,但还是很好地过滤了偶极子声源。图5(b)展示了4个偶极子源的位置,整个云图分辨率较差,存在比较多的旁瓣和伪源,有些位置单极子源作为干扰存在。DAMAS算法求解结果如图5(c)、图5(d)所示,尽管DAMAS提高了声源分布图的空间分辨率,但依然存在大量的伪源,所有的声源定位都比较混乱,整个云图结果都比较差。运用本文HD 算法对这8个声源进行分离,预设的点源都可以在图中找到,图5(e)显示了单极子源的分布,可以清楚地观察到声源的强度相差不大,但是在位置上与预设位置存在一定的偏离。图5(f)中的偶极子源分布也比较完美,可以准确清晰地观察预设的4个偶极子,定位位置上还是存在一些偏差。
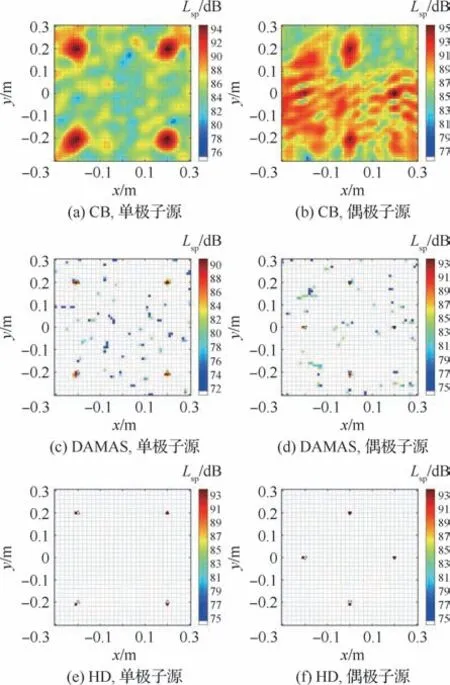
图5 算例4声源定位云图(f=5 k Hz)Fig.5 Sound source localization contour map for Case 4(f=5 k Hz)
3 实验设置
为了进一步验证本文算法,在上海交通大学航空发动机研究院的消音风洞上进行实验验证。通过在喷嘴出口外设置一根平行出口截面放置的均匀圆柱,利用圆柱扰流生成偶极子,并通过放置一个音响作为单极子,从而构造出包含单极子和偶极子的组合声源。实验中的喷嘴出口尺寸25 cm×25 cm,使用的空心不锈钢圆柱直径为6 mm,放置在距离出口截面20 cm 处。采用一个具有64通道的螺旋麦克风阵列,阵列平面与喷流中心线平行,距离1 m,使用了38个麦克风传感器,型号为BK-4958,布置在螺旋阵列前38个通道上。数据采集机箱型号为NI PXle-1082,机箱主板型号为NI PXle-8840,采集板卡为NI PXle-4499,采样频率48 k Hz,持续10 s,频谱计算方法采用Welch法,FFT 分块长度为1 024。扫描平面尺寸1 m×1 m,网格大小为0.02 m×0.02 m,声源分布图动态范围为10 d B。
3.1 实验布置及频谱分析
实验布置如图6(a)、图6(b)所示,分别将不锈钢圆柱横向、纵向布置,依次产生一个向偶极子源和一个向偶极子源,在圆柱中心上方40 cm 处布置了一个音响作为单极子源。首先使用NI(National Instruments)采集器采集环境噪声,接着打开蓝牙音箱播放风扇叶片白噪声,采集单极子的信号,然后启动消音风洞,调整来流速度在110~115 m/s,采集组合声源的信号,关闭音箱,采集偶极子信号,最后逐步减小流速,关停风洞。
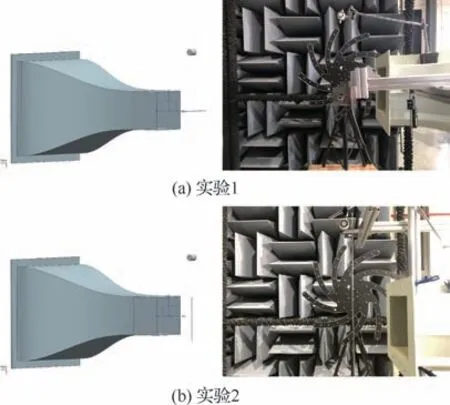
图6 现场声源分布Fig.6 Sound source distribution
分别对以上2 种布置进行频谱分析,由于FFT 的结果是复数,伴随着相位,因此对于38个麦克风通道不能进行简单的线性平均,这里采用的是几何平均,对个通道的积求次方根,几何平均频谱如图7、图8所示。
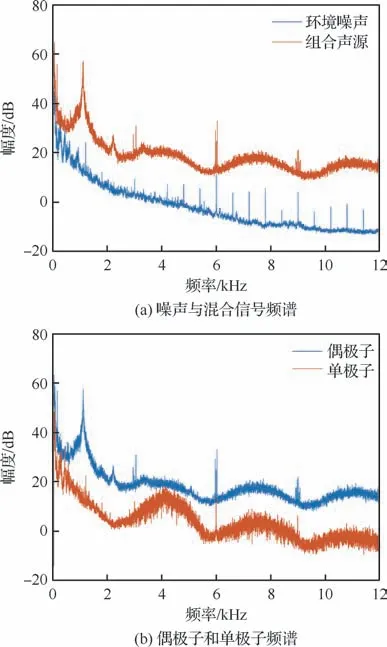
图7 实验1频谱图Fig.7 Spectrum for Experiment 1
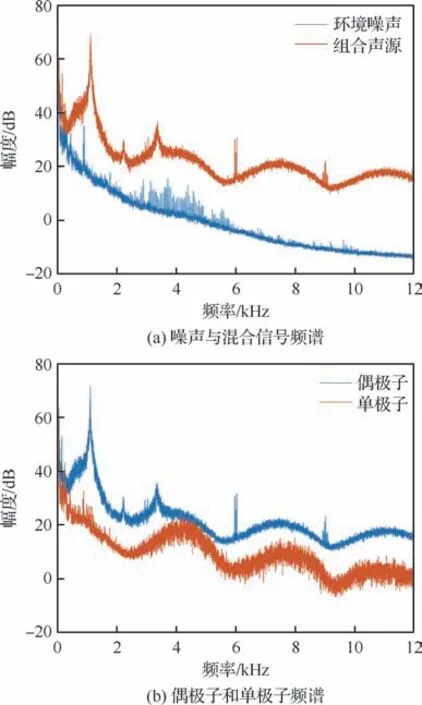
图8 实验2频谱图Fig.8 Spectrum for Experiment 2
不难发现,偶极子声源在组合声源中占优,已知圆柱直径、气流速度,根据斯特劳哈尔数可以推算出圆柱绕流产生的偶极子发声频率在3 200 Hz左右,与频谱图大致吻合,此外在实际测试过程中还发现在3、6、9 k Hz下存在较明显的尖峰纯音凸起,应是风洞变频器干扰噪声,在1 k Hz附近也出现了一个较大的干扰,应是本实验中采用的风洞喷嘴出口以及夹具与气流产生的干扰噪声。下面对采样信号进行声源定位,分析频率选取采样信号声源强度最大的频段1 k Hz,考虑到波束成形算法在低频下的低分辨率与混叠现象,又选取宽频5 k Hz下的结果进行对比。
3.2 声源定位云图
图9~图12 分别为选取中心频率1、5 k Hz时对2种偶极子布置的声源定位结果。通过对频谱分析可知,信号的最大声源在1 k Hz左右,因此选取了1 k Hz作为分析频率。首先看圆柱横向布置,即偶极子的指向性为轴,CB 对偶极子进行了分离,尽管存在分辨率较差的情况,而对于单极子的识别中,未能消除偶极子对单极子定位的干扰。DAMAS 对于组合声源进行了有效分离,在各自的定位云图上都消除了对方的干扰,但是定位出来的声源位置有较大的误差,并且存在伪源。HD算法对DAMAS的结果进行了优化,声源的定位位置精度有了提高,并且旁瓣、伪源抑制能力有了改善。对于圆柱纵向布置的情况,即偶极子指向性为轴,由于圆柱竖放时,气流打在杆上形成了一条线性声源,声源强度可能超过单极子声源强度,在此分析频率CB、DAMAS以及HD都没有能够有效分离组合声源。
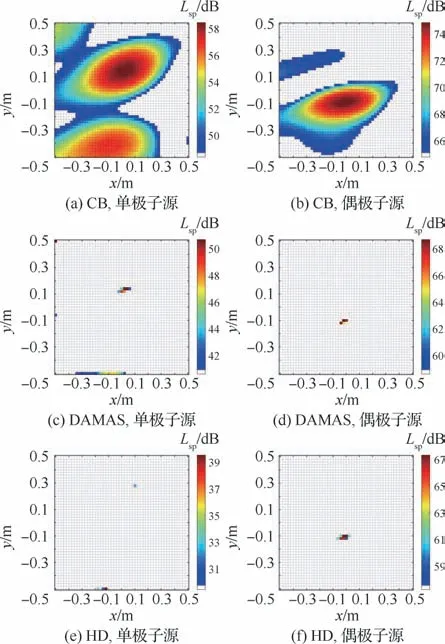
图9 实验1声源定位云图(f=1 k Hz)Fig.9 Sound source localization map for Experiment 1(f=1 k Hz)
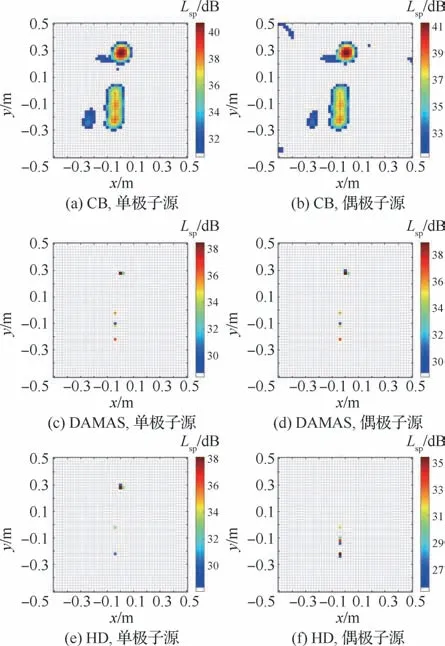
图12 实验2声源定位云图(f=5 k Hz)Fig.12 Sound source localization map for Experiment 2(f=5 k Hz)
对于宽频5 k Hz的分析频率,当圆柱横向放置时,随着频率的升高,各个算法的分辨率有了显著的提升。CB比较清晰地定位了偶极子,但是并未消除单极子的干扰,而在单极子的定位中,由于偶极子的强度较大,将偶极子误判为最大的声源。DAMAS 提升了CB 的分辨率和动态范围,但是无论在识别单极子还是识别偶极子都未能削弱对方的干扰,2个声源都比较清晰地被定位出。HD 改善了DAMAS的结果,在定位偶极子的同时尽可能的消除了单极子,而对于识别单极子中存在的较强偶极子也进行了一定的削弱。当圆柱竖直放置时,由于声源与阵列的相对位置影响,CB将偶极子识别成了一个线性声源,对于偶极子和单极子的定位相差不大。DAMAS反映的是CB结果在分辨率与动态范围的改善,但是对于次声源的消除表现一般,在偶极子与单极子云图上都可以清晰地看见2个声源。HD 算法进一步优化了DAMAS结果,准确定位偶极子的同时消除了单极子,尽管在定位单极子时没有能够完全消除偶极子,但是相较于DAMAS对单极子的定位结果已经有了改善。
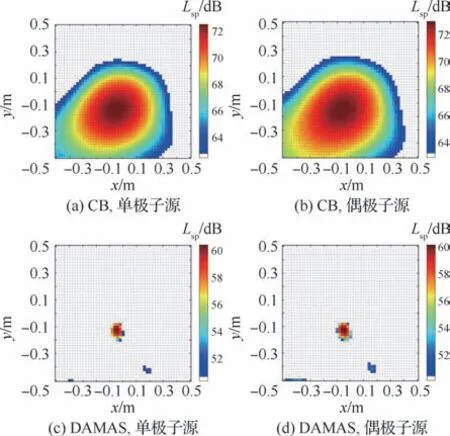
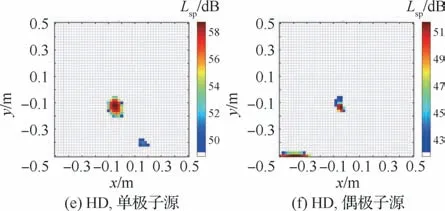
图10 实验2声源定位云图(f=1 k Hz)Fig.10 Sound source localization map for Experiment 2(f=1 k Hz)
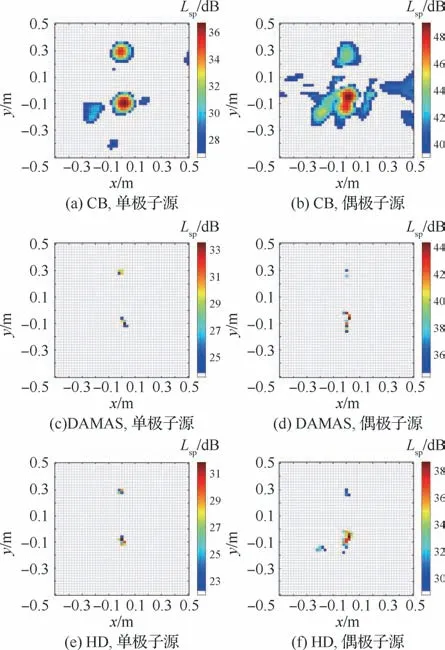
图11 实验1声源定位云图(f=5 k Hz)Fig.11 Sound source localization map for Experiment 1(f=5 k Hz)
4 讨 论
基于DAMAS设计了一种混合反卷积算法,通过螺旋麦克风阵列测量将单极子源和偶极子源相结合的声源分离开来。在对声源类型的假设处理中,还存在以下问题:
1)偶极子指向性。本文方法侧重于分离单极子声源和已知指向性的偶极子声源,例如风扇旋转造成的旋转偶极子声源,如何分离单极子和未知指向性的偶极子声源,将是未来的一个研究方向。
2)声源的相干性。本文方法是基于假设单极子声源和偶极子声源相互独立的,尚不能处理存在较强相互干涉的组合声源。未来本文方法有望通过建立四极子模型应用于喷流噪声的成分识别,但是由于真实喷流中各声源之间存在较强大的相互干渉,因此将来有必要对如何分离具有相互干涉的声源进行深入研究。
5 结 论
提出了可以实现单极子源和偶极子源分离的方法,这是当前基于单一声源类型假设的波束成形算法和DAMAS 算法所不能做到的。本文方法建立在各类型声源相互独立的基础上,在构造线性方程组的时候,同时考虑了单极子源和偶极子源的输出,通过求解该方程组的解得到了单极子和偶极子的声源分布。仿真和实验证明,本文方法不仅可以在原始网格上显示不同类型声源的分布,而且可以保持较低的定位位置偏差和强度估计误差。即使在处理较多声源时,也能较好地区分开不同类型的声源并且保持较明显的源强差异。尽管混合反卷积算法被证明是分离由单极子和偶极子组成的组合源的有效方法,但在定位偶极子源过程中仍然存在很小的偏差。
本文方法有望应用于航空发动机气动噪声识别。航空发动机的喷流噪声常常由单极子、偶极子及四极子源组成,通过在混合反卷积中添加四极子声源模型,有望从喷流噪声提取目标源,以加深对喷流噪声产生机理以及后续降噪设计的研究。
