电动载货汽车整车质量及质心位置估计

李航宇，倪骁骅，郑精干，张森

（224051 江苏省 盐城市 盐城工学院）

0 引言

目前对汽车的主动安全控制通常基于固定的惯性参数，但载货汽车的质量以及质心位置因载重不同而变化较大，若仍使用固定参数，必然存在极大的安全隐患，因此对载货汽车的质量和质心位置进行实时估计非常必要。电动载货汽车随着我国物流行业迅猛发展被广泛应用[1]，使用电驱动汽车易获得的驱动力参数对整车质量进行估计，可极大提高估计的准确性。

车辆的质量估计通常是基于车辆的纵向运动学来完成的。MALEEJ[2]等人使用带遗忘因子的RLS 算法对汽车质量进行了估计，取得了较好估计效果。MAHYUDDIN[3]等人设计了一种带有滑模项的参数估计方案，在无需得知汽车加速度的情况下即可估计整车质量。CHEN[4]等人针对四轮驱动小型车辆，通过估计车轮的垂直力进而得出了整车质量，由于轮胎模型的复杂性，其质量估计准确性不高。褚文博[5]等人解耦质量与坡度间的关系，获取驱动力与加速度的高频值对质量进行估计，并进行了实车验证。在所有车辆参数中，质心的纵向位置和高度是两个重要参数。HUANG[6]等人针对小型四轮驱动车辆，在不广泛激发车辆运动的情况下，对车辆质心的位置进行了估计。付志军[7]等人运用参数误差信息驱动的方法对载重汽车的质心高度进行了估计。在车辆的质量估计中，大多数研究都需预先知道空气阻力系数、滚动阻力系数等才能对质量进行估计，在实际应用中，由于不同道路环境的影响，其估计准确性有所降低。对于质心位置估计国内研究较少。

本文在分析纵向动力学模型后，将坡度、速度与质量解耦，建立了纵向驱动力、纵向加速度和质量的动力学关系，运用跟踪微分器对汽车驱动力及加速度信号进行预处理，再运用卡尔曼滤波法对整车质量进行了估计。在估计的质量基础上，建立了低滑移率下的线性轮胎模型，运用递归最小二乘法对质心的纵向位置进行估计。

1 基于跟踪微分器与卡尔曼滤波的整车质量估计

1.1 纵向动力学模型分析

汽车的纵向运动学方程如式(1)：

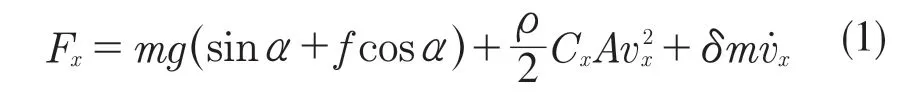
式中：Fx——驱动力；m——整车质量；g——重力加速度；α——道路坡度；f——滚动阻力系数；ρ——空气密度；Cx——风阻系数；A——迎风面积；vx——车辆纵向速度；δ——旋转质量换算系数；——汽车纵向加速度。

式（1）对纵向加速度进行微分可得式（2）：

假设在行驶过程中，加速度的变化率远大于坡度的变化率，则有式（3）：

当驱动力较大时，加速度的变化率要远大于速度的变化率，则有式（4）：

经上述处理后，式（2）可简化为式（5）：

1.2 跟踪微分器设计

由式（5）可知，求解质量m需计算d/dt与dFx/dt。由于、Fx的获得存在噪声扰动，使用经典微分器会将噪声放大，因此本文使用跟踪微分器求解d/dt、dFx/dt。跟踪微分器（TD）[8]是“自抗扰控制器”（ADRC）[9]的组成部分。传统信号微分是通过经典微分器获得，在跟踪微分器中，改用振荡环节取代原本的惯性环节[10]。

运用跟踪微分器的构建方法，对加速度的导数进行求解，建立式（6）：

式中：r0，h0——函数控制参量。r0越大，可更快地跟踪信号，调节h0能改变滤波效果[11]；a1，a2，sy，a，sa——函数内部参数。

运用跟踪微分器的构建方法，对驱动力的导数进行求解，建立式（8）：

1.3 卡尔曼滤波法设计

运用跟踪微分器对数据进行预处理后，使用卡尔曼滤波法对质量进行估计。选择质量m作为状态变量，则系统状态变量为xk=mk，建立离散方程如式（9）。

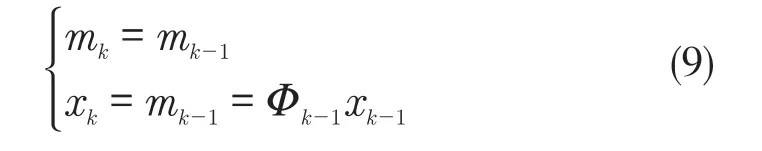
式中：Φ——状态转移矩阵。

建立量测模型式（10）：

式中：Γ——状态噪声系数矩阵；Qk-1——状态噪声协方差矩阵；Pk（-）——基于状态模型的协方差递推矩阵。

按照递推滤波器的架构，构建量测修正估计式（13）：

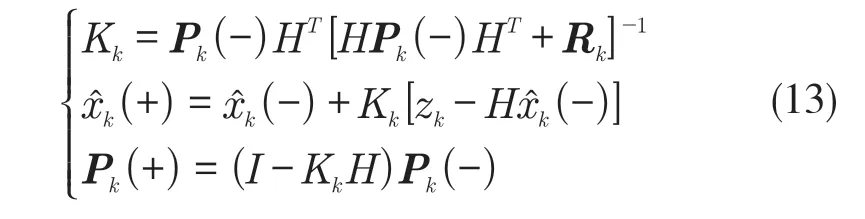
式中：Kk——卡尔曼增益；Pk（+）——基于量测模型的协方差递推矩阵；Rk——量测噪声协方差矩阵。

2 基于递归最小二乘算法的质心位置估计

2.1 载货汽车动力学模型

图1 表示车辆纵向运动模型。本文未考虑悬架的动力学，因此将簧上质量与簧下质量视为整体。依据三自由度车辆动力学模型建立前后轮垂直力求解方程如式（14）。

图1 带有车轮的三自由度车辆动力学模型Fig.1 Three degree of freedom vehicle dynamics model

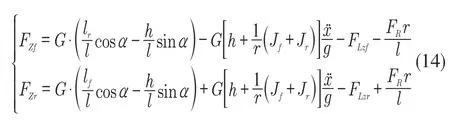
式中：FZf，FZr——前、后轮垂直力；忽略前后轮滚动半径差异，令滚动半径为r；l——汽车的轴距；lf，lr——质心至前、后轴的距离；h——质心的高度；G——整车重量；α——道路坡度；Jf，Jr——前、后轮转动惯量；FLzf，FLzr——前、后轴空气升力，在速度较低时可忽略；FR——滚动阻力，对垂直力影响很小，可忽略不计。

2.2 车轮模型

车轮的附着率定义如式（15）：

式中：Fx——车轮切向力；Fz——车轮垂直力。

车轮的滑移率定义如式（16）：

式中：ωi——车轮的转动角速度；ri——车轮的滚动半径；v——汽车纵向速度。

车轮附着率u是滑移率s的函数。当滑移率s≤0.05 时，u与s可近似为线性关系[12]，如式(17)：

2.3 质心位置估计流程

图2 为质心位置估计流程，传感器获取发动机扭矩以及前后轮角速度信号，然后计算驱动轮滑移率、驱动力。当滑移率满足0＜s≤0.05 时，依据附着率u与滑移率s线性关系计算轮胎垂直力Fz。将垂直力与估计的质量作为输入参数，依据垂直力求解方程式（14）对质心位置进行估计。

图2 质心位置估计流程Fig.2 Centroid position estimation process

2.4 递归最小二乘法设计

本文使用递归最小二乘法对质心位置进行估计。式（18）为带量测噪声的量测模型。

式中：x——带估计参数；zi，Hi——输入参数；vi——量测噪声。

式（19）为目标函数，传统的最小二乘法通过使J取得最小值，求得待估计参数。

递归最小二乘法对式（19）进行了改进，将批处理算法改为了递推法，方便计算以及实时估计。式（20）为递推最小二乘法公式。

考虑道路坡度等于零，即α=0，忽略滚动阻力对前轮垂直力的影响，即FR=0，将式（14）转换为最小二乘法估计的标准形态式，如式（21）：

3 仿真与结果

建立CarSim/Simulink 联合仿真模型，采集CarSim 信号作为传感器输出信号，在Simulink 中进行实时估计运算。为确定质量估计方案的适用范围，在CarSim 中设定了固定坡度路面与正弦扫频路面下的仿真。

3.1 固定坡度路面质量估计

在CarSim 中设定固定坡度道路模型，坡度为5%，仿真使用车辆为前轮驱动，采样时间设定为0.01 s，仿真时长为6 s，仿真工况为半油门起步工况。表1 为仿真车辆的部分参数。由前面分析可知，质量估计在驱动力以及加速度变化大时估计结果更为准确，因此设定在仿真过程中加加速度满足式（22）时才进行质量估计运算。

表1 车辆模型部分参数Tab.1 Partial parameters of vehicle model

式中 ：——加加速度观测值。

图3 为仿真过程中车辆纵向速度以及驱动轮滑移率曲线。由于车辆刚起步阶段，车轮滑移率变化过大，影响估计准确性，因此设定车速已经达到后再运行质量估计程序。

图3 车速及滑移率Fig.3 Speed and slip ratio

为使仿真更接近于真实情况，在CarSim 输出的加速度以及驱动力信号中加入随机噪声，运用跟踪微分器对加速度及驱动力信号进行预处理。图4为跟踪微分器对加速度信号处理结果，图5 为跟踪微分器对驱动力信号处理结果。从图5 可见，使用传递函数为s/（Ts+1）普通微分方式极大地放大了传感器噪声，使用跟踪微分器进行微分的数据平滑。

图4 固定坡度路面加速度信号处理结果Fig.4 Acceleration signal processing results of fixed slope pavement

图5 固定坡度路面驱动力信号处理结果Fig.5 Driving force signal processing results of fixed slope pavement

图6 为固定坡度路面质量估计结果。整车质量的估计值为2 036 kg，在CarSim 中设定车辆的实际质量为2 000 kg，可以计算估计误差为1.8%。

图6 固定坡度路面质量估计结果Fig.6 Mass estimation results of fixed slope pavement

3.2 正弦扫频路面质量估计

在CarSim 中建立正弦扫频路面，如图7 所示。其余参数相比固定坡度路面仿真不发生改变。图8为扫频路面的质量估计结果，整车质量的估计值为2 014 kg，可以计算估计误差为0.7%。

图7 正弦扫频路面Fig.7 Sinusoidal sweep pavement

图8 扫频路面质量估计结果Fig.8 Estimation results of swept frequency pavement mass

分析固定坡度路面与正弦扫频路面的质量估计结果，可知本文设计的质量估计方法成功将质量与坡度、空气阻力、滚动阻力解耦，在无需得知道路坡度、空气阻力系数、滚动阻力系数的情况下即可对质量进行估计。

3.3 质心位置估计

质心的位置估计在道路坡度为零的条件下进行，其余参数设置与质量估计时相同。仿真选用的轮胎模型185/65 R15，轮胎在0＜s≤0.05 时，kx=29.2。

质心位置估计需要先对整车质量进行估计，有了质量估计参数后再代入质心位置估计模型对质心位置进行估计。图9 为质量估计结果，整车质量的估计值为1 991 kg。

图10 为质心纵向位置估计结果。质心位置估计在仿真接近3 s 时才开始，这是因为前期不满足0＜s≤0.05 的条件。结合图9，可知此时的质量估计值已稳定。质心至前轴距离的估计值为1.515 m，在CarSim 中设定实际值为1.5 m，可以计算估计误差为1%。

图9 质量估计结果Fig.9 Mass estimation results

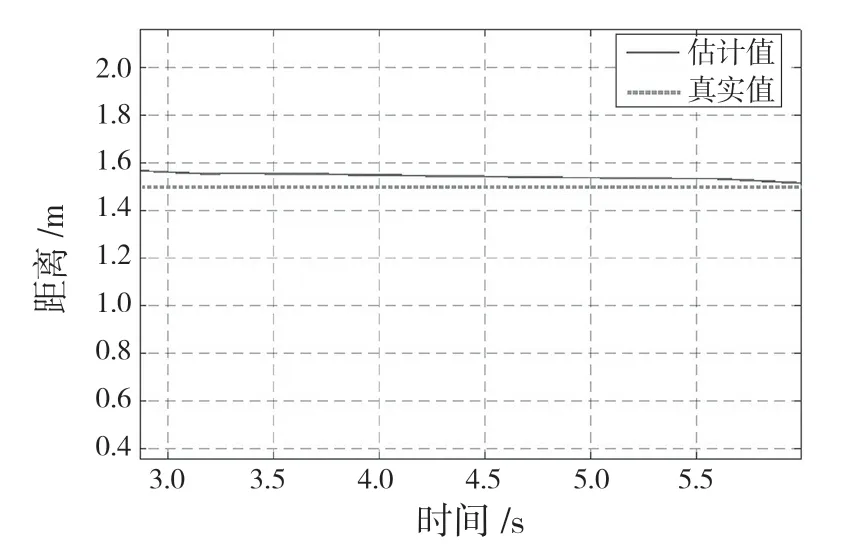
图10 质心纵向位置估计结果Fig.10 Estimation results of longitudinal position of centroid

整车质量估计误差的存在会导致质心位置估计的误差放大，但在整车质量估计误差不超过2%的情况下，可以验证纵向质心位置的误差仍然较小。

4 结语

解耦质量与坡度、风阻、道路阻力的关系，在无需知道道路坡度、空气阻力系数、滚动阻力系数的情况下对质量进行估计。运用跟踪微分器对加速度、驱动力信号进行处理，抑制了因传感器噪声导致的微分误差放大，随后使用卡尔曼滤波法对质量进行估计。在估计质量基础上，考虑车轮在低滑移率下，附着率与滑移率所拥有的线性关系，通过滑移率、驱动力计算得到车轮的垂直载荷，运用递归最小二乘法对电动载货汽车的质心纵向位置进行了估计。采用CarSim 与MATLAB/Simulink 进行了联合仿真，结果表明：（1）在固定坡度路面及正弦扫频路面下质量估计误差皆小于2%。（2）因质量估计存在误差，会导致质心位置估计的误差放大，但从仿真结果可以得到，质心纵向位置估计结果误差仍小于2%。