爆胎车辆动力学分析及稳定性控制

吴奕滨，臧利国，王星宇，王智，李瑶薇

（1.211167 江苏省 南京市 南京工程学院 汽车与轨道交通学院；2.25009 江苏省 扬州市 扬州大学 机械工程学院；3.250357 山东省 济南市 运输车辆检测、诊断与维修技术交通行业重点实验室）

0 引言

轮胎是车辆与路面接触的唯一部件，对于支承车身、缓和外界冲击、保证车辆的行驶性能有着不可缺少的作用。爆胎轮胎力学特性的突变，会导致车辆出现侧倾、横摆、偏航甚至是甩尾等危险工况，危害行车的安全性[1]。近年来，大约有46%的交通事故是由轮胎引起，且其中70%以上的事故是由于爆胎引起的[2]。相关统计数据显示，近32%的高速公路事故均由爆胎引发，死亡率接近49%，且高速行驶时，爆胎导致车毁人亡的概率近80%[3]。

鉴于爆胎造成的巨大危害，国内外学者对此进行了大量的研究和讨论，取得了不少的进展和成效。王英麟[4]通过轮胎实验，测得爆胎后轮胎的垂向刚度、纵滑刚度、侧偏刚度均明显降低，而滚动阻力系数则明显上升；Orengo[5]针对轮胎冲上路肩和车辆行驶在颠簸路面等情况建立了轮胎有限元模型，预测并验证了各工况下爆胎轮胎的最终形态。周景宇[6]等将轮胎简化为串联弹簧系统，建立爆胎车辆模型，对车辆的侧向加速度、横摆角速度和车身侧倾角的变化进行分析，得到了车辆偏航的原因；Sassi[7]等基于九自由度模型分析，研究了车辆爆胎后的动力学特性，得到车辆重心的偏移、操作条件及轮胎与道路的相互作用的变化都会改变侧向加速度，使车辆失去稳定性偏离其原轨道；刘维[8]等设计了模糊滑模控制算法和制动力分配策略，用于控制车辆的横摆力矩。仿真表明，该控制器对爆胎车辆的行驶轨迹进行了有效控制，同时显著提高了爆胎车辆的稳定性；于树友[9]等建立了以控制参数MAP 为基础的变增益PID 控制器。仿真结果表明，此控制器能有效解决爆胎车辆的失稳问题和减少车辆的偏航量，并使车辆回归原轨迹行驶；Al-Quran[10]等提出了一种基于制动/牵引驱动的自动纠偏安全控制器设计与评估方法，有效提高了爆胎后车辆的稳定性。

基于爆胎轮胎各参数的变化，本文以UniTire轮胎模型为基础，在Simulink 中建立了爆胎轮胎模型，并结合CarSim 软件建立了爆胎整车动力学模型，仿真分析了直线行驶时爆胎车辆的动力学响应，以及不同车速与不同载重对车辆运动状态的影响。提出了基于模糊滑模控制算法和模糊PID 控制算法的外环轨迹控制—内环差动制动控制联合控制策略，以直行左前轮爆胎工况为例，验证了所设计的控制器的有效性。

1 爆胎轮胎及车辆模型

UniTire 轮胎模型的总切力和回正力臂Dx表达式如式（1）所示。

式中：E——曲率因子；Dx0——初始力臂；De——终了力臂；D1、D2——1 次、2 次曲率因子。

轮胎的纵向力、侧向力回正力矩及滚动阻力矩表达式（2）所示。

式中，Xc、Yc——由纵向力和侧向力产生的轮胎形变量；Rr_c、Rr_v——轮胎的滚动阻力系数和滚动阻力速度常数；Vr——轮心纵向速度（Vr=Ω·Re）；Rl——轮胎负载半径。

为简化建模，认为爆胎瞬时完成，轮胎各参数线性变化。爆胎过程中，轮胎的纵滑刚度Kx、侧偏刚度Kv、滚动阻力系数Rr_c和有效滚动半径Re的变化可如式（3）所示。

式中：Kx0——正常轮胎的纵滑刚度；Ky0——正常轮胎的侧偏刚度；Rr_c0——正常轮胎的滚动阻力系数；Re0——正常轮胎的有效滚动半径；Td——爆胎持续时间；Ts——爆胎突发时间。

所用规格为37×12.5R16.5LT 的轮胎，在车辆动力学仿真软件CarSim 中选用E-Class、SUV 车辆，对车身及轮胎等各子系统进行设置，最终完成CarSim/Simulink 联合仿真平台的搭建。

2 爆胎车辆的动力学响应

2.1 直行工况下爆胎车辆的动力学响应

考虑到直线行驶时车辆的对称性，为简化分析，选用一侧前后车轮分别进行爆胎仿真实验。工况设置：车辆纵向速度100 km/h，路面附着系数0.85，爆胎后无驾驶员干预，仿真时长为10 s，爆胎突发时刻为第3 s。爆胎车辆参数变化如图1所示。

由图1（a）可知，在直行工况下爆胎后，车辆向爆胎车轮一侧发生偏航，且侧向偏移量较大，不采取任何措施的情况下，车辆将很快脱离原轨道，撞向护栏；由图1（b）—图1（d）可知，爆胎后短时间内，车辆的侧向加速度、质心侧偏角以及横摆角速度达到最大值，并均在爆胎1.7 s 后趋于稳定。比较前后轮爆胎后的参数变化可得，后轮爆胎偏航量较前轮爆胎更小，其各项参数的峰值和稳定值均比前轮爆胎更小，后轮爆胎较前轮爆胎车辆的运动状态更为稳定。

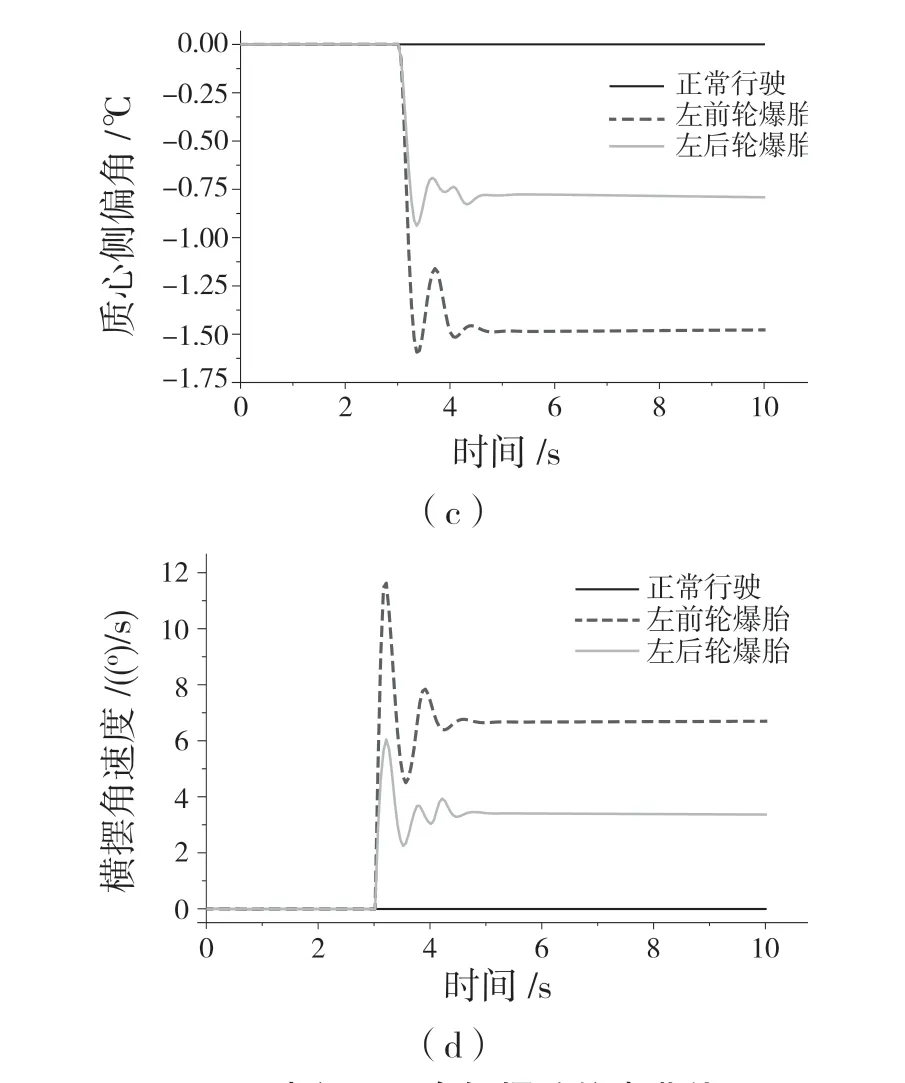
图1 直行工况车辆爆胎仿真曲线Fig.1 Simulation curve of vehicle tire blowout under straight driving condition

2.2 直行工况不同车速下爆胎车辆的动力学响应

考虑到车速对车辆行驶稳定性的影响，选取不同车速分别进行爆胎仿真实验。车辆以不同车速直线行驶时，左前轮爆胎各参数变化如图2 所示。

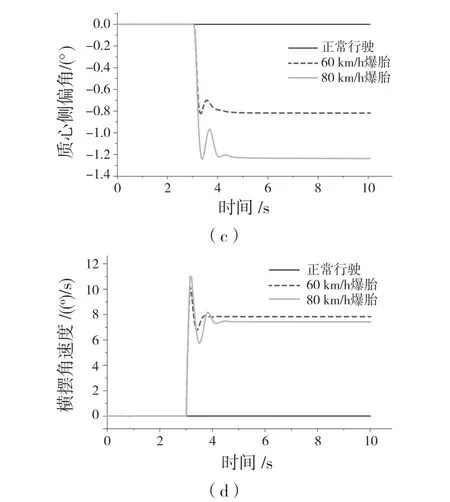
图2 不同车速直行时左前轮爆胎仿真曲线Fig.2 Simulation curve of left front tire blowout when going straight at different speeds

综合图1 和图2 可得，直行工况下，不同车速的左前轮爆胎车辆各参数的变化规律具有相似性。爆胎后车辆的偏航量、侧向加速度和质心侧偏角与正常值的偏差随车速的增加而增加，但此时横摆角速度却随着车速的增加而减少。

2.3 直行工况不同载荷下爆胎车辆的动力学响应

考虑到载荷对车辆行驶稳定性的影响，选取不同簧载质量分别进行爆胎仿真实验。车辆以不同载荷直线行驶时，左前轮爆胎各参数变化如图3 所示。

综合图1 以及图3 可得，直行工况下，不同载荷下的左前轮爆胎各参数的变化规律具有相似性。爆胎后车辆的偏航量、侧向加速度、质心侧偏角和横摆角速度与正常值的偏差随载重的增加而减少。载荷越大，爆胎后期车辆各运动参数愈发不稳定。

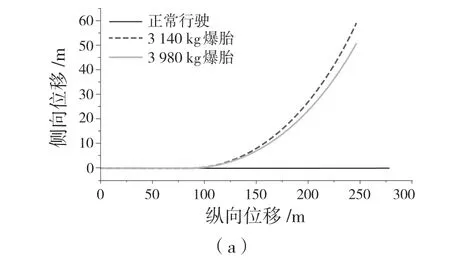
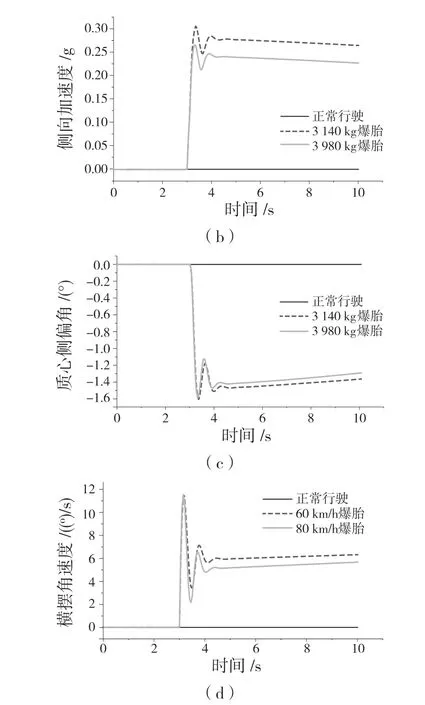
图3 不同载重下直行时左前轮爆胎仿真曲线Fig.3 Simulation curve of left front tire blowout when going straight under different loads

3 爆胎车辆稳定性控制策略

3.1 车辆二自由度模型

为了便于分析车辆运动状态与稳定性之间的关系，对车辆模型进行了简化，将车辆二自由度模型作为理想的车辆运动模型。

考虑到作用在车辆附加横摆力矩的影响，理想的二自由度模型表达式为：

式中：Vx——车辆沿X轴方向的速度；m——车辆总质量；β——质心侧偏角；r——横摆角速度；δ——前轮转角；a，b——质心到前后轴的距离；Iz——整车绕坐标系Z轴的转动惯量；Cf，Cr——前轴、后轴的等效侧偏刚度；ΔMZ——附加横摆力矩。

考虑到路面附着系数μ的影响，理想的横摆角速度以及质心侧偏角的表达式修正为

式中：K——车辆稳定性系数，L——前后轮之间的轴距；g——重力加速度。

此外，爆胎后车辆的实际偏航值计算公式：

式中：ψ——车辆的横摆角观测值，可由观测到的横摆角速度积分得到。

3.2 差动制动控制

差动制动控制采用模糊滑模控制算法得到在爆胎过程中为保持车辆稳定性所需的横摆力矩。滑模控制器滑模面的切换函数的表达式如式（7）。

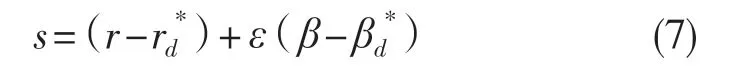
式中：ε——加权系数，一般取正数。

为了增强控制系统的抗干扰能力，提高系统的稳定性，采用饱和函数sat（s/τ），其中τ为系统的边界层厚度，整理可得滑模控制器输出的横摆力矩的表达式为

以质心侧偏角的差值Δβ和横摆角速度的差值 Δr作为模糊控制器的输入量，设输出量为U。通过模糊控制算法可得维持车辆稳定性的补偿横摆力矩ΔMZ2的关系式为

由此可得在爆胎过程中为维持车辆稳定性所需的横摆力矩为

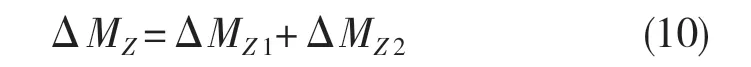
选用制动轮时，应尽量选择制动效率最大的一组轮胎作为制动轮。当横摆力矩的符号为正时，采用爆胎轮胎的对角轮作为主制动轮，同轴异侧轮作为从动轮。当横摆力矩的符号为负时，选用未爆胎的轮胎作为制动轮。

3.3 主动转向控制

主动转向控制采用模糊PID 控制算法，以车辆未偏航的正常行驶轨迹与爆胎后车辆偏航后的实际轨迹的差值e及其变化率ec作为控制算法的输入变量，输出方向盘转角。

通过模糊控制对PID参数实时调整后，其比例、积分及微分参数的值变为

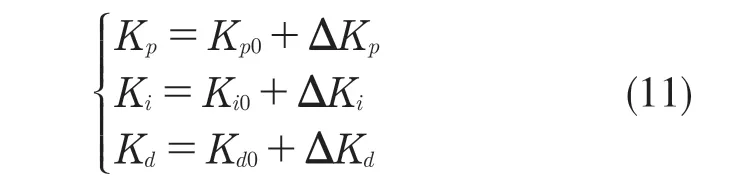
式中：Kp0，Ki0，Kd0——PID 参数的预整定值。

之后，由式（12）即可得到方向盘转角。

式中：y（t）——方向盘转角；e（t）——差值信号。

3.4 联合控制

考虑到单一控制都存在一定的局限性，将两种方法结合设计了爆胎车辆联合控制系统，外环为轨迹控制，内环为差动制动控制，使爆胎车辆能够按预定的轨迹稳定行驶。参见图4。

图4 爆胎稳定性控制流程图Fig.4 Flow chart of tire blowout stability control

4 稳定性控制分析

为验证设计的控制方法的有效性和正确性，基于已建立的整车联合仿真模型，对直行左前轮爆胎分别进行单一差动制动、单一主动转向和联合控制。

工况设置：车辆纵向速度为100 km/h，路面附着系数为0.85，仿真时长为10 s，左前轮爆胎突发时刻与控制器生效时间均在第3 s，爆胎后驾驶员无任何操作。控制仿真结果如图5 所示。

4.1 制动控制

由图5 可得，未经控制时车辆的侧向最大位移量为70 m。经制动控制后，侧向位移量下降至2.35 m，仅为未经控制时的0.033%。由高速公路标准车道宽为3.75 m，可得此时车辆未完全驶入另一车道。制动控制能有效控制直行左前轮爆胎车辆的侧向位移，但汽车车速明显下降，其纵向位移减小为177 m，仅为正常行驶时的48.4%，若后车在爆胎发生后，仍以100 km/h 的车速行驶，极易撞向爆胎车辆，发生交通事故。

图5 直行工况左前轮爆胎控制仿真曲线Fig.5 Simulation curve of left front tire blowout control under straight driving condition

4.2 转向控制

由图5 可得，经转向控制后，侧向位移下降至2.18 m，较制动控制略微下降，且此时车辆的纵向位移为256 m，不易发生追尾等交通事故。转向控制能有效控制直行左前轮爆胎车辆的侧向位移，同时较好地控制车辆的各运动参数，使车辆稳定行驶，但在控制的前中期，车辆会左右横摆，稳定性明显下降。

4.3 联合控制

由图5 可得，经联合控制后车辆的侧向位移下降至2.09 m，控制效果略好于单一控制，且纵向位移未明显降低，能较好保证行车的安全。经联合控制后的侧向加速度、质心侧偏角和横摆角速度的变化规律与转向控制基本一致，但此时质心侧偏角的稳定值仅为未经控制的56.7%，横摆角速度的峰值仅为未经控制的72.6%，较转向控制均更小，且此时各项运动参数均能在更短的时间内趋于稳定，能使车辆在更短的时间内趋于稳定，有效结合了制动和转向的优点。

5 结论

根据UniTire 理论搭建爆胎轮胎模型，并结合CarSim 搭建整车动力学模型进行联合仿真实验，分析直行工况下车辆的动力学响应。为保持爆胎车辆的稳定性，搭建了外环轨迹控制—内环差动制动控制联合控制策略，并通过仿真验证了所设计的控制策略的有效性。

（1）在直行工况下，车辆向爆胎轮胎一侧偏离正常行驶轨迹，且转向前轮爆胎的偏移量远大于后轮爆胎，且前轮爆胎较后轮爆胎车辆的运动状态更不稳定。

（2）爆胎车辆各运动参数变化的剧烈程度大都随车速的增加和载重的减少而增加，但车速越高，横摆角速度变化越小。此外，载重越大，爆胎后期车辆各运动参数愈发不稳定。

（3）在直线行驶时，单一控制已能对车辆偏航进行有效控制，但制动控制不能保证与后车的纵向安全距离，转向控制不能较好保证车辆的稳定性，而联合控制有效地结合了两种控制的优点，对车辆进行了有效的控制。