在ADAMS 中的动力稳定装置模型过约束研究

王炯力，王立华，陈佳明，宿晓航

（650500 云南省 昆明市 昆明理工大学 机电工程学院）

0 引言

研究多体动力学问题时，通常使用ADAMS 动力学仿真软件对模型进行仿真计算。为达到仿真计算结果准确、仿真时间缩短的目的，需要正确建立机构模型并正确添加运动约束。然而在实际机构设计中，由于虚约束的存在，ADAMS 在验证模型时会提示模型存在过约束。ADAMS 仿真时软件会自动解除其中一些冗余约束，但当模型复杂度增大、计算量增加时，冗余约束过多会导致模型仿真计算时间过长，甚至模型被“锁死”（locked up），导致仿真计算失败。关于机械结构过约束问题，郭盛[1]等研究了过约束机构的运动解析方法；韩博[2]等探究了过约束剪铰式双层周边桁架机构的组合条件并给出其运动形式；李永泉[3]等给出了一种空间被动过约束并联机构的动力学建模方法；徐晓辉[4]等探究了理想简单机械模型在ADAMS 软件中过约束问题的解决方法。然而，对于运用ADAMS 软件对实际复杂模型进行仿真时因过约束导致仿真失败的问题研究较少。针对上述问题，本文对动力稳定装置在ADAMS 中进行动力学仿真分析时冗余约束产生的原因及减少冗余约束的方法进行研究。

1 动力稳定装置的机构分析

1.1 动力稳定装置

在道路施工中，新建有砟轨道和大修有砟轨道的道床稳定性差，横向阻力减小，利用动力稳定车进行稳定作业，可以快速增加道床的稳定性和横向阻力[5]。动力稳定装置是动力稳定车的主要工作部件，在动力稳定装置作业下，松散的道床能够快速被修整，迅速提高稳定性。动力稳定装置主要由垂直下压油缸、激振器、走行轮、夹钳轮及各类油缸组成[6]，如图1 所示。稳定装置作业时，通过夹钳油缸与水平油缸共同施加压力，走行轮和夹钳轮一起夹紧钢轨。垂直油缸向下施加一定的下压力，激振器运行产生水平激振力，使道砟颗粒互相填充，密实度提高，道床稳定性增强[7]。

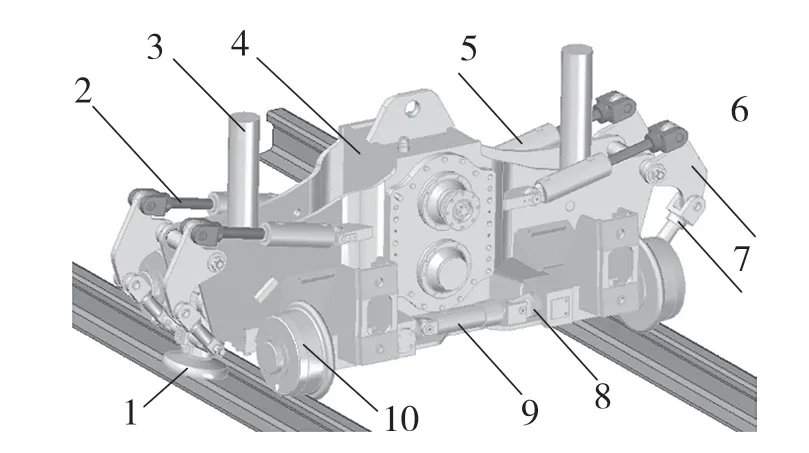
图1 动力稳定装置Fig.1 Dynamic stabilization device

1.2 动力稳定装置机构简化

要分析机械机构的动力学性能，一般应首先分析机器系统由哪些机构组成、组成机构的构件与运动副，确定各运动副之间的相对位置，并绘制出机构的运动简图[8]。其次，为更好地研究机构动力学，便于在ADAMS 软件中建模，在绘制的机构运动简图中，可以进行高副低代，计算机构的自由度确定运动件。最后，采用图解法或解析法分析其动力学[9]。

根据功能，可以将稳定装置分为夹持机构与走行机构。夹持机构包含稳定装置主体、夹钳油缸、夹钳油缸传动臂、连杆、夹持臂、夹钳轮。走行机构包含稳定装置主体、水平油缸、左右车轴、走行轮[10]。

稳定装置的工作方式决定了稳定装置的机构可以分解为3 个独立的平面机构，可以利用平面自由度计算方法分别计算其独立机构的自由度[11]：

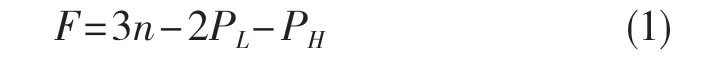
1.2.1 夹持机构车轴部分简化（俯视图）

将稳定装置的相对固定构件视为一个整体构件，得到稳定装置的夹持机构车轴部分简化图（俯视），如图2 所示。由图2 可知，稳定装置的前后端完全对称布置，其约束了稳定装置的一个旋转自由度。在横向振动时前后轴可视为虚约束，在计算平面自由度时需要去除其中一个轴的约束。

图2 夹持机构车轴部分简化图（俯视）Fig.2 S implified drawing of axle part of clamping mechanism (top view)

在移除虚约束m3、s3 和s4 后，稳定装置的夹持机构车轴部分共有2 个活动构件m1 和m2；2 个移动副s1 和s2。且根据实际情况，机构被钢轨与走行轮约束了一个旋转自由度，根据式（1），夹持机构有1 个横向平动自由度。

1.2.2 夹持机构夹钳轮部分简化（主视图）

由上文结果可得，稳定装置在横向振动方向上有一个平动自由度，因此在夹持机构夹钳轮部分简化图中将俯视机构整体简化为一个移动副s3。夹持机构夹钳轮部分简化图如图3 所示。由图3 可知，机构共有9 个活动构件m1-m9，10 个转动副r1-r10，3 个移动副s1-s3。根据式（1），计算得到夹持机构有1 个横向平动自由度。

图3 夹持机构夹钳轮部分简化图（主视）Fig.3 Simplified drawing of clamping wheel of clamping mechanism (front view)

考虑稳定装置工作实际情况，在构件m1 上沿稳定装置振动方向施加横向激振力，机构即有确定的沿振动方向平移振动的运动方式。

1.2.3 走行机构简化（侧视图）

走行机构简化图（侧视）如图4 所示，有3 个活动构件m1-m3；2 个转动副r1、r2；两个轮轨接触高副h1、h2，因此走行机构有1 个垂直于行进方向的平动自由度，2 个车轮的转动自由度，共3个自由度。

图4 走行机构简化图（侧视）Fig.4 Simplified diagram of running mechanism (side view)

根据实际情况，考虑到当在两个车轮m2、m3上施加旋转驱动，并在构件m1 上施加垂直下压力，机构失去了两个转动自由度与垂直于行进方向的平动自由度，机构拥有了确定的运动状态，即沿稳定装置行进方向平动。

通过对稳定装置简化机构的自由度进行分析计算，综合考虑各个平面上的平面机构自由度，可以看到机构的运动方式为沿钢轨方向行进的同时在垂直于钢轨的方向上反复振动，符合稳定装置的实际工作情况，机构简化合理。

2 ADAMS 中动力稳定装置的约束施加

ADAMS 中的运动副在现实中可以找到对应的实物连接，约束的自由度较多，而基本运动约束在现实中没有对应的实物连接，约束的自由度较少。

在建立模型计算时，某些在实际机构中为了增加机械强度和运动精度的约束被视为过约束；或机械结构中出现了运动副首末相连构成封闭系统成为一个闭环运动链的闭环机构[12]，这些情况在ADAMS 软件中仿真计算时均会影响整体自由度的计算，导致过约束情况发生。

事实上，运动副的本质即为基本运动约束的组合，因此在施加运动副时，考虑到机构的实际运动情况，某些机构间的连接节点不需要使用运动副连接，当进行复杂机械机构的动力学仿真时，可以使用基本运动约束以及基本运动约束组合来代替运动副，或将某些相对静止的构件使用布尔运算替代固定副连接为一个整体。在不影响机构的运动方式的前提下，减少总体的构件数的同时释放更多被约束的自由度，以达到削减被约束自由度数量的目的，减少约束方程，消除机械机构的过约束情况。

根据动力稳定装置的作业运动模式，确定各构件间的约束关系以及力和驱动约束，见表1。使用三维建模软件Solid Edge 建立动力稳定装置的三维模型，将其保存为Parasolid 文档（.x_t）格式，再导入到ADAMS 中添加运动副约束，如图5 所示。完成动力稳定装置仿真分析模型的创建，实现对动力稳定装置的道床稳定作业的仿真运动。

图5 动力稳定装置的约束施加Fig.5 Constraints on stabilization device

表1 动力稳定装置的运动副、力与驱动约束Tab.1 Kinematic pair,force and driving constraint of stabilization device

3 动力稳定装置的约束替代

3.1 稳定装置空间自由度计算

使用空间机构自由度计算方法对稳定装置模型的自由度进行计算，整个稳定装置有33 个活动构件，32 个转动副，8 个移动副，2 个固定副，4个旋转驱动。使用空间自由度计算方法计算机构的空间自由度：

式中：n——活动构件数；i——被运动副约束的自由度数，i=1，2，3，4，5；Pi——约束i个自由度的运动副数。

由式（2）得稳定装置空间自由度为-14。根据式（3），由空间自由度F及驱动数x可得机构的Gruebler 数（近似自由度）为-18：

如表2 所示，在ADAMS 中对模型进行验证，稳定装置模型有-18Gruebler 数，符合计算结果。

表2 ADAMS 软件验证结果Tab.2 Validation result in ADAMS

通过计算稳定装置模型的总体空间自由度与1.2 节的计算结果对比发现，在ADAMS 中，所有机构全部按照空间机构计算其自由度。即使机构与运动副设置符合实际运动规律，ADAMS 仍会提示自由度≤0，机构不能正常运动。ADAMS 软件在进行仿真计算时会自动解除某一些过约束[4]，使仿真计算得以进行。

3.2 基本运动约束替代运动副

进行仿真计算时若模型复杂，计算量较大，则ADAMS 会在仿真计算进行矩阵迭代时随机性报错，提示机构被“锁死”（locked up），导致仿真失败。

因此，需要使用ADAMS 软件中提供的基本运动约束替代一些运动副，并且将一些实际不会与产生相对运动的构件进行布尔联合运算，使之成为一个整体，以减小仿真计算的运算量，并释放一些不需要被约束的自由度，使机构的总体自由度≥0，消除过约束方程。

如图6 所示，针对此动力稳定装置模型，对右前、右后车轴分别与对应的右前、右后走行轮进行布尔联合运算操作，且对右侧两车轴与动力稳定装置主体使用布尔联合运算以消除固定副。以共线约束替代夹钳油缸套筒与动力稳定装置主体之间的转动副，同时替代夹钳传动臂与动力稳定装置主体之间的转动副，释放了多余的约束。

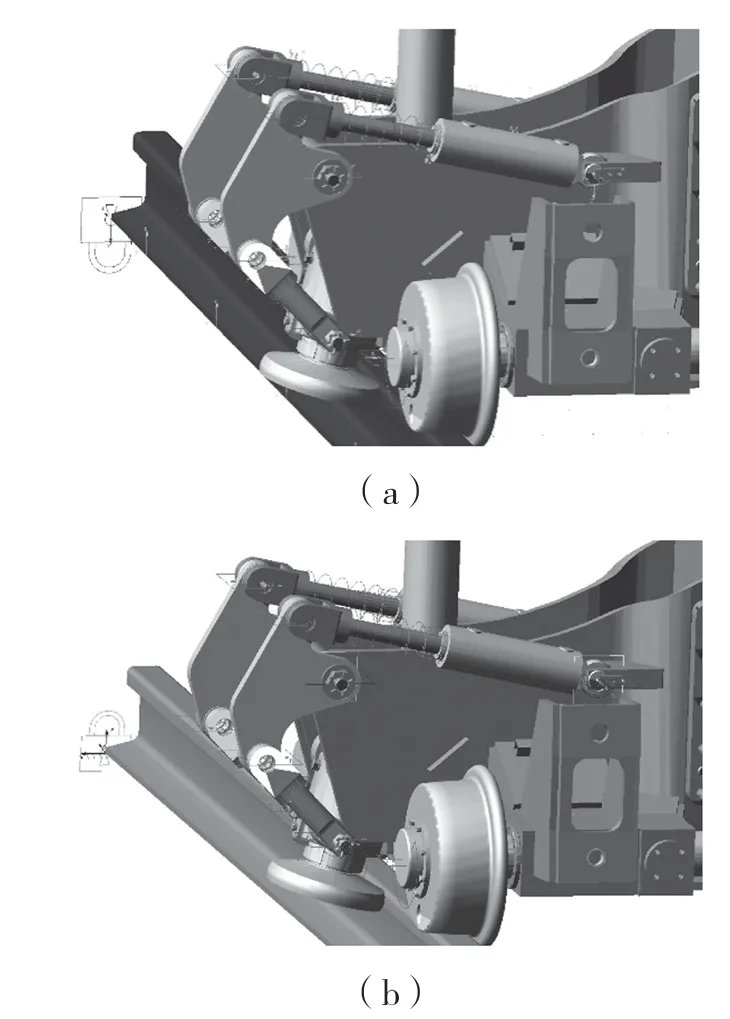
图6 基本运动约束替代运动副（局部图）Fig.6 Basic motion constraints replacing kinematic pairs (Partial graph)

修改后的模型共有29 个活动构件，20 个转动副，6 个移动副，8 个共线约束，4 个旋转驱动，2个固定副。根据空间自由度计算方法对修改后的模型计算总体Gruebler 数为12。

值得注意的是，ADAMS 软件验证结果显示有12 个Grubler 数，此近似自由度数不仅指机构外部的振动与平动，还包括机构内部的运动自由度，如表3 所示。

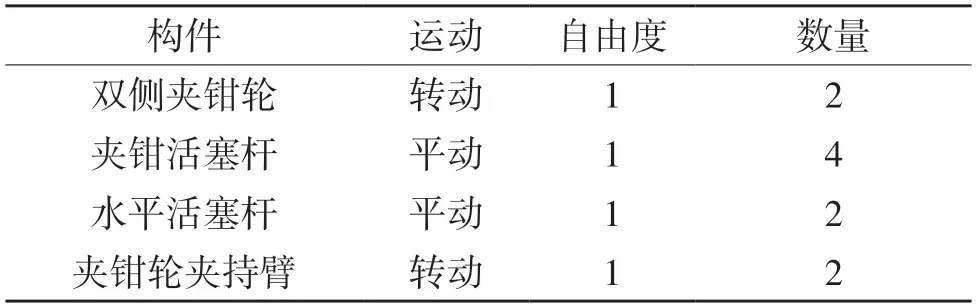
表3 机构内部自由度Tab.3 DOF in mechanism

去除机构内部自由度后，根据式(3)得到机构的外部Gruebler 数为2。

考虑到稳定装置模型的走行轮与钢轨之间的接触力限制了稳定装置的转动自由度，最后稳定装置模型的外部运动状态为沿钢轨方向行进与垂直钢轨方向振动，符合实际的稳定装置运动方式。

经过仿真计算验证，修改后的动力稳定装置模型可以进行符合预期的运动且能够正常进行动力学分析。修改后的模型总体有12 个Gruebler 数，符合机构总体自由度＞0 的条件，机构可以自由运动，同时消除了过约束方程，解决了ADAMS 软件在进行仿真计算时提示机构“锁死”的问题。

4 结论

本文针对动力稳定装置的过约束问题从机械原理的机构自由度计算入手，得到了动力稳定装置的自由度，通过对比计算得到了ADAMS 在计算机构自由度时针对所有机构均使用空间自由度计算方法的结果。并探究了使用ADAMS 中的基本运动约束替代运动副，释放多余约束以消除机构总体过约束方程的可能。本文的探究结果可以给使用ADAMS 的研究者提供一些建模及约束施加的参考。