船用921A钢高温、高应变率下动态本构模型研究

吴海军， 王可慧， 李 明， 段 建， 周 刚， 张庆明

(1. 北京理工大学 爆炸科学与技术国家重点实验室，北京 100081;2. 西北核技术研究所，西安 710024)

921A钢是我国自主研制成功的舰船用钢，与美国HY系列高强度低合金钢HY-80属同一级别，具有良好的强韧性、工艺性以及耐海水腐蚀性，是我国重要的舰船结构钢[1-2]。实战中舰船面临的主要威胁来自于反舰导弹，战斗部撞击、贯穿舰船结构钢板的过程是一个非线性瞬态动力学问题，材料通常处于大变形、高温、高应变率状态。众所周知，金属材料在动态载荷作用下的力学性能与静态时有较大差别，热软化效应也不容忽视[3]。

为了给舰船在动态载荷下的安全设计提供依据，许多学者对921A钢的动态力学行为进行了研究。刘瑞堂等[4]对907A、921A[5]及945[6-7]舰船用钢的动态断裂韧性进行了试验测试，首次获得了相关材料的动态断裂韧性数据。于兆斌等[8]测试了921A钢在不同温度下的动态断裂韧性，发现其具有优良的低温韧性，韧-脆转变温度为-100 ℃[9]。朱锡[10]首先采用分离式Hopkinson拉杆试验对921A钢在高应变率下的动态屈服强度进行了研究，发现921A钢具有显著的应变率效应。张林等[11]通过对称碰撞研究了921钢的动态损伤与破坏行为，得到了Hugoniot屈服极限以及层裂强度。李继承等[12-13]结合试验和数值模拟对921A钢帽型试样的绝热剪切行为进行了分析。伍星星等[14]研究了921A钢在拉伸、压缩、扭转断裂过程中的应力状态变化。

近年来，研究人员对921A钢更高应变率范围和高温条件下的力学性能开展了进一步的研究。王子豪等[15]采用平板撞击试验测定了921A钢极高应变率(～105s-1)下的动态屈服强度，当应变率大于1 000 s-1时，其动态屈服强度随应变率增大而迅速增大，当应变率大于3 000 s-1时，动态屈服强度随应变率增大变化缓慢。徐磊等[16]研究发现普通钢材的高温性能规范并不适用于921A钢，将Johnson-Cook(J-C)模型中的温度项与修正的Cowper-Symonds(C-S)模型直接相乘，建立了适用于火灾爆炸的921A钢本构模型。

随着数值模拟手段应用日益广泛和深入，迫切需要能够描述921A钢在高温、高应变率作用下动态力学性能的本构模型参数。J-C模型包含了应变硬化、应变率强化和热软化三种因素对材料力学性能的影响，是模拟高速撞击下金属材料大变形问题较为理想的本构模型。本文对船用921A钢高温、高应变率下的动态力学性能进行了试验研究，拟合得到了其J-C本构模型参数，并验证了模型参数的可靠性，可为舰船结构防护设计和安全评估提供参考。

1 准静态压缩试验

准静态压缩试验采用CSS44100电子万能试验机进行，通过控制加载速率使应变率为0.001 s-1。准静态压缩试验试样为Φ5 mm×5 mm的圆柱。

电子万能试验机记录的是载荷-位移(F-Δl)曲线，采用式(1)和式(2)可得材料真实应力-应变曲线。其中：A0为试样初始横截面积；l0为初始长度；σeng，εeng为工程应力、应变；σtrue，εtrue为真实应力、应变。图1为921A钢的准静态压缩真实应力-应变曲线。

(1)

(2)

从图1中可以看出，921A钢没有明显的屈服点，准静态屈服强度约842 MPa。材料屈服后，强度随应变的增加而增大，表现出较为明显的应变硬化效应。

2 动态压缩试验

2.1 试验原理

分离式Hopkinson压杆(split Hopkinson pressure bar，SHPB)结构简单，操作简便，测量方法巧妙，加载波形易于控制，是测量高应变率(102～104s-1)材料力学性能最常用的试验装置。SHPB试验的基本原理是：将短试样置于两根压杆之间，通过子弹撞击产生入射脉冲对试样进行加载，如果压杆保持弹性状态，当入射杆中的应力脉冲到达与试样的接触面时，一部分入射脉冲被反射，在入射杆中形成反射波；另一部分则通过试样透射入透射杆中，形成透射波；粘贴在入射杆和透射杆上的应变片能够记录反射波和透射波的波形。根据一维应力波理论[17]推导可得试样的应力、应变和应变率

(3)

(4)

(5)

式中：εI，εR和εT分别为由应变片测量到的入射、反射和透射应变信号；A0，L0为试样的初始横截面积和长度；A，E，C分别为压杆的横截面积、弹性模量和弹性纵波波速。

2.2 试验装置

动态压缩试验采用西北工业大学SHPB试验系统进行，如图2所示。试验应变率约为1 000 s-1、2 000 s-1、3 000 s-1、4 000 s-1，每个应变率包括室温、300 ℃、500 ℃三个温度条件(应变率4 000 s-1时只进行了室温试验)。高温试验中为了避免加载杆过热导致的损坏及杆中温度梯度过大而影响试验的准确性，采用了同步组装技术，具体工作原理见文献[18-19]。动态压缩试验试样也为Φ5 mm×5 mm的圆柱。

2.3 试验结果及分析

图3为动态压缩试验前后的试样照片，试样发生明显的墩粗变形，呈鼓形。其中，室温、应变率3 000 s-1情况下，应变值达到了0.70，而试样未发生一般钢材常见的剪切破坏，说明921A钢在高应变率载荷作用下依然有很好的韧性，与普通高强钢相比，可以依靠较大的变形吸收更多能量。

通过SHPB试验，得到了921A钢在室温、300 ℃、500 ℃时，不同应变率下的动态压缩应力-应变曲线，如图4所示。从图4中可以看出，与室温、准静态(～10-3s-1)时的应力-应变曲线相比，921A钢表现出明显的应变率强化效应和热软化效应。室温、高应变率(～103s-1)条件下动态屈服强度较准静态屈服强度显著提高，而应变硬化效果基本消失；相同应变率(～103s-1)时，高温(300 ℃、500 ℃)条件下的屈服强度较室温时明显降低。

2.3.1 应变率效应分析

图5为不同温度下，921A钢屈服应力随应变率的变化。由图5中可以看出，虽然数据存在一定的波动，但总的趋势是屈服应力随应变率的增大而增大。室温条件下，应变率4 000 s-1时921A钢的屈服应力由准静态时的842 MPa增加至1 203 MPa(增幅约43%)，较1 000 s-1时的1 093 MPa增加也有约110 MPa(增幅约10%)。300 ℃和500 ℃条件下，应变率由1 000 s-1增大至3 000 s-1，其屈服应力变化不大。

应变率敏感性因子β[20]定量表征了应变率对应变率效应的影响，可以近似地估计为屈服应力相对于应变率对数的斜率，即

(6)

图6为不同温度下，921A钢应变率敏感因子随应变率的变化。从图中可以看出，室温时，应变率敏感因子随应变率增大而增大；高温时，应变率敏感因子明显小于室温时，且随应变率增大变化不大。即高温条件下，921A钢的应变率强化效应弱于室温条件，且对应变率的变化不敏感。

2.3.2 热软化效应分析

高温条件下，克服位错运动所需的能量较小，宏观上表现为材料的塑性增强，屈服应力降低。图7为921A钢不同应变率时屈服应力随温度变化曲线。从图7中可以看出，921A钢表现出明显的热软化效应，500 ℃时的屈服应力较室温时大幅减小，较室温时下降约400 MPa(降幅约48%)。同时可以看出，随着温度的升高，921A钢的应变率强化效应逐渐减弱，500 ℃时，应变率1 000 s-1、2 000 s-1、3 000 s-1时的屈服应力变化不大。

温度敏因子na定量表征了温度对温度效应的影响，可以近似地估计为屈服应力的自然对数相对于温度自然对数的斜率，即

(7)

式中：σ1，σ2为不同温度下的流动应力；T1，T2为相对应的温度。

图8为不同应变率下，921A钢温度敏感因子随温度的变化。从图中可以看出，相同应变率条件下，温度敏感因子基本不随温度变化；应变率2 000 s-1时的温度敏感因子明显大于应变率1 000 s-1时的温度敏感因子。即较高应变率时，921A钢的热软化效应强于较低应变率时，且对温度的变化不敏感。

3 Johnson-Cook本构模型参数拟合

(8)

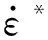
取参考应变率0.001 s-1，参考温度298 K，921A钢的熔点为1 765 K，拟合准静态和动态试验数据[22-23]，得到921A钢的J-C本构模型参数，如表1所示。

表1 921A钢的J-C本构模型参数Tab.1 The J-C constitutive model parameters of 921A steel

将921A钢的J-C模型预测曲线与试验应力-应变曲线进行对比，如图9所示。可以看出，在试验应变率和温度范围内，预测曲线与试验曲线吻合较好，初步验证了J-C模型参数的准确性。

4 动态冲击试验及数值仿真验证

无论是准静态压缩还是SHPB试验，都是一维应力应变状态的简单加载，模型对穿甲过程中靶板响应的模拟能力还有待进一步检验。为此，我们开展了弹体高速撞击双层921A钢板的试验，并采用得到的J-C本构模型参数对试验现象进行了数值仿真。

4.1 弹体撞击双层921A钢板试验

试验弹体长度为136.8 mm，直径为72 mm，质量为1.65 kg。试验靶板为双层921A钢板，厚度分别为6 mm+6 mm和8 mm+8 mm两类，截面尺寸为600 mm×600 mm，两层水平间隔600 mm，弹体前进方向与靶板法线方向成30°夹角。采用130 mm一级轻气炮作为发射平台，由于试验弹外径小于气炮口径，为次口径发射，依靠尼龙弹托进行炮膛内弹丸的定位及推力的传递，弹丸撞靶前采用撞击止退的方法进行脱壳。设计了专门的试验靶架，起到固定靶板、预置倾角的作用，靶板后箱体内密实装填木材对弹体进行软回收。为保证试验安全，靶架侧面覆盖防护钢板，后面堆放混凝土防护靶，整个靶架置于气炮试验靶箱内。

弹体撞靶速度采用激光测速系统进行测试，其原理如图13所示。预设的激光光束被飞行的弹体遮挡，测速系统通过记录遮挡激光光束形成的时间间隔来计算弹速。试验靶箱一侧开有光学窗口，采用高速摄影系统，记录弹体撞靶前飞行速度和姿态，如图14所示。弹托在与脱壳器撞击后完全碎裂，弹体保持水平方向运动，弹体与弹托碎片共同向前运动，直至撞击靶板，如图15所示。

4.2 靶板破坏仿真结果与试验结果对比

考虑到问题的对称性，建立1/2几何模型，弹、靶均采用8节点三维实体单元，在对靶板进行网格剖分时，弹靶接触区网格加密，距离弹靶接触区较远的地方逐渐稀疏，既能满足数值模拟精度的要求，又能有效控制网格数量。弹体与靶板之间采用侵蚀接触算法，对称面施加对称约束，靶板四周固支。

弹体对6 mm+6 mm双层921A钢板的撞击速度为575 m/s。表2为靶板弹孔平均直径试验和仿真结果的对比，可以看出第一层靶板弹孔平均直径的仿真值明显小于试验值，第二层靶板弹孔平均直径的仿真值与试验值吻合较好。图16为靶板破坏形貌的对比。

表2 6 mm+6 mm双层921A钢板弹孔平均直径试验与数值仿真结果Tab.2 Experimental and simulation results of average diameter of projectile holes of 6 mm+6 mm double-layer 921A steel plate

分析认为，弹体撞击第一层靶板时，靶板因环向拉伸应力而形成“星形”裂纹，在裂纹扩展、花瓣形成的过程中，大量弹托碎块随之而来，以较高的速度撞击靶板，弹托碎块的动能转化为靶板的变形能和裂纹扩展能，所以第一层靶板的塑性变形区域和裂纹扩展区域较数值仿真结果大得多。试验后在第一层靶板前发现大量弹托碎块，而第一、第二层靶板之间的弹托碎块较少，也表明了这一分析的合理性。第二层靶板受弹托碎块影响较小，所呈现的破坏模式较为典型，数值仿真结果与试验结果非常相似。图17为试验中收集到最大的一块靶板花瓣形碎块，与数值仿真结果在形状和变形特点上都基本一致。

弹体对8 mm+8 mm双层921A钢板的撞击速度为484 m/s。本发试验前采取措施对弹托碎片进行阻挡以减小其对靶板的撞击效应，因此受弹托碎块影响较小。数值仿真得到的靶板弹孔平均直径和破坏形貌与试验结果非常接近(见表3)，塑性变形区域和裂纹扩展区域基本一致，如图18所示。弹孔上方被撕裂较大碎块，在数值模拟结果中也有较好地体现，如图19所示。

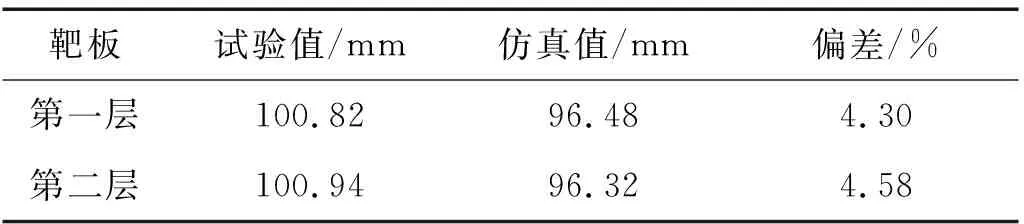
表3 8 mm+8 mm双层921A钢板弹孔平均直径试验与数值仿真结果Tab.3 Experimental and numerical simulation results of average diameter of projectile holes of 8 mm+8 mm double-layer 921A steel plates

5 结 论

本文基于准静态压缩和不同温度、不同应变率的SHPB试验结果，分析了温度、应变率对921A钢力学性能的影响，拟合得到了921A钢的J-C本构模型参数，对比弹体高速撞击双层921A钢板的动态冲击试验结果和数值仿真结果，得到的主要结论如下：

(1) 室温、准静态时，921A钢没有明显的屈服点，材料屈服后，强度随应变的增加而增大，表现出明显的应变硬化效应。

(2) 高温、高应变率时，921A钢具有明显的应变率强化效应和热软化效应，应变硬化效应基本消失；随着温度的升高，应变率强化效应逐渐减弱；热软化效应对应变率变化不敏感。

(3) 拟合得到的J-C本构模型能够反映应变、应变率和温度对921A钢动态力学性能的影响，在试验应变率和温度范围内，模型预测曲线与试验应力-应变曲线吻合较好。

(4) 采用获得的921A钢J-C本构模型参数对弹体高速撞击双层921A钢板试验进行了数值仿真，靶板弹孔平均直径和破坏形貌与试验结果吻合较好，进一步验证了模型参数能够较好地描述921A钢在高速冲击条件下的动态力学行为。