考虑支点变形和摩擦的可倾瓦轴承动力学特性研究

2022-10-27金英泽袁小阳

振动与冲击 2022年20期

金英泽，袁小阳

(1. 大连海事大学船舶与海洋工程学院，辽宁大连 116026；2. 西安交通大学现代设计及转子轴承系统教育部重点实验室，西安 710049)

可倾瓦轴承凭借优良的稳定性广泛应用于汽轮机、燃气轮机和核主泵等重大装备旋转机械。可倾瓦轴承动力学特性研究从刚度阻尼系数研究已经发展到非线性动力学特性研究[1-3]。支点是实现瓦块自适应摆动的关键结构组件，常见的支点形状主要有柱形支点和球形支点。从接触方式来看，柱形支点为线接触方式，球形支点为点接触方式；从运动形式来看，柱形支点依靠滚动，球形支点依靠滑动，后者的摩擦因数比前者要大两个数量级[4]。因此，基于刚性光滑支点假设的理想支点模型有必要发展为计入支点变形和摩擦的真实支点模型。

可倾瓦轴承支点变形的研究大多采用赫兹接触理论和有限元仿真。Kirk等[5]基于赫兹接触理论给出了典型可倾瓦轴承瓦块支点刚度和变形方程，证明了支点刚度在可倾瓦轴承动特性计算中的必要性。李萌萌等[6]采用有限元仿真分析了点支承、线支承和球支承可倾瓦轴承的支点垂直静刚度。王占朝等[7]研究了支点变形对水润滑可倾瓦推力轴承启动过程初始倾斜转速的影响，数值结果得到了试验验证。Mehdi等[8]研究了支点柔性对柱形和球形支点可倾瓦轴承静动特性的影响，证明了柔性支点模型更接近试验数据。Shi等[9]研究了柱形和球形支点可倾瓦轴承对立式和卧式转子非线性动力学特性的影响。值得一提的是：Jin等[10]利用支点变形的优势提出一种可调弹性支点可倾瓦轴承，并分析了该轴承的非线性动力学特性。

可倾瓦轴承支点摩擦的研究相对较少。Wygant等[11]试验测试了柱形和球形支点可倾瓦轴承静平衡位置和动特性系数，重点关注了支点摩擦对轴承性能的影响。Kim等[12]提出了支点摩擦模型，分析了支点摩擦对可倾瓦轴承静态和瞬态性能的影响。Kim等[13]研究了支点摩擦对可倾瓦轴承转子系统非线性响应和分岔特性的影响，表明支点摩擦对评估转子系统稳定性起重要作用。党超等[14]研究了支点摩擦对可倾瓦轴承润滑性能的影响。

在上述研究中，支点变形和摩擦的耦合作用尚未计入到支点模型中，支点设计参数对非线性动力学特性的影响规律也尚未摸清。鉴于此，本文开展考虑支点变形和摩擦的可倾瓦轴承动力学特性研究。以水润滑球形支点可倾瓦轴承为研究对象，建立考虑支点弹性力和摩擦力矩的可倾瓦轴承系统非线性动力学模型和分析方法，研究支点变形和摩擦对可倾瓦轴承动力学特性的影响，揭示支点半径比和支点摩擦因数对轴承性能的影响规律。

1 理论模型

研究对象是球形支点可倾瓦轴承，轴承含四块可倾瓦，润滑介质是水，承载方式为瓦间承载。球形支点可倾瓦轴承坐标系和瓦块支点接触示意图，如图1所示。相关符号在文中有标注。轴颈存在静载和不平衡质量，1号瓦和2号瓦为承载瓦，3号瓦和4号瓦为非承载瓦。

1.1 流体动压润滑模型

在等温、不可压缩流体假设下，含有紊流修正系数的非定常雷诺方程为

(1)

式中：R为轴颈半径；h为液膜厚度；p为液膜压力；μ为流体动力黏度；ω为转动角速度；t为时间；φ，z分别为周向和轴向坐标；kφ，kz为紊流修正系数。当kφ=kz=12时，即为经典层流雷诺方程。

假设瓦块表面是刚性的，轴颈与瓦块是平行的，则考虑支点接触变形的可倾瓦膜厚方程为

h=cp-(cp-cb-ξ)cos(β-φ)+ejcos(φ-θ)+
Rδsin(β-φ)

(2)

式中：cp为瓦块径向间隙；cb为轴承径向间隙；ξ为瓦块径向位移；β为支点位置角；ej为轴颈偏心距；θ为轴颈偏位角；δ为瓦块摆角

当瓦块径向位移大于零时，支点发生接触变形且变形量等于瓦块位移量；否则，瓦块与支点不发生接触。因此，支点变形ξp和瓦块位移ξ的关系可描述为

(3)

适用于滑动轴承设计的紊流润滑理论主要有三个[15]：Constantinescu理论、Ng、Pan和Elrod理论以及Hirs理论。采用精度较好、应用较多的Ng和Pan紊流模型确定紊流修正系数

(4)

式中，Re可称之为有效雷诺数，它的表征取决于流态的性质。一般认为，流体中可能存在三种流态，分别是层流、紊流和过渡流态。滑动轴承的流态可根据局部雷诺数和临界雷诺数的对比来确定，本文采用的两个临界雷诺数分别是800和1 500[16]，则有

(5)

式中：Rel为局部雷诺数，Rel=ρωRh/μ；ρ为流体密度；c1-4为待定系数，通过Re及其一阶导数在临界雷诺数处连续确定。

可倾瓦轴承非线性液膜力分量fx和fy、瓦块径向液膜力fr和瓦块液膜力矩Mp的表达式为

(6)

(7)

(8)

式中：i为瓦块序号；L为轴承长度；φin，φout分别为进、出液边位置角。

1.2 瓦块-支点接触模型

赫兹接触理论[17]的基本假设为：①接触变形很小且在弹性极限范围内；②接触体可视为弹性半空间；③接触表面连续且非共形；④接触表面无摩擦。则支点弹性力可表达为支点变形的非线性幂函数

(9)

式中，K为广义接触刚度，其值取决于材料属性和接触表面形状。球形支点与瓦背球窝的接触属于凸球与凹球的接触问题，广义接触刚度可表达为

(10)

式中：Rs为瓦背球窝半径；Rp为支点半径；σs和σp为材料参数，由式(11)给出

(11)

式中：υk为泊松比；Ek为弹性模量。

库伦摩擦定律的基本假设为：①滑动摩擦力与接触表面的正压力成正比，跟接触面积无关；②滑动摩擦力与滑动速度大小无关。另假设接触表面间的动摩擦因数与静摩擦因数相等且为常数值，则支点对瓦块的滑动摩擦力Ff和摩擦力矩Mf可表达为

(12)

式中，μf为支点摩擦因数。

如果瓦块处于摆动状态，则瓦块受到滑动摩擦力矩的作用，摩擦力矩方向与瓦块摆动方向相反；如果瓦块处于静止状态，则摩擦力矩取决于液膜力矩和最大静摩擦力矩的大小，摩擦力矩方向与液膜力矩方向相反。综上所述，支点对瓦块的摩擦力矩可表达为

(13)

式中，“·”为一阶导数d/dt。

1.3 可倾瓦轴承非线性动力学模型

球形支点可倾瓦轴承瓦块存在多个方向的自由度。本文采用的是瓦块主摆动方向和径向方向自由度的点支承建模方法，假设瓦块不发生其他方向的摆动。考虑支点变形和摩擦后，可倾瓦轴承在不平衡谐波与静载联合激励下的动力学方程可描述为

(14)

式中：mj为轴颈质量；xj，yj为轴颈位移分量；“··”为二阶导数d2/dt2；eu为不平衡偏心距；Wy为轴承静载；Ip为瓦块转动惯量；mp为瓦块质量。

假设瓦块厚度是均匀的，则瓦块转动惯量和瓦块质量的表达式推导为

(15)

(16)

式中：ρp为瓦块密度；α为瓦块包角；hp为瓦块厚度；ζ为支点系数，即瓦块入口边到支点的包角与瓦块包角的比值。该表达式计算结果与SolidWorks软件计算结果基本一致。

2 计算方法

采用有限差分法求解雷诺方程(见式(1))，采用半步长五点中心差商近似取代雷诺方程中的偏导数，将方程化为一组代数方程，为加速收敛，采用超松弛迭代法求解方程组得到压力分布。迭代过程纳入了雷诺边界条件，见式(17)。采用经典显式欧拉法逐步求解可倾瓦轴承动力学方程(见式(14))。为了兼顾计算精度和计算效率，数值方法的参数设置如下：松弛因子为1.7，单瓦液膜在周向和轴向的网格数量为20×14，压力收敛精度为10-6，轴颈和瓦块初始位置和速度皆为0，时间步长为10-6s。

(17)

需要说明的是：由于球形支点计入了摩擦力矩作用，在逐步计算的过程中，当相邻两个时刻的瓦块摆速符号相反时，表明在该段时间内必然存在摆速为0的时刻，即瓦块停止摆动，但数值计算忽略了这个状态，造成瓦块始终受到滑动摩擦力矩的作用，而忽略了静摩擦力矩的作用，这是不符合物理意义的。本文采用的处理方式是：当相邻两时刻的瓦块摆速符号相反时，令后一时刻的瓦块摆速为0，这样可以确保数值计算的可靠性和稳定性。

3 计算结果与讨论

计算案例采用的球形支点可倾瓦轴承结构和运行参数，如表1所示。其中，支点半径比指的是支点半径与瓦背球窝半径的比值，它是重要的支点设计参数。0～400 μm的不平衡偏心距可以激发0～88.8 kN的动态载荷，由于静载为44.4 kN，因此案例涵盖动载小于静载、动载等于静载和动载大于静载时的运行工况。

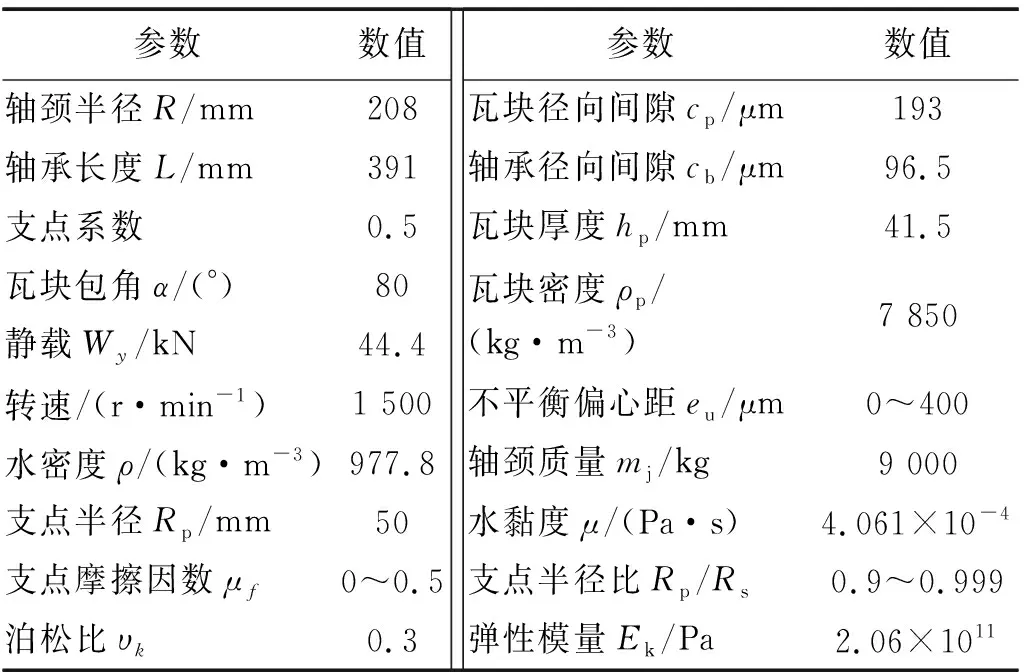
表1 可倾瓦轴承参数Tab.1 Parameters of tilting-pad journal bearing

3.1 考虑支点变形和摩擦的可倾瓦轴承动力学分析

本部分计算采用的支点半径比为0.995，支点摩擦因数为0.1。多种不平衡偏心距下支点变形和支点摩擦力矩的响应曲线，如图2所示。从图2可知，不平衡偏心距对二者可产生较大影响。当不平衡偏心距为0时，支点变形和摩擦力矩随时间最终达到一个恒定值，此时支点变形为20.8 μm，支点摩擦力矩为-226 N·m。在不平衡谐波激励下，支点变形和摩擦力矩随时间呈周期性波动，不平衡偏心距越大，波动幅度越大。当不平衡偏心距为400 μm时，最大支点变形为47.3 μm，最大支点摩擦力矩为776 N·m。

针对三种典型不平衡偏心距研究了支点变形和摩擦对轴心轨迹的影响，如图3所示。支点变形可使轴承间隙增大，这会导致轴承刚度和承载力降低，因此考虑支点变形后，静态轴颈偏心距和轴心轨迹幅值皆增大。支点摩擦抑制了瓦块摆动的自适应性，导致瓦块液膜合力不再通过支点，轴承存在交叉刚度，因此考虑支点摩擦后，静态轴颈偏位角不再为0，轴颈偏心距增大，轴心轨迹幅值减小。以100 μm不平衡偏心距为例，仅考虑支点变形时，轴心轨迹幅值增大58%；仅考虑支点摩擦时，轴心轨迹幅值减小22%；综合考虑支点变形和摩擦时，轴心轨迹幅值增大40%。结果表明，支点变形相比支点摩擦对轴心轨迹的影响程度要更大一些。

图4研究了支点变形和摩擦对瓦块摆角响应的影响(eu=100 μm)。支点变形可增大瓦块摆幅，支点摩擦可减小瓦块摆幅，这与其对轴心轨迹幅值的影响是相似的。以2号承载瓦为例，仅考虑支点变形时，瓦块摆幅增大101%；仅考虑支点摩擦时，瓦块摆幅减小93%；综合考虑支点变形和摩擦时，瓦块摆幅减小5%。由此可见支点摩擦相比于支点变形对瓦块摆角响应的影响更大一些。考虑支点摩擦下的瓦块摆角响应特征在于最大摆角在一段时间内保持不变，这是因为此时瓦块动态液膜力矩小于最大支点静摩擦力矩，典型特征如图4(c)，非承载瓦的摆角不再随时间发生变化，此时瓦块不摆动，其最终摆角由摆动历程所决定。

图5针对多种不平衡偏心距研究了支点变形和摩擦对轴承最小液膜厚度的影响。从图5可知，支点变形可使轴承最小液膜厚度增大，增幅可达10%，这是因为轴承间隙有所增大。支点摩擦对轴承最小液膜厚度的影响与不平衡偏心距大小有关，但影响较小。当不平衡偏心距较小时(0～100 μm)，支点摩擦可使轴承最小液膜厚度减小，减幅不超过4%；当不平衡偏心距较大时(150～400 μm)，支点摩擦可使轴承最小液膜厚度增大，增幅不超过3%。支点变形和摩擦的综合作用可使轴承最小液膜厚度增大，增幅可达7%。

3.2 支点半径比对可倾瓦轴承动力学特性的影响

本部分计算采用的不平衡偏心距为200 μm，支点摩擦因数为0.1。图6研究了支点半径比对轴心轨迹的影响。轴心轨迹的形状与拐点受支点半径比的影响较大，支点半径比越小，轴心轨迹相对越复杂。轴心轨迹幅值随支点半径比的增大而减小，这是因为支点半径比的增大可使支点刚度增大，进而使轴承刚度增大。当支点半径比从0.9增大到0.999时，轴心轨迹幅值从69.6 μm减小到32.1 μm，减幅达54%。结果表明，将支点半径比设计得大些有利于抑制轴颈振动。

图7研究了支点半径比对瓦块振动响应的影响。瓦块振幅随支点半径比的增大而减小，支点半径比越大，支点摩擦效应也更加明显，体现在瓦块在最大摆角处停滞的时间更长。当支点半径比从0.9增大到0.999 时，瓦块摆动振幅从0.014 6°减小到0.0041 3°，减幅达72%；瓦块径向振幅从41.4 μm减小到6.48 μm，减幅达84%。结果表明，适当增大支点半径比有利于抑制瓦块振动。

图8研究了支点半径比对瓦块最小液膜厚度的影响。可以看出，相比于2号瓦，1号瓦的最小液膜厚度更小，这是支点摩擦效应导致的。也就是说，可倾瓦轴承的最小液膜厚度发生在1号瓦上。当支点半径比在0.96～0.97时，轴承最小液膜厚度有最大值，约为44.2 μm。从提高轴承承载能力来看，宜将支点半径比设计在该范围内。

3.3 支点摩擦因数对可倾瓦轴承动力学特性的影响

本部分计算采用的不平衡偏心距为200 μm，支点半径比为0.995。图9研究了支点摩擦因数对轴心轨迹的影响。轴心轨迹幅值随支点摩擦因数的增大而减小，这是因为支点摩擦因数的增大导致轴承交叉刚度有所增大。当支点摩擦因数从0增大到0.5时，轴心轨迹幅值从42.4 μm减小到33.9 μm，减幅达20%。结果表明，适当增大支点摩擦因数有利于抑制轴颈振动。

图10研究了支点摩擦因数对瓦块振动响应的影响。瓦块摆动振幅和瓦块径向振幅随支点摩擦因数的增大呈现不同程度的减小，前者减幅显著，后者减幅较小。当支点摩擦因数从0增大到0.5时，瓦块摆动振幅从0.008 35°减小到0，减幅为100%；瓦块径向振幅从11.7 μm减小到11.0 μm，减幅为6%。支点摩擦因数的增大可使摩擦力矩增大，从而阻碍了瓦块的摆动。当支点摩擦因数达到0.5时，瓦块动态液膜力矩恒小于最大支点静摩擦力矩，导致瓦块不摆动，此时瓦块最终摆角取决于瓦块的摆动历程。

图11研究了支点摩擦因数对瓦块最小液膜厚度的影响。当支点摩擦因数为0时(光滑支点)，两个承载瓦的最小液膜厚度相等；当支点摩擦因数非0时，1号瓦的最小液膜厚度更小，轴承最小液膜厚度发生在该瓦上。轴承最小液膜厚度随支点摩擦因数的增大呈先略增后减小的趋势，支点摩擦因数为0.1可使轴承最小液膜厚度有最大值43.2 μm。结果表明，支点摩擦因数控制在0～0.15内可使轴承具有较高的承载能力，支点摩擦因数过大会导致轴承承载能力大幅下降。