行星齿轮机电耦合动力学及其电参数影响机理研究

2022-10-27肖正明刘佳伟谭加林郑胜予

振动与冲击 2022年20期

肖正明，刘佳伟，谭加林，郑胜予

(昆明理工大学机电工程学院，昆明 650500)

以电机为动力源拖动齿轮传动系统，是一种典型的机电耦合系统，被广泛应用于电动汽车、风力发电机、数控车床等多种机械装备。随着电机拖动齿轮系统向大功率、集成化、高功率密度等方向发展，机电耦合作用引起的机械振动问题越发明显，传统只关注于电机或机械传动系统的动力学模型，无法对此状况下的系统动态响应进行精准预测。因此，有必要考虑机电耦合关系，建立电机-齿轮机电耦合系统才能得出更为真实的系统动态特性，对于电机-齿轮系统动力学设计及状态监测具有重要意义。

目前针对电机-齿轮系统机电耦合动力学问题，已有广泛的研究。Khabou等[1]考虑了电机扭矩变化对齿轮激励，用Newmark法计算了定轴齿轮动力学响应。Girsang等[2]在不同的风和电网条件下进行风力发电机与行星齿轮减速器动力学仿真，得出了系统的瞬态响应。Chen等[3]根据机电系统扭振响应提出了对电机控制策略的改进，从而减小电机的振动。Bai等[4]研究表明机电耦合效应会加剧齿轮的振动。刘长钊等[5]提出了一种可用于分析变速过程的“电机-齿轮传动系统-滚筒”的纯扭转动力学模型。霍军周等[6]分析了电机转矩主从控制和转速跟随控制两种控制方式，对齿轮传动系统振动响应的影响。于蓬等[7]将减速器和电机整体考虑，基于Maxwell电磁理论得出电磁转矩激励，能更好地反映机电耦合系统的振动噪声特性，并通过试验验证了该模型。易园园等[8]面向电机启动、冲击载荷等非稳态工况，揭示了电机-多级齿轮系统的扭振信号与定子电流信号的关系。赵心颖等[9]将电气振荡转化为作用在机械系统的动态激励，得出了电气控制参数对传动系统振动的影响关系。朱海燕等[10]对比有、无电磁力矩谐波分量激励的齿轮箱动力学响应，研究齿轮箱体和电机的振动特性。

综上所述，大多数研究将电机-齿轮系统动力学模型简化为纯扭转模型，忽略了时变轴承刚度激励影响，并且主要关注于电气系统对传动系统的激励作用，较少关注传动系统振动如何影响电机系统电气参数变化。本文从动力学角度出发，将时变啮合、轴承刚度激励转化为关于转角的函数，建立了可适用于不同转速工况的电机-齿轮机电耦合动力学模型。通过分析系统振动响应及电机定子电流的频谱对应关系，揭示了传动系统齿轮、轴承刚度激励对电机定子电流的调制规律。为进一步电机-齿轮机电耦合系统的动力学设计及状态监测提供了理论基础。

1 电机-齿轮系统机电耦合动力学模型

1.1 行星齿轮传动系统集中参数模型

行星齿轮传动系统平移-扭转集中参数模型，如图1所示。在图1中，设置有三种类型坐标系用于描述行星齿轮系统：大地坐标系OXY，固定在行星架上并随其转动的动坐标系oxy，固定在行星轮上的动坐标系opnxpnypn，n=1,2,…,N，N为行星轮个数，其中opnxpnypn坐标轴轴线与oxy坐标轴轴线相平行。每个元件有x，y，θ三个方向自由度，θc为行星架在大地坐标系OXY中的转角，θs及θr分别为太阳轮、内齿圈在动系oxy中的转角，θpn为行星轮在动系opnxpnypn中的转角。Ts为作用在太阳轮的驱动力矩，Tc为作用在行星架上的负载力矩。φn为第n个行星轮在oxy中的位置角，φn=2π (n-1)/N。

在动坐标系oxy中行星轮系可视为定轴轮系，由此可确定齿轮啮合变形δspn及δrpn

(1)

式中，espn(θpn)及erpn(θpn)分别为太阳轮-行星轮、行星轮-内齿圈之间的齿轮综合啮合误差，可写为以行星轮转角为自变量的正弦函数，其幅值由齿轮加工精度决定。

进一步，考虑时变啮合刚度影响，并将啮合阻尼视为定值[11]，可计算出动态啮合力为

(2)

考虑构件切向加速度引起影响，应用非惯性系的牛顿定律[12]建立行星齿轮传动平移-扭转动力学方程。太阳轮、内齿圈、第n个行星轮(n=1,2,3)及行星架的运动微分方程依次如式(3)～式(6)所示

(3)

(4)

(5)

(6)

式中，δpnx，δpny，δpnt分别为行星轮与行星架在x，y及切向方向的相对位移，可由坐标系oxy与坐标系opnxpnypn的位置关系计算得出

(7)

1.2 电机-齿轮系统机电耦合模型

在dq坐标系中建立异步电机动态模型：使用Park变换将电机定子三相电压转化到两相旋转dq坐标系中，异步电机电气参数也折算到dq轴等效电路模型中，对应的Park变换公式、电压方程、磁链方程和电磁力矩方程如式(8)～式(11)所示[13]

(8)

(9)

(10)

Te=1.5ne(ΨdsIqs-ΨqsIds)

(11)

式中：下标d，q分别为d，q轴上分量；下标s，r分别为电机定子、转子；U，I，R，L，Ψ分别为电压、电流、电阻、自感、漏感及磁链；Lm为定转子互感；ne为电机磁极对数；ω为dq坐标系角速度；ωr为电机电角速度，ωr=neωM，ωM为电机转子角速度。

如图2所示，电机转子轴与太阳轮相连，行星架轴与负载转子相连。在大地坐标系OXY中太阳轮转角为(θc+θs)，由此电机转子及负载端动力学方程为

(12)

以电机与行星齿轮系统的力学关系，建立机械系统与电气系统的联系，结合式(3)～式(12)可建立电机-齿轮系统机电耦合动力学方程为

(13)

式中：X为广义自由度；M，C，G，K，Kt，Ka，T，E分别为广义质量矩阵、总体阻尼矩阵、陀螺矩阵、总体刚度矩阵、向心刚度矩阵、切向刚度矩阵、外部激励力矩向量及啮合误差激励向量；U，R，I，Ψ，ω，L分别为电压向量、电阻矩阵、电流向量、磁链向量、角速度矩阵及电感矩阵。

建立了包含力-电-磁三种物理方程的动力学模型，如式(13)所示。第一个方程是多自由度受迫振动的力学方程，其在内部受齿轮时变啮合刚度与啮合误差激励，在外部受由电磁力矩Te及负载TL激励；第二个方程代表电机等效电路模型，其由电机电气控制系统及转子转速共同决定；第三个方程用于计算动态磁链；第四个方程用于计算动态电磁力矩。由此建立了电机-齿轮系统机电耦合模型。

2 时变刚度求解

2.1 时变啮合刚度求解

本文使用文献[14]提出的改进能量法计算时变啮合刚度，该方法考虑了较为真实的过渡曲线方程，提高了啮合刚度的计算精度。行星齿轮系统主要参数如表1所示。

表1 行星齿轮传动系统主要参数Tab.1 The main parameters of the planetary gear

受电气控制系统影响，传动系统转速具有时变性，使用角度表示时变啮合刚度，比时间表示更具优势。采用角度表示时变刚度之后，不需要系统转速信息，使得模型在不同转速工况或非稳态工况也具有适用性。进一步，将时变啮合刚度展开傅里叶级数形式，如式(14)所示

(14)

式中：a，b为傅里叶级数各项系数；l为谐波次数；γn为啮合初相位；γr为内啮合相位差，其取值与行星轮齿数有关，齿数为奇数时取为0，齿数为偶数时取为π。

在保证计算精度的情况下为减少计算量，使用8阶傅里叶级数拟合由改进能量法得出的时变啮合刚度。太阳轮-行星齿轮1时变啮合刚度kspl计算结果及级数拟合对比如图3所示。8阶傅里叶级数各项系数如表2所示。

表2 傅里叶级数各项系数Tab.2 The Fourier series coefficients

2.2 太阳轮处时变轴承刚度求解

基于赫兹接触理论建立轴承分析模型计算时变轴承支承刚度[15]，轴承分析模型如图4所示。为简化计算，模型假设轴与内圈无相对滑动，外圈与箱体刚性连接，滚子与滚道之间不发生相对滑动，不计轴与内圈之间的游隙，在运动期间滚子始终为等距排列，滚子只在受到压缩时才产生变形。在该假设下，轴承的变形主要由滚子与轴承内外圈之间的接触变形组成。

第i个滚子的接触变形可以表示为

(15)

式中：xb，yb分别为轴承内圈圆心在x，y向的位移，即为内圈与外圈在的相对位移；φi为轴承滚子位置角；Nb为轴承滚子个数；θz为轴承内圈的转角。

滚子形状为球形，根据赫兹接触理论，由接触变形产生的动态轴承力为

(16)

式中：Kc为赫兹接触刚度，由轴承材料、接触形状决定；H(δbi)为海维赛德函数用于判断滚子i是否发生接触变形，当δbi为正时为1，否则为0。

为充分考虑振动响应对动态轴承力的影响，并与行星齿轮动力学模型直接地联系起来，将轴承力转化为轴承刚度计算，轴承支承刚度定义为

(17)

通常支承刚度矩阵主对角元素远远大于非对角元素，可将非对角元素忽略[16]，轴承在xb，yb方向上的支承刚度可表示为

(18)

在稳定工况下，振动位移对轴承滚子接触变形影响较小，xb，yb取为定值，太阳轮轴承内外圈的直径分别为40 mm和80 mm，滚子数目9，滚子赫兹接触刚度Kc为4.2×108N/m，利用式(18)可计算出其时变轴承刚度。在稳定工况下太阳轮x方向轴承支承刚度变化如图5所示。

3 传动系统振动-电机电流作用关系

在式(12)中电机轴变形产生的力为作用在电机转子上的负载记为Td。受齿轮系统以及负载波动等动态激励，假设Td波动频率为fd，受Td激励下电机转子角速度、电磁力矩动态响应可写为

(19)

在dq坐标系中，定义d轴与转子磁链Ψr方向一致，这样dq坐标系旋转速度与磁场旋转速度相同，电机内部磁场相对位置固定。此时，ABC三相电流在dq坐标系中分解为沿d轴方向的励磁电流分量Ids及沿q轴方向的转矩电流分量Iqs，两分量相互独立，由此电磁力矩可简化为[17]

(20)

在式(20)中，转子磁链Ψr由励磁电流分量Ids与电机参数决定，与定子转矩电流分量Iqs无关，当电气参数为常数时Te与Iqs成正比，此时若Te波动则Iqs也会以同频率进行波动。Park变换属于线性变换，Iqs波动时三相电流也发生对应频率的波动，导致Ids与Iqs同频率波动。由此Td以fd为频率波动时，dq坐标系中电流分量可表示为

(21)

在异步电机中磁场旋转速度等于电机定子电流变化速度，由此dq坐标坐标系转速ω=2πfe，fe为电机定子电源频率。电流Park逆变换公式可写为

(22)

将式(21)代入式(22)中，可求出定子电流，并使用三角函数积化和差公式进行整理，可得定子A相电流如下

(23)

由式(23)可以看出，在Td激励下定子电流特征频率除了电源频率fe之外，还出现了fe-fd，fe+fd与激励频率有关的频率成分。在实际中激励频率fd常常大于电流频率fe，由于余弦函数为偶函数，进一步地边频成分可表示为|fe±fd|。传动系统振动给电机转子带来动态激励，造成电机轴负载的波动，从而电流频率会受到机械部分频率调制作用，产生相应边频。

4 电机-齿轮系统机电耦合仿真模型

4.1 机电耦合仿真模型搭建

使用MATLAB/Simulink求解机电耦合模型：首先，使用Simulink模块搭建异步电机及其电流滞环控制模型；其次，使用S-Function函数建立电机-齿轮系统动力学方程，电磁力矩等外部激励作为输入系统；最后，异步电机输出电磁力矩作用于动力学系统，由动力学系统计算出电机轴转速而后输入电机系统，完成机电耦合模型的建立。Simulink仿真模型搭建如图6所示。行星齿轮主要参数如表1所示，电机主要参数如表3所示。

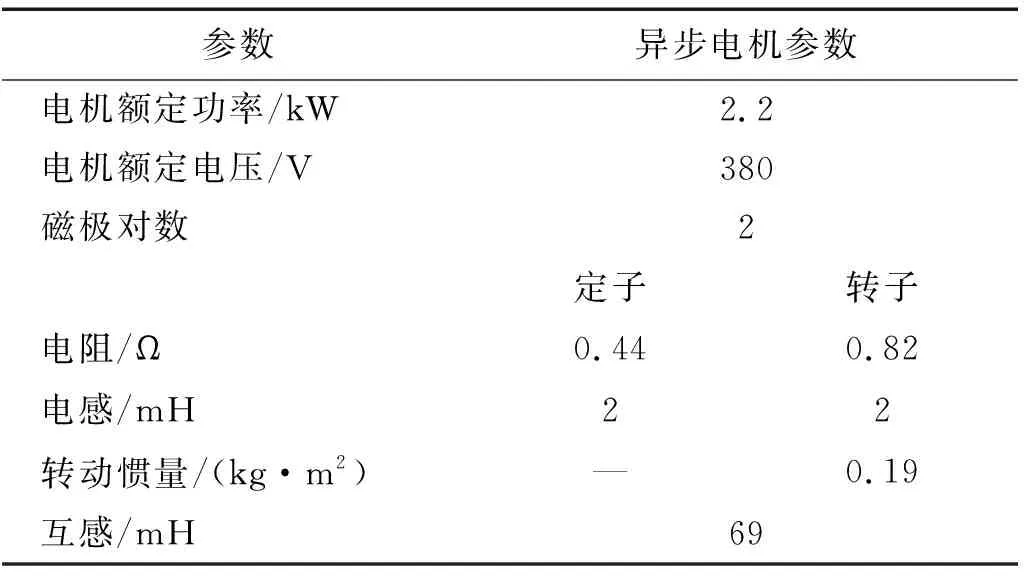
参数异步电机参数电机额定功率/kW2.2电机额定电压/V380磁极对数2定子转子电阻/Ω0.440.82电感/mH22转动惯量/(kg·m2)—0.19互感/mH69

4.2 动力学仿真结果与验证

在仿真中设置电机目标转速为1 000 r/min，负载转子处添加恒定负载为30 N·m，选用ode4龙格库塔固定步长算法对电机-齿轮系统进行求解。在该工况下，仿真得出的太阳轮x，y向振动加速度，并投影到大地坐标系Y向，其时频响应如图7所示。

本文行星齿轮模型参数与文献[18]相同，且在相同工况下，仿真得出的振动加速度响应的时域幅值，特征频率分布与曹金鑫的试验结果相符，验证了本文动力学模型的有效性，为后续定子电流响应分析提供了可靠的动力学模型。

5 传动系统对定子电流响应影响分析

5.1 齿轮时变啮合刚度对定子电流响应的影响

为研究齿轮时变啮合刚度对定子电流响应的影响，同时为时变轴承刚度作用下的仿真结果提供对照，将行星齿轮系统中的轴承刚度取为常数。电机目标转速设置为600 r/min，负载转子处添加恒定负载为30 N·m，系统响应稳定时，对应电流频率fe1为21.2 Hz，行星齿轮系统啮合频率fm1=Zpωp为202.1 Hz。

电机轴扭振速度频谱如图8(a)所示，电磁力矩频谱如图8(b)所示，电机定子A相电流频谱如图8(c)所示。动态啮合力作用在齿轮的转动上，是电机轴扭振的主要激励源，所以在电机轴扭振速度频谱图8(a)中，其主要峰值由啮合频率fm1及其倍频组成；电机轴的扭振直接作用于电机转子，其作用关系如式(12)所示，扭振产生的力矩引起电磁力矩的同频率响应。同受电流影响，在图8(b)中还出现了由电源频率及PWM发生器产生的电流频率；在定子电流频谱图8(c)中，其峰值主要为电流频率，同时也包含与机械振动频率相调制频率为|fe1±nfm1|的峰值。由于电机转子相对较大的转动惯量及电机定子绕组产生的电感，使得电机系统对高频激励不敏感，具有低通滤波的性质，导致从电机轴扭振到电磁力矩再到定子电流，高频部分幅值逐级衰减。

5.2 太阳轮处时变轴承刚度对定子电流响应的影响

为研究太阳轮处时变轴承刚度对定子电流响应的影响，在引入太阳轮处的时变轴承刚度激励影响，并进行仿真。仿真工况设置与5.1节相同，该条件下时变轴承刚度频率fb1=Nbωs为90.6 Hz。

电机轴扭振速度频谱如图9(a)所示，电磁力矩频谱如图9(b)所示，电机定子A相电流频谱如图9(c)所示，电机定子A相电流频谱0～500 Hz局部放大如图9(d)所示。引入时变轴承刚度后，齿轮x，y方向的振动响应受其激励包含了时变轴承刚度频率，在计算动态啮合力时，齿轮时变啮合刚度与该振动响应相乘，出现了齿轮啮合频率与时变轴承刚度频率在频域上的卷积，所以与图8(a)相比，图9(a)中出现|n1fm1±n2fb1|的频率调制，n1，n2分别为啮合刚度、轴承刚度的谐波次数；同时也可以看出相对于啮合刚度，时变轴承刚度引起的激励较小。|n1fm1±n2fb1|以与4.1节中所述相同的方式传递到电机系统如图9(b)及图9(c)所示。在定子电流频谱中，|n1fm1±n2fb1|进一步与电源频率fe1产生调制，出现|fe1±(n1fm1±n2fb1)|的频率成分。由于轴承刚度引起的激励本身幅值较小，并且电机系统带有低通滤波的效果，所以轴承刚度引起的频率成分在高频部分难以观测，忽略高次谐波成分重点观察0～500 Hz低频部分响应如图9(d)所示，电流上体现出了轴承刚度频率而且低频部分的幅值更明显。

5.3 不同转速下定子电流响应

为研究不同转速下的电流响应，设置电机目标转速为1 000 r/min，其他仿真条件设置与5.2节相同，在此对系统进行仿真。该工况下，电流频率fe2为35.2 Hz，齿轮系统啮合频率fm2为336.6 Hz，时变轴承刚度频率fb2为150.6 Hz。

对比600 r/min及1 000 r/min时电机系统动态响应，在不同转速下，电机轴扭振速度频谱如图10(a)所示，电机定子A相电流频谱如图10(b)所示。由于负载不变，在不同转速下行星齿轮传动系统动态啮合力频率不同，而幅值大致相同，动态啮合力激励作用于扭振，所以在图10(a)中，不同转速下的啮合频率nfm1与nfm2所对应的峰值大致相同；在转速为1 000 r/min时，转速较高齿轮水平及竖直方向振动响应较大，所以轴承引起的边频具有更大的幅值。转速变化导致特征频率偏移也反应在了定子电流频谱中，与扭振频谱不同的是，由于负载不变转速升高系统功率升高，所以fe2的峰值大于的fe1的峰值，其次电机系统带有低通滤波的性质，|fe2±fm2|频率较高其幅值小于|fe1±fm1|处幅值。转速不同时，引起电源频率、啮合频率及轴承频率的变化，造成对应特征频率在定子电流频谱上的偏移，由此可通过定子电流频率响应监测行星齿轮传动系统及其齿轮、轴承部件的运行工况。