一类含绝对值函数问题的求导策略

蔡建华

(江苏省常州市第三中学, 213000)

高中阶段含绝对值的函数问题试卷中屡见不鲜,常考查恒成立(能成立)以及取值范围等问题.学生遇到此类问题往往感到比较棘手.其原因之一是含绝对值问题一般需要分类讨论去掉绝对值符号,二是含参数问题一般需要结合参数取值范围分类讨论,而这恰恰是学生的能力薄弱之处.那么如何避免此类痛点?这是一个值得思考的问题.

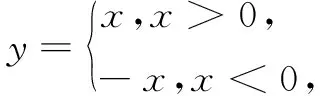
例1已知f(x)=ex|x-a|在(-1,2) 单调递增,则实数a的取值范围是______.

评注本题用常规解法比较繁琐,而采用上述方法能避免分类讨论,方便了对导函数的符号判别,起到化繁为简的效果.

例2对于任意x∈[1,3],不等式x|x-a|+2≥a(a≥1)恒成立,求a的取值范围.

解问题等价于(x|x-a|)min≥a-2,x∈[1,3].令g(x)=x|x-a|,则

例3设函数f(x)=(x-a)|x-a|-x|x|+2a+1(a<0),若存在x0∈[-1,1],使f(x0)≤0,则a的取值范围是______.

解本题是存在性问题,依题意,仅需f(x)min≤0,x∈[-1,1].由绝对值函数求导策略,f′(x)=2(|x-a|-|x|),即

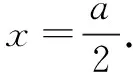
评注该题对原函数求导后,要确定导函数f′(x)=2(|x-a|-|x|)的符号,仍需要通过绝对值函数常规处理方法,利用分类讨论得出导函数图象,确定原函数在[-1,1]的单调性.