函数思想在高考解题中的应用*

刘兰茵

(江苏省扬州大学数学科学学院,225002)

函数描述了自然界中量与量之间的依存关系,反映了一个事物随着另一个事物变化而变化的关系和规律．函数思想是指运用运动和变化的观点去研究和分析数学问题中的数量关系,通过建立函数模型或构造辅助函数,运用函数的图象和性质去分析问题、转化问题和解决问题[1].在高考数学试题中,函数思想不仅是解决函数问题的重要思想方法,而且在方程、不等式、数列、向量、几何等方面应用非常广泛.

一、用函数思想解决方程问题

方程的本质是建立已知量与未知量之间的等量关系,是构建由已知探索未知的桥梁.由于方程f(x)=0的根是函数y=f(x)图象与x轴交点的横坐标,因此静态的方程问题常常可以转化为动态的函数问题,运用函数思想进行解决.

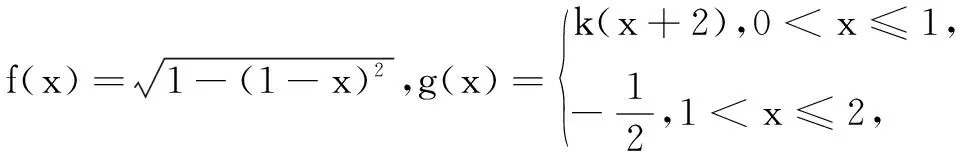
解f(x)=g(x)有8个不同的实数根等价于相应两个函数的图象在(0,9]有8个交点.由f(x)在(0,2]的图象是以(1，0)为圆心、半径为1的上半圆，结合f(x)是奇函数且周期为4，可画出它在(0，9]上的草图，如图1.

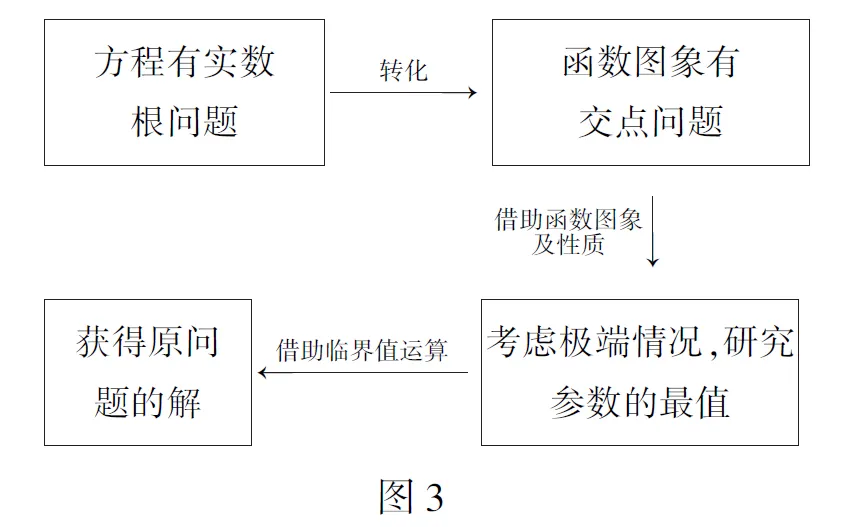
评注本题借助函数图象求参数的取值范围,主要考查学生直观想象和逻辑推理的核心素养.其思维流程框图如图 3所示.

二、用函数思想解决不等式问题

不等式与函数也有着密切联系,不等式f(x)>0(f(x)<0)的解是函数y=f(x)在x轴上方(下方)图象对应的点的横坐标的取值范围.因此,借助函数思想对不等式变形,构造辅助函数解决不等式问题也是一个重要的数学方法.

例2(2016年全国高考题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(1)求a的取值范围;

(2)设x1,x2是f(x)的两个零点,证明:

x1+x2<2.

解(1)略.

(2)不妨设x1f(2-x2),即f(2-x2)<0.

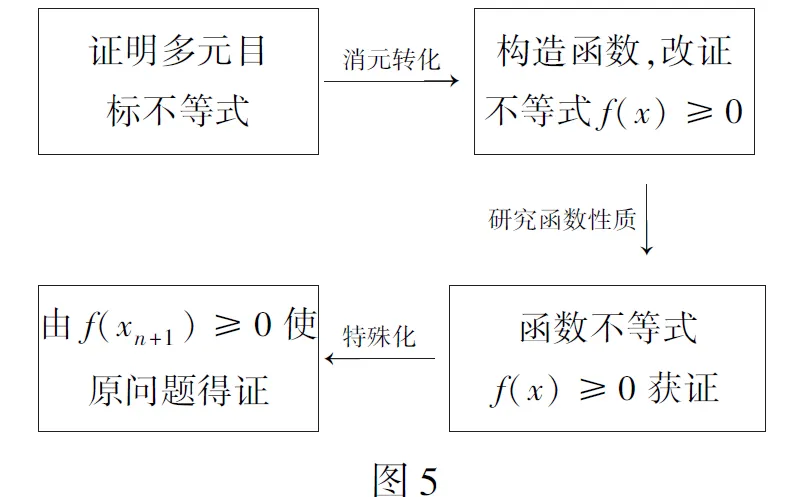
因为f(2-x2)=-x2e2-x2+a(x2-1)2,而f(x2)=(x2-2)ex2+a(x2-1)2=0,所以f(2-x2)=-x2e2-x2-(x2-2)ex2.设g(x)=-xe2-x-(x-2)ex,则g′(x)=(x-1)(e2-x-ex),当x>1时，g′(x)<0,有g(x)

评注本题借助函数证明不等式,考查学生的数学抽象和逻辑推理等核心素养.其思维流程框图如图 4所示.

(A)a

(C)b

综上，选B.

评注本题设置的问题是实数比大小问题，通过观察与分析特点，构造辅助函数将其一般化，使问题获解，有效考查了学生数学抽象、数学运算等核心素养.

三、用函数思想处理数列问题

数列是一种特殊的函数.在数列问题求解过程中,可通过一般化构造辅助函数,将数列问题转为函数问题,借助函数的性质进行求解,再由特殊化回到原问题,得到解答.

例4(2017年浙江高考题)已知数列{xn}满足x1=1,xn=xn+1+ln(1+xn+1),证明：当n∈N*时，

(1)0

解(1)略.

(3)略.

评注本题第(2)问利用递推关系消元转化成一元不等式,为利用函数研究不等式铺平了道路,能有效考查学生数学抽象、逻辑推理和数学运算等核心素养.其思维流程框图如图 5所示.

四、用函数思想解决向量问题

向量具有数与形两方面的特征,所以向量问题兼具代数问题与几何问题的双重特性.由于函数具有解析式和图象的表达方式,因此向量问题可借助函数的数和形的性质进行解决,尤其是在向量的模长求最值问题中.

例5(2017年浙江高考题)已知a,b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是______,最大值是______.

评注本题主要考查学生数学抽象、逻辑推理和数学运算核心素养.求解的关键是引入参数θ，将向量问题转化为三角函数求最值问题,其思维流程框图如图6所示.

五、用函数思想解决立体几何问题

在立体几何的相关问题中,对于求面面、线面、线线之间夹角的最值问题,以及求立体图形的表面积或体积的最值问题,最终常借助函数的单调性和最值进行解决.

例6(2016年浙江高考题)如图7,在∆ABC中，AB=BC=2，∠ABC=120°.若平面ABC外的点P和线段AC上的点D，满足PD=DA，PB=AB，则四面体PBCD体积的最大值是______.

解依题意，∆PBD可视为∆ABD绕BD旋转得到的.因此，当四面体PBCD的体积最大时，平面PBD⊥平面ABC，此时高h为点P到直线BD的距离，即点A到直线BD的距离.

评注本题形式上是几何问题,但对几何直观、数学抽象、代数运算的要求较高.求解时需要用运动变化的观点分析问题,通过引入变量建立函数关系,利用换元法简化运算,最后借助导数法使问题获解.其思维流程如图8所示.

通过以上问题的求解,可以看出函数思想是高考考查的重要数学思想方法,掌握函数思想有助于帮助学生找到解题思路,提高解题效率.正如日本数学教育家米山国藏所言:“学生们在初中或高中所学到的数学知识,在进入社会后,几乎没有什么机会应用,这种作为知识的数学,所以通常是出校门后不到一两年,很快就忘掉了.然而,不管他们从事什么业务工作,唯有深深铭刻于头脑中的数学的精神,数学的思维方法、研究方法、推导方法和着取点等,却随时随地发挥作用,使他们受益终生[2].”因此,教师在课堂教学中,在培养学生基础知识和基本技能的同时,更应该注重培养学生对数学思想方法的应用意识及应用能力,发展学生思维与创造性,促进学生数学核心素养的形成.