是“巧合”还是“必然”
——一道不等式问题解答的释疑
2022-10-26田加贵
高中数学教与学 2022年17期
田加贵
(云南师范大学附属中学,650106)

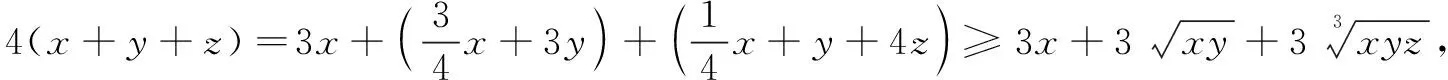
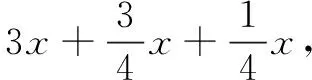


其次,根据以上这一想法,我们可以尝试解答原题了.虽然问题的难度加大了,并不在一个平台上,但思想方法还是可以借鉴的.

x+y+z
=kx+mx+ty+(1-k-m)x+(1-t)y
+z
(*)
该不等式取等号时必有mx=ty且(1-k-m)x=(1-t)y=z,即有(1-k)x=y,得(1-k)xt=yt=mx,m=(1-k)t.
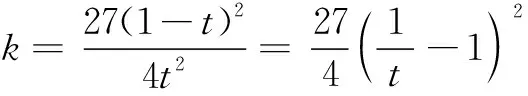
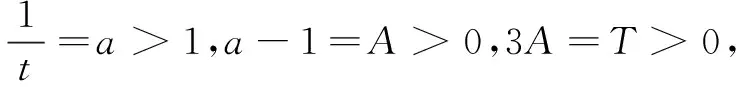
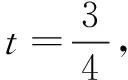
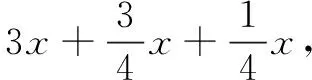
评注本题的上述探究表明在解决比较困难的问题时,可以将问题降低一些难度,寻求出思路,再推广至原问题.本题是将三个未知数的最值问题转化为两个未知数的最值问题进行探求方法思路,进而是将x分拆为三部分,将y分拆为两部分,而z保持不动.这种想法很朴素,也很简单,尽管不太好对x+y+z进行分拆,但我们要相信许多问题的背后往往有其章法可寻,要求我们必须具备一定的观察问题、分析问题和解决问题的能力.这需要我们长期的多学习、多总结,这样在遇到一些较为困难的问题时,才会有更多更宽的思路和想法对其进行解决,或对一些问题的既成解决方式方法和疑点疑问释然释怀.
