“曲曲联立”产生的错误及错因分析

蒋雪雷

(江苏省泗阳中学，223700)

在学习解析几何有关内容时,很多情况都是联立直线与圆锥曲线方程组解决问题,但是也有一些情况是将两个二次曲线进行联立求解的.有学生在“曲曲联立”的解题过程中遇到了一些问题和困惑,本文对此总结如下.

一、“点差法”失效

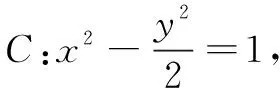
解当直线l的斜率不存在时,l与双曲线只有一个交点(1,0),此时结论不成立.

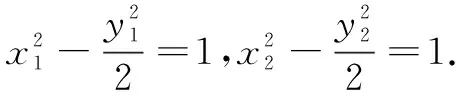
检验:联立直线l的方程y=2x-1与双曲线方程,得2x2-4x+3=0.因为Δ=-8<0,故方程无实数根,直线l不存在.

综上,满足题设的直线l不存在.

剖析很多学生都不理解,在用点差法处理这个问题时,直线方程已经求出来了,为什么最后的结果却不存在?解答的最后为什么要去检验?点差法都需要检验吗?

事实上,在上述用点差法解题的过程中,若先设点A(x1,y1),B(x2,y2)再往下求解,则点A,B在双曲线上就是后续推理过程中的前提条件,但这个前提条件正确吗?在检验之前是不确定的,而后面的检验正是在验证确认这个前提条件的正确性.由此可见,这样利用点差法解决的问题都需要检验.

与此同理的是:我们在求两圆的相交弦方程时,两圆方程相减,只有在这两圆相交时得到的方程才是相交弦方程;若是两圆相离,也能减出一条直线方程(两圆的根轴),但这时的两圆却是没有公共点的.

二、“韦达定理”失效

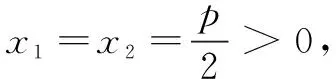
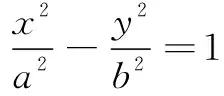
若不加这个限制条件,可得到如下结论:令f(x)=b2x2-2pa2x-a2b2,则f(-a)=2pa3>0,f(0)=-a2b2<0,由零点存在性定理知f(x)在(-a,0)内有一个零点,这也就是上述解法中的那个负根,也是方程b2x2-2pa2x-a2b2=0的一个“增根”.又由f(a)=-2pa3<0及二次函数的开口向上,知f(x)在(a,+∞)内有一个零点,这个零点才是抛物线与双曲线在第一象限中关于x轴对称的两个交点的横坐标.