2021年广西平面几何预赛题的向量证法
2022-10-26龚新平
高中数学教与学 2022年17期
龚新平
(上海市育才中学,201801)
向量是一种重要的数学工具,它在平面几何等诸多学科方面有着重要应用,很多数学结构或关系都可以用向量数量积和向量分解基本定理等形式来精准表达.笔者发现2021年各省市高中数学预赛试题中很多平面几何问题都可以用向量方法来证明.本文将对2021年广西平面几何预赛题给出向量法证明,现整理出来和大家分享.
一、问题呈现

二、向量证法

①

λc2+μb2=λ2c2+2λμbccosA+μ2b2.
②
③
mc2+nb2=m2c2+2mnbccosA+n2b2.
④
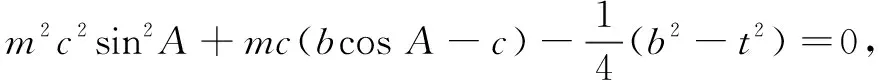

λc+μb=mc+nb.
⑤
⑥
(4)最后,我们证明等式⑥ 是成立的.
所以,结论AP⊥FG得证.

三、结束语
数学竞赛中的平面几何问题一般都要用到一些重要定理, 如梅涅劳斯定理、塞瓦定理等,本文仅利用平面向量分解基本定理,结合向量数量积运算,并用新教材中向量投影的概念表达了“四点共圆”,成功建立了系数λ,μ的二元二次方程组,通过适当的代数变形,证明了原结论的等价命题,这些是解决问题的核心与关键!有兴趣的读者可进一步尝试运用向量方法来解答2020年全国联赛加试部分的平面几何问题.
