非常规不等式的解法探究
2022-10-26田素伟
田素伟
(上海市泥城中学)
不等式是高中数学考查的重点内容,也是高考必考的内容,对于常规的各类不等式的基本解法,这里不再重复.而有很多数学知识以不等式为载体,考查最值、不等关系以及恒成立等问题.这类不等式问题构思新颖、条件隐蔽、技巧性强、解法灵活.那么如何正确解答这类问题? 下面以具体的题目来探究一些非常规不等式的解法.
1 含偶次方根的无理不等式

点评本题极容易忽视偶次方根的被开方数是非负数这一隐含条件,所以在解题时要充分考虑题中的限制条件.
2 构造函数解不等式

当x1>x2时,f(x1)-f(x2)<x1-x2,即f(x1)-x1<f(x2)-x2;当x1<x2时,f(x1)-f(x2)>x1-x2,即f(x1)-x1>f(x2)-x2.
设g(x)=f(x)-x,则g(x1)=f(x1)-x1,g(x2)=f(x2)-x2.当x1>x2时,g(x1)<g(x2);当x1<x2时,g(x1)>g(x2),所以g(x)=f(x)-x在定义域R上单调递减.又因为y=f(x)是定义域为R 的奇函数,所以f(0)=0,所以g(0)=f(0)-0=0.
由f(m)>m,得f(m)-m>0,又g(m)=f(m)-m,g(0)=0,所以g(m)>g(0),而g(x)在R 上单调递减,所以m<0.
综上,不等式f(m)>m的解集为{m|m<0}.
点评根据题意可构造函数g(x)=f(x)-x,利用单调函数的定义可以判断函数g(x)=f(x)-x在定义域R 上单调递减,由g(0)=0,则f(m)>m等价于g(m)>g(0),再根据函数的单调性脱去“f”.
3 利用反函数的性质解不等式

点评根据反函数的性质,本题可转化为当x>3时,求函数f(x)=(x>0)的值域,这样可以不用求反函数的解析式,只需解不等式即可,简化运算.本题考查反函数的概念与性质、函数的单调性以及函数值域的求法.
4 利用函数的单调性解不等式
例4若定义在区间[-3,3]上的函数f(x)=,求f(x+1)+f(2x-1)>0的解集.

点评先判断函数在定义域上的奇偶性和单调性,再根据函数的单调性和奇偶性将函数不等式转化为关于自变量的不等式,注意不要忽略函数的定义域.
例5已知定义在R上的函数y=f(x+1)是偶函数,且在(0,+∞)上单调递增,求满足f(2x)>f(x+2)的x的取值范围.
解析因为y=f(x+1)是偶函数,所以f(-x+1)=f(x+1),故函数y=f(x)的图像关于直线x=1对称.
因为函数f(x+1)在(0,+∞)上单调递增,所以函数f(x)在(1,+∞)上单调递增.
又由f(2x)>f(x+2),得|2x-1|>|x+2-1|,即|2x-1|>|x+1|,两边平方并化简得x2>2x,解得x>2或x<0.
综上,x的取值范围为(-∞,0)∪(2,+∞).
点评本题利用函数的性质,确定函数f(x)关于直线x=1对称,且在(1,+∞)上单调递增,结合函数对称性和单调性去“f”再解不等式.
5 利用向量构造不等式

因为|m|=1,|n|=|a|,所以
f(x)=m·n=|m|·|n|cosθ≤|m|·|n|≤|a|.
又因为fmax(x)=2,所以|a|=2,解得a=±2,故实数a的值为2或-2.
点评本题考查根据函数最值求解参数的值,解题关键是能够利用化归转化思想,将函数表示为向量数量积的形式,进而根据m·n≤|m|·|n|构造不等式确定参数的取值范围.
6 与正整数n 有关的不等式

点评对于含(-1)n的不等式要分为n为奇数和n为偶数两种情况讨论,在利用单调性、最值和极限思想解题时,需要注意在正整数中奇数的最小值是1,而偶数的最小值是2.
7 利用函数图像数形结合解不等式
例8(2020年北京卷6)已知函数f(x)=2xx-1,则不等式f(x)>0的解集是( ).
A.(-1,1) B.(-∞,-1)∪(1,+∞)
C.(0,1) D.(-∞,0)∪(1,+∞)
解析f(x)>0等价于2x>x+1,在同一平面直角坐标系中作出y=2x和y=x+1的图像,如图1所示.两个函数图像的交点坐标为(0,1),(1,2),不等式2x>x+1的解是函数y=2x的图像位于函数y=x+1的图像上方的部分所对应的x的取值范围.观察图像可知:不等式2x>x+1的解为x<0或x>1,所以不等式f(x)>0的解集为(-∞,0)∪(1,+∞),故选D.
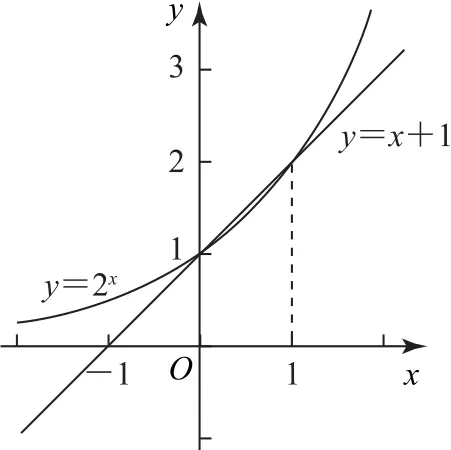
图1
点评在同一平面直角坐标系中作出函数y=2x和y=x+1的图像,观察图像可得结果,对于超越不等式常利用函数图像求解集.
8 与取整函数有关的不等式
例9对于实数x,设[x]表示不超过x的最大整数,则不等式[x]2-3[x]-10≤0的解集是_________.
解析因为[x]2-3[x]-10≤0,所以-2≤[x]≤5,故-2≤x<6,从而所求不等式的解集是{x|-2≤x<6}.
点评根据不等式先解析出[x],进而根据[x]的定义即可得到答案,这里要注意不等式的端点的取值.
9 与分段函数有关的不等式

综上,m的取值范围是(-1,0)∪(1,+∞).
点评本题考查对数不等式的求解问题,解题关键是能够写出函数f(m)和f(-m)的解析式,再利用对数函数的性质求解,考查了分类讨论的数学思想.
(完)
