二次函数与一元二次方程、不等式章节小测

王位高

(广东信宜教育局教研室)

(本试卷共22小题,满分150分,考试用时120分钟)

一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.)

1.已知集合M＝{x|－4＜x＜2},N＝{x|x2－x－6＜0},则M∩N＝( ).

A.{x|－4＜x＜3} B.{x|－4＜x＜－2}

C.{x|－2＜x＜2} D.{x|2＜x＜3}

2.下列不等式的解集为R的是( ).

A.x2＋x＋1＜0 B.x2＋2x＋1＞0

C.－x2＋x＋1≤0 D.x2＋x＋1＞0

3.已知关于x的方程x2＋mx＋m＝0有两个实数根,则m的取值范围为( ).

A.m≥4 B.m＞4或m＜0

C.m≥4或m≤0 D.0＜m＜4

4.已知关于x的不等式ax2＋bx＋c＜0的解集为{x|x＜－1或x＞4},则下列说法正确的是( ).

A.a＞0

B.不等式ax2＋cx＋b＞0的解集为

C.a＋b＋c＜0

D.不等式ax＋b＞0的解集为{x|x＞3}

5.已知函数y＝ax2＋2bx－c(a＞0)的图像与x轴交于A(2,0),B(6,0)两点,则不等式cx2＋2bx－a＜0 的解集为( ).

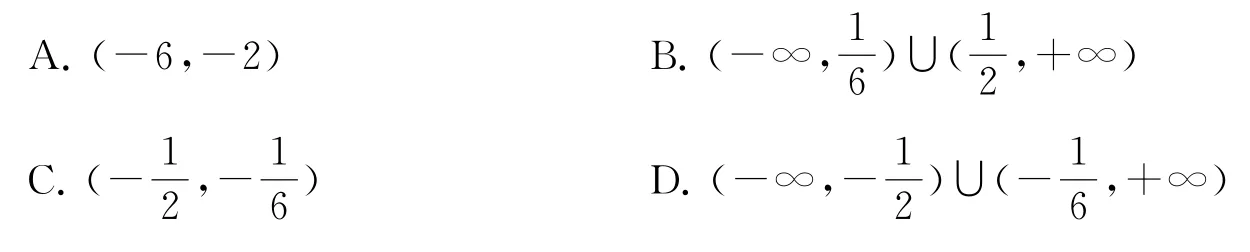
6.已知命题“∀x∈R,4x2＋(a－2)x＋＞0”是假命题,则实数a的取值范围为( ).

A.(－∞,0]∪[4,＋∞) B.[0,4]

C.[4,＋∞) D.(0,4)

7.若不等式x2＋ax＋1≥0对于一切x∈(0,]恒成立,则a的最小值是( ).

8.已知关于x的不等式ax2＋2bx＋4＜0的解集为(m,),其中m＜0,则的最小值为( ).

A.－2 B.1

C.2 D.8

二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求的.全部选对的得5分,有选错的得0分,部分选对的得2分.)

9.若关于x的一元二次方程(x－2)(x－3)＝m有实数根x1,x2,且x1＜x2,则下列结论中正确的说法是( ).

A.当m＝0时,x1＝2,x2＝3 B.m＞－

C.当m＞0时,2＜x1＜x2＜3 D.当m＞0时,x1＜2＜3＜x2

10.已知集合{x|x2＋ax＋b＝0,a＞0}有且仅有两个子集,则下列选项中结论正确的是( ).

A.a2－b2≤4

B.a2＋≥ 4

C.若不等式x2＋ax－b＜0的解集为{x|x1＜x＜x2},则x1x2＞0

D.若不等式x2＋ax＋b＜c的解集为{x|x1＜x＜x2},且|x1－x2|＝4,则c＝1

11.已知方程x2＋mx＋n＝0及x2＋nx＋m＝0分别各有两个整数根x1,x2及x3,x4,且x1x2＞0,x3x4＞0,则下列结论一定正确的是( ).

A.x1＜0,x2＜0,x3＜0,x4＜0 B.x1＋x2＋x3＋x4≥－8

C.n≤m＋1 D.n＋m≥8

12.关于x的一元二次不等式x2－2x－a≤0的解集中有且仅有5个整数,则实数a的值可以是( ).

A.2 B.4 C.6 D.8

三、填空题(本题共4小题,每小题5分,共20分.)

14.已知当a∈[0,2]时,不等式ax2＋(a＋1)x＋1－恒成立,则x的取值范围为_________.

15.若关于x的不等式x2－(m＋2)x＋2m＜0的解集中恰有3个正整数,则实数m的取值范围为________.

16.已知关于x的不等式为(ax－1)(x＋1)≤0(a∈R),若a＝1,则该不等式的解集是________,若该不等式对任意的x∈[－1,1]均成立,则a的取值范围是_________.

四、解答题(本题共6小题共70分.解答时应写出文字说明、证明过程或演算步骤.)

17.(10分)求不等式x2－5x＋6＞0的解集.

18.(12分)在①{1,a}⊆{a2－2a＋2,a－1,0},②关于x的不等式1＜ax＋b≤3的解集为{x|3＜x≤4},③一次函数y＝ax＋b的图像过A(－1,1),B(2,7)两点,这三个条件中任选一个,补充在下面的问题中并解答.

问题:已知________,求关于x的不等式ax2－5x＋a＞0的解集.

19.(12分)设函数y＝ax2＋bx＋3(a≠0).

(1)若不等式ax2＋bx＋3＞0的解集为(－1,3),求a,b的值;

(2)若a＋b＝1,a＞0,b＞0,求的最小值.

20.(12分)请回答下列问题:

(1)若关于x的不等式x2－3x＋2a2＞0(a∈R)的解集为{x|x＜1或x＞b},求a,b的值;

(2)求关于x的不等式ax2－3x＋2＞5－ax(a∈R)的解集.

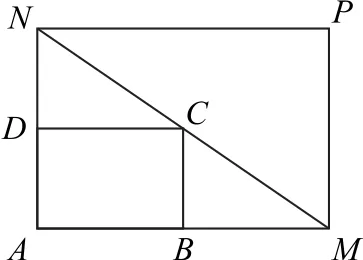
21.(12分)某建筑队在一块矩形地块AMPN上施工,规划建设占地如右图中矩形ABCD的学生公寓,要求定点C在地块的对角线MN上,B,D分别在边AM,AN上.

(1)若AM＝30 m,AN＝20 m,求AB和AD分别为多少米时,矩形学生公寓ABCD的面积最大? 最大值是多少?

(2)若矩形AMPN的面积为600 m2,则学生公寓ABCD的面积是否有最大值?若有,求出最大值;若没有,说明理由.

22.(12分)函数f(x)＝|x－1|＋|x－a|的图像关于直线x＝2对称.

(1)求a的值;

(2)若f(x)≥x2＋m的解集非空,求实数m的取值范围.