高中数学中基本不等式的常见问题及处理策略

郭兴甫

(云南省会泽县东陆高级中学校)

基本不等式是高中数学的重要内容,也是高考、高校自主命题的热点内容,其结构简洁、形式优美.基本不等式主要用于处理与最值相关问题以及不等关系的探求和论证.基本不等式常与函数、数列、解析几何、平面向量等相关知识相结合,考查数学建模、逻辑推理等数学素养.有时不能直接利用基本不等式解决问题,需要对条件改造、变形、配凑,因此基本不等式是培养学生分析问题、解决问题能力的重要载体.本文就基本不等式常见问题及处理策略进行解析,以期对读者的复习有所帮助.

1 直接利用基本不等式求最值

例1(1)(多选题)若a＞0,b＞0,且a＋b＝4,则下列不等式成立的是( ).

综上,选BD.

(2)若a＞0,b＞0,由基本不等式得

点评利用基本不等式直接求一个式子的最值时,要注意“一正、二定、三相等”的原则.即一正是要判断各项是否为正数;二定是要看和或积是否为定值(和定积最大,积定和最小);三相等是一定要验证等号能否成立(注意两点,一是等号成立时变量是否在定义域内,二是多次用不等式时等号能否同时成立).以上三点缺一不可.

2 通过配凑系数后利用基本不等式求最值

例2设正实数a,b满足ab(a＋b)＝4,则2a＋b的最小值是_________.

解析由正实数a,b满足ab(a＋b)＝4,故利用待定系数法配凑系数,使用均值不等式,则有

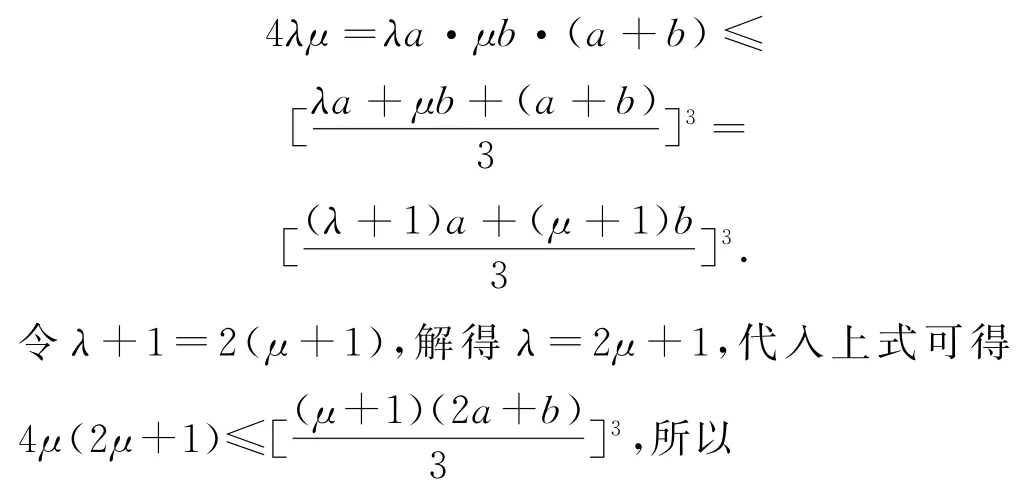
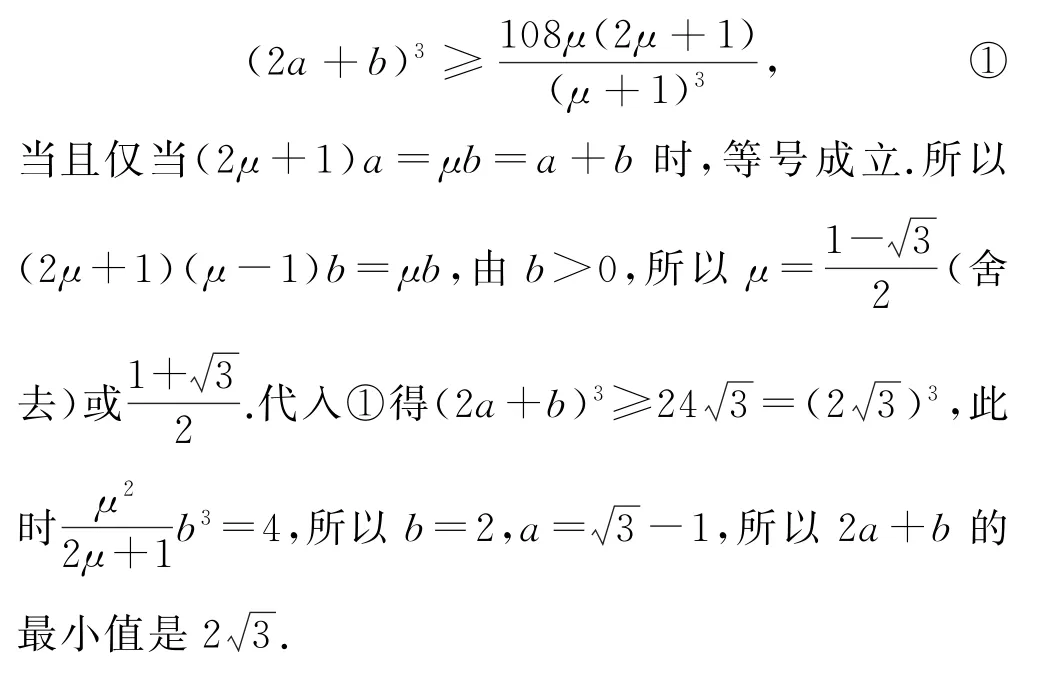
点评本题初看不易入手,但如果观察到题设条件是三个因式的积的形式,则易联想到基本不等式积定和最大的法则,通过配凑积中因式的系数,把和转化为关于结论的一个代数式,进而巧妙地解决问题.同时也可以对结论进行等价变形后结合约束条件进行配凑,使之满足基本不等式的条件.在配凑因式的系数时,可以通过待定系数法求出需要的系数.解决本题的关键是审清条件和结论之间的关系,把结论看成整体,利用整体思想和基本不等式的条件配凑系数,易错点是忽视等号成立的条件.

3 通过消元再利用基本不等式求最值

例3正实数x,y满足xy(x＋y)＝4,则2x＋y的最小值为( ).

点评本题考查了利用消元法结合基本不等式求最值的应用,用约束条件中的一个变量表示出另一个变量,或将约束条件及所求代数式进行变形,使其满足利用基本不等式的条件,再采用恰当方法求最值.同时要注意变形过程中的等价性,否则容易出错.

4 通过常数代换利用基本不等式求最值

点评常数代换法的基本步骤:一是根据已知条件或其变形确定定值(常数);二是把确定的定值(常数)变形为“1”;三是把“1”的表达式与所求最值的表达式相乘(或相除),进而构造和或积的形式;四是利用基本不等式求解最值.

5 通过变项法求多变量最值

点评本题对已知条件和所求最值的代数式恒等变形之后进而应用基本不等式求解.使用基本不等式求最值,有时需要从已知条件、求解目标代数式这两个方面进行变换,以达到符合基本不等式条件的目的,同时需要注意等号是否成立.

6 多次利用基本不等式求最值

点评在求解最值或证明不等式时,如果多次使用基本不等式,要根据各次不等式中等号成立的条件是否一致确定最后等号是否成立,即等号成立的条件要同时满足,否则容易产生错误.

7 利用基本不等式判断不等式是否成立

例7(多选题)已知a＞0,b＞0,且a＋b＝1,则下列说法中正确的有( ).

综上,选BCD.

点评利用基本不等式判断不等式正确性的基本策略是从已知不等式及问题的条件出发,借助基本不等式及性质的相关定理,经过逐步推理,将问题进行转化,其特征是根据已知条件逐步推出未知.特别地,要注意不等式串(a＞0,b＞0)的灵活应用.

8 利用基本不等式证明不等式问题

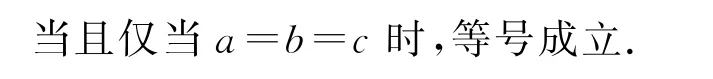
点评利用基本不等式证明不等式时,常常利用不等式的可加性.累加法是证明不等式的一种常用方法,对于不能直接使用基本不等式进行证明的问题,可重新拆分、组合,也可利用由基本不等式可加性直接得到的形如a2＋b2＋c2≥ab＋bc＋ca,a＋b＋等结论.

9 利用基本不等式解决实际问题

例9(1)现在需要制作一个长和宽分别为am和bm 的矩形大裱框,要求其长和宽使用不同的材质,长和宽材质的单价分别为10 元·m－1和20 元·m－1,在总制作费用不超过100元的条件下,可裱框相片的最大面积为( ).

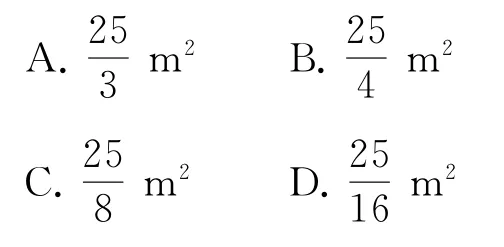
(2)某污水处理厂为使处理后的污水达到排放标准,需加入某种药剂,加入该药剂后,药剂的浓度Cmg·m－3随时间th 的变化关系可近似地用函数C(t)＝(t＞0)刻画.由此可以判断,若使被处理的污水中该药剂的浓度达到最大值,需经过( ).

A.3h B.4h C.5h D.6h

(3)某单位为节约成本,进行技术更新,将细颗粒物进行处理.已知该单位每月的处理量最少300t,最多600t,月处理成本y元与月处理量xt之间的函数关系可近似地表示为y＝－100x＋80000,则每吨细颗粒物的平均处理成本最低为( ).

A.100元 B.200元

C.300元 D.400元

解析(1)由已知得20a＋40b≤100,所以a＋2b≤5,所以

(3)由题意得每吨细颗粒物的平均处理成本为

点评利用基本不等式解决实际问题时,应先仔细阅读题目信息,理解题意,明确其中的数量关系,并引入变量,依题意列出相应的函数关系式,然后用基本不等式求解;设变量时一般要把求最大值或最小值的变量定义为函数;在求所列函数的最值时,若用基本不等式时等号无法取到,则可利用函数单调性求解.解题时要注意变量的实际意义及其取值范围.

对于基本不等式的复习,应掌握基本知识和基本方法的应用,掌握基本概念及其性质的联系,熟悉基本不等式串关系的应用,重视与其他知识的整合交会渗透,挖掘基本不等式的本质,掌握基本不等式应用的常见问题,注重基本不等式成立的条件及等价转化思想在基本不等式中的应用.同时要注重抓住基本不等式问题的核心,感悟问题本质,熟悉常考题型,善于正用、逆用、变形应用公式,配凑构建定值,创造使用基本不等式的条件,进而解决问题.

(完)