求参数取值范围问题的方法探究

陈晓明

(安徽省宁国中学)

求参数取值范围的问题经常出现在各级各类考试中,其综合性较强,主要考查函数的各种性质,考查学生的逻辑思维、运算求解等关键能力,考查学生的数学运算、逻辑推理、数学抽象等学科素养.解决问题的方法主要有分类讨论法、分离参数法、图像法、构造函数法等.下面通过具体实例对求解这类试题的方法进行探究.

例1已知函数f(x)＝(ax2－2x＋1)e－x(a∈R,e为自然对数的底数),若函数f(x)在[－1,1]上单调递减,求a的取值范围.

令g(x)＝ax2－2(a＋1)x＋3.

当a＝0 时,g(x)＝－2x＋3,在[－1,1]上,g(x)＞0,故f′(x)＜0,函数f(x)在[－1,1]上单调递减.

当a＞0时,函数g(x)＝ax2－2(a＋1)x＋3,其图像是开口向上的抛物线,且对称轴x＝＞1,故g(x)在[－1,1]上单调递减,当且仅当g(1)＝1－a≥0,即0＜a≤1 时,在[－1,1]上,g(x)≥0,f′(x)≤0,函数f(x)在[－1,1]上单调递减.

当a＜0时,g(x)＝ax2－2(a＋1)x＋3是开口向下的抛物线,当且仅当即－≤a＜0时,在[－1,1]上,g(x)≥0,f′(x)≤0,函数f(x)在[－1,1]上单调递减.

综上,参数a的取值范围为[－,1].

方法2(分离参数法) 根据题意可知f′(x)＝－e－x(ax2－2ax－2x＋3)≤0在[－1,1]上恒成立,即(x2－2x)a≥2x－3在[－1,1]上恒成立.

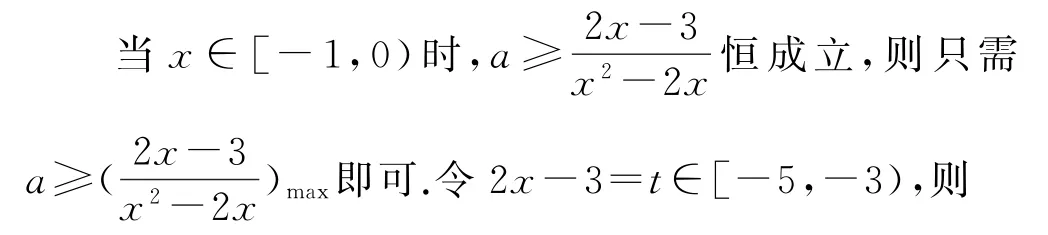
点评两种方法都是将函数的单调性问题转化为不等式恒成立问题,方法1是对参数进行分类讨论,因此最后对参数的范围求并集;而方法2 是对自变量进行分类讨论,因此最后对参数的范围求交集.

例2已知函数f(x)＝sinωx＋acosωx(ω＞0,a＞0),对任意x1,x2∈R,f(x1)＋f(x2)的最大值为4,若f(x)在(0,π)上恰有两个极值点,则实数ω的取值范围是( ).

解析方法1因为对任意x1,x2∈R,f(x1)＋f(x2)的最大值为4,所以f(x)的最大值为2,所以＝2,又a＞0,所以a＝1,故

据不完全统计，2008-2016年有关数学文化的试题共34道(数学文化的标准不同，本文采用南开大学顾沛教授的数学文化广义内涵，包含数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系等)，在高考数学试题中的分值比重已越来越大，涉及湖北、北京、上海、浙江、江苏、江西、福建、全国卷等.其中，湖北卷几乎年均有2-3题左右，全国卷从2015年开始重视，以后每年都有题目出现.为更直接地体会全国各地高考数学新课标文、理试卷中的数学文化试题，按年份列出下表(见表1)，并总结出了数学文化背景试题的一些特征：

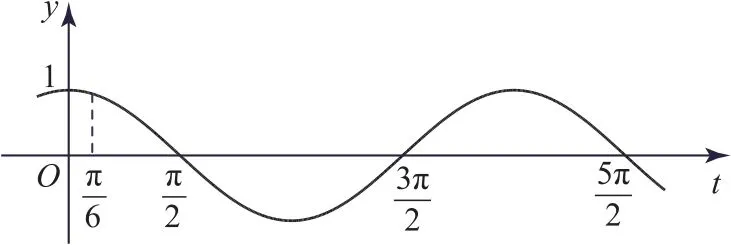
图1

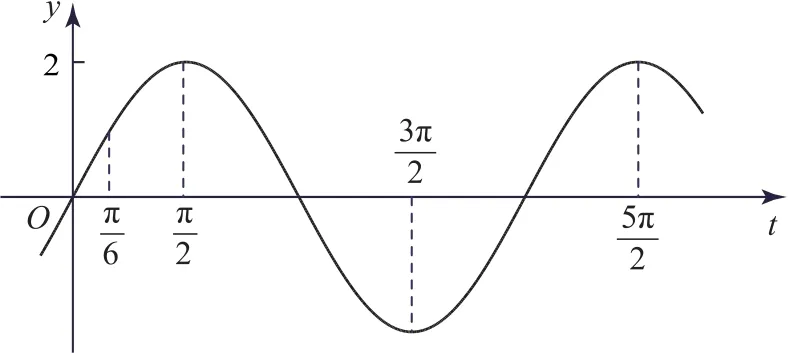
图2

点评两种方法都是通过观察函数图像判断参数的取值范围,方法1是根据原函数的极值点就是导函数的变号零点,从而根据导函数的图像判断;方法2是直接根据原函数的图像判断.另外,要注意取值范围的端点值(临界值)是否可取.

变式1函数f(x)＝2sin(ωx＋)(ω＞0)的图像在[0,2]上恰有两个最大值点,则ω的取值范围为( ).

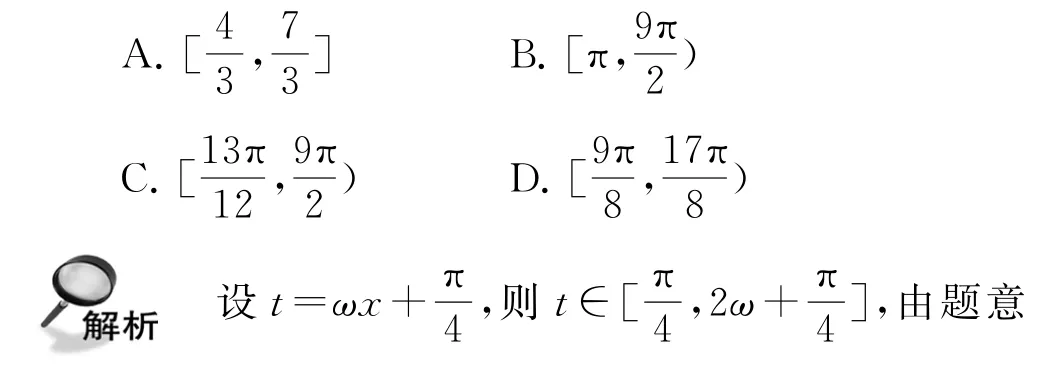
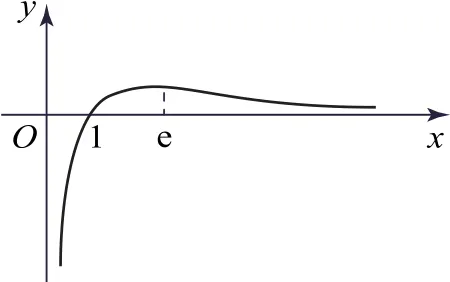
图3

点评本题通过构造函数将不等式转化为“函数值”大小关系,再利用函数的单调性将“函数值”大小关系转化为“自变量”大小关系(脱掉抽象符号“g”),进一步将恒成立问题转化为最值问题,从而求出参数的取值范围.本题是选择题,也可以利用排除法首先排除A:由已知a＞1,而＜1,所以不可能选A.

例4(2021年全国甲卷理21)已知a＞0且a≠1,函数f(x)＝(x＞0).

(1)当a＝2时,求f(x)的单调区间;

(2)若曲线y＝f(x)与直线y＝1有且仅有两个交点,求a的取值范围.

点评曲线y＝f(x)与直线y＝1有且仅有两个交点→方程有两个不同的解→构造函数g(x)＝函数g(x)的单调性→gmax(x)＝的取值范围.关于含有参数的方程根的问题,经常采用分离参数(式)法和构造新函数法,通过研究新函数的单调性确定参数范围,这是一种解决方程根问题常见的基本方法.由例3与例4知,含有参数的不等式和方程(等式),通过分离参数(式),利用构造函数法解决问题是一种重要方法,应引起我们的重视.

上述实例给出了求参数取值范围的一些具体的方法.这些方法有时也不是“独立”的,需要多种方法相互渗透,“联合”起来解决问题.无论哪种方法,理解数学概念、掌握函数的各种性质、领悟数形结合的数学思想是解决问题的根本.

笔者认为数学解题的最高境界必然是“无招”.无招的背后,必然是寻求以不变应万变的本质.数学解题中的“无招”,其实质应该是解题的通性通法.通性通法就是解决一类问题的最合理的想法、最基本的思路、最常用的方式、最普遍的操作程序.如果求参数的取值范围有“绝招”,那应该是立足课堂,抓住典型例题,让学生真正掌握解决这类问题的通性通法.

通性通法教学不仅有利于学生快速抓住数学知识的本质,形成有效解决问题的策略,而且有利于消除学生对数学学科的畏惧心理,增强学生学好数学的自信心.因此,通性通法教学应引起我们广大教师的重视,以无招胜有招,才能让学生笑傲考场.

链接练习

1.设a＞b＞c且恒成立,则实数m的取值范围是________.

2.在△ABC中,角A,B,C所对的边分别为a,b,c.已知sinA＋sinC＝psinB(p∈R),且ac＝.当角B为锐角时,参数p的取值范围是_________.

3.已知函数f(x)＝sinωxcosωx－sin2ωx(ω＞0),若函数f(x)在(,π)上单调递减,则实数ω的取值范围是________.

4.已知f(x)是定义在R 上的奇函数,且f(x＋1)是偶函数.当0≤x≤1时,f(x)＝－log2(x＋1).设g(x)＝|f(x)|＋f(|x|),若关于x的方程g(x)－mx－2＝0有5个不同的实数根,则实数m的取值范围是_________.

链接练习参考答案

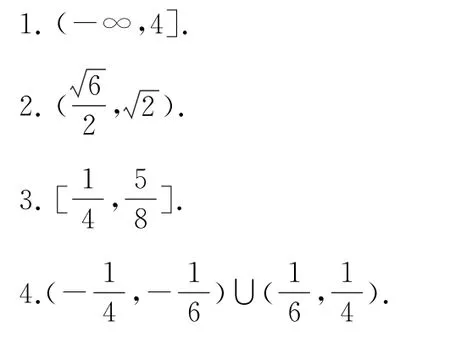
(完)