借误导悟 提升能力——以直线的倾斜角和斜率及直线的方程为例

马 骥

(甘肃省庄浪县教育局)

本文就人教版教材数学《必修二》“3.1直线的倾斜角与斜率”与“3.2直线的方程”中有关常见解题误区加以归类解析,旨在帮助读者真正厘清错误的根源,提高对有关基本知识点的到位理解与深刻认识,有利于“借误导悟”,进一步提高解题思维能力.

1 未考虑“直线的斜率是否存在”

例1已知直线l经过点P(－1,2),且直线l的倾斜角为θ,求直线l的方程.

错解1依题意,直线l的斜率k＝tanθ,又直线l经过点P(－1,2),所以由点斜式得所求直线l的方程为y－2＝(x＋1)tanθ,即

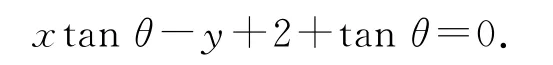
错解2设直线l的方程为y＝kx＋b,因为直线l经过点P(－1,2),所以2＝－k＋b.又直线l的斜率k＝tanθ,所以2＝－tanθ＋b,解得b＝2＋tanθ,故所求直线l的方程为y＝xtanθ＋2＋tanθ,即

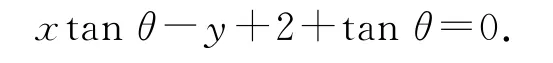
辨析先认真学习以下三个知识点:1)只有当直线的倾斜角θ≠时,直线的斜率才存在,且斜率满足k＝tanθ;2)只有当直线的斜率存在时,直线的点斜式方程y－y0＝k(x－x0)才成立;3)只有当直线的斜率存在时,直线的斜截式方程y＝kx＋b才成立.

下面再来看本题,因为直线l的倾斜角θ与的大小关系不确定,故需要讨论.据此可知,上述错解1和2的根源均是误以为θ≠,直线的斜率必存在.

正解当直线l的倾斜角θ≠时,同错解1和2均可求得直线l的方程为xtanθ－y＋2＋tanθ＝0.当直线l的倾斜角θ＝时,结合图形易得直线l的方程为x＝－1.

综上,直线l的方程为xtanθ－y＋2＋tanθ＝0或x＝－1.

点评涉及直线斜率的问题,一定要注意分析直线的斜率是否存在.若不确定直线的斜率是否存在,则应按一般情形(斜率存在)和特殊情形(斜率不存在)加以讨论.

2 未考虑“直线倾斜角的取值范围”

例2已知直线l过点A(8,6),且直线l的倾斜角是直线3x－4y－2＝0的倾斜角的一半,则直线l的方程是________.

错解设直线l的倾斜角为α,则直线3x－4y－2＝0的倾斜角为2α,且tan2α＝,即,解得tanα＝或－3,所以直线l的斜率为或－3.

又因为直线l过点A(8,6),故由点斜式可得直线l的方程为y－6＝(x－8)或y－6＝－3(x－8),即x－3y＋10＝0或3x＋y－30＝0.

辨析我们知道任意一条直线都有倾斜角,且倾斜角的取值范围是[0,π).再看上述错解中,因为2α是直线3x－4y－2＝0的倾斜角,所以2α∈[0,π),即).据此可知tanα＝－3不适合题意,应舍去.故错解的根源是没有根据直线倾斜角的取值范围进行合理取舍.

点评一般地,解题过程中涉及直线的倾斜角时,应充分关注直线倾斜角的取值范围在解题中的灵活运用,否则,极易产生错误,且不易觉察.

3 对“直线方程的截距式”理解不到位

例3一条直线过点(5,2),且在x轴、y轴上的截距互为相反数,则这条直线的方程是( ).

A.2x－5y＝0

B.x－y－3＝0

C.x－y－3＝0或2x－5y＝0

D.x－y－3＝0或5x－2y＝0

错解依题意可设所求直线方程为＝1,把点(5,2)的坐标代入直线方程解得a＝3,则所求直线方程为x－y－3＝0,故选B.

辨析先认真学习直线方程的截距式——在x轴、y轴上的截距分别为a,b(ab≠0)的直线方程为＝1.注意:这里有一个约束条件ab≠0,即直线在两坐标轴上的截距均非零.由此即知,只有当截距均非零时,上述错解才是正确的.

正解当截距均为零时,直线经过坐标原点,易知直线方程为2x－5y＝0;当截距均非零时,同上述错解知直线方程为x－y－3＝0.

综上,所求直线方程为2x－5y＝0或x－y－3＝0,故选C.

点评只有当直线在两坐标轴上的截距均非零时,才能利用直线的截距式方程解题;若直线在两坐标轴上的截距相等(或互为相反数),则应按特殊情形(截距均为零,此时直线经过坐标原点)和一般情形(截距均非零)加以讨论.常用结论:一般地,经过平面内某点(不在坐标轴上),且在两坐标轴上的截距互为相反数的直线方程可设为y＝kx(k待定)或xy－a＝0(a待定).

4 未考虑“直线方程中y 前系数是否为零”

例4若直线x＋ay－a＝0与直线ax－(2a－3)y－1＝0互相垂直,则实数a的值是( ).

A.2 B.－3或1

C.1或0 D.2或0

错解因为直线x＋ay－a＝0的斜率为－,直线ax－(2a－3)y－1＝0的斜率为,所以由直线互相垂直得－＝－1,解得a＝2,故选A.

辨析我们知道,直线方程的一般式为Ax＋By＋C＝0,其中A,B不同时为零,显然y的系数与零的关系不确定.于是,当B≠0时,直线的斜率存在,且为－;当B＝0时,直线的斜率不存在.从而,易知错解的根源在于误以为y的系数一定不为零.

正解当a≠0且a≠时,同错解知a＝2;当a＝0时,直线方程分别为x＝0和3y－1＝0,显然此时直线互相垂直,符合题意;当a＝时,直线方程分别为2x＋3y－3＝0和3x－2＝0,显然此时直线不垂直,从而不符合题意.

综上,实数a＝2或a＝0,故选D.

点评灵活运用规律“设直线l1:a1x＋b1y＋c1＝0,直线l2:a2x＋b2y＋c2＝0,则l1⊥l2等价于法向量(a1,b1)与(a2,b2)垂直,亦等价于a1a2＋b1b2＝0”,可快速来解本题,即根据题意知,aa(2a－3)＝0,解得a＝0或2,故选D.

总之,关注“3.1直线的倾斜角与斜率”与“3.2直线的方程”有关常见解题易错点的探究,有利于在解题实践的基础上,强化对所学知识的理解与认识;有利于帮助学生逐步积累解题经验,避免一些常见错误的产生,增强明辨是非的能力;有利于逐步提高分析、解决此类问题的技能技巧,进而提升解题能力.

(完)