透视二次函数常见的五大考点

江陈峰

(江苏省西亭高级中学)

作为基本初等函数,二次函数既是初中数学知识点,也是中考数学的重要考点.这足以证明二次函数的重要性.高考中对二次函数的考查往往以“三个二次”(二次函数、二次方程和二次不等式)为载体,其综合性得到加强.那么高考命题中,对二次函数是如何考查的呢?

1 二次函数的图像与性质的应用

高中的二次函数与初中研究的重点不同,初中研究其图像及其应用,而高中研究其性质及其应用.

例1函数f(x)＝(x－2)(ax＋b)为偶函数,且在(0,＋∞)单调递增,则f(2－x)＞0 的解集为( ).

A.{x|－2＜x＜2} B.{x|x＞2或x＜－2}

C.{x|0＜x＜4} D.{x|x＞4或x＜0}

解析因为f(x)是偶函数,所以b－2a＝0,则f(x)＝ax2－4a＝a(x－2)(x＋2),又因为f(x)在(0,＋∞)上单调递增,所以a＞0.由二次函数的性质不难发现,不等式f(2－x)＞0的解集是{x|x＜0或x＞4},故选D.

点评本题将一元二次函数的性质与一元二次不等式综合在一起,体现了高考对二次函数基础题考查的要求.

2 与二次函数有关的零点及方程个数

我们知道,一元二次函数至多有两个零点,而当一元二次函数中含有绝对值符号时,零点就发生了变化.带绝对值的一元二次函数时常出现在高考中,这类问题具有一定的难度.

例2已知函数f(x)＝|x2＋3x|,x∈R.如果方程f(x)－a|x－1|＝0恰好有4个互不相同的实数根,那么实数a的取值范围是_________.

解析如图1所示,将f(x)＝|x2＋3x|和g(x)＝a|x－1|的图像画在同一个平面直角坐标系中,于是原问题就转化为f(x)与g(x)的图像刚好有4个交点.当直线y＝a(x－1)与抛物线y＝x2＋3x(或直线y＝－a(x－1)与抛物线y＝－x2－3x)相切时,函数f(x)与g(x)的图像刚好有3 个交点.将y＝a(x－1)代入y＝x2＋3x,整理可得

图1

x2＋(3－a)x＋a＝0.

由Δ＝(3－a)2－4a＝0,解得a＝1或9.

又当a＝0时,f(x)与g(x)仅有两个交点,所以0＜a＜1或a＞9.

点评对于零点个数问题一般可以采用数形结合方法求解,一元二次函数也不例外,通过构造一定一动的两个函数,在动函数的图像移动中可直接找到答案.

3 二次函数零点(一元二次方程根)的分布

二次函数零点(一元二次方程根)的分布问题,出现在“函数与方程”的章节中.作为一种数学思想,函数与方程是高中数学解题必备的策略,而根的分布问题恰好体现了这个思想,所以这个考点常常出现在函数综合题中.

例3已知函数f(x)＝ax2＋bx＋c(a,b∈R,a≠0).

(1)当a＝1,b＝2 时,若存在实数x1,x2(x1≠x2)满足|f(xi)|＝2(i＝1,2),试求实数c的取值范围;

(2)若a＞0,函数f(x)在[－5,－2]上不单调,且该函数图像与x轴相切,记f(2)＝λ(b－2a),试求实数λ满足的取值范围.

解析(1)由题意知方程x2＋2x＋c＝2有两个不相等的实数根,且x2＋2x＋c＝－2无实数根,于是有所以－1＜c＜3.

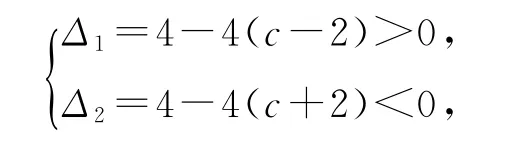
(2)因为a＞0,函数f(x)在[－5,－2]上不单调,且该函数图像与x轴相切,所以

点评本题第(1)问明显是二次函数的零点分布问题,而第(2)问看似与二次函数的零点分布问题无关,但要求λ的取值范围,必须先确定的取值范围,这时需用到f(x)在[－5,－2]上有极值点,这也是一个零点分布问题.

4 含参数的二次函数

讨论参数,是高中数学的重要题型,因此含参数的二次函数问题时常出现,难度中等或中等偏上.

例4如果函数y＝的值域是[0,＋∞),那么实数a的取值范围为( ).

A.(2,＋∞)

B.(－∞,－1)∪(2,＋∞)

C.[－1,2]

D.[0,2]

解析因为函数y＝的值域是[0,＋∞),所以t＝2ax2＋4x＋a－1能取遍[0,＋∞)上的所有实数.

当a＝0时,函数t＝4x－1能取遍[0,＋∞)上的所有实数,只需它的定义域满足[,＋∞)即可.

当a≠0时,为使t＝2ax2＋4x＋a－1能取遍[0,＋∞)上的所有实数,只需满足条件

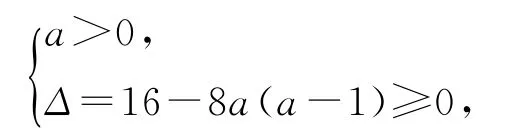
解得0＜a≤2,故0≤a≤2,选D.

点评这里需特别注意定义域是R 与值域为[0,＋∞)的区别,根据值域是[0,＋∞)可知函数t＝2ax2＋4x＋a－1能取遍[0,＋∞)上的所有实数;而定义域为R,等价于2ax2＋4x＋a－1≥0恒成立.这是两个不同的概念,不可混为一谈.

5 与二次函数有关的复合函数

在高考中,为提高二次函数的考查难度与力度,往往将二次函数问题与复合函数相结合,解题时需要弄清楚内函数与外函数之间的关系.

例5已知函数f(x)＝ax2＋2x＋1,若f(f(x))≥0在R上都恒成立,则实数a的取值范围为________.

点评本题是一个二次函数与复合函数的问题,具有一定的难度,解答时应注意内函数的值域就是外函数的定义域.

总之,高考对二次函数的考查一般不会单独命题,而是隐藏在函数的综合题中,在解答这类问题时,需特别注意数学思想的合理运用.

(完)