作图无定法 要旨系得法
——以网格作图中的轴对称为例
2022-10-25雷改良
雷改良
(湖北省武汉经济技术开发区第二中学,430056)
近几年中考网格作图经常出现轴对称的影子.相较于网格作图中的作分点、作垂线、作平移、作角平分线而言,网格中的作对称要稍微难一点.很多问题不是直接要我们作对称,而是将对称性的作图意图杂糅在颇为棘手的看似与对称无关的问题里面,导致学生对作图的核心把握不准,更不能将平时提炼的基本模型直接运用到该问题上.本文分类例说如何利用作对称的常用策略解决网格的有关经典作图问题.
一、作对称的常用策略
策略1利用轴对称性质直接作对称
例1如图1~图3,作点A关于MN的对称点.

基本方法对称轴是任何一对对称点所连线段的垂直平分线.
分析先过点A作对称轴的垂线,垂足是格点(如图1~图2),则直接倍长.若垂足不是格点,则可想办法构造中位线模型,如图3,连结AM并将其倍长至点C,再过C作对称轴MN的平行线交对称轴的垂线于一点B即为所求.
例2如图4,∆ABC是边长为1正方形网格中的格点三角形.
(1)画点A关于BC的对称点D;
(2)连结AD交BC于E点,画点E关于AC的对称点F.
分析(1)过点A作对称轴BC的垂线,垂足不是格点,则先将AB倍长至点M,再过点M作对称轴BC的平行线交对称轴的垂线于点D即为所求.
(2)因为点E为非格点,且∠BAC=45°,则可利用后面的策略3,构造∆ACH与∆ACB全等,再作CH边上的高AF,即可得点E关于AC的对称点F.

策略2利用对称轴作对称
例3(2020年武汉中考题)在8×5的网格中建立如图5的平面直角坐标系,四边形OABC的顶点坐标分别为O(0,0),A(3,4),B(8,4),C(5,0).仅用无刻度的直尺在给定网格中按下列步骤完成画图,并回答问题:
(1)将线段CB绕点C逆时针旋转90°,画出对应线段CD;
(2)在线段AB上画点E,使∠BCE=45°(保留画图过程的痕迹);
(3)连结AC,画点E关于直线AC的对称点F,并简要说明画法.
基本方法轴对称图形两对对称点交叉相连的交点在对称轴上.
分析第(1)、(2)问如图6.第(3)问,因为四边形ABCD是菱形,则对角线AC为对称轴,且点O与点B关于AC对称,连结OE与对称轴AC交于点M,连结BM并延长与AO的交点即为所求的对称点F(如图7).

策略3利用全等作对称
例4图8是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.∆ABC的顶点在格点上,仅用无刻度尺的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤画出BC关于AC对称的线段CD.
基本方法由点或线段所在三角形的对称图形,得到相应的对称点或对称边.
分析易知∠BAC=45°.如图8,构造∆ACD与∆ACB全等,即可得CB关于AC对称的线段CD.

例5如图9,∆ABC是边长为1正方形网格中的格点三角形.
(1)画∆ABC的角平分线BF;
(2)画点A关于BF的对称点G.
分析(1)利用三角形三个角平分线交于一点的性质.如图9,作出∠BAC和∠ACB的角平分线的交点E,连结BE并延长交AC于点F,BF即为∆ABC的角平分线.

二、常用策略应用
类型1利用对称求最值
例6如图10,在CD上确定一点P,使PA+PB的值最小.
分析本题求最值,本质则是作对称.如图10,利用策略1,找到点A关于CD的对称点E,连结BE交CD于点P即为所求.

类型2利用对称作角相等
例7(2019年武汉中考题改编)图11是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形ABCD的顶点在格点上,请选择适当的格点,用无刻度的直尺在边AB上画一点G,使∠AGD=∠BGC.(保留连线的痕迹,不要求说明理由)
分析要找到满足条件的点G,使∠AGD=∠BGC,可利用策略1.如图11,作D点关于AB的对称点E,连结CE交AB于点G即为所求.
类型3利用对称作线段相等
例8如图12,∆ABC中,AB=AC,B,C为格点.
(1)P为边AB上一点,用无刻度直尺在AC上找一点Q,使AQ=AP;
(2)M为BC上任意一点,在BC上找一点N,使CN=BM.

分析(1)此问可利用策略2解决.如图12(1),连结CP交对称轴于点D,连结BD并延长与AC的交点Q即为所求.
(2)可仿照问题(1),先在AC上取点E,在AB上找到点E关于对称轴的对称点F,再连结ME,与对称轴交于点H,连结FH并延长与BC的交点即为N(如图12(2)).
类型4利用对称作全等
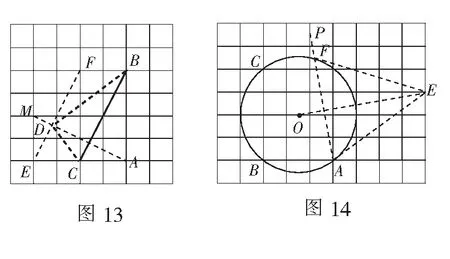
例9如图13,点A,B,C都在格点上,仅用无刻度的直尺,将∆ABC沿BC边翻折,画出翻折后的∆DBC.
分析要求画出翻折后的三角形,其核心是找到点A关于BC的对称点D,可利用策略1解决.如图13,先倍长AC到点E,作EF∥CB,再作BC的垂线AM,则AM与EF的交点即为点D.
类型5利用对称作切线
例10图14是由小正方形组成的9×7网格,每个小正方形的顶点叫做格点,A,B,C三个格点都在圆上.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
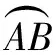
(2)画出格点E,使EA为⊙O的一条切线,并画出过点E的另一条切线EF,切点为F.
分析(1)略.(2)如图14,要求画出过点E的另一条切线EF,其核心就是作点A关于OE的对称点.因为OE所在直线是圆O的对称轴,只需要利用策略1,过点A作OE的垂线并延长,与圆O的交点即为点F.(因为OE为横5.5竖1的直角三角形的斜边,导致很多学生没有想到过点A作横1竖5.5的直角三角形的斜边与OE垂直.)
三、结束语
网格作图题灵活多变、丰富多彩,平面几何中很多问题都能借助网格来呈现.网格自身具有的几何特征和数值特征,使图形的一般几何性质得以特殊化和数量化.因此,网格作图为学生发现问题、分析问题、解决问题提供了多角度探究的空间.网格作图不仅能提高学生的识图和作图能力,还能多维度地培养学生的分析推理能力、计算能力、几何直观能力以及综合运用知识解决问题的能力.
初中数学中的尺规作图操作方法多种多样,教学中往往只注重操作方法,缺少对作图依据的合理阐释,这样会让学生知其然而不知其所以然,一旦遇到新问题仍是束手无策.网格作图问题其本质和常规尺规作图相同,作图原理并没有发生改变,只是采用的作图工具由直尺圆规变成了网格和无刻度的直尺,相当于是问题的载体发生了变化,因此在课堂教学中我们应更注重知识的生成过程,梳理相关内容的逻辑,帮助学生构建完善的知识体系,这样才能有助于学生在应用知识时进行知识的正迁移.
《义务教育数学课程标准(2011年版)》指出,核心素养反映的是数学本质和数学思想,是在数学学习过程中形成的,具有综合性、整体性和持久性.这就要求教师在课堂教学中不能按部就班地教学生获得问题的答案,而应启发学生挖掘问题内涵,让学生去主动思考解决这个问题应该使用哪些学过的数学知识及数学思想方法.教师只有在平时教学中渗透这样的数学思想方法,才能真正提高学生的数学核心素养.
