立足几何建模 领悟构造思想

刘 震

(浙江省杭州银湖实验中学,311422)

数学模型在初中数学教学与解题中扮演着非常重要的角色,特别是在几何部分,通过构造数学模型,常常可以将抽象问题直观化,复杂问题简单化.本文介绍“手拉手”模型,并运用“手拉手”模型解决近年来中考数学中的一系列热点难点问题,旨在深挖模型构造依据,感悟数学建模思想,培养学生的数学核心素养.

一、模型预备

1.“手拉手”全等

如图1,已知∆ABC和∆ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,连结BD,CE,则∆ABD≌∆ACE.

此模型具有三个特征:共顶点、双等腰、顶角相等.

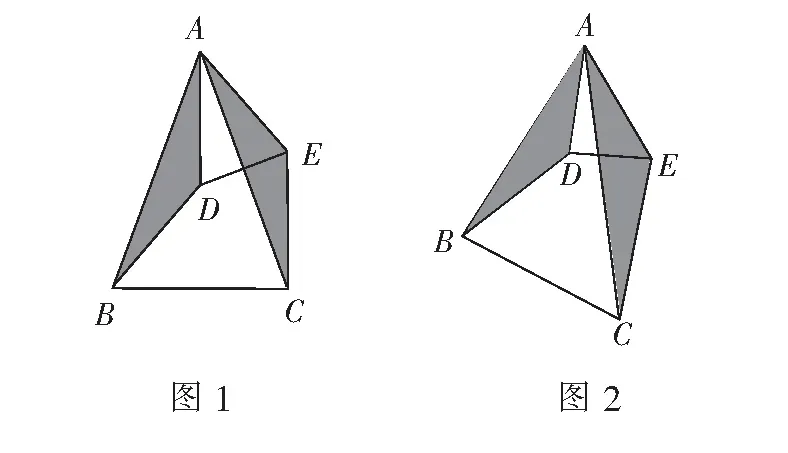
2.“手拉手”相似

如图2,已知∆ABC∽∆ADE,连结BD,CE,则∆ABD∽∆ACE.

此模型具有三个特征:共顶点且共顶点的两对对应边成比例、顶角相等.

二、模型应用

1.求线段长度

例1(2014年武汉中考题)如图3,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为______.

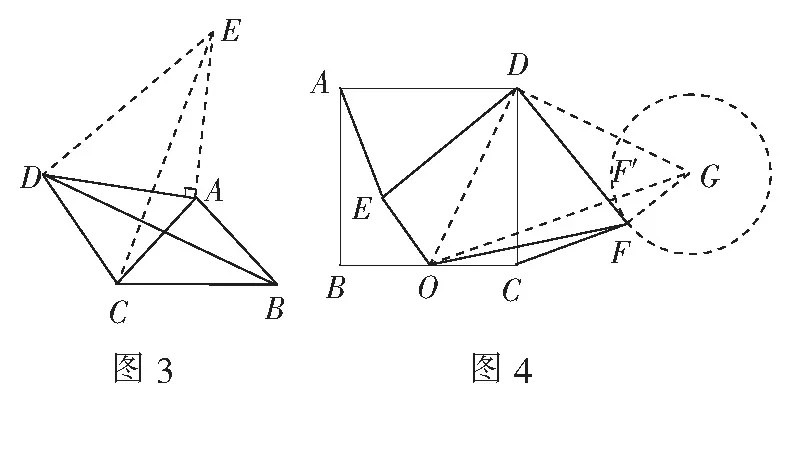
2.求线段最值

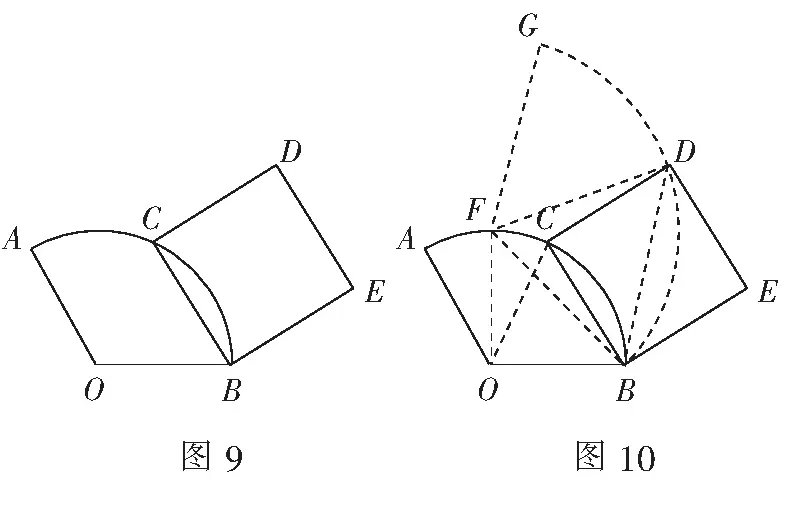
(1)求证:AE=CF;

(2)若A,E,O三点共线,连结OF,求线段OF的长；

(3)求线段OF长的最小值.

解析(1)由“手拉手”全等模型,易得∆ADE≌∆CDF,所以AE=CF.

(2)略.

(3)如图4,连结OD,将线段OD绕点D逆时针旋转90°得GD,连结OG,FG.同样,由“手拉手”全等模型,易得∆GDF≌∆ODE,所以GF=OE=2.

3.判定线段的数量关系

(1)求证:BD是该外接圆的直径;

(3)若∆ABC关于直线AB的对称图形为∆ABM,连结DM,试探究DM2,AM2,BM2三者之间满足的等量关系,并证明你的结论.

解析(1)略.

4.求面积最值

例4如图7,在四边形ABCD中,AD=2,CD=4.若∆ABC为正三角形,则∆BCD面积的最大值为______,最小值为______.

解析如图8,以CD为边向形内作正∆CDE,连结BE.因为∆ABC也为正三角形,由“手拉手”全等模型,易得∆BCE≌∆ACD,所以BE=AD=2.

因为∆CDE位置确定,所以点E为定点,由圆的定义可知,动点B在以E为圆心,2为半径的⊙E上运动.

5.求动点路径长

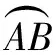
三、教学反思

1.分析条件特征,挖掘构造依据

通过构造“手拉手”模型,我们解决了初中几何中多种类型难题.那么上述问题为什么都可以构造“手拉手”模型呢?我们不难发现,这类题目中都存在着特殊几何图形——“等腰三角形”“等腰直角三角形”“等边三角形”,它们自身的几何性质为构造“手拉手”模型提供了方便.这样的例子有很多,如“中点”.当遇到中点时,我们应从哪些方面进行思考,进而构造出对应的模型呢?可以通过分析条件特征,挖掘模型构造依据:(1)已知一个中点,联系条件看是否为“等腰三角形三线合一”还是“直角三角形斜边上的中线等于斜边的一半”.普通三角形中线可考虑“倍长中线”,有时也可考虑过中点作平行线或再取中点构造中位线以挖掘出隐含中点;(2)已知两个中点,多为三角形中位线,若是两中点不在一个三角形中,可考虑再构造一个中点,将分散条件集中,化隐性为显性.

2.重视阅读能力,培养核心素养

很多学生在阅读题目之后没有头绪,缺乏思路,甚至出现理解错误.究其原因，一方面是因为几何模型的综合,有时并不会完整地展现几何模型,而只会展现模型中最基础的、关键的非连续文本或片段.这就需要我们掌握一定的非连续性文本阅读策略以提高数学阅读能力,进而能准确快速地捕捉到这些关键字眼或图表信息,找到显性或隐性的已知条件,并能在大脑中反应出可能的基本几何模型,进而选出正确的做法;另一方面是因为学生的推理能力不足,逻辑思维混乱,对模型的条件、结论及推理过程不熟,也就是对图形的数学本质没有深入的认识和理解.因此,在解题教学中,教师应注重对试题的本质属性,图形的数学本质进行钻研和挖掘,让学生清楚知识的来龙去脉.只有这样才能发展学生的合情推理、演绎推理能力和理性精神,培养他们的数学抽象、数学建模和直观想象等核心素养,养成良好的数学学习品质.

3.立足几何建模,领悟构造思想

数学建模就是根据实际问题来建立数学模型,并对数学模型进行求解,然后根据结果去解决实际问题.而数学建模思想其实是数学思想方法中的“构造法”.所谓“构造法”，就是指结合题目条件,在对条件进行深入分析的基础上,通过数学想象构建出一个合适的数学模型,从而辅助数学解题的方法.初中数学中的很多问题都可以模型化,但在构造模型时,一要明确构造的目的, 即为什么目的而构造(对问题进行转化化归,化抽象为具体,化繁为简,化难为易);二要弄清问题的特点,以便依据特点,确定方案、实现构造.正如匈牙利数学家路沙·彼得在其名著《无穷的玩艺:数学的探索与旅行》中所指出的:数学家们往往不是对问题进行正面攻击,而是不断将它构造、变形,直至把它转化成能够得到解决的问题.