基于教材理解 积累活动经验
——对一道九年级期末试题的思考
2022-10-25钟晓红
钟晓红
(广东省中山市永宁中学,528415)
教材是数学教学的依据,因此教师如何合理、灵活地处理好教材,是当前深化课堂教学改革的重要环节.本文以2021-2022学年广东省中山市九年级(上)期末试卷第17题为例,通过解读试题,引发对教材中“综合与实践”教学的思考,与同行交流.
一、试题呈现
如图1,将半径为1、圆心角为60°的扇形纸片AOB,在直线l上向右作无滑动的滚动至扇形A′O′B′处,则顶点O经过的路线总长为______.

二、试题评价
《义务教育数学课程标准(2011年版)》指出:“综合与实践”是积累数学活动经验的重要载体.教学中注重结合具体的学习内容,设计有效的数学探究活动,使学生经历数学的发生发展过程,是学生积累数学活动经验的重要途径[1].本题以图形滚动为背景,以操作探究问题呈现,凸显对学生直观想象、数学建模和数学运算等核心素养的考查.
1.源于教材
本题源于人教版教材九年级上册第118页数学活动1“车轮做成圆形的数学道理”,蕴含丰富的数学知识和极强的趣味性.题目涉及旋转的定义与性质、扇形的弧长公式、圆的概念与切线的性质等基础知识,考查了学生操作、几何直观、推理计算、应用意识等素养.
2.活于教材
在图形滚动的过程中,构成图形要素(点、线等)也随之运动.通过探求特殊点的运动轨迹,从而得到某个点经过的路线总长.解题时,把扇形的弧长计算与运动轨迹问题结合起来,把动态问题转化为静态问题,体现了数形结合、模型、分类讨论、运动与静止等数学思想方法,从而获得研究问题的活动经验,培养学生分析问题和空间想象的能力.
三、试题解析及难点分析
如图2所示,顶点O经过的路线可以分成三部分:
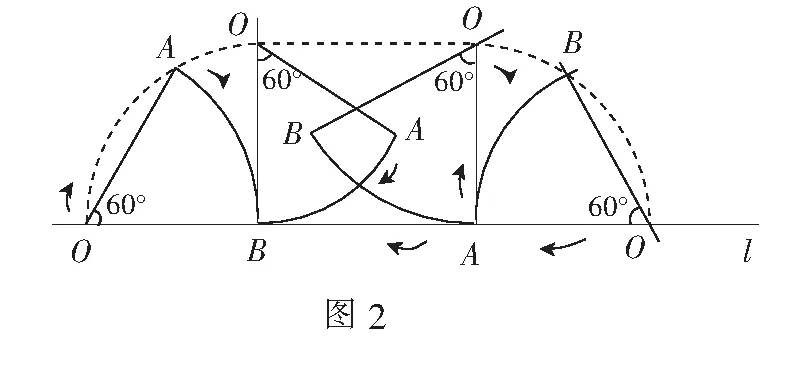
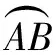
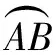
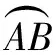
难点1结合“扇形AOB在直线l上向右作无滑动的滚动至扇形A′O′B′处”的文字和图形语言,可以理解为“扇形AOB在直线l上向右作无滑动的滚动一周”;
难点2学生虽然能理解“无滑动的滚动一周”的含义,但缺乏“无滑动的滚动一周”的活动经验,对其操作含糊不清;
难点3大部分学生对求动点运动轨迹的基本方法摸不着头脑,不知道如何寻找动点在运动过程中保持不变的性质.如图3,可以看到扇形AOB在运动中有(1)~(4)的四个状态,点O有三个运动轨迹过程,为什么要讨论(1)~(4)的四个状态,学生缺乏思考;
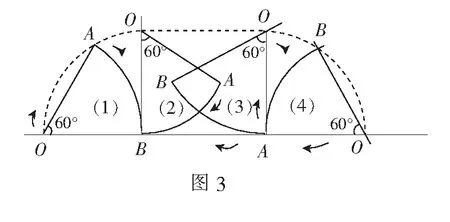
难点4出现知识盲区,从状态(2)到状态(3),点O到直线l的距离始终保持不变,这个距离为扇形AOB(圆O)的半径,为什么此时点O的运动轨迹为平行于直线l的线段?
四、教学实践
1.探究活动,感受难点
活动用“半径为1、圆心角为60°”的扇形纸片AOB,在直线l上向右作无滑动的滚动一周.
问题1用笔画出点O的运动路线.
设计意图让学生通过动手操作的活动,猜测、观察点O所形成的轨迹过程,领悟数学的基础知识和基本技能,积累基本活动经验,从而发展学生的实践能力,感受数学来源于生活,激发学生学习数学的兴趣.
2.从特殊到一般,化解难点
问题2如图4,在直线l上线段BO绕着点B按顺时针方向旋转一定角度到线段BO′的位置,点O到点O′的轨迹是什么形状?点O运动的路径长是多少?

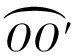
问题3如图5,圆O在直线l上向右作无滑动的滚动一周到圆O′,点O到点O′的轨迹是什么形状?圆心O运动的路径长是多少?
设计意图我们知道“圆上各点到圆心的距离都等于半径”,那么圆O上的特殊点是圆心O与直线l相切的切点A,连结OA,有OA⊥l,从而把点O的运动轨迹转化为点A的运动轨迹,由OO′∥AA′且OO′=AA′,推断出点O的运动轨迹为平行于直线l的线段OO′,该线段长为AA′等于圆O的周长,进而发现圆心的运动路径长与图形的周长有关.在这实验操作中,学生对圆的滚动有了进一步认识,提出“车轮做成圆形的数学道理”,帮助学生建立数学与生活间的联系,积累了生活经验,获得了知识体验.
问题4(2021-2022学年中山市九年级(上)期末试卷第17题)详见文首,此处从略.
设计意图通过问题1、2、3的铺垫,问题4本质是对问题2和3的综合运用,学生对点O经过的路线分成三部分有了更深刻的理解.在探求点O的运动轨迹过程中,学生了解到动点轨迹有圆弧型、直线型;解题过程中,学生体会了运动变化思想、特殊化思想、分类讨论思想、化归思想.这些都有助于学生将活动经验转化为思想方法,形成解题技巧,提高解题能力.
3.变式训练,发散思维
变式1如图6,将边长为1的等边∆AOB,在直线l上向右作无滑动的滚动一周,则点O经过的路线总长为______.

变式2如图7,将边长为1的正方形OABC,在直线l上向右作无滑动的滚动一周,则点O经过的路线总长为______.
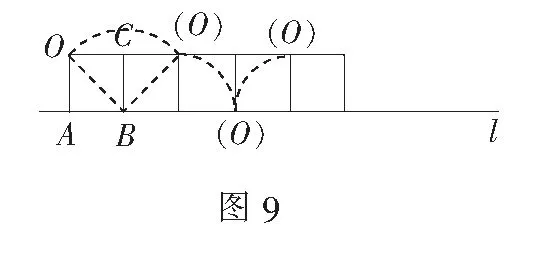
设计意图如图8、9所示,通过变式1和2,类比其他几何图形在直线上滚动的情况,了解它们之间的联系与区别,帮助学生积累解决这类问题的模型和方法,起到触类旁通的作用.

四、教学启示
1.立足教材,夯实基础
《义务教育数学课程标准(2011年版)》强调:教材是实施数学教学的重要资源[1].人教版初中数学教材在章引言、阅读与思考、数学活动、信息技术应用、实验与探究等学习素材提供了丰富的与学生生活相联系的“综合与实践”资源,学生通过观察、实验、猜测、推理、交流、反思等,感悟知识的形成和应用,促进学生创新意识和实践能力的发展.因此,在平时教学中,教师不仅让学生了解知识背景,还要理解知识形成过程,从而揭示知识间的联系.
2.动手操作,积累经验
“纸上得来终觉浅,绝知此事要躬行.”数学活动“车轮做成圆形的数学道理”属于“综合与实践”的内容,在教学中教师引导学生动手操作与实践,最终达成学生从“学数学”到“做数学”的转变,培养学生综合运用所学知识(圆的概念与切线的性质)与方法解决实际问题;培养学生的问题意识、应用意识和创新意识,积累活动经验,提高学生解决现实问题的能力.
3.注重思想,提升素养
数学思想方法的形成是一项长期的任务,应该落实在每一堂数学课上.如本文中的教学实践利用数学知识形成过程,从线段、圆到扇形再到等边三角形、正方形等规则图形来发现几何图形滚动问题的规律,渗透运动变化和从特殊到一般的思想;扇形AOB的顶点O经过的路线需要分成三部分来解释,应用了分类思想;通过动手操作画出动点的运动路线求点的路径长,体现数形结合思想.数学思想方法需要“悟”[2],因此教师通过创设恰当的问题情境,让学生亲身经历学习过程,从而真正地理解知识,提升学生解决问题的素养.
