特殊到一般 具体到抽象
——以一道几何探究题为例
2022-10-25何伟
何 伟
(上海外国语大学苏河湾实验中学,200071)
数学学习来源于解决问题的过程,解题需要的是思维能力和数学方法.对探究性问题的深入思考和不断尝试,能够帮助学生更好地完善知识体系、提升思维能力、彻底理解数学思想方法,最终形成良好的认知结构和解决问题的核心能力.本文从一道几何探究题入手,阐述如何在探究过程中,体现由特殊到一般、由具体到抽象的数学方法.
一、问题提出
由小正方形组成的长方形的对角线所穿越的小正方形个数研究:
不难发现,由6×2个小正方形组成的长方形,它的对角线穿过6个小正方形(如图1).由7×5个小正方形组成的长方形,它的对角线穿过11个小正方形(如图2).

问题(1)由2022×120个小正方形组成的长方形,它的对角线穿过多少个小正方形?
(2)能否给出由m×n个(其中m,n是正整数)小正方形组成的长方形,它的对角线穿过的小正方形个数的计算公式,并说明理由.
(3)能否将上述结论推广成由m×n×h(其中m,n,h是正整数)个小立方体组成的长方体,它的对角线穿过的小立方体的个数?
二、问题分析
长方形由m×n个(其中m,n是正整数)小正方形组成,如何来计算它的对角线穿过的小正方形数量呢?
从特殊情况入手:
1.m=n(如图3~图4);

2.gcd(m,n)=1(如图5~图6);
3.gcd(m,n)>1(图7~图8),其中gcd(m,n)表示m,n的最大公约数.

对三种情况进行研究,可得f(对角线穿过的小正方形数量)与m,n的关系(见表1).

表1
由表1,可提出如下猜想:长方形由m×n个(其中m,n是正整数)小正方形组成,它的对角线穿过的小正方形数量f=m+n-gcd(m,n).
三、结论验证


(2)对角线与m+1条竖直线有m+1个交点,与n+1条水平线有n+1个交点,由于对角线的两个端点被重复计算,所以对角线与所有格线共有(m+1)+(n+1)-2=m+n个交点,且除去两端端点外,其余的交点坐标(a,b)中有且只有一个数值为整数,0≤a≤m,0≤b≤n.
(3)这m+n个交点将对角线分为(m+n-1)段,每一小段都与穿越它的小方格一一对应,所以对角线共穿过了(m+n-1)个小方格,即满足猜想公式f=m+n-gcd(m,n),此时gcd(m,n)=1.


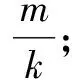
综上所述,长方形由m×n个(其中m,n是正整数)小正方形组成,其对角线穿过的小正方形数量f=m+n-gcd(m,n),无论m与n的数量关系如何均满足此公式.
四、问题解决
对于问题(1),因为gcd(2022,120)=6,所以由2022×120个小正方形组成的长方形,它的对角线穿过的小正方形数量f=m+n-gcd(m,n)=2022+120-6=2136.
五、特殊问题一般化、具体问题抽象化
接下来,我们将上述结论推广到由m×n×h(其中m,n,h是正整数)个小立方体组成的长方体中,它的对角线穿过的小立方体的个数.
在平面十字坐标系中,笔者在解决“由m×n个(其中m,n是正整数)小正方形组成的长方形中,它的对角线穿过的小正方形个数的计算公式”是通过计算对角线分别与横格线、竖格线的交点数,来计算对角线的分段数,从而找出所穿越的小方格数量,得出f=m+n-gcd(m,n)的结论.
经分析,不难发现公式f=m+n-gcd(m,n)形似容斥原理公式,即对于长方形的对角线每穿越一次纵、横格线时产生一个交点,其在十字坐标系内坐标为(a,b),0≤a≤m,0≤b≤n,a,b中至少有一个数值为整数,这些交点将对角线分段,分段数为f(m∪n)=m+n-m∩n(如图11).

而在立体三维坐标系中,想象由m×n×h(其中,m,n,h是正整数)个小立方体组成的长方体中,体对角线所穿越的将是内部小立方体的顶点、棱和面.由前文中的平面体系证明,不难发现如下结论:
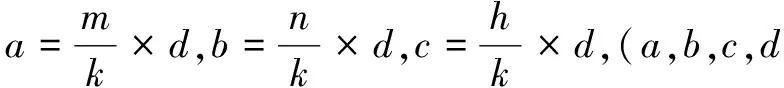
2.当体对角线穿越内部小立方体棱上某点(棱两端端点除外)的时候,必有棱所交界的两个方向产生大于1的最大公约数的整数倍,即坐标(a,b,c)中必有2个数值为整数,此时体对角线可穿越2个数值为整数值的坐标点后进入一个新小立方体.
3.当体对角线穿越内部小立方体面上某点(四周棱上点除外)的时候,必有点的坐标(a,b,c)中有且只有1个数值为整数,而且每穿过一个面,就可以到达一个新的小立方体.
例如,由 9×5×6个小立方体组成的长方体,其三视图如图12所示.

因为gcd(9,5,6)=1,所以体对角线没有直接穿越小立方体顶点;
因为gcd(9,6)=3,所以在m-h构成的正视图中,体对角线在长方体内部2次穿越小立方体的棱(不包括两端端点);
因为gcd(9,5)=1,gcd(5,6)=1,所以在m-n构成的俯视图、n-h构成的侧视图中体对角线无穿越内部小立方体棱,均穿越面到达新的小立方体.
经过作图计数得到体对角线穿越小立方体数量是:
9+5+6-gcd(9,6)-gcd(9,5)-gcd(5,6)+gcd(9,5,6)=16(个)
由上分析,可以将问题转化为体对角线在立体坐标系中与小立方体面、棱、顶点的所有交点坐标(a,b,c),已知0≤a≤m,0≤b≤n,0≤c≤h,至少有一个数值为整数,即可计入穿越一个新的立方体.
因此,由m×n×h(其中m,n,h是正整数)个小立方体组成的长方体,它的体对角线穿过小立方体个数F的计数公式为:
F=m+n+h-gcd(m,n)-gcd(m,h)-gcd(n,h)+gcd(m,n,h).
同样,上述公式也形似容斥原理公式m+n+h-m∩n-m∩h-n∩h+m∩n∩h.
六、反思
问题(1)中给出具体的行和列的数字,计算出对角线穿过的正方形,便于上手解决该问题,通过一般化、具体化的问题,找出相同点和不同点,从而推导出公式;问题(2)递进到一般化的m×n个(其中m,n是正整数)小正方形组成的长方形中,它的对角线穿过的小正方形个数的计算公式,需要找出行列数互素以及不互素情况下如何用一个公式来表示;问题(3)更进一步,从平面上升到立体,需要推导出长方体对角线穿过的正方体个数的公式.该探究题由具体数字到抽象字母,从平面图形到立体图形的延伸,开阔了学生的视野,激发了学生的数学思维.
