考虑柱塞两种姿态的柱塞副燃油泄漏研究
2022-08-25张勇李攀高振波王丹丹
张勇,李攀,高振波,王丹丹
(华南理工大学机械与汽车工程学院,广东 广州 510640)
高压共轨喷油技术是实现发动机节能减排的关键技术之一,相比传统供油系统而言,其工作可靠性和工作效率有较大提高。但高压共轨喷油技术中柱塞副的密封性能较低,存在泄漏问题,导致喷油器响应缓慢且喷油雾化效果差,使发动机效率降低、尾气污染物排放增加。
目前针对柱塞副的泄漏问题已有许多研究成果。石蜡燃料相比于传统燃料不含芳香烃成分且密度低,采用该燃料可以减少柱塞副等部件磨损。Carmen Mata等研究了水柱塞泵中各个参数对柱塞副间隙泄漏速率的影响,为基于水介质的柱塞泵的设计提供了依据。江权等研究柱塞泵缸体的衬套,发现衬套厚度越大,柱塞副泄漏越严重。由于柱塞副间隙大小与表面粗糙度是同一个数量级别,因此柱塞和柱塞套表面形貌特征对柱塞副的泄漏也有很大影响。另外,在针阀外径面上加工环形槽可以降低针阀副的间隙燃油泄漏速率,在柱塞泵柱塞副中应用环形槽可以改善柱塞的微运动轨迹。
目前很少有针对高压共轨喷油器柱塞副在柱塞倾斜和偏心状态下泄漏情况的研究,鉴于此,本研究建立了柱塞副间隙流动的雷诺方程、油膜厚度方程和油膜截面速度方程,并采用数值分析的方法对柱塞倾斜和偏心状态下的柱塞副泄漏情况进行研究。
1 数学模型
1.1 雷诺方程
油膜雷诺方程的推导基于以下假设: a)由于柱塞副间隙油膜厚度很小,所以油膜压力和速度在其厚度方向上的变化可以忽略,且间隙燃油的流动为层流流动;b)不计柱塞的旋转;c)忽略油膜的惯性力和体积力的作用,柱塞副表面无滑移。
为便于计算,将柱塞副环形油膜展开为平面,如图1所示。=[0,2π]为油膜圆周方向,为柱塞半径;为油膜厚度方向,=0表示接触柱塞套,=表示接触柱塞;=[0,]为油膜轴向,为油膜长度,=0表示进口,=表示出口。

图1 柱塞副间隙油膜展开平面
因此,动量方程可以简化为

(1)


(2)


(3)
把式(2)代入式(3)可得柱塞副静态油膜雷诺方程:

(4)
式中:为油膜厚度;为油膜压力;,分别为燃油密度和动力黏度;,,分别为坐标轴,,的速度分量;为柱塞轴向运动速度。
雷诺方程边界条件如下。
压力进口边界条件:
=;
(5)
压力出口边界条件:
=0.1 MPa;
(6)
周期性边界条件:
(0,)=(2π,)。
(7)
1.2 非等温流动方程
在静态条件下,由于油膜流动过程压力下降,导致轴向温度升高,使间隙内油膜流动非等温。因此,可以用能量守恒理论分析温升与压降之间的关系:

(8)
式中:为油膜比热容;为油膜温度;为柱塞副进口温度。
1.3 柱塞副油膜厚度方程
1.3.1 不考虑柱塞副变形
1) 偏心状态
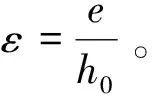

图2 柱塞在柱塞套内偏心状态
令∠=,使平行于,且垂直于,由于>≫,所以∠=∠=d≈0。因为=+-,且cosd≈1,得出:

(9)
柱塞在柱塞套内偏心,则任意一点的油膜厚度为

(10)
2) 倾斜状态
当柱塞与柱塞套发生倾斜时(见图3),油膜厚度发生改变且设入口和出口偏移量相等。

图3 柱塞在柱塞套内倾斜状态
设柱塞的倾斜角度为,油膜长度为,可得柱塞在柱塞套内倾斜时任意一点的油膜厚度:

(11)
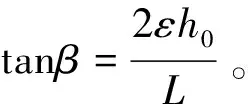
(12)
将式(12)代入式(13)得到倾斜条件下的油膜厚度方程:

(13)
1.3.2 考虑柱塞副变形
柱塞副变形的主要原因是弹性变形和热变形。对于弹性变形,可以根据 Lame公式计算厚壁筒,但该公式是基于该问题简化为平面问题计算而得,因此有较大误差,本研究对此做出修正,得到变形为

(14)
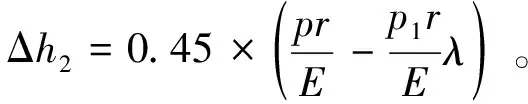
(15)
式中:Δ,Δ分别为柱塞套和柱塞的径向弹性形变;,分别为柱塞套和柱塞的泊松比;,分别为柱塞套和柱塞的弹性模量;,分别为柱塞套的外半径和内半径。
对于热变形,燃油热量传导至柱塞副,由于柱塞副内散热条件很差,所以在柱坐标(,,)下为热稳态。考虑导热系数为常数,则柱塞副温度与燃油温度之间的导热方程为
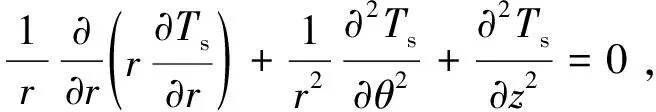
(16)
Δ=-。
(17)
根据热弹性理论,热膨胀所导致的变形为

(18)

(19)
式中:Δ,Δ分别为柱塞套和柱塞的热膨胀形变;,分别为柱塞套和柱塞的线膨胀系数;,,Δ分别为柱塞副的温度、初始温度和温差。
根据以上关系式,得出考虑变形的油膜厚度方程。
1) 偏心条件:

(20)
2) 倾斜条件:

(21)
1.4 油膜物性参数方程
燃油的物性参数是随着其温度和压力的变化而变化,同时燃油物性参数反过来会影响其压力和温度。所以为了更为精确地研究柱塞副的泄漏问题,考虑燃油物性参数是非常重要的。燃油在柱塞副间隙流动时会产生温升和压降,同时造成了其物性参数变化,根据 Cameron 等所提出的考虑压力和温度耦合作用的黏度的幂式方程,得到了密度和比热容随压力和温度的关系方程:
(,)=(+)(+)(+),
(22)
(,)=(+)(+)(+),
(23)
(,)=(+)(+)(+)。
(24)
式中:为温度;为压力;为黏度;为密度;为比热容。以上物性参数方程的系数见表1。

表1 公式(22)、 公式(23)和 公式(24)的系数
1.5 油膜截面速度方程
计算静态下间隙油膜泄漏速率的经典公式如下。
1) 同心状态下:
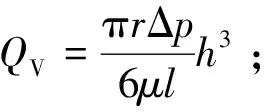
(25)
2) 偏心状态下:
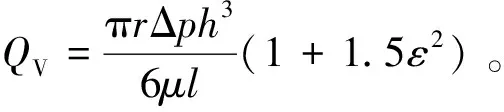
(26)
本研究以截面的速度方程来求解柱塞副的泄漏速率,由上面推导可知,静态下油膜的轴向速度为

(27)
因此柱塞副油膜泄漏速率为
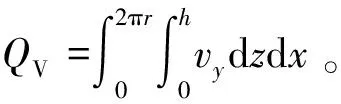
(28)
2 求解
2.1 离散化
式(5)油膜雷诺方程为椭圆形偏微分方程,需要进行数值计算求解,因此对方程离散化处理,将展开后的柱塞副油膜区域进行网格划分(见图4)。
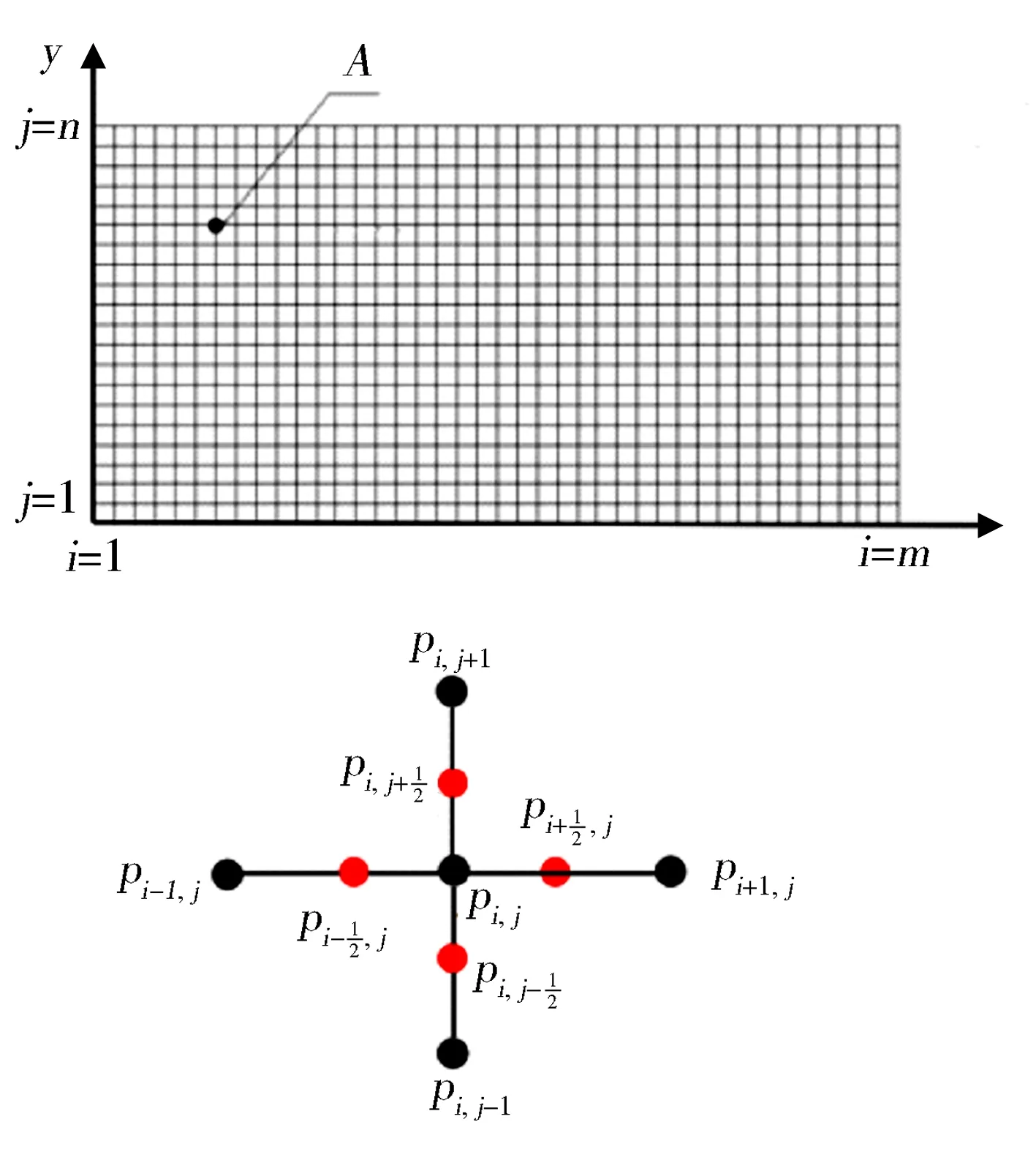
图4 油膜区域的离散化
得到油膜雷诺方程的差分格式:

(29)
式中:

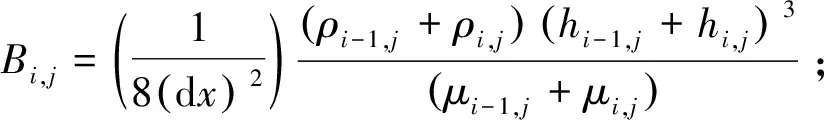


,=,+,+,+,。
对该截面速度方程进行离散化处理,在(,)截面上建立截面网格。在上面数值迭代中求出压力分布、黏度分布和膜厚分布。然后用压力差商近似截面的压力偏导,再对网格节点上对应的值代入即可,所以截面速度方程的差分格式为

(30)
式中:值代表截面所在位置。
求出截面所在的速度分布后,可得泄漏速率为

(31)
2.2 迭代计算
采用Jacobi 迭代方法(见图5)进行计算。首先,给定一个压力和温度的初始分布以及压力分布和温度分布边界条件,计算出初始的油膜厚度分布和油膜物性参数分布,然后对油膜雷诺方程进行迭代计算;计算出来的压力分布用来计算油膜的温度分布,再通过导热方程迭代计算柱塞副温度,最后计算油膜厚度分布。当迭代后的压力差值与迭代前的压力差值达到所设定的误差范围,则输出油膜压力分布、温度分布、厚度分布、物性参数分布和柱塞副油膜体积泄漏速率,计算结束;否则,继续计算,直至迭代前后的压力差值达到所设定误差。

图5 柱塞副间隙流场数值迭代程序
3 计算结果分析
3.1 数学模型验证
输入喷油器的主要结构参数(见表2),进行柱塞倾斜状态和柱塞偏心状态的数值计算迭代。为了验证数学模型的有效性,将模型计算和经典公式计算的柱塞副燃油泄漏速率数据以及试验值进行对比。

表2 模型输入主要参数
图6示出了不同柱塞状态、不同进口油压下泄漏速率的对比情况。

图6 不同进口油压下泄漏速率的对比
从图6中可以看出,偏心条件下经典公式计算的泄漏速率和本研究数学模型的计算数据具有相同的变化趋势,即燃油泄漏速率随着进口油压的增大而增大,且模型计算泄漏速率与经典公式的计算值相差很小;模型计算值与试验值相比存在一定误差,但不大,验证了数学模型的有效性。从图中还可以看出,对于同一进口油压,偏心条件下的柱塞副泄漏速率大于倾斜条件下的泄漏速率。
3.2 泄漏速率
通过截面速度方程计算出在偏心和倾斜状态下的柱塞副间隙燃油泄漏速率(见图7和图8)。
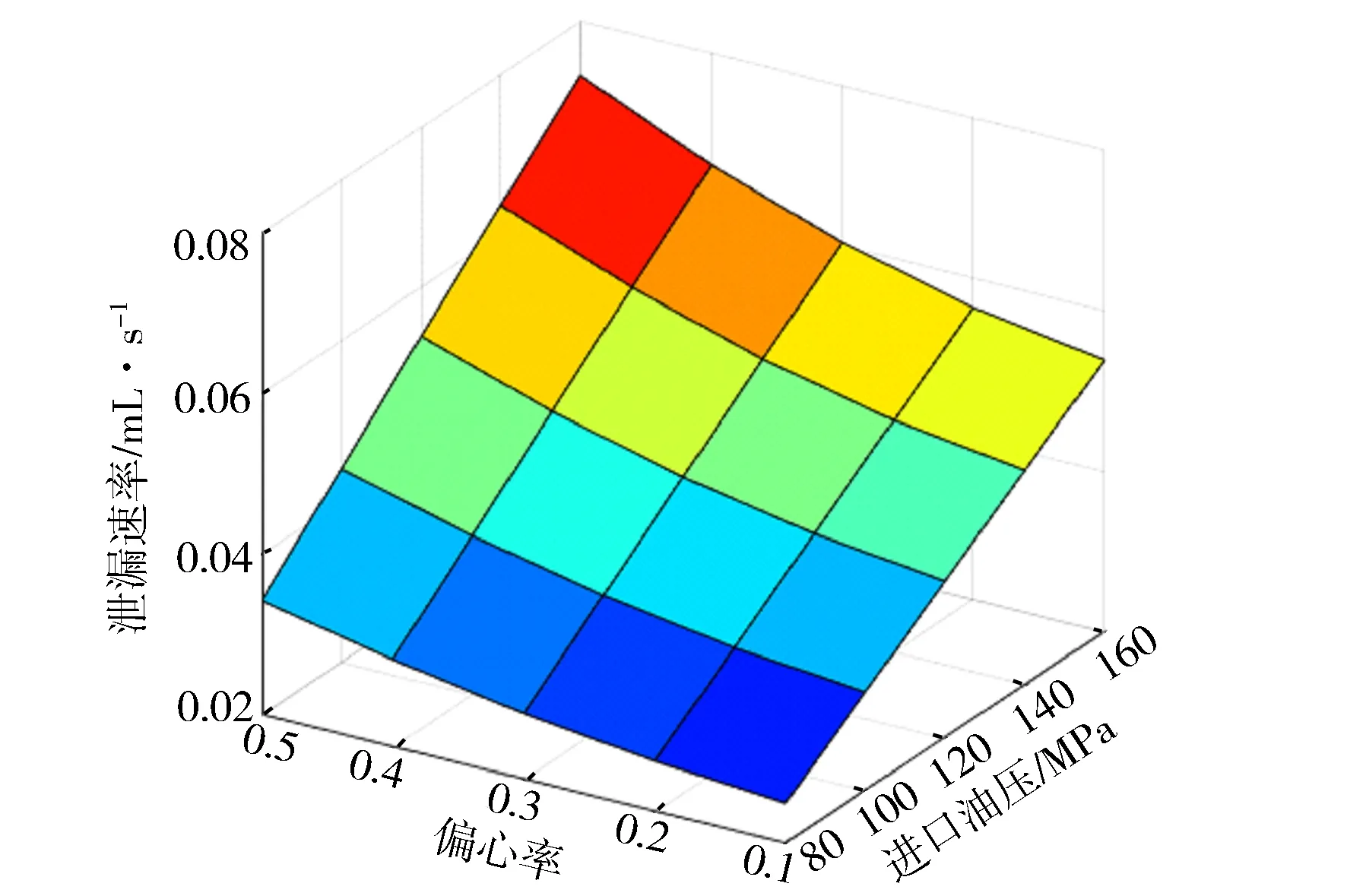
图7 偏心条件下的燃油泄漏速率变化

图8 倾斜条件下的燃油泄漏速率变化
从图7中可见,偏心状态下,燃油泄漏速率是随着柱塞偏心率的增大而增大,随着进口油压的增大而增大。进口油压为160 MPa,偏心率为0.5时,泄漏速率最大,为0.073 2 mL/s。从图8中可知,倾斜状态下,燃油泄漏速率随着柱塞倾斜角的增大而增大,但其泄漏速率增长率要小于偏心状态的增长率;燃油泄漏速率也随着进口油压的增大而增大,进口油压为160 MPa,倾斜角0.010 32°时,泄漏速率最大,为0.055 8 mL/s。
3.3 泄漏油膜厚度
计算得出进口油压为160 MPa时,柱塞在偏心和倾斜状态下的油膜厚度分布(见图9和图10)。从图中可以看出,从进口到出口,油膜厚度逐渐减小,这是由于进口压力大造成柱塞副在进口处变形大,而出口处主要是油膜温度高造成其膨胀。图9中的凹陷是因为柱塞偏心,图10中的凹陷和出口处的翘起是因为柱塞倾斜。本研究取油膜厚度分布中间处进行数据对比(见图11和图12),在偏心状态下油膜最小厚度随着偏心率增加而减小,而倾斜状态下油膜厚度在进口处随倾斜角增加而减小,但在出口处却增加。

图9 偏心条件下油膜厚度分布(偏心率0.5)

图10 倾斜条件下油膜厚度分布(倾斜角0.010 32°)

图11 不同偏心率下的油膜厚度变化

图12 不同倾斜角下的油膜厚度变化
3.4 泄漏油膜温度
图13和图14示出进口油压160 MPa时,柱塞偏心和倾斜状态下的油膜温度分布情况。从图中可知,油膜温度从进口到出口逐渐变高,且在出口处温度变化梯度大。在径向上,偏心状态下,在油膜薄时其温度较低,在油膜厚时温度较高;倾斜状态下,进口处的油膜薄时其温度较低,在油膜厚时温度较高,而出口处则相反。取中间处油膜的数据作比较(见图15和图16),可以看出,对于偏心状态,在进口处油膜温度随着偏心率变化其值变化不大,在出口处随偏心率增加而减小。在倾斜状态,油膜温度随倾斜角的增加而增加。

图13 偏心条件下油膜温度分布(偏心率0.5)

图14 倾斜条件下油膜温度分布(倾斜角0.010 32°)
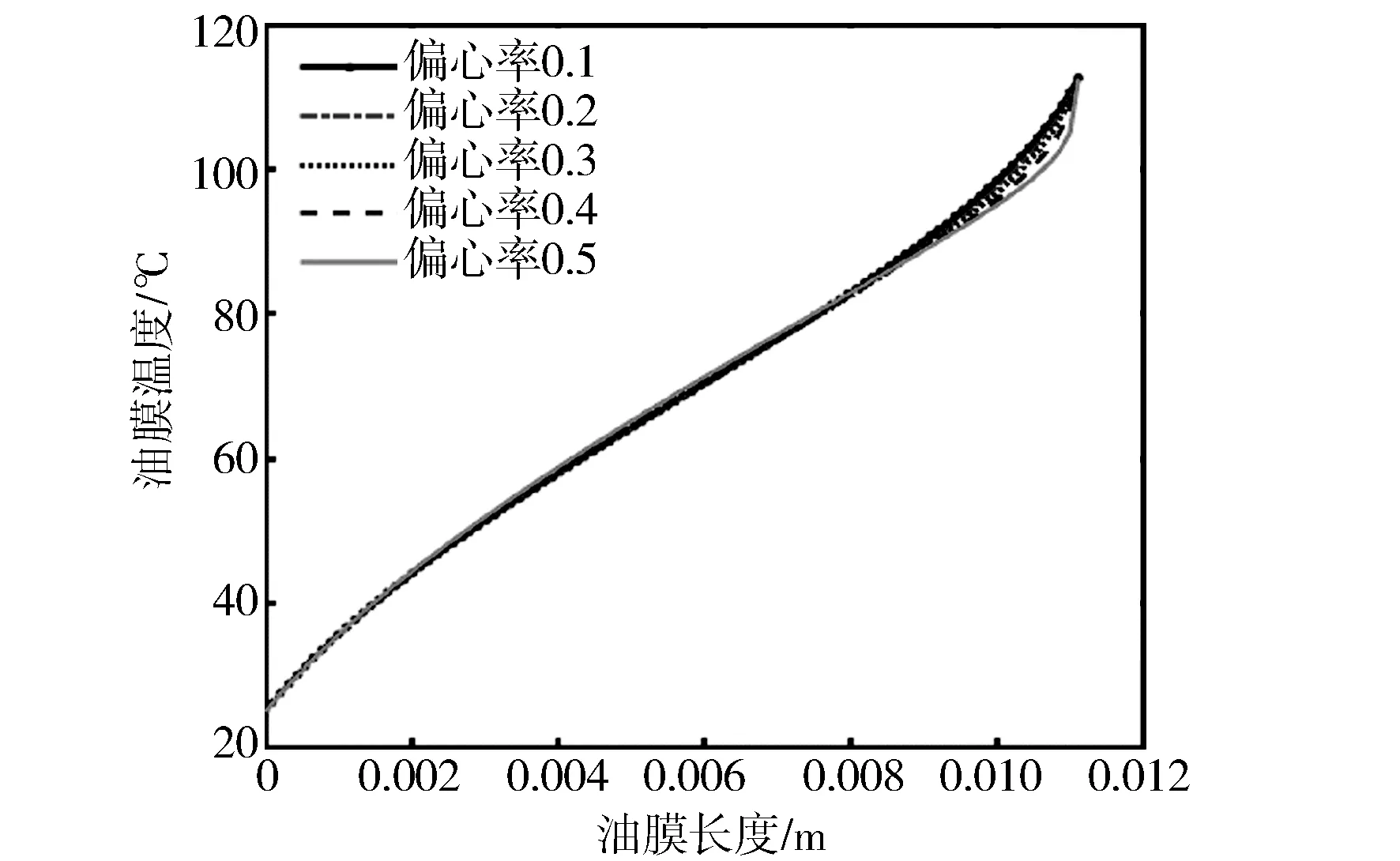
图15 不同偏心率下的油膜温度变化

图16 不同倾斜角下的油膜温度变化
3.5 泄漏油膜密度
计算得出进口油压160 MPa时的油膜密度分布(见图17和图18)。从图中可以看出,油膜密度从进口到出口逐渐降低,在出口处变化剧烈,这是由于出口处油膜厚度较薄造成的。在径向上,偏心状态下油膜密度在油膜较薄处较高,且在较厚处油膜密度较低;倾斜状态下,进口处的油膜薄时其密度较低,在油膜厚时油膜密度较高,而出口处则相反。图19和图20分别示出柱塞在偏心和倾斜状态下中间处的油膜密度数据对比。由图可见,在不同的偏心率下,油膜密度在进口处变化很小,在出口处偏心率越大其值越高;在倾斜状态下,油膜密度随倾斜角增加而减小。

图17 偏心条件下油膜密度分布(偏心率0.5)

图18 倾斜条件下油膜密度分布(倾斜角0.010 32°)
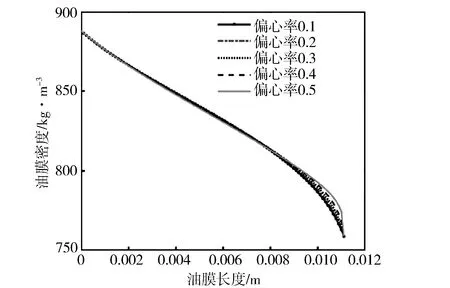
图19 不同偏心率下的油膜密度变化

图20 不同倾斜角下的油膜密度变化
4 结论
a) 在偏心和倾斜状态下,燃油泄漏速率是随着柱塞偏心率以及倾斜角的增大而增大,但偏心状态的泄漏速率要大于倾斜状态的泄漏速率,并且燃油泄漏速率是随着进口油压的增大而增大;
b) 从进口到出口,油膜厚度逐渐减小;最小油膜厚度随着偏心率增加而减小,在进口处油膜厚度随倾斜角增加而减小,但在出口处则相反;
c) 油膜温度从进口到出口逐渐变高;偏心状态下,在进口处油膜温度随着偏心率变化其值变化不大,在出口处随偏心率增加而减小;在倾斜状态,油膜温度随倾斜角的增加而增加;
d) 油膜密度从进口到出口逐渐降低;在不同的偏心率下,油膜密度在进口处变化很小,在出口处偏心率越大其值越高;在不同倾斜角度下,油膜密度随倾斜角增加而减小。
