核电循环泵齿轮箱强制喷射润滑仿真研究

李宏天 冯成程 董庆兵 魏 静 何 东

（1 太原重工股份有限公司， 山西 太原 030024）

（2 重庆大学 机械传动国家重点实验室， 重庆 400044）

（3 重庆大学 机械工程学院， 重庆 400044）

（4 重庆齿轮箱有限责任公司， 重庆 402263）

0 引言

核电的安全开发是国家综合实力的集中体现，核电站中的海水循环泵齿轮箱是核电机组的核心部件之一，对其设计、制造、装配等技术有着极高的要求。其中，润滑系统作为核电齿轮箱的关键装置，对提高摩擦副的耐磨性和设备可靠性、延长关键零部件的使用寿命、减少齿轮箱设备故障等有着重要作用。

流体动力学是一门涉及流体研究的学科[1]，随着算法与程序的不断改进以及计算机硬件的进步发展，计算流体动力学（Computational fluid dynamics，CFD）已经逐渐成为齿轮箱飞溅润滑研究的重要手段。目前，常见的CFD 算法主要包括有限体积法和粒子法[2]19-20。如果没有特定的网格处理技术，在预处理步骤中使用传统的有限体积法（Finite volume method，FVM）来生成高质量的非结构化网格将是非常耗时的，且一些复杂的表面仍然难以被正确地啮合。本文中所研究的行星齿轮箱内部结构复杂且体积较大，难以使用FVM 方法从内部复杂空间表面创建精确的网格跟踪流体流动。粒子法则不需要通过网格或标量进行显式表面跟踪，连续体被离散的粒子数离散，没有网格约束；每个粒子都相应地以自己的质量、密度、速度和施加在其身上的外部或内部力来移动[3]1-2。粒子法已被广泛应用于齿轮箱的润滑研究。

常用的粒子法[2]21-24包括光滑粒子流体力学法（Smooth particle hydrodynamic，SPH）、移动粒子半隐式法（Moving particle semi-implicit，MPS）和有限体积点法（Finite volume particle，FVP）。Groenenboom 等运用SPH 法与有限元耦合的方法对变速箱飞溅润滑进行了研究，结果表明，该方法在湍流和流固耦合模型上具有良好应用[4]。Ji 等采用多相SPH 公式解析复杂的多相流，对油面下的速度场和速度剖面进行了综合分析，数值计算结果与实验测速结果吻合较好[5]。Keller 等利用SPH 方法研究了油射流撞击旋转正齿轮过程中复杂的两相流，确定了倾角对润滑油的成膜、飞溅过程以及阻力转矩的影响[6]。SPH 方法遵循显式预测校正过程，其效率更高，但其精度和稳定性较低[7]421[8-9]。使用MPS 和FVP 方法进行CFD 模拟可能会花费更多的计算时间，但会产生更高精度的结果。

针对具有自由表面的不可压缩流动，Koshizuka等开发了MPS 方法，并利用该方法对高速铁路列车变速箱内润滑剂的流动进行了建模和模拟[10]。李宴等应用MPS 方法计算了传动系统中单个斜齿轮的搅动损失，仿真结果与实验结果吻合较好[11]。皮彪等采用MPS 法模拟某重型减速器润滑系统，成功地将移动粒子半隐式法应用到减速器润滑分析中[12]。Deng 等在考虑轴承影响的情况下，运用MPS 方法分析研究了变速箱的润滑机理，并分析了搅油损失[3]10-12[13]。刘桓龙等运用MPS法计算得到低转速的齿轮箱飞溅润滑流场和速度场分布情况，对比了不同润滑油温度下MPS 和SPH 两种数值仿真的结果[14]。冯成程等利用移动粒子半隐式法对高速列车齿轮箱内部油流进行模拟，研究了润滑参数对齿轮箱内部流场分布的影响，并与文献对比结果一致[15]。以上研究均表明了运用MPS 法对齿轮箱内部流场进行模拟具有高可靠性和准确性。

核电循环泵齿轮箱内部行星轮系传动装置复杂，由于当前实验技术的局限性，难以准确观察到齿轮箱内部润滑油流场分布。因此，本文中采用MPS 方法建立强制喷油润滑流场仿真模型，分析内、外啮合区域附近油液粒子相关参数的变化以及油液分布对行星齿轮润滑行为的影响机制。研究内容及结论对核电齿轮箱润滑的优化设计具有重要意义。

1 移动粒子半隐式方法理论

粒子法将流体离散成一组粒子，并利用控制方程和计算算法，通过它们的速度和压力来模拟它们的运动。在本研究中，粒子的运动主要由行星齿轮的搅拌作用和粒子的相互碰撞作用引起。

1.1 控制方程

移动粒子法是一种处理不可压缩流动的分析方法，其中，连续介质是用粒子离散的。MPS方法的基础控制方程为连续性方程和Navier-Stokes方程，即

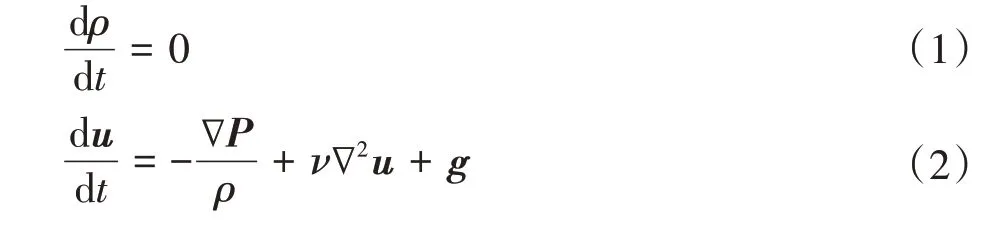
式中，ρ为密度，kg/m3；t为时间，s；u为速度，m/s；P为压力，Pa；v为运动黏度，m2/s；g为重力加速度，m/s2。

1.2 有效半径和加权函数

在MPS 方法中，粒子在核函数覆盖的相互作用区与相邻粒子相互作用。如图1 所示，有效半径re表示两个粒子间的相互作用的范围。只有当两粒子间的距离小于设定的值时，才会发生相互作用。一个粒子有效半径取为粒子直径的2～4倍。

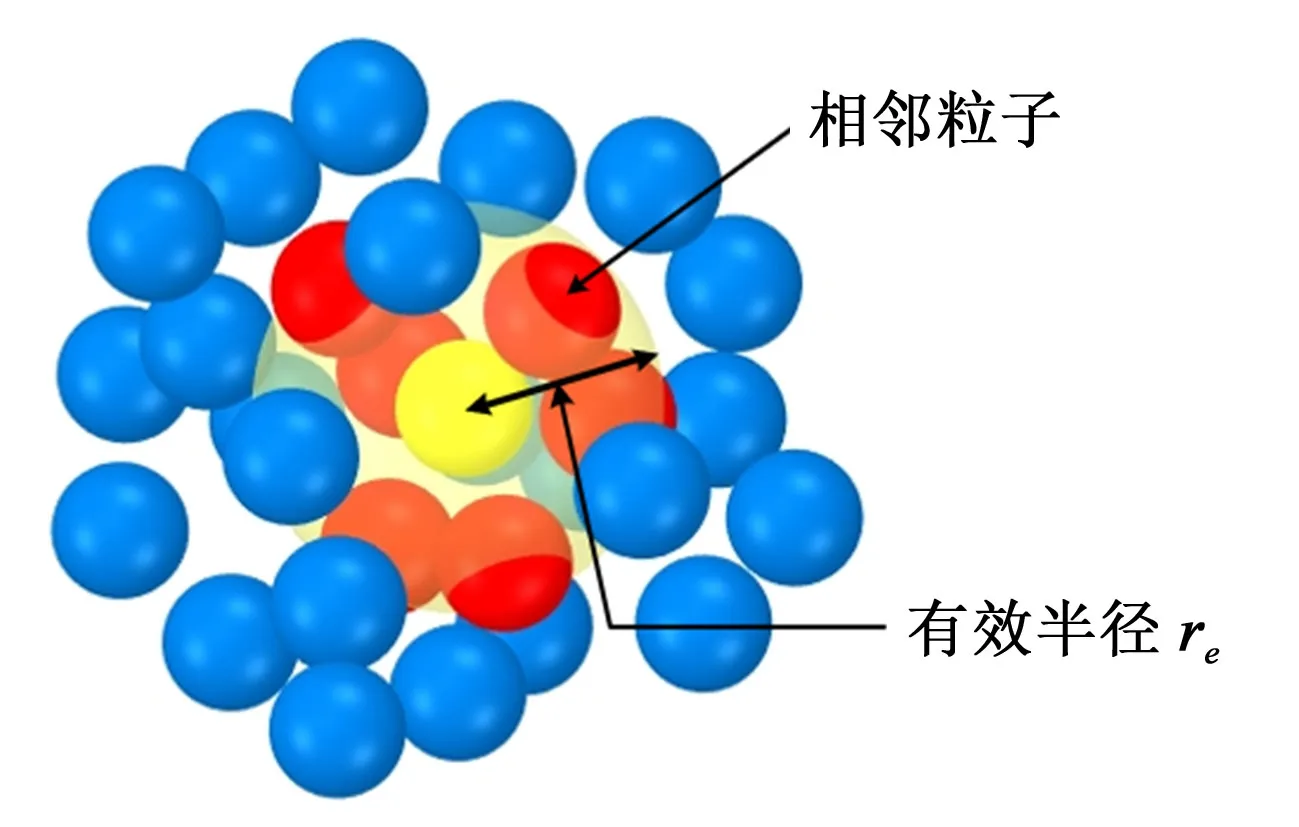
图1 有效半径的示意图Fig.1 Effective radius diagram

粒子间的相互作用是根据两粒子间的距离加权函数计算的，Weight function（加权函数）根据粒子间的距离，选定不同的方程式计算，有

式中，w（rij）为加权函数；i、j均为粒子数；re为有效半径，mm；ri为粒子i的位置向量；rij为粒子i和j之间的距离，mm。

1.3 粒子数密度与粒子碰撞

粒子i位置处的粒子数密度定义为加权函数的和。在满足不可压缩条件的粒子放置中，粒子数密度是MPS 方法所特有的参数，表示粒子放置密度的无量纲量，有

在不可压缩状态下，初始粒子数密度n0为常数，粒子排列在具有初始粒子间距离的正交晶格模式中。粒子与粒子之间碰撞产生的作用于粒子的力分为法向力Fn、剪切力Fs和阻力Fd，合力F=Fn+Fs+Fd，如图2所示。

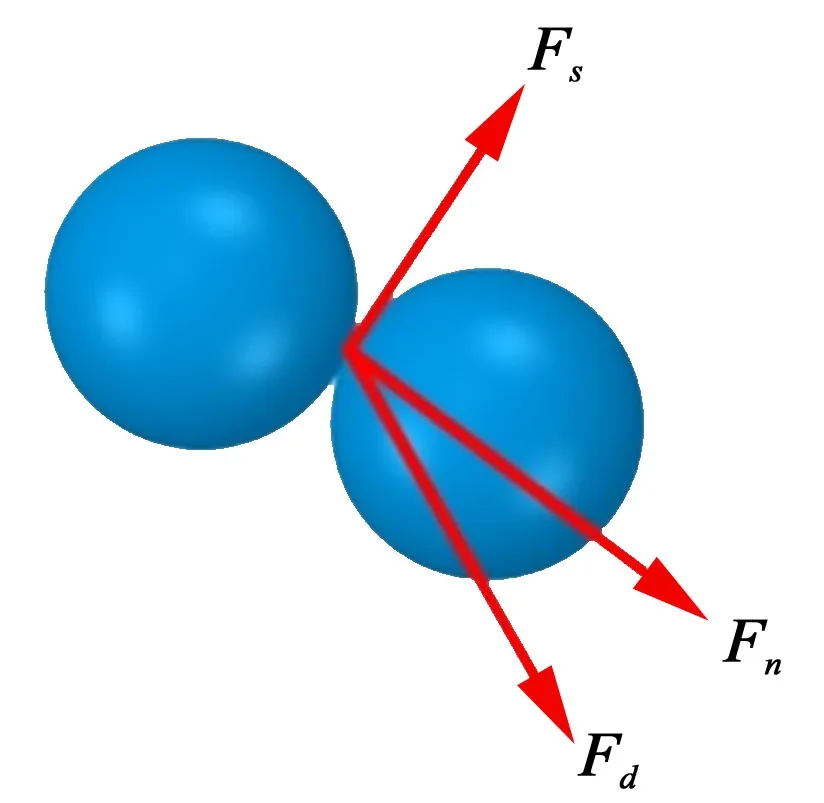
图2 两个碰撞粒子之间的力Fig.2 Force between two colliding particles

1.4 梯度模型和Laplace模型

MPS 法利用粒子相互作用的拉普拉斯变换和梯度模型来计算并校正黏度和压力，由于不需要离散Navier-Stokes 方程的对流项，可以很大程度避免数值扩散问题。其中，梯度模型是指粒子和其作用域内所有邻域粒子的梯度向量的加权平均值，示意图如图3所示，计算式为

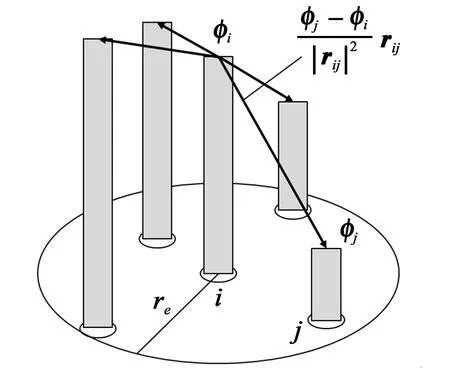
图3 MPS法梯度模型示意图Fig.3 Schematic diagram of gradient model of MPS method

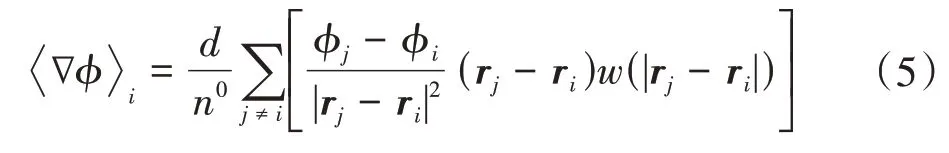
基于非正常扩散，粒子的物理量被拉普拉斯模型根据邻域粒子i的距离进行分配，即

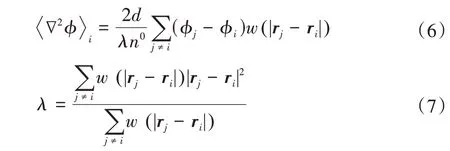
式（5）～式（7）中，ri、rj均为粒子的坐标矢量；d为求解问题的空间维数；ϕ为粒子物理参数；n0为粒子数密度初始值；λ为修正因子。

1.5 压力Poisson方程

移动粒子法是依据粒子所在的空间将微分离散化。在这里将Navier-Stokes 方程按照梯度模型和拉普拉斯算子模型处理，使用隐式方法计算压力项，其他项则被拉普拉斯模型以显式方法计算[16]。

压力项的隐式计算方程为

除压力项外，其他项的显式计算方程为

在校正步骤中，通过考虑压力梯度对速度和位置进行校正，即

式（8）～式（10）中，n为粒子数密度；n0为其初始值（n和n0是非维数参数）；上标k为指定的时间步长；上标*为显式计算中已经完成阶段的物理量。

1.6 流动阻力模型

在流动阻力模型中，流体粒子在运动中应满足修正的Navier-Stokes方程[17]，即

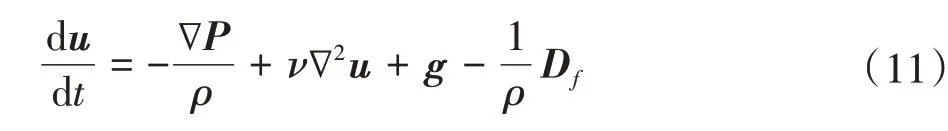
其中，流动阻力项Df的定义为

式中，Sf为一个阻力区域；a和b均为阻力系数；u′为粒子相对于阻力区域速度，速度为矢量。

本研究基于MPS 理论[7]422-424和齿轮箱内部流场和润滑模拟的具体要求，计算流程如图4 所示。首先，根据粒子初始位置、速度和压力计算粒子运动，通过压力泊松方程计算压力和修正速度；然后，输出该时间步的粒子参数，并继续下一个时间步。

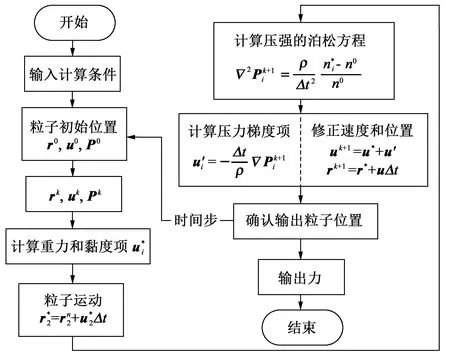
图4 粒子法计算流程图Fig.4 Calculation flow chart of particle method

2 建模与仿真

2.1 三维建模

核电齿轮箱采用立式NGW 结构，功率四分流[18-19]人字齿行星轮系一级传动，润滑油由油泵强制射入传动啮合区域。为了实现仿真要求，便于观察，对模型进行简化，移除箱体上的螺栓孔以及一些外部零部件，简化后的模型如图5所示。

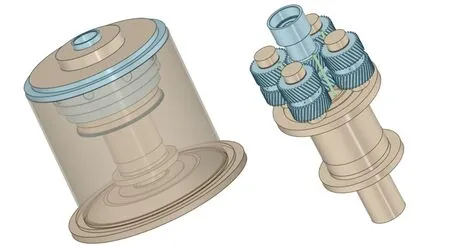
图5 简化后齿轮箱三维图Fig.5 Simplified 3D diagram of gearboxes

2.2 计算参数设置

（1）行星轮系运动参数设置。根据实际情况，太阳轮输入转速为746 r/min，行星轮自转速度为549.1 r/min，公转速度为181.3 r/min，齿圈固定不动，动力由行星架输出。

（2）润滑油参数设置。该型核电齿轮箱采用喷油润滑方式进行润滑及冷却，润滑油型号为ISO VG100润滑油，该润滑油的物性参数如表1所示。

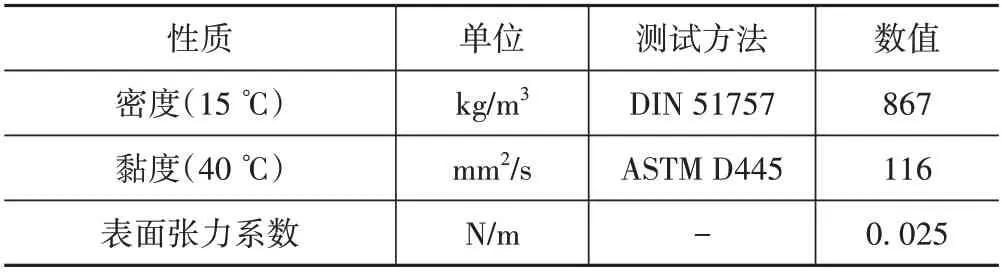
表1 润滑油参数Tab.1 Oil property parameters

（3）解析步长设置。初始时间步长太大会导致计算不收敛，初始时间步长太小会导致计算时间过长。该值由CFL（Courant-Friedrichs-Lewy）条件导出，计算公式为

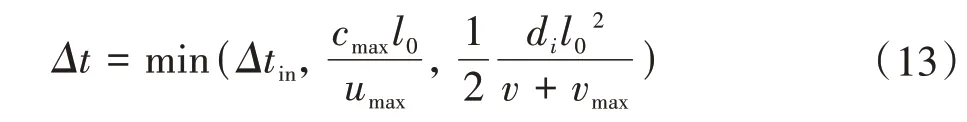
式中，Δt为时间步长；Cmax为柯朗（Courant）数，取默认值0.2；l0为粒子直径，取值0.7 mm；umax为粒子最大速度；Δtin为初始的时间步长；dil20/[2(v+vmax)]为满足黏度计算的稳定性条件。根据齿轮箱运行参数及粒子大小，取时间步长为2×106s。

2.3 仿真工况

喷油角度和供油压力是影响齿轮箱内部润滑流场的重要参数，喷油方向的改变将影响油液粒子的分布状态，供油压力的改变将影响油液粒子的喷射速度以及喷油量。其中，喷油角度θ指喷油孔和太阳轮中心点O的连线与油液粒子喷射方向之间的夹角，如图6所示。

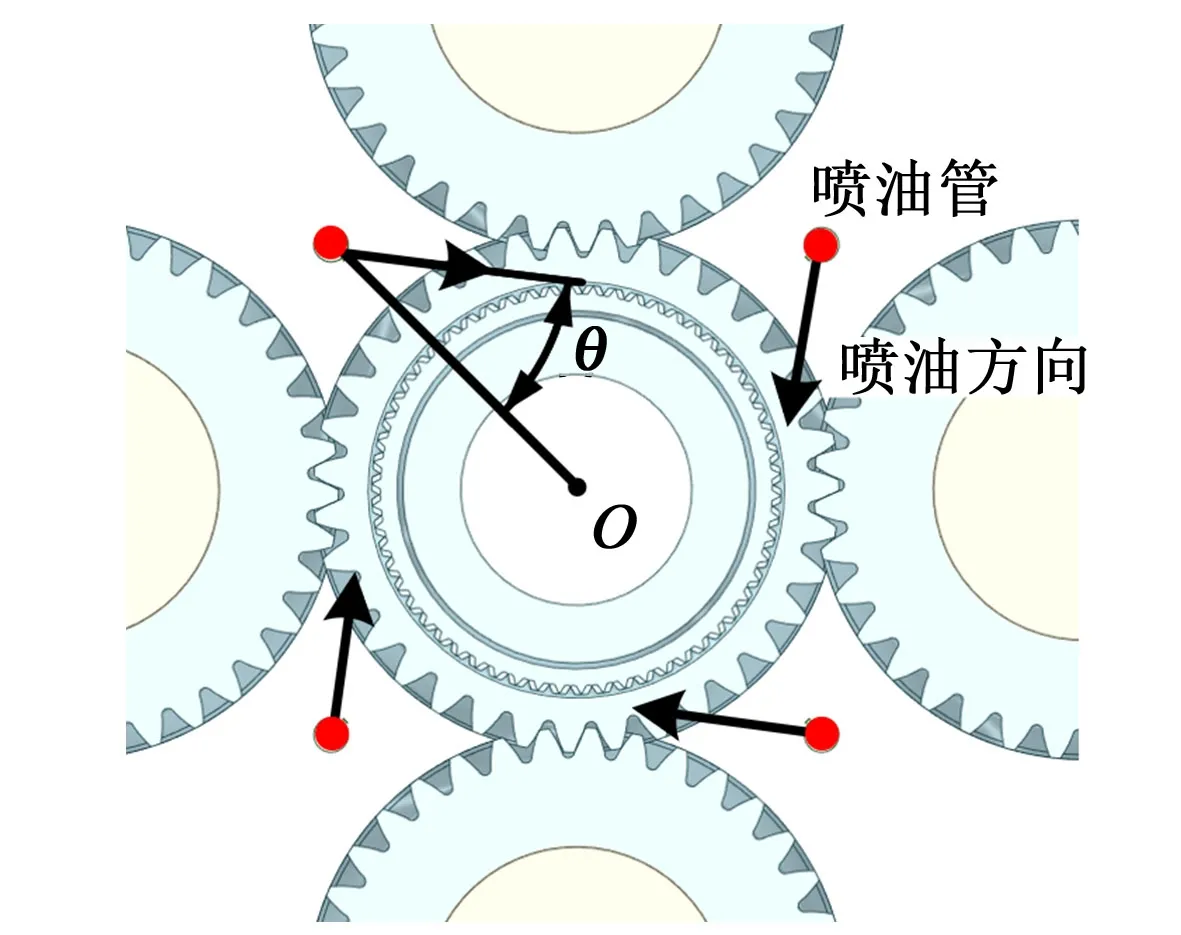
图6 喷油角度示意图Fig.6 Injection angle diagram

为研究不同喷射参数对齿轮箱润滑性能和搅油损失的影响，本文中设置5 种工况进行了仿真模拟，具体参数设置如表2所示。

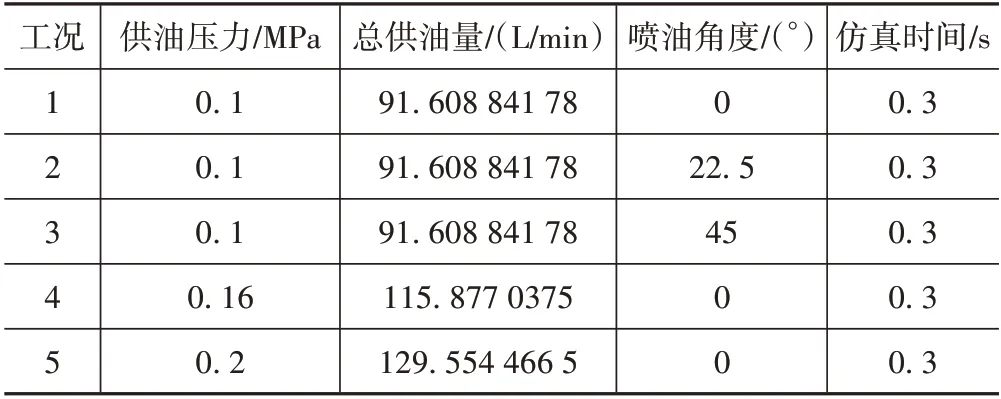
表2 仿真工况参数Tab.2 Simulation parameters

3 粒子法仿真结果分析

3.1 油液喷射角度对内部流场影响

导入模型前处理进行初始化计算，如图7 所示，对模型添加喷油润滑装置，该齿轮箱润滑方式为自带润滑油泵强制润滑。每两个行星轮之间有一个喷油管道安装在行星架上，一个管道上含6 个喷油孔，人字齿上下各3个供油孔对称分布，喷油孔实际开口直径为3 mm，共有4个管道，即共有24个喷油孔。

图7 导入的齿轮箱模型Fig.7 Imported gearbox model

图8 所示为t=0.1 s 时刻不同喷油角度下核电齿轮箱内部油液粒子分布状态。此时油液随着齿轮传动，经过太阳轮与行星轮啮合区域，随着行星轮的转动到达齿圈。高速粒子主要集中于外啮合区域。当油液到达齿圈后，由于齿圈是固定状态，部分油液将粘附于齿圈表面。低速粒子主要分布在齿圈表面以及内啮合区域。可以看出，相比于其他工况，当喷油角度为0°时，行星架与太阳轮之间的空隙更易堆积一些较低速的油液粒子。

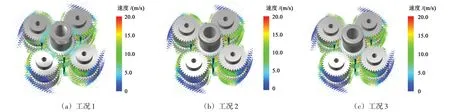
图8 t=0.1 s不同喷油角度下油液粒子速度分布状态Fig.8 Velocity distribution of oil particles in different injection angles when t=0.1 s

为了更准确地观察内外啮合区域油液粒子数目变化以及油液粒子数密度、速度大小等参数，需要采取区域探测方式。采集图9 所示行星轮内、外啮合区附近红色区域(80 mm × 220 mm × 500 mm)的粒子数量，此区域会随着齿轮的运动而转动。绘制啮合区域油液粒子平均速度、平均粒子数密度曲线图进行对比分析。

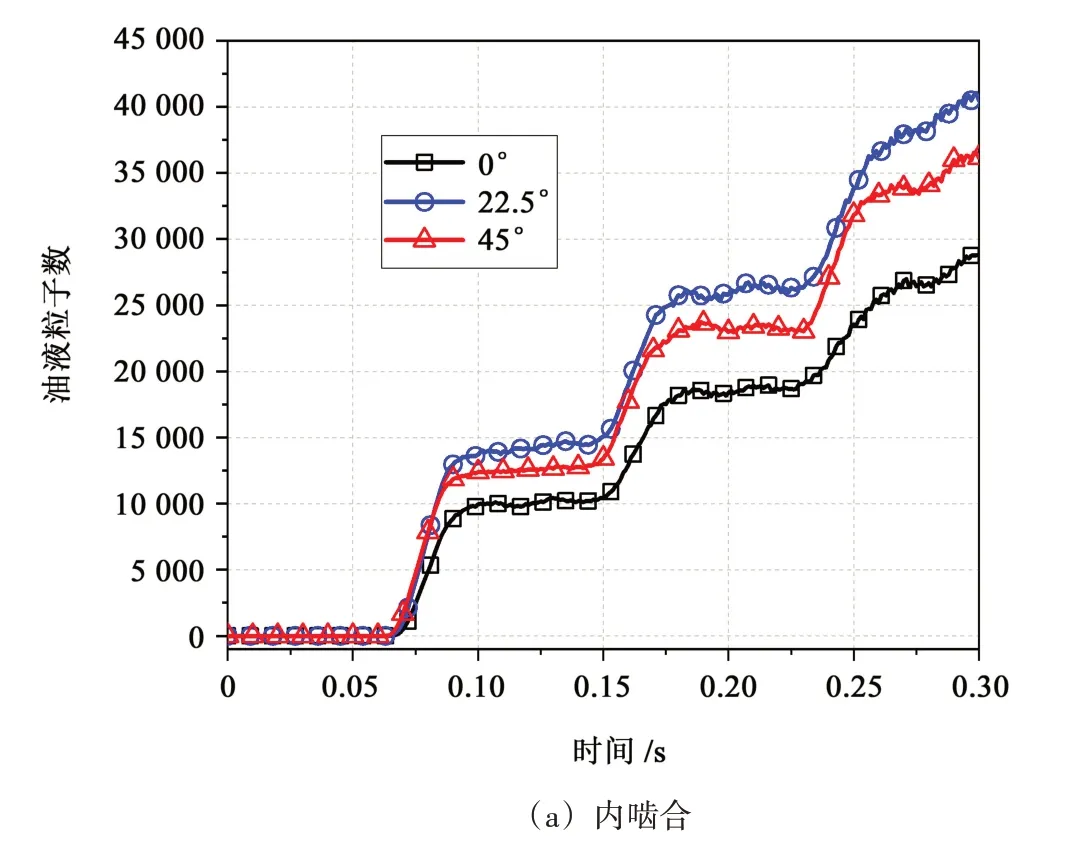
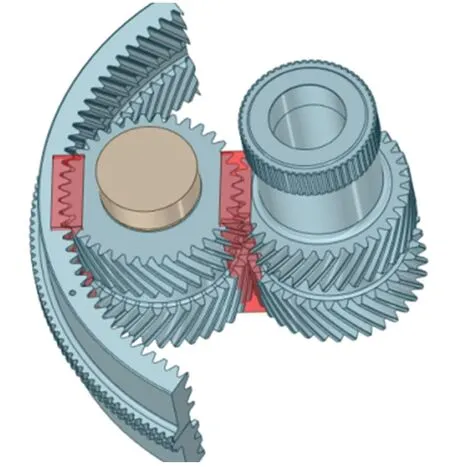
图9 粒子参数采集区域Fig.9 Sampling area for particle parameters

图10 所示为不同喷油角度时啮合区域附近油液粒子数变化情况。对于外啮合而言，喷油角度越大，油液粒子越早进入啮合区域，这是由于油液粒子的绝对速度是由喷射速度与行星轮公转速度共同决定，当喷油角度增加，相关速度矢量合成的绝对速度增大。当油液喷射角度为22.5°时，一半的油液与齿面呈现出近似垂直角度，许多油液粒子被斜齿面弹射出啮合区，而0°工况下会有更多的油液粒子粘附于太阳轮轮表面，从而被带入啮合区。当油液喷射角度为45°时，大量油液粒子粘附在行星轮上，行星轮在自转的同时，绕太阳轮进行公转，因此进入啮合区的粒子变少。对于内啮合而言，油液粒子需要更多的时间到达啮合区。内啮合区油液呈现出阶梯式增长，这是由于随着4个行星轮的公转，越来越多的油液粒子粘附在齿圈上，当行星轮经过上一个行星轮走过的区域时，该区域留有上一个行星轮在齿圈留下的油液粒子，因此，油液粒子呈阶梯式增长。

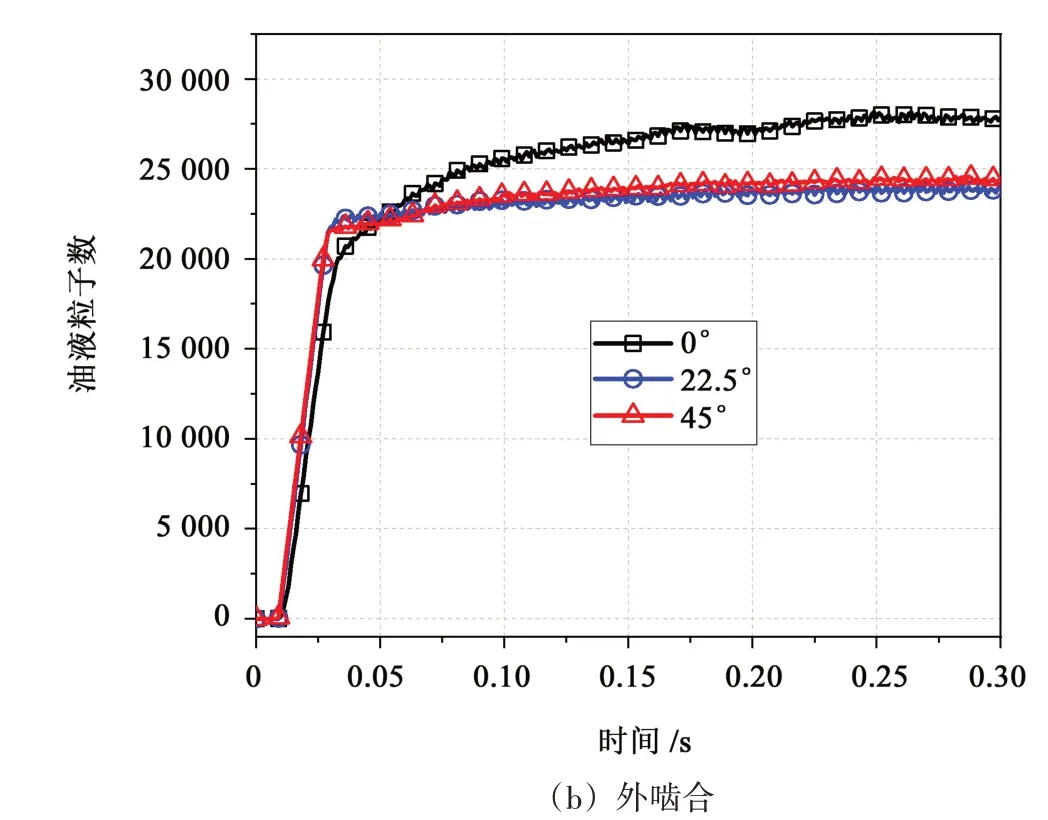
图10 内、外啮合区域附近油液粒子数目Fig.10 Number of oil particles near the inner and outer engagement region

将0.3 s 时刻一对齿轮的内、外啮合区油液粒子数转换为油液体积，截止于此时的总供油量（6 个喷油孔的总供油量），以及此刻啮合区润滑油量如表3所示。由表3 可知，喷油角度为0°时，更利于太阳轮与行星轮啮合区的前期润滑；喷油角度为22.5°时，更利于行星轮与齿圈啮合区的前期润滑；喷油角度为22.5°时，前期的内、外啮合区域油液量占比最大。

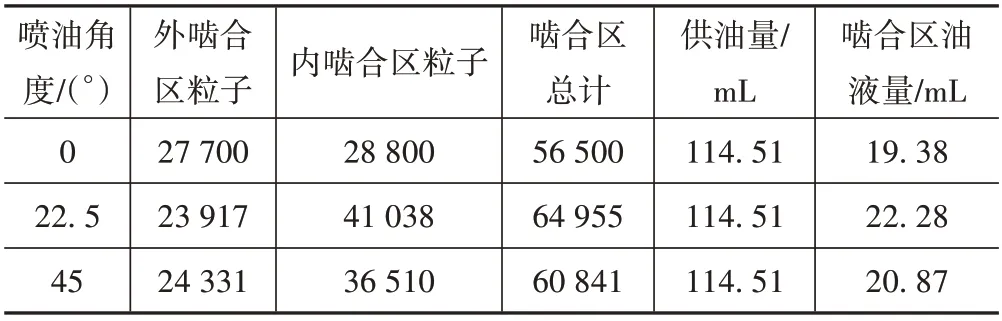
表3 t=0.3 s啮合区润滑油量Tab.3 Amount of oil in engagement zone when t=0.3 s

图11 所示为t=0.3 s 时刻工况1 核电齿轮箱内部油液粒子数密度的瞬时分布。对粒子数密度大于35 kg/m3的油液粒子进行筛选，可以看出，油液粒子团主要堆积在行星架内壁以及齿圈齿轮内表面。

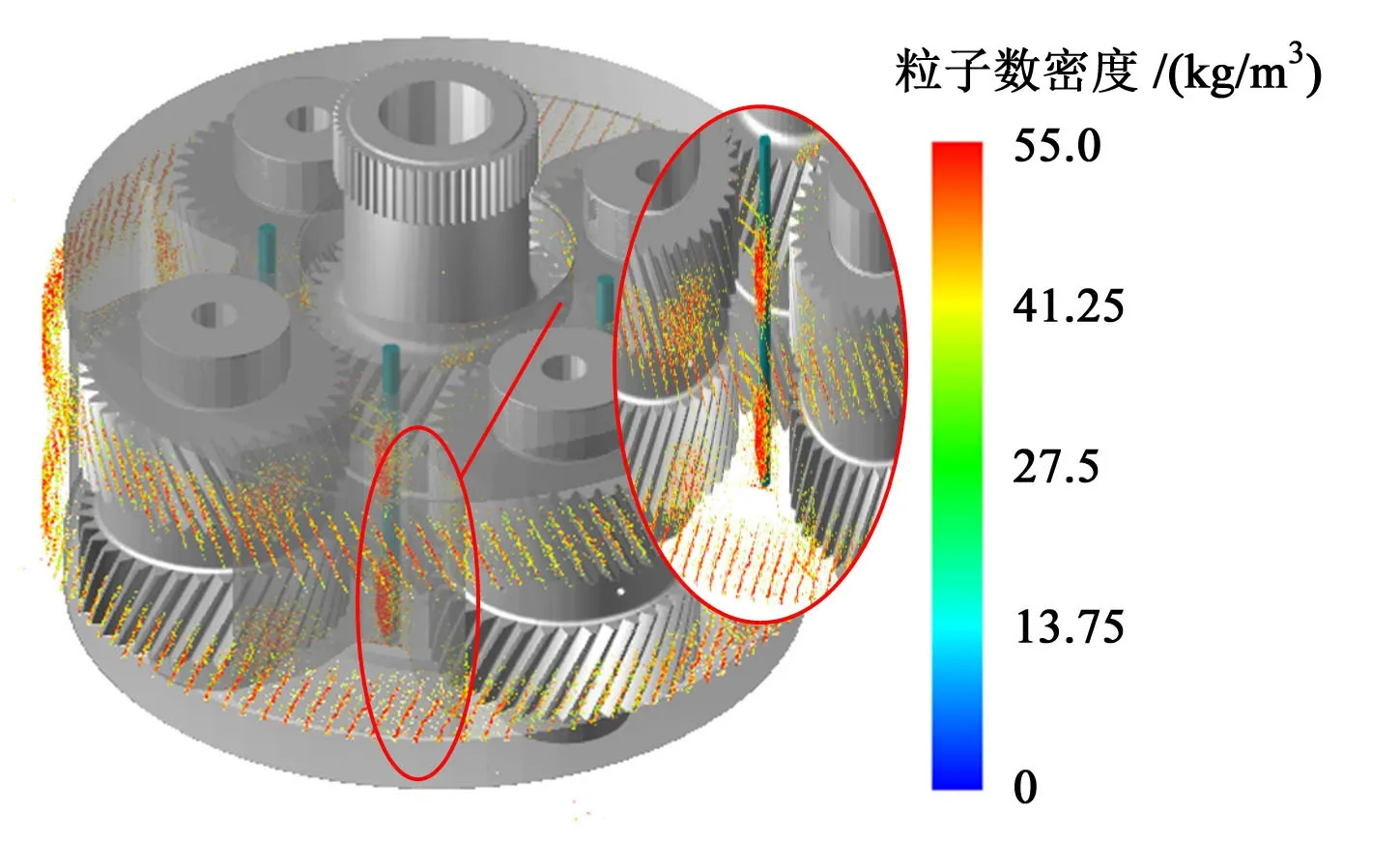
图11 t=0.3 s工况1油液粒子数密度大于35 kg/m3瞬时分布Fig.11 Particle number density greater than 35 kg/m3 in working condition 1 when t=0.3 s

图12 所示为探测不同喷油角度下，图11 所示行星轮壁面处的油液堆积量。可以看出，随着喷油角度的增加，该处的油液粒子数先减小后增大，说明适当增加喷油角度，有利于油液粘附在齿轮表面；过度增大喷油角度，会导致大量油液粒子飞溅至行星架壁面并堆积，降低润滑油的使用效率。对于具体选择某个最优喷油角度，还需进行更多工况的计算与比较。

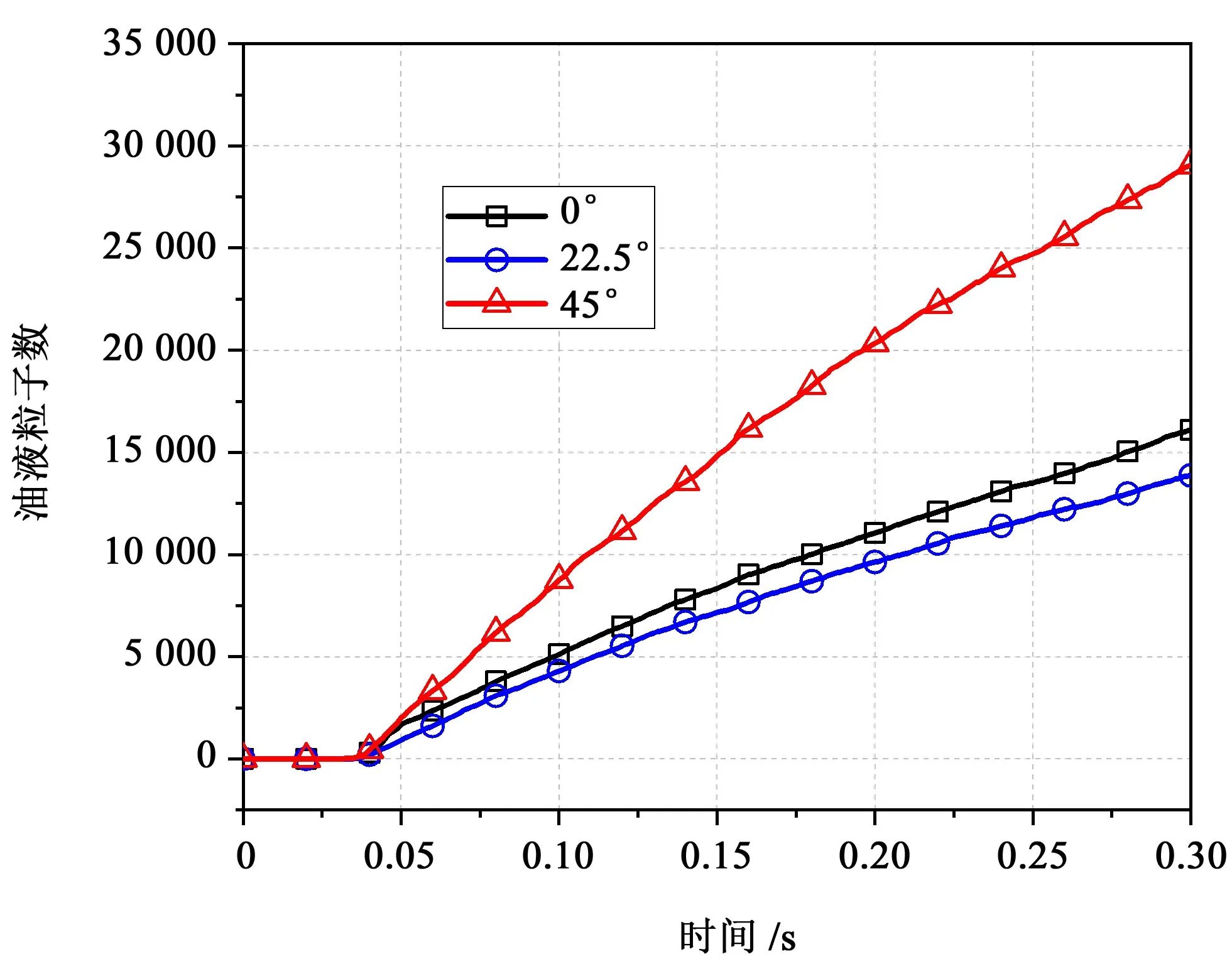
图12 行星架内壁处油液堆积量对比Fig.12 Comparison of oil accumulation on the inner wall of the carrier

图13 所示为不同喷油角度下，内、外啮合探测区域平均粒子数密度随时间变化曲线。可以看出，随着喷油角度的增加，内啮合区油液密度增大，这与齿圈上油液粒子数的增加相关，且油液直接喷向外啮合区域，以成股喷射的状态进入红色采集区域，因此，初期外啮合区域附近的油液粒子数密度骤增，稳定过后，外啮合区域油液粒子数密度先减小后增大，即适当增加喷油角度，外啮合区油液粒子变得分散，过度增加喷油角度，会使外啮合区域油液成团聚集。

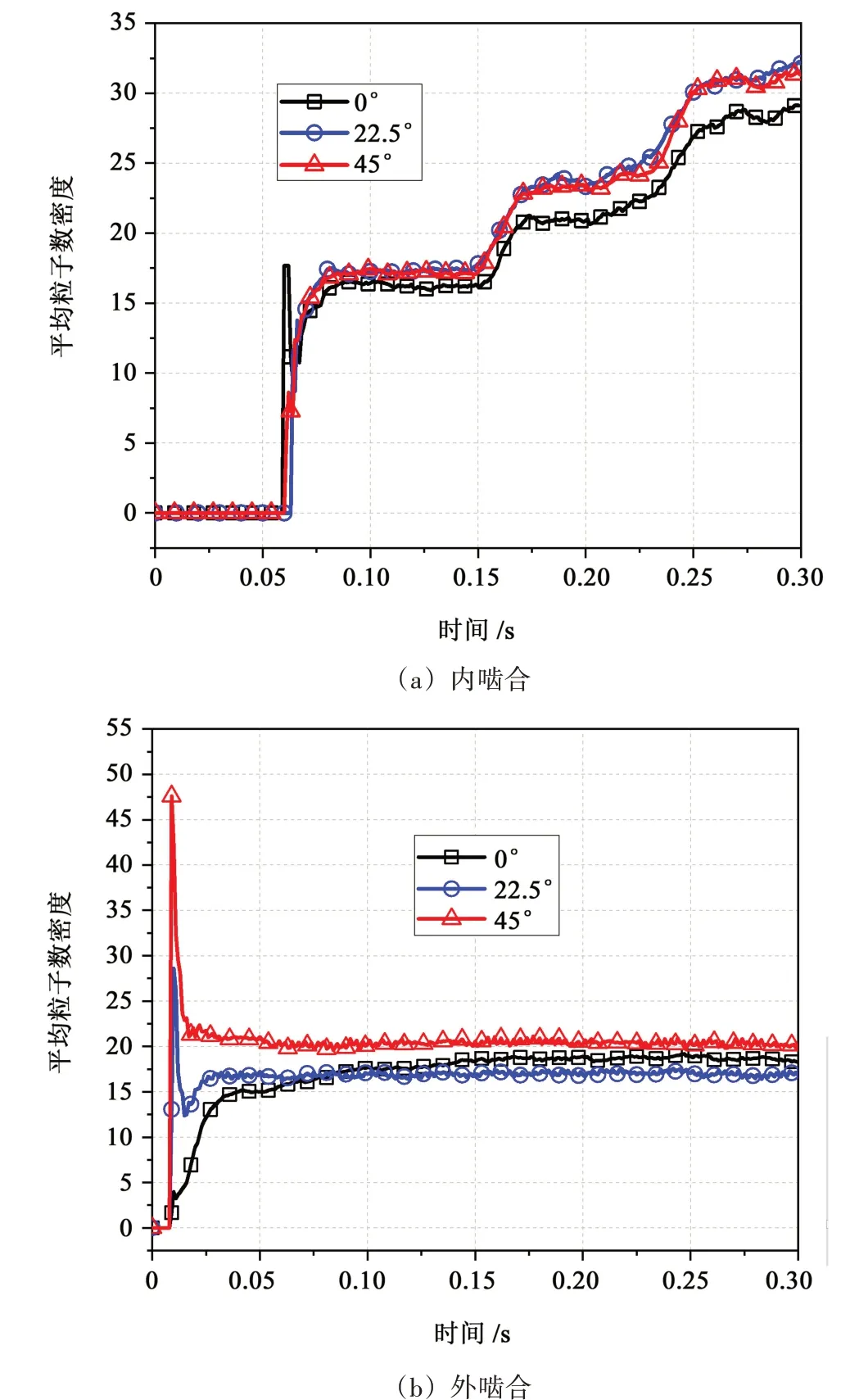
图13 内、外啮合区域附近油液平均粒子数密度Fig.13 Average particle number density of oil near the inner and outer engagement region

3.2 供油压力对内部流场影响

图14 所示为t=0.1 s 时刻不同供油压力下核电齿轮箱内部油液粒子瞬时分布状态。此时油液粒子已经到达齿圈内啮合区域，且油液经过的齿圈表面处将留有大量粒子粘附于齿圈表面，由于齿圈是固定不动状态，粘附于齿圈表面的油液粒子都为低速状态。对于行星轮而言，外啮合入口一侧的油液粒子明显少于外啮合出口一侧，这是因为行星轮的转向导致大多数粒子都进入了外啮合区域，并且从外啮合出口一侧随行星轮到达齿圈。此时随着供油压力的增加，行星齿轮箱内粒子数增多，油液分布更加饱满。

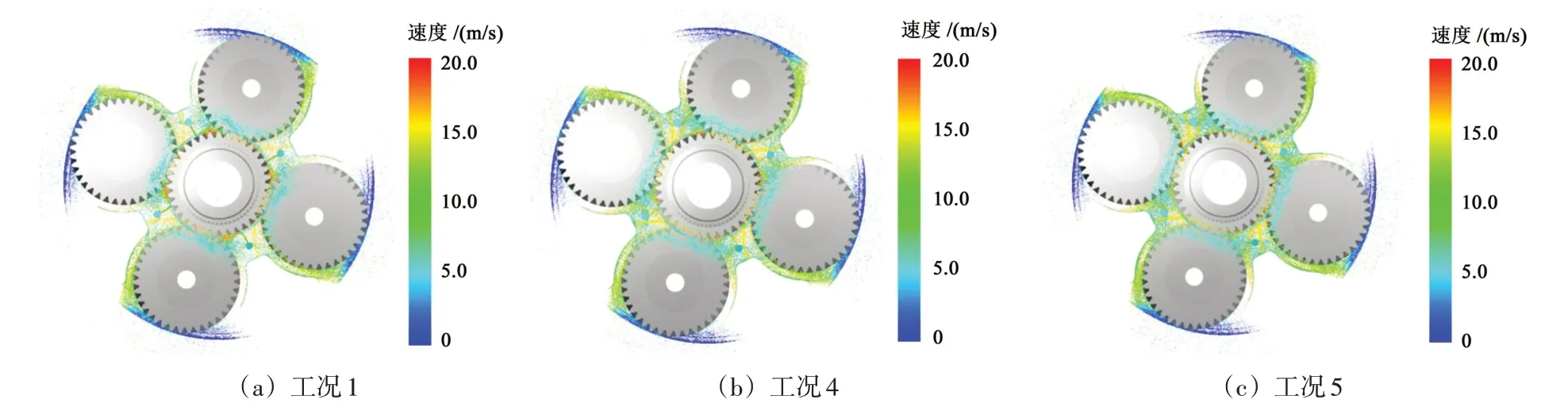
图14 t=0.1 s不同供油压力下油液粒子瞬时分布状态Fig.14 Instantaneous distribution of oil particles under different oil supply pressures when t=0.1 s

图15 所示为工况1 在t=0.3 s 时刻核电齿轮箱内部油液粒子速度分布状态。为了更准确分析供油压力对内、外啮合区域粒子数目的影响，采集图9所示行星轮内、外啮合区附近红色区域的粒子数量，分析工况1、工况4 和工况5 不同供油压力下，太阳轮与行星轮、行星轮与齿圈啮合区域附近粒子数随时间的变化如图16 所示。对于外啮合区域，比较3 种工况可以看出，随着供油压力的增加，外啮合区域油液粒子数明显增加；对于内啮合区域，油液粒子数随着供油压力的增加并无明显变化。因此，适当增加供油压力，更有利于外啮合即太阳轮与行星轮啮合区的润滑，而对于行星轮与齿圈啮合区的润滑没有太大影响。

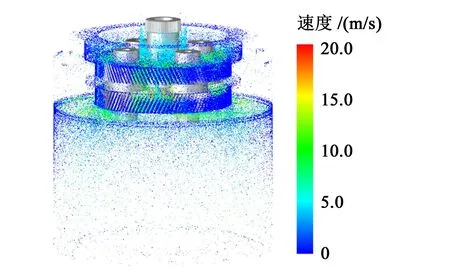
图15 t=0.3 s工况1油液粒子速度分布状态Fig.15 Velocity distribution of oil particles under working condition 1 pressures when t=0.3 s

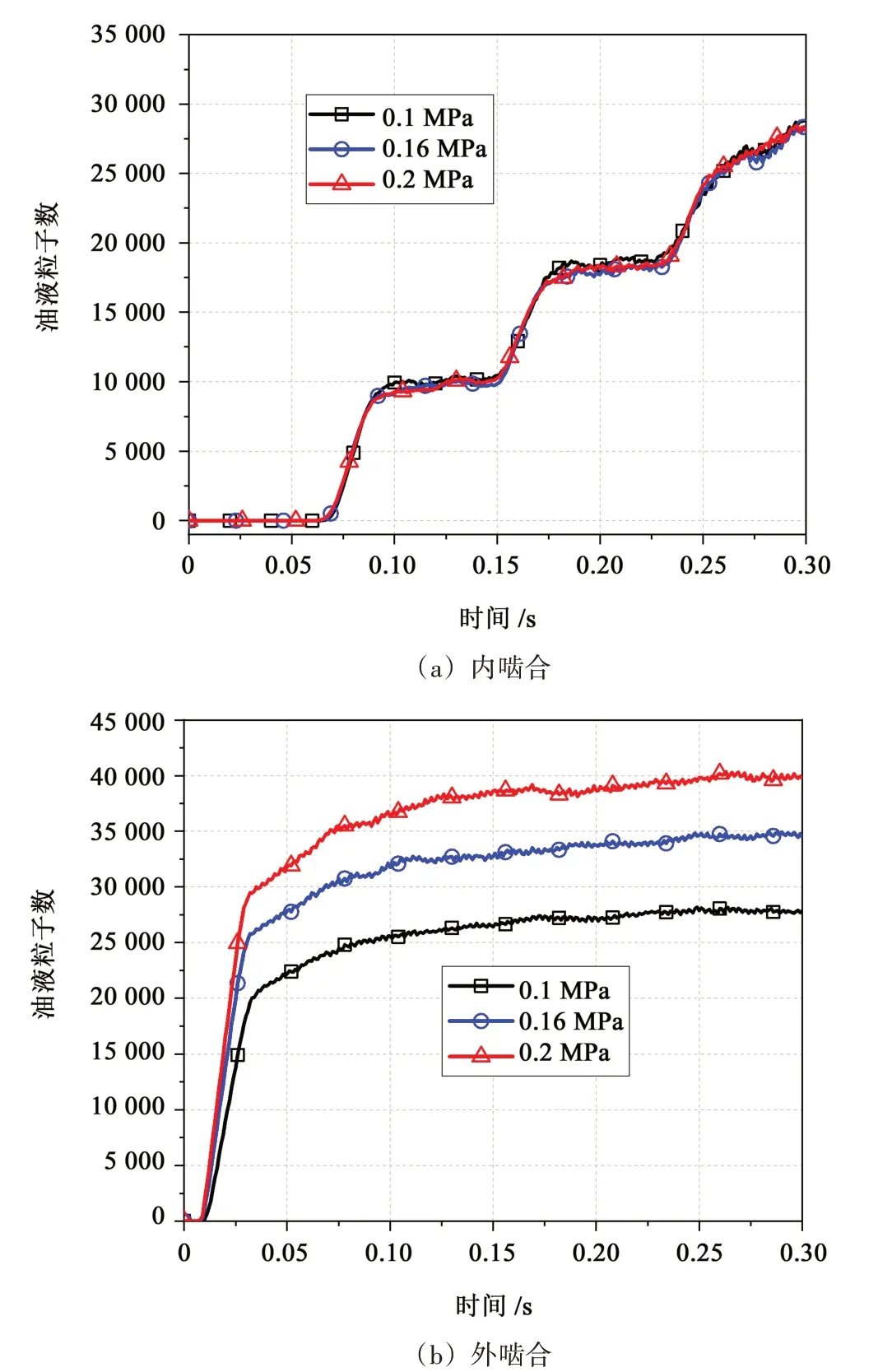
图16 内、外啮合区域附近粒子数变化Fig.16 Variation of particle number near the inner and outer engagement region

将t=0.3 s 时刻一组行星齿轮的内、外啮合区油液粒子数转换为油液体积，截止于此时的总供油量（6 个喷油孔的总供油量），以及此刻一组行星轮系内、外啮合区润滑油量具体数值如表4 所示。由表4可知，供油压力为0.2 MPa 时更利于太阳轮与行星轮啮合区的前期润滑，且供油压力对内啮合区域润滑油量影响不大；当供油压力为0.2 MPa 时，前期的内、外啮合区域油液量占比最大。

表4 t=0.3 s啮合区润滑油量Tab.4 Amount of oil in engagement region when t=0.3 s

图17 所示为不同供油压力下行星齿轮箱内速度大于15 m/s 的粒子的分布状况。可以看出，速度最大的粒子主要出现在外啮合区域附近，其余高速粒子部分成股飞溅至下一个行星轮，另一部分高速粒子将随行星轮运动到达齿圈。随着供油压力的增加，高速粒子的数目有所增加；改变供油压力，只对油液粒子进入啮合区那一刻的平均速度有所影响，待油液粒子进入啮合区后，其平均速度几乎不受供油压力的影响。即供油压力主要影响齿轮箱内的油液粒子数目，尤其是有利于外啮合区域的润滑，而对箱体内油液速度大小影响不大。

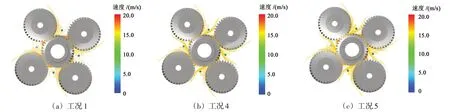
图17 不同供油压力下u＞15 m/s的粒子的分布状况Fig.17 Distribution of oil particles when u＞15 m/s under different oil supply pressures

图18（a）所示为t=0.3 s 时刻、工况5、供油压力为0.2 MPa 时核电齿轮箱内部油液粒子数密度的瞬时分布。油液粒子成团聚集的区域主要是两行星轮之间的行星架内壁连接处以及俯视状态下行星轮右侧的行星架边缘处，这是由于前文提到的油液粒子穿过外啮合区后飞溅到行星架上，导致油液聚集在此，其余高密度粒子还聚集在齿圈齿面上。采集图11所示行星轮内壁堆积的油液粒子数，绘制曲线如图19所示。对比0.1 MPa，当供油压力分别增加至1.6 倍和2倍时，该位置的油液粒子数分别增加至2倍和2.5倍，即增大供油压力会降低油液的有效使用率。

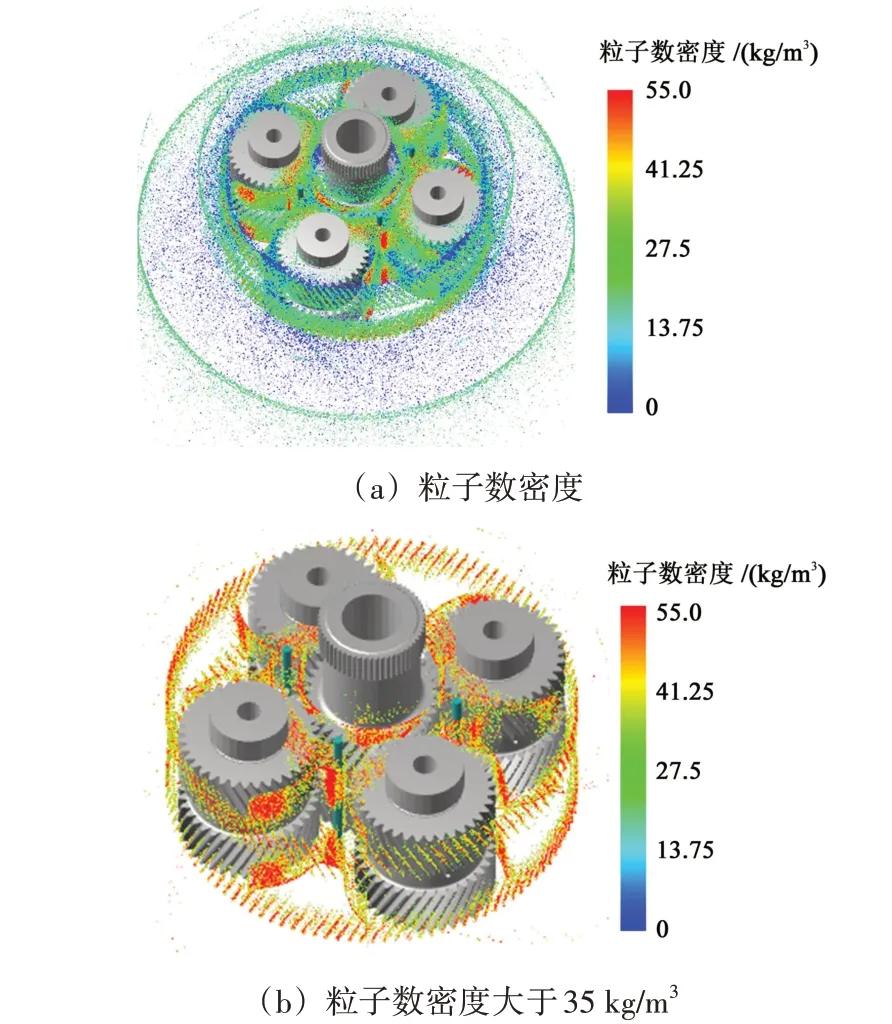
图18 t=0.3 s工况5核电齿轮箱内部油液粒子数密度分布Fig.18 Number density distribution of oil particles inner nuclear gearboxes in working condition 5 when t=0.3 s

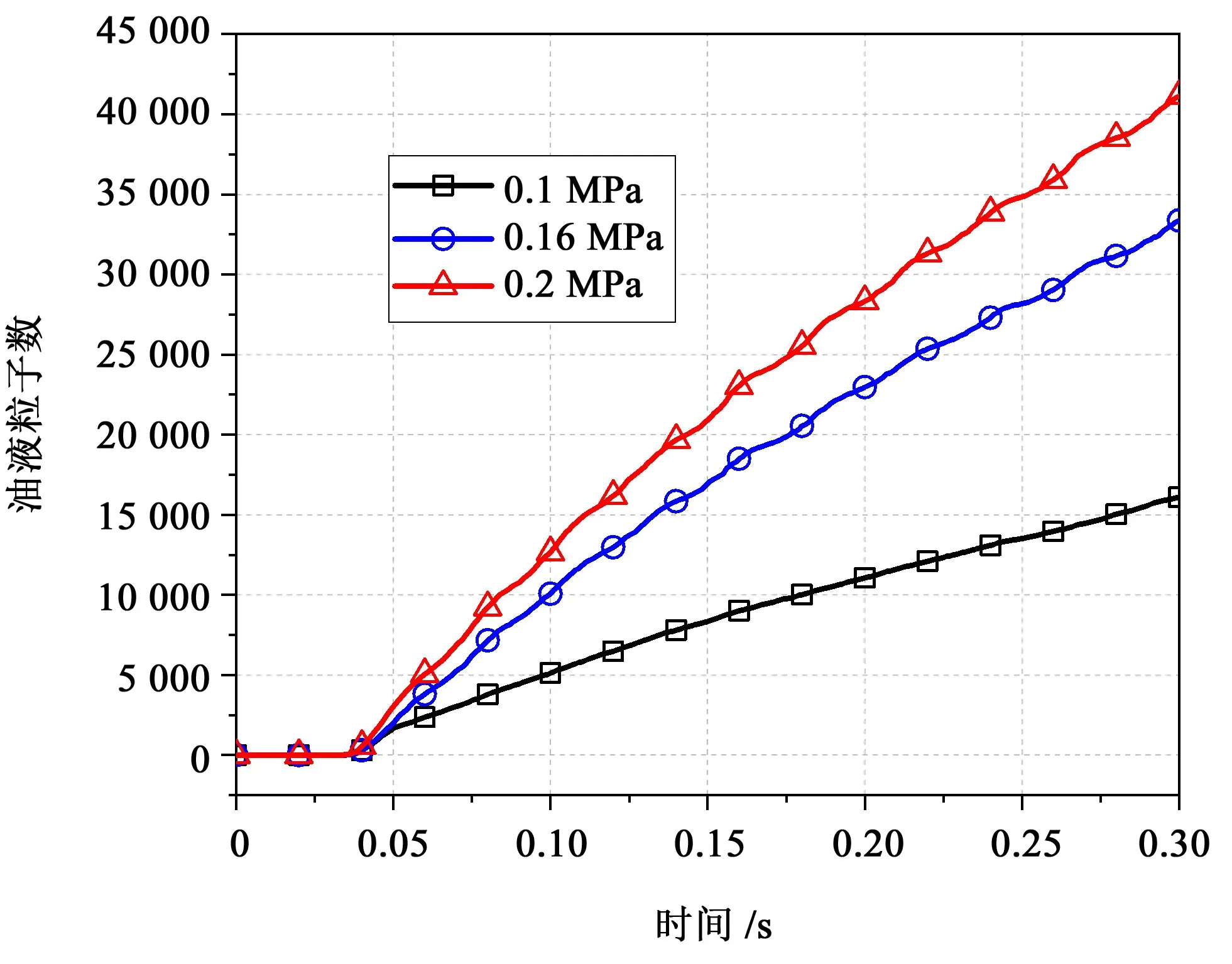
图19 不同供油压力下行星架内壁油液堆积数量对比Fig.19 Comparison of oil accumulation on the inner wall of the carrier in different oil supply pressures

4 结论

通过合理简化核电循环泵齿轮箱的三维模型，采用运动粒子半隐式方法对核电齿轮箱强制喷油润滑流场进行仿真模拟，研究了喷油角度、供油压力对核电齿轮箱喷射式润滑流场的影响，结论如下：

（1）喷油孔喷出的油液粒子随着齿轮传动，油液进入外啮合区域，再经过行星轮的转动到达齿圈，部分油液将粘附于齿圈表面。整个内外啮合区域及齿轮表面均匀地分布着油液粒子，说明行星轮系喷油润滑具有可靠性。高速粒子主要集中于外啮合区域，低速粒子主要分布在齿圈表面以及内啮合区域，行星架内表面堆积了大量油团。

（2）随着喷油角度的增大，油液喷射速度有所增加，在仿真时长内，内啮合区油液呈现出阶梯式增长，油液粒子数随着喷油角度的增加先增大后减小，喷油角度过大，将导致油液喷射到行星轮上，不利于油液进入外啮合区。当喷油角度为22.5°时，内、外啮合区总油液粒子数目最多。

（3）供油压力增大导致供油量增加，油液更早接触到太阳轮并进入啮合区，齿轮箱内油液粒子分布更加饱满，油液粒子速度分布趋势一致。随着供油压力的增加，外啮合区域油液粒子数目明显增加，内啮合区域油液粒子参数无明显变化。当供油压力为0.2 MPa 时，前期内、外啮合区域油液量最多，但也会使油液有效使用率下降。