可见光波长的测量

张 宇，陆欣雨，王凯杰，李 硕，王俊星*

(1.吉林大学 物理学院，吉林 长春 130061；2.吉林大学 仪器与电气工程学院，吉林 长春 130061)

在人类历史上，托马斯·杨利用“杨氏双缝干涉实验”第一次测出光的波长，这使光学研究进入了波动光学时期。可见，便捷准确地测量光的波长对于光学以及其他相关学科的研究具有重要意义。光的波动性主要表现为光的干涉现象和衍射现象，而利用光的干涉现象来测量光的波长是普遍使用的方法。早期世界上著名的光的干涉演示实验有：迈克耳逊干涉仪、法布里——珀罗干涉仪、牛顿环实验[1]。可见光波长测量出现误差的因素很多,如:杂散光、噪声、基线平直度等等。这导致可见光波长测量的精度过低。所以，光学仍是当下研究的热点，因此也诞生了一些测量光波长的新方法，如光栅法、密集波分复用技术、傅里叶红外光谱仪[2]。同时这些方法的测量范围也变得更大，可以用来测量激光、微波的波长。总体来看，测量光波长的仪器是向原理简单，容易实现，结构紧凑，体积小，易于便携，成本低的方面不断发展[3]。

1 设计思路

基于光的波动性，我们可以利用衍射光栅及光栅方程测量可见光波长精确值。衍射光栅基于夫琅禾费多缝衍射效应工作，原理上是由一组等间距的无限长无限窄狭缝组成，狭缝之间的间距为d为光栅常数。当波长为λ的平面波垂直入射于光栅后，在单缝衍射和多缝干涉共同作用下，可在另一侧形成各级明亮条纹。各衍射条纹的衍射角φ满足下列条件：

dsinφk=kλk=0,±1,±2

(1)

公式(1)为“光栅方程”。k为衍射光线与入射光线的夹角，称衍射角，λ为入射光波的波长，k表示级数，k=0的谱线称为中央明纹，其他级次谱线位于中央明纹的两侧，对称分布，同一级谱线按不同的波长，从短波向长波散开，形成彩色谱线。

本实验光源采用汞灯。选用波长较丰富的汞灯做光源，可观察到多级次的彩色条纹，且间距较大，有利于减小测量误差[4]。实验中有四条可见光谱线：404.656 nm(紫)、435.833 nm(蓝)、546.074 nm(绿)、579.066 nm(黄)，如图1所示。在实际测量中，由于蓝光和紫光波长较短，难以清晰观察到，因此，我们只针对绿光与黄光进行观察和测量。

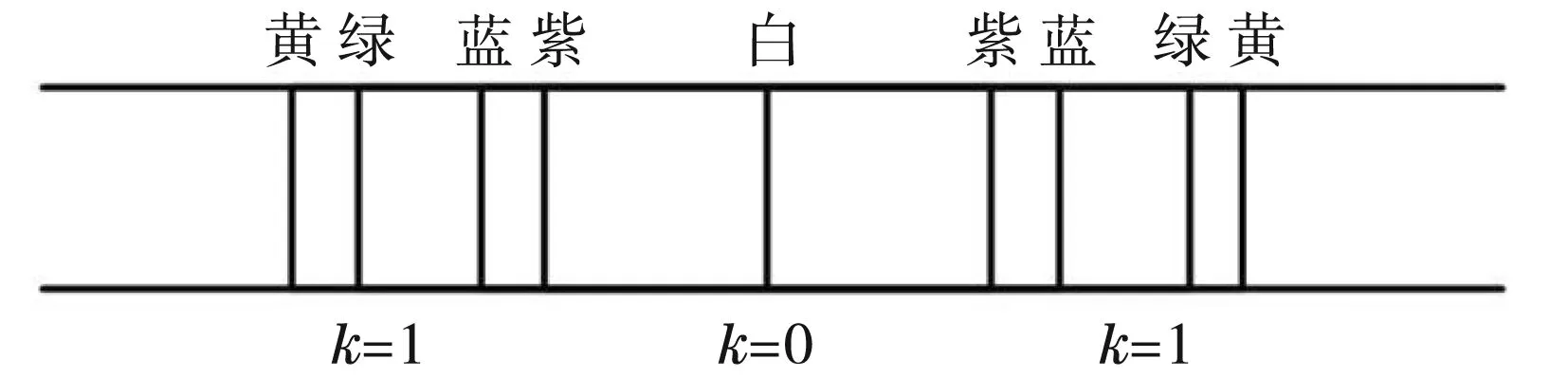
图1 汞灯衍射光谱图

当通过狭缝的光源经过已知的光栅后，在观测平面有相应干涉条纹，根据公式(1)，需获得sinφ，如图2所示，即测量AB和OA，由于φ很小，对应AB很小，难以准确测量。但观察者逆着光方向却可观察到放大的衍射条纹虚像，通过在狭缝平面添加遮光板，实验者在装置末端观察，可观察到呈现在遮光板上的虚像，根据ΔOA′B′和ΔOAB相似，测量出OA′和A′B′便可得到待测条纹的sinφ。观察k=1级条纹，在狭缝和光栅间加入长度测量仪，移动侧面鼓轮，使其指针分别对应在条纹位置处，此时ΔOA″B″和ΔOAB相似,分别获得OA″(y)和A″B″(xn),则

(2)

其中，d为光栅常数(d=1/300 mm)。为了避免在测量y时带来的误差，选一已知条纹对应的波长(黄光λ0=579.066 nm)进行标定，即测量虚象中的黄光到中间0级条纹的距离x0，从而获得y，再测待测波长条纹虚像到0级条纹的距离,此时波长公式为：

公式3即为最终所得“虚像位置——波长公式”，因此，分别测量x0和xn便可得到待测波长λn。

我们设计的装置由光源、遮光板、长度测量仪、衍射光栅、观测限位口五部分组成，光源发出的光经遮光板上狭缝后通过衍射光栅和镜筒，由人眼接收，如图2。实验者在装置末端观察，找到呈现在遮光板上的虚像，同时移动长度测量仪上指针使其与逆向光线狭缝平面上看到的待测条纹虚像对齐，分别记录0级条纹和1级条纹所成虚像位置数据。

图2 实验原理图

为了方便、准确测量，建立“虚像位置——波长公式”(公式3)，将所测得数据代入，可求得待测可见光波长。

3 实验步骤与结果

首先，依次在导轨上放置汞灯、遮光板、长度测量仪、衍射光栅、观测限位口五个光学器件。打开汞灯，预热10 min。调整光学器件，使其等高共轴。

之后，粗调(裸眼观测)，调整仪器，使入射光垂直于狭缝和光栅平面。调整光栅角度，使其平行于水平面，使眼睛透过观察口可观察到1级甚至更多级次衍射条纹，同时，确保长度测量仪上的指针能达到条纹位置，方便测量读数。细调(透过镜筒)，调整狭缝角度，使从遮光板上观察到的对称条纹与狭缝本来有一样的形状，即狭缝与入射光垂直。顺时针或逆时针旋转光栅，使遮光板上观察到两侧条纹等高，即光栅刻度与狭缝平行，使不同颜色条纹均匀分布在遮光板刻度尺两侧，确保观察到的1级及以上级次的条纹均匀分布在0级两侧。左右旋转光栅，观察遮光板上1级条纹距离0级条纹最近时，即光栅平面垂直于入射光。

为提高测量精度，可见光波长测量仪中长度测量装置采用与迈克尔逊干涉仪结构相同的测量精度为十万分之一的设计，在测量实验前，需消除大小两个鼓轮回程差,本次实验从右向左依次测量各条纹刻度，先将指针移至中央明纹右侧。旋转长度测量仪上大鼓轮，使指针向左移动一段距离，再转动小鼓轮使指针向左移动一段距离后，将小鼓轮刻线对准0刻度线，然后，转动大鼓轮使其刻线对准整刻度线。此时，小鼓轮按之前方向旋转一周，若大鼓轮移动一个小刻度，则回程差消除[5]。

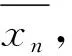
测量已知波长(黄光)和待测波长(绿光)的1级条纹的虚像位置，和中央0级条纹所在位置，作差，并取平均值得到已知波长和待测波长到中央0级条纹的距离。根据公式3计算待测波长。进行多次实验，我们测得数据如下表1所示：

表1 黄光和绿光虚像位置

对上述数据求平均值可得：

根据公式3，计算可得绿光波长的测量值为：

计算其不确定度为4nm，同时，对比了其他常见三种实验测量光波长数据，并计算其百分比误差，发现本实验的测量精度很高，百分比误差仅为0.3%。如下图3所示，与传统测量可见光的波长方法相比，百分比误差有显著下降[6-8]。

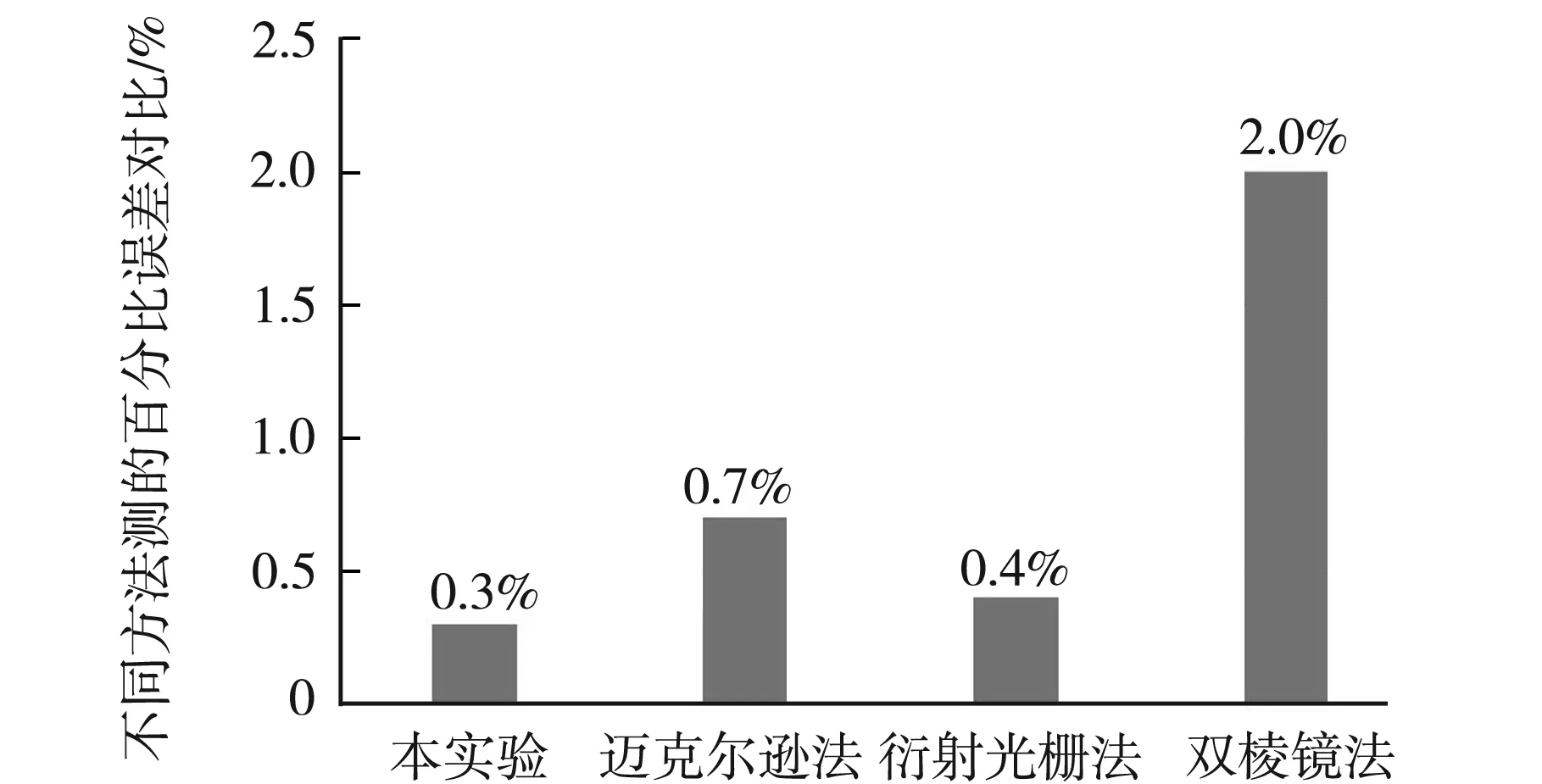
图3 不同方法测量光波长百分比误差对比

另外，根据测量结果，拟合待测波长与虚像位置的函数关系图，如下图4所示(x0和λ0为已知黄光的测量位置和波长)。

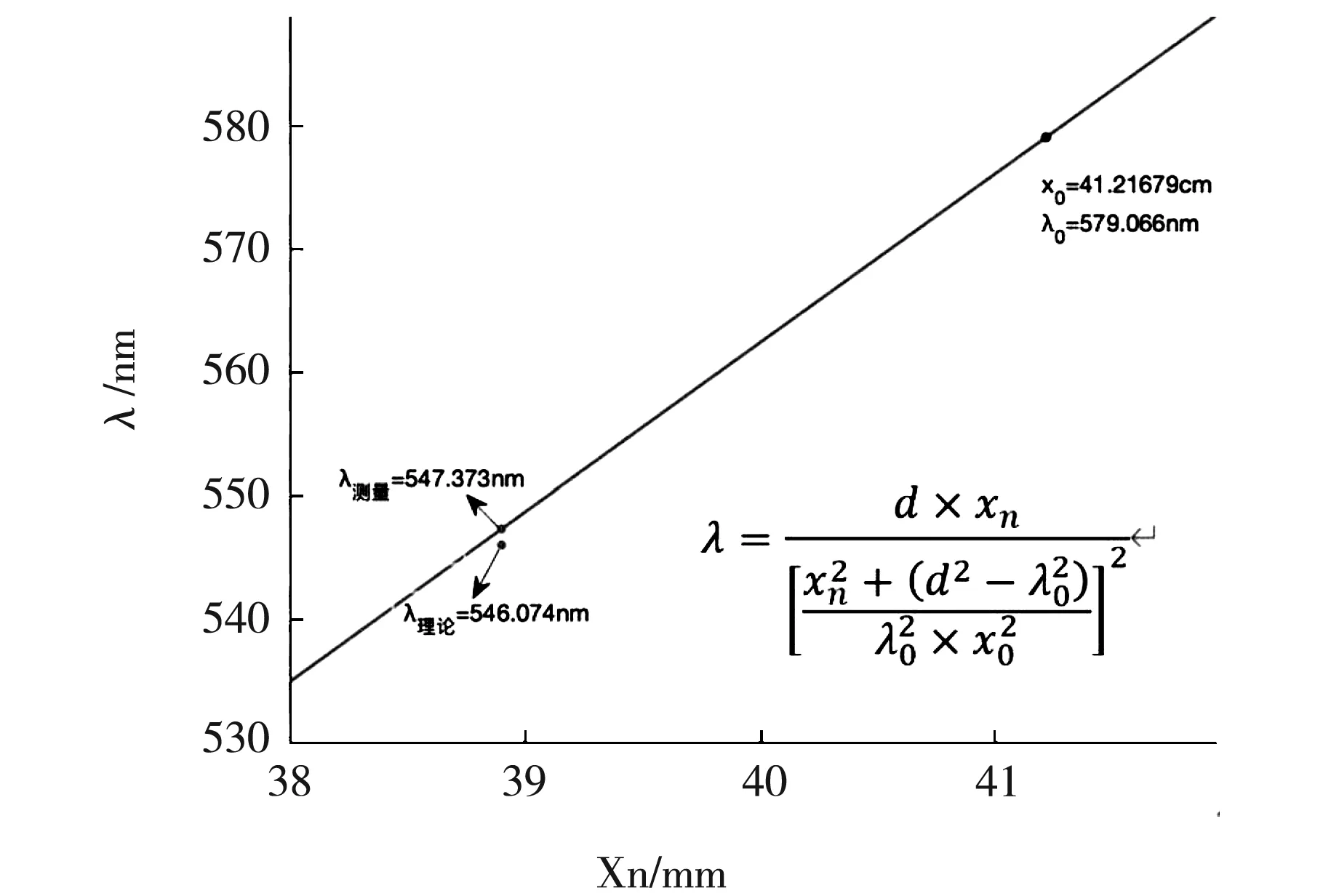
图4 待测波长与虚像位置的函数关系图

从图中可看到待测波长的测量值和理论值相差很小。通过数学推导，简化计算公式，拟合函数关系曲线，只要测出某一待测波长的1级条纹距离中央0级的位置便可在图中获得其波长。

4 结 语

本实验在理解并掌握多个大学物理实验的基础上，将传统的衍射光栅、迈克耳逊干涉仪、双棱镜干涉等仪器的优点结合，大幅提高测量结果精确度，即可读至10-8m。巧妙利用三角形相似原理，将难以测量的微小量通过几何关系进行放大，并将角度测量转换为易于操作的长度测量。实验时需要注意细节处理，如通过在遮光板粘合尺子使彩色条纹对称分布，确保了光垂直入射到光栅上；又如在观测处设置了固定位置的观察装置，减少因人眼观测位置不同而引起的误差。