聚焦波作用下平面网衣结构的水动力特性研究

俞嘉臻，张显涛，李 欣

(1.上海交通大学 海洋工程国家重点实验室，上海 200240; 2.上海交通大学三亚崖州湾深海科技研究院，海南 三亚 572000)

随着人类对海鲜需求急剧扩大，网箱养殖在近几年迅猛发展，然而由于近海的地域限制以及鱼类养殖对环境的污染，将网箱养殖转移到深远海，寻求更加优越的养殖环境，成为网箱养殖发展的必然趋势[1]。但是深远海有着更为恶劣、开放的环境，特别是可能出现的极端波浪，对网箱造成巨大的载荷，给养殖装备的结构安全带来全新的挑战。网衣作为养殖装备的关键结构之一，其水动力特性直接影响了养殖装备的动力响应。因此，研究极端波浪与网衣结构的相互作用对于养殖装备的设计与性能评估有重要的意义。

过去十年间，大多数研究聚焦于流作用下的网衣水动力特性，通过试验和数值模拟来确定流作用下网衣受力与各参数之间的关系。Fridman和Danilov[2]研究发现网衣阻力系数与雷诺数和密实度有关。Milne[3]比较了有结和无结网衣的水动力特性，发现网衣的阻力系数受结节形式的影响。Kristiansen和Faltinsen[4]提出了一种Screen载荷模型来计算定常流下网箱的水动力。Lader等[5]研究了生物附着对网衣阻力的影响，研究发现生物附着效应导致网衣阻力显著增加。Tang等[6]提出了新的网衣阻力系数计算公式，综合考虑了网衣密实度、雷诺数、网的材料以及网衣的结节形式等因素的影响。

最近，国内外的研究人员开始研究规则波下网衣结构的水动力特性，并提出了适用于网衣结构的多孔介质模型。Song等[7]研究了柔性网衣在规则波下的受力状态，发现网衣受到的水平波浪力取决于KC数和网衣参数。Lader等[8]研究了规则波和网衣的相互作用，发现网衣的水平波浪力大约是垂向力的10倍。Patursson等[9]和Zhao等[10-11]应用多孔介质模型分别模拟了在定常流作用下不同来流攻角、多网衣结构以及网箱布置下的流场变化。Bi等[12]和Zhao等[13]进一步将多孔介质模型用于模拟波浪与网衣结构的相互作用。Chen和Christensen[14]基于已有的多孔介质模型，通过与Morison模型计算的网衣受力等效分析，获得多孔介质阻力系数的直接估计方法，通过将数值模拟结果与试验结果对比，证明该模型具有一定准确性。Dong等[15]对规则波中不同类型的网衣进行了一系列试验，并提出了一种基于Morison公式的经验模型用来计算规则波下的网衣受力。

上述研究集中在研究定常流以及规则波下网衣结构的水动力特性，并建立了多孔介质模型和经验模型来求得网衣的受力。然而对于极端波浪作用下网衣结构水动力特性的研究目前还十分有限。基于waves2Foam建立数值波浪水池，极端波浪采用基于NewWave理论的聚焦波模拟，网衣结构采用多孔介质模型模拟，通过与Morison模型计算的网衣受力等效分析，获得多孔介质模拟网衣结构的阻力系数的直接估计方法。开展聚焦波与网衣结构相互作用的数值模拟，与网衣水槽试验结果作对比，验证此数值模拟的准确性。在此基础上，考虑不同的波浪参数和网衣密实度，系统研究聚焦波作用下网衣结构的水动力特性。

1 数学模型

1.1 聚焦波理论

Tromans等[16]提出了NewWave理论，用来模拟给定波峰值的聚焦波，该方法通过预定的波峰高度，分配每个频率的波浪谱能量，最后通过式(1)求得各组成波的波幅。

(1)

式中：ai为聚焦波各组分波浪波幅，Ac为聚焦波最大波幅，S(fi)为组成波对应的波浪谱(本文采用Jonswap波浪谱)，δf为能量谱的频率间隔，N为组成波数目。则基于NewWave理论的聚焦波时历计算公式为：

(2)

式中：η为波面升高，ki、ωi分别为第i个组成波的波数和圆频率，Xt、Tt分别为聚焦波的聚焦位置和聚焦时刻。如图1所示，聚焦波是一种瞬时极端波浪，属于非平稳过程，现采用局部波浪参数对其进行描述，Ac为静水面到最大波峰的垂向距离；聚焦波谱峰周期Tp为波浪组分中能量最大的波浪对应的周期；谱峰波长λp通过谱峰周期计算得到；波陡s定义为聚焦波波峰Ac与谱峰波长λp的比值。

图1 聚焦波参数定义

1.2 多孔介质模型

1.2.1 控制方程

针对多孔介质模型，Jensen等[17]得到了体积平均、雷诺平均的流体运动控制方程：

(3)

(4)

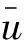
(5)

式中：C是非线性多孔介质阻力系数矩阵。

网衣受到的瞬时力是数值模拟中最重要的输出部分，式(5)描述的是多孔介质对流体的作用力，而流体对多孔介质的作用力为多孔介质所受阻力即所需要输出的部分，两者互为反作用力。多孔介质所受瞬时力Qi最终表达式为：

(6)

式中：PV是多孔介质控制区域。

另外，Van Gent[18]将多孔介质的惯性力系数Cm定义为：

(7)

式中：γp是无量纲经验系数，一般取值为0.34。

1.2.2 多孔介质阻力系数直接估计方法

获得网衣水动力系数是网衣水动力研究中关键的问题之一。一般而言，将网衣水动力系数分为阻力系数(顺流方向)和升力系数(垂直于来流方向)，也可以分为法向力(垂直于网衣平面)和切向力(位于网衣平面内)。当来流方向垂直于网衣平面时，网衣阻力与其法向力保持一致。文中主要关心网衣的阻力系数。由于数值模拟中采用多孔介质模拟网衣结构，因此，多孔介质的阻力即为所关心的网衣结构的阻力。

图2为网衣结构示意，网衣由若干网目组成，网目根据形状可划分为菱形、矩形和六边形结构，根据结节可以分为有结节和无结节两种情况。每个网目由目脚和结节构成，对于菱形和矩形网目，一般认为单个网目由4根目脚和4个结节组成。文中用到的网衣均为无结节矩形网衣。在网衣水动力计算中涉及到一个重要的参数即密实度Sn，代表的意义为网线投影面积与网衣整体投影面积的比值。

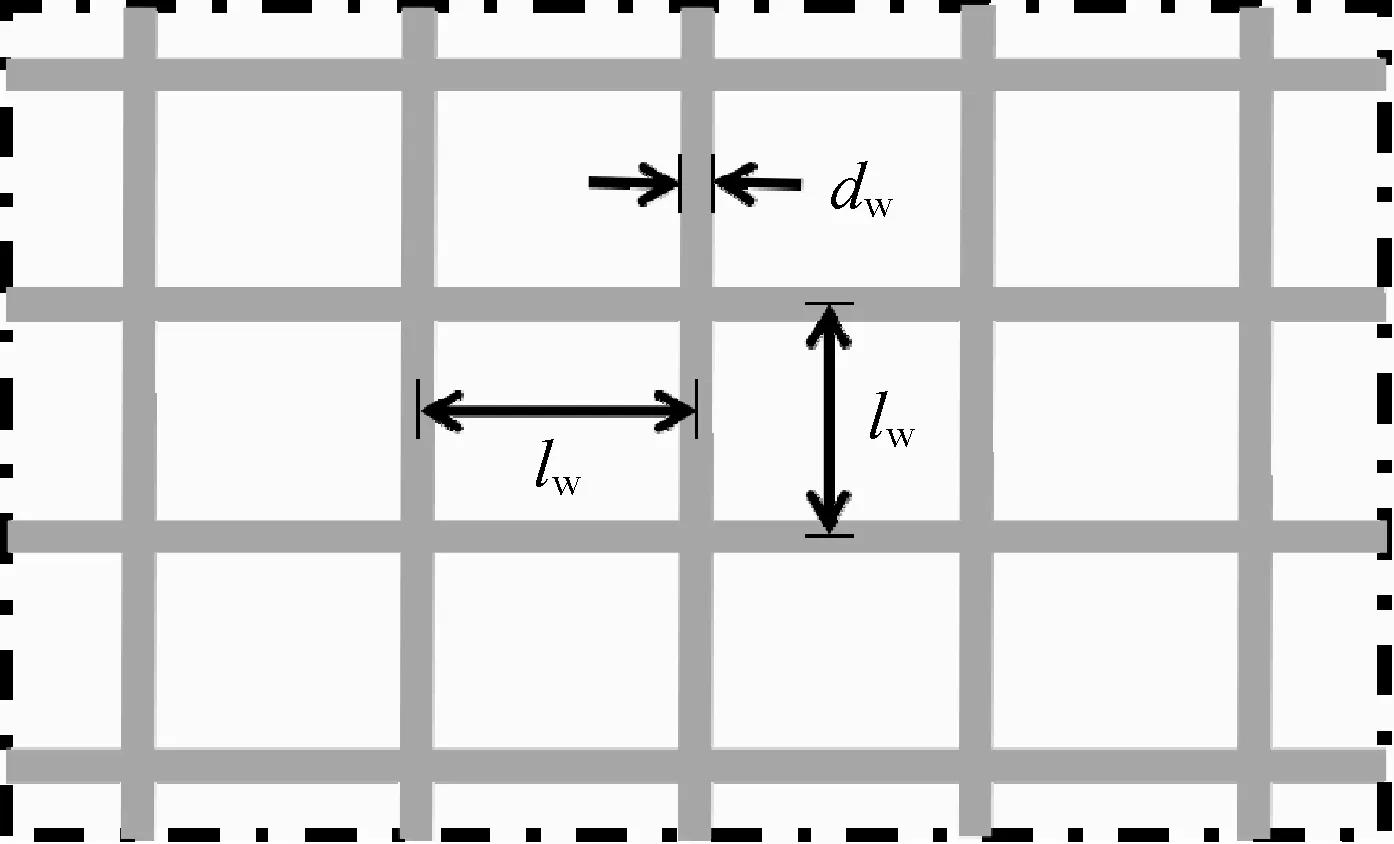
图2 网衣结构

(8)

式中：dw为网线直径，lw为网衣目脚长度。

通过与Morison载荷模型等效来得到多孔介质非线性阻力系数(即式(5)中的Cij)。假设网衣处于定常流中，且为无结节方形网衣。以网衣平面法线方向为x方向建立坐标系，网衣固定在y-z平面内，因此无需对系数进行坐标变换。水流可分解为x-y平面和z轴的分量，图3即为速度矢量的分解，θ、β表示来流速度与网衣平面之间的夹角，网衣的倾斜角通过这两个参数体现。

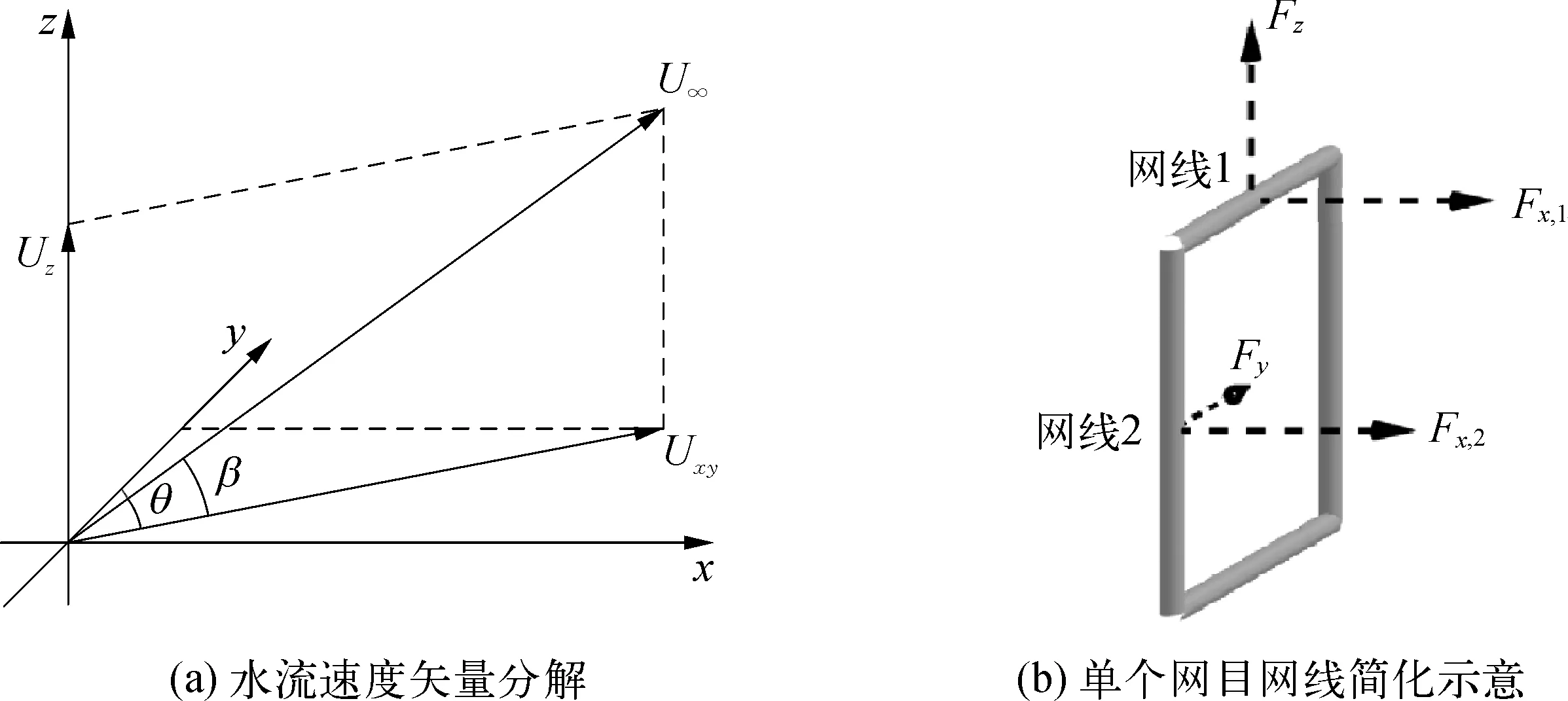
图3 水流速度矢量分解和单个网目网线简化示意

Tauti[19]在分析网衣水动力时提出了假设：网衣在水中运动时，作用在每个网目的目脚和结节上的水动力彼此独立，互不相关，因此认为作用在网衣上的总力是每个网线所受力的叠加, 单个网目有水平、竖直两类网线(如网线1和网线2),网目在x方向的受力Fx(即沿网衣平面法线方向上的受力)是网线1和网线2在x方向受力的叠加，即Fx=Fx,1+Fx,2。

(9)

(10)

(11)

式中：Fx,Fy,Fz分别为网衣在x,y,z方向上的受力，M是平行于网线2的网线总数，N是平行于网线1的网线总数，A1,A2是网线1和网线2的投影面积，Cd,twine是网线的阻力系数。基于式(6)作用在多孔介质上的力可表示为：

(12)

(13)

(14)

式中：Qx,Qy,Qz分别为网衣在x,y,z方向上所受流体的瞬时力(在下文中，Qx即为网衣阻力Fd，Qz即为网衣升力Fl)，V为多孔介质区域体积，U∞为无穷远处来流速度。由于将网衣看作多孔介质，所以作用在多孔介质上的力等于每个网线受力的总和，即F=Q，计算得到C1,C2,C3：

(15)

(16)

(17)

此外，通过正确地降低Morison模型中系数的夹角依赖性，仍然可以得到合理的结果。因此文中引入a、b两个系数来描述网线与网线之间的相互作用效应，并将角度从公式中去掉，以减少多孔介质的角度依赖性，其中的影响已经包含在a、b两个系数中。阻力系数最终表达式为：

(18)

(19)

(20)

式中：S1,S2分别为网衣内竖直网线和水平网线的投影面积。从Rudi等[20]针对不同网衣冲角、密实度的系列试验中选取试验数据对系数a、b进行拟合，通过线性插值的方法得到一定密实度下的a、b表达式：

(21)

(22)

式中：Sn为网衣密实度。

2 试验和数值模型

2.1 物理试验模型

试验在波浪水槽中进行，如图4(a)所示，该波浪水槽总长18 m，其中过渡区3 m，工作区12 m，消波区3 m；水槽宽1 m，水深可调节，试验中水深为0.86 m。造波机摇板精度误差在0.01°以下，摇摆最大幅值可达±25°，最小造波周期可达0.3 s，波高最大可达20 cm，完全满足试验的精度要求。

图4 物理试验模型

图4(b)为网衣试验装置，由网衣、夹具、细铁杆、顶部和底部固定装置及三分力传感器组成。传感器固定于夹具上，上下夹具分别和顶部铝型材、底部压铁固定连接，细铁杆固定于两个夹具上，网衣通过上下两根细铁杆与夹具连接并展开，通过调节顶部铝型材上直角钢的高度来控制网衣竖直方向上的张紧程度。其中三分力传感器量程为50 N，精度0.01 N，满足试验的精度要求。

试验利用电阻式浪高仪测量波浪升高，利用三分力传感器来测量网衣在波浪作用下受到的阻力和升力。试验中共用到两个三分力传感器，量程50 N，精度0.05%，安装在网衣装置的顶部和底部。当网衣受到波浪力时，传感器在z方向和x方向受力，数据采集系统采集传感器数据得到实时的网衣受力。此处说明在试验安装过程中，网衣的阻力方向为传感器的z方向，网衣的升力方向为传感器的x方向。在试验前需对传感器进行标定，分别得到三分力传感器在3个方向上的标定系数。

2.2 试验工况

模型试验测试了网衣在不同聚焦波作用下的水动力结果。具体的网衣参数及波浪工况如表1和表2所示。

表1 网衣参数

表2 波浪工况

在试验开始之前，首先进行了空白对照试验，即把网衣拆除。由于整个装置只有底部传感器单元浸没于水中，所以对底部的三分力传感器的受力进行监测。对在若干个波浪下的数据进行采集，发现三分力传感器在无网衣的情况下基本不受力，其幅值与无外力作用时的幅值接近，所以认为除网衣结构之外的部件对传感器的受力影响可以忽略不计。

每个工况重复3次以排除试验的偶然性并验证试验结果的可靠性。如图5所示，对比了Exp_Wave2工况下3次试验的结果。从图5中可以看出，3次试验的结果吻合度非常好，说明在波浪作用下该试验装置测得的数据重复性好，可靠性高。在下文与数值模拟结果对比时，将3次重复试验结果的峰值做对比，取中间值的那次试验作为对比数据。

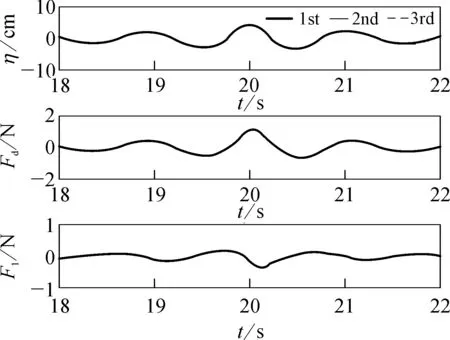
图5 Exp_Wave2工况重复性试验结果对比

2.3 数值模型及准确性验证

在数值模拟计算中，基于式(3)～(22)开发适用于计算网衣结构水动力的多孔介质模型求解器，在原有的造波工具waves2Foam中嵌入多孔介质区域。相关的参数输入包括聚焦波的波浪参数：各波浪组分的频率、波幅、波数、相位等；以及网衣的物理参数Sn、Cm、V、Cd,twine，系数a，b以及网衣中水平、竖直网线的总投影面积S1、S2。在数值计算过程中，多孔介质区域外的有限体积单元采用waves2Foam默认求解器求解波浪运动。多孔介质区域内的有限体积单元带有porosity标识，当读取到该单元时会切换到多孔介质求解器进行求解，并将每个时间步长的计算结果进行保存。为得到想要的网衣受力结果，对多孔介质区域内的有限体积单元计算得到的阻力和升力进行积分并实时输出到结果文档，得到实时的网衣受力结果，具体计算过程如图6所示，多孔介质区域内的有限体积元e1，e2……en，每个有限体积元处的速度场都已知，根据式(6)得到每个有限体积元的瞬时力，最终将多孔介质区域的所有有限体积元进行积分得到整个多孔介质区域即网衣的瞬时力。为得到波浪在网衣结构下的演化特征，在数值水槽若干处设置“浪高仪”，浪高的计算原理是基于局部水体积分数α(在流体中α=1，在空气中α=0)积分求得该监测点的水深。下文中的结果都基于上述的输出文档数据进行分析。

图6 数值模拟结果输出

所建数值波浪水池参照实际水槽尺寸设计，基于waves2Foam来开展聚焦波与网衣结构相互作用的数值模拟。如图7所示，水槽总长14 m，高1.1 m，水深0.86 m，消波区域长2 m，多孔介质区域厚50 mm，多孔介质区域中心距离速度入口7 m，聚焦波聚焦位置位于多孔介质区域中心后方50 mm处，即距离速度入口7.05 m(避免多孔介质区域内部对浪高仪监测的影响)。

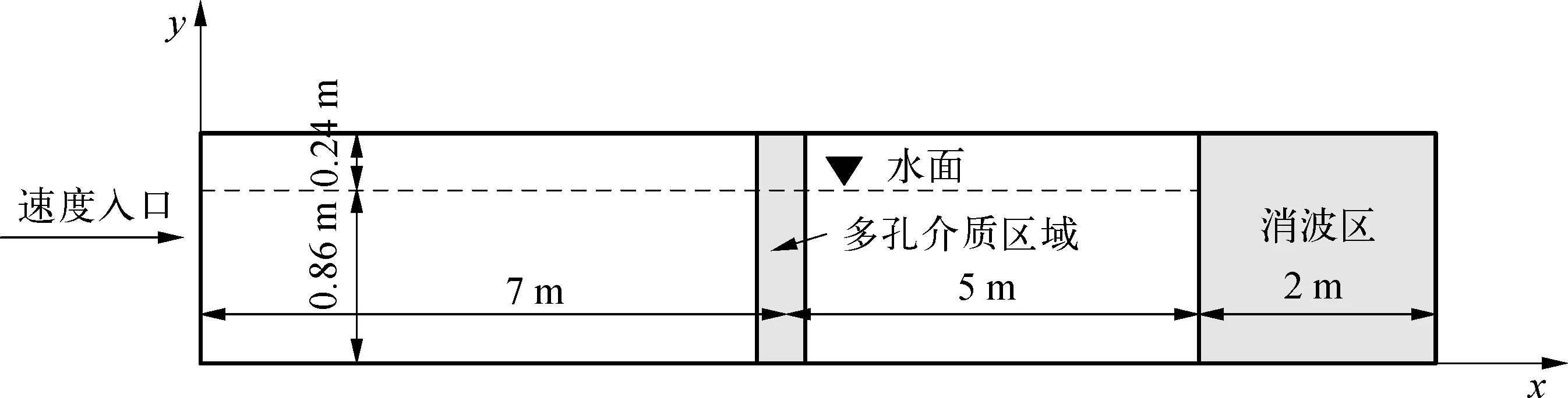
图7 数值波浪水槽

试验中网衣的参数及波浪工况同实际水槽试验，如表1和表2所示，其中聚焦波聚焦位置距造波板7 m。

网格密度按最大波高和波长进行划分，对波浪自由面的网格进行加密，对消波区等区域的网格进行加疏。文中对3种网格类型进行分析，每种网格的具体划分精度见表3。用这3类网格密度对工况Exp_Wave1进行数值模拟，验证其收敛性，数值模拟结果如图8所示。

表3 网格划分精度 Tab.3 Mesh scheme 单位：cm

图8 不同网格的模拟对比

由图8可以得到，随着网格精度的提高，Mesh1和Mesh2的结果有一定差距，但是随着网格继续细化，Mesh3精度并没有显著提高，所以Mesh2满足数值模拟的精度要求，在下文中就以Mesh2的网格精度对聚焦波—网衣结构进行数值模拟。

在数值模拟中，需要与试验一致的参数有密实度Sn(与孔隙率关系为n=1-Sn)，以及在各波浪下网线对应的阻力系数Cd,twine，根据试验的已有数据，数值模拟多孔介质区域所需的参数见表4和表5。

表4 多孔介质阻力系数

表5 多孔介质参数

图9至图12为4个波浪工况下数值模拟和试验结果对比，从中可以得到，数值模拟和试验结果所得数据趋势相同且结果相似，但是可以发现，数值模拟得到的网衣阻力总是大于试验阻力结果，而升力总是小于试验升力结果。这是因为在实际试验中，网衣张紧程度对于网衣受力有影响。在试验中，当聚焦波到达网衣时，网衣由于波浪力发生变形，与波浪传播方向形成一定冲角，从而一定程度上减小了阻力，增大了升力。其次，由于网衣材料的可变性，在网衣张紧状态下其网衣密实度会随网线直径减小而减小。但是在数值模拟过程中，网衣一直处于理想的张紧状态，在波浪下不会发生变形，所以密实度也始终保持一致。

图9 Exp_Wave1波浪工况下数值模拟与试验结果对比

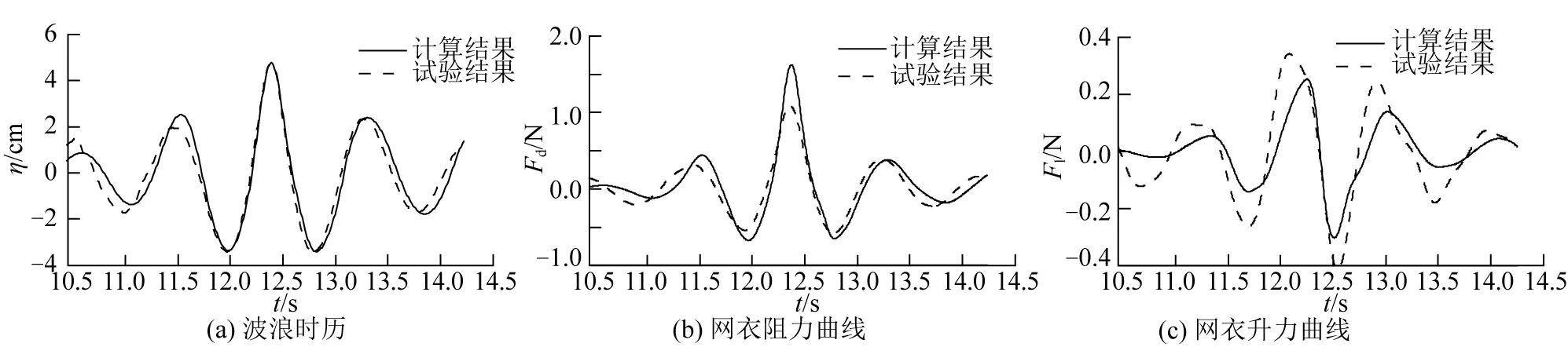
图10 Exp_Wave2波浪工况下数值模拟与试验结果对比

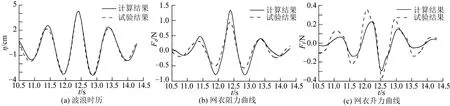
图11 Exp_Wave3波浪工况下数值模拟与试验结果对比

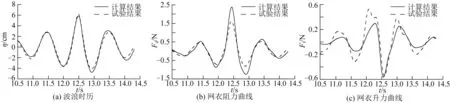
图12 Exp_Wave4波浪工况下数值模拟与试验结果对比

综上，数值模拟结果中网衣阻力偏大且升力偏小是合理的。对比4个波浪条件下的结果，可以验证该数值模型的有效性，能够较准确地模拟网衣在聚焦波下的受力情况。

3 结果与讨论

3.1 网衣密实度对平面网衣水动力特性的影响

本节通过该数值方法研究分析极端波浪下网衣密实度对平面网衣结构水动力特性的影响。以网衣密实度、网线直径、目脚长度为变量设计了12种网衣，具体参数如表6。

表6 网衣参数

其中Net1至Net6通过改变目脚长度来控制密实度；Net7至Net12通过改变网线直径来改变密实度。横向分析两组的水动力特性来比较两种改变密实度的方式对网衣水动力的影响。

在数值模拟中，选取上节的Exp_Wave2聚焦波为模拟工况，表7为具体波浪参数。

表7 聚焦波参数

李玉成等[21]在研究波浪条件下渔网的水动力特性时，分析得到网衣结构在波浪下Morison方程的阻力系数受KC数影响不大，所以在计算网线的阻力系数时，忽略KC数的影响，由此得到多孔介质模型所需的参数，具体如表8所示。

表8 多孔介质模型参数

基于以上获得的波浪参数以及多孔介质参数，在wave2Foam波浪水槽中进行平面网衣的数值模拟，获得各类网衣的水动力特性结果，现对结果数据进行分析。图13(a)和13(b)展示了不同网衣密实度下，经过平面网衣结构后的聚焦波波浪时历，由图可以得到网衣结构的存在影响聚焦波的时空演化，且波浪波幅峰值随着网衣密实度的增大而减少，不过总体上衰减幅度不明显，如图13(a),当密实度Sn从0.05增至0.30，波幅峰值仅从5.04 cm降至4.34 cm，减少了14%。

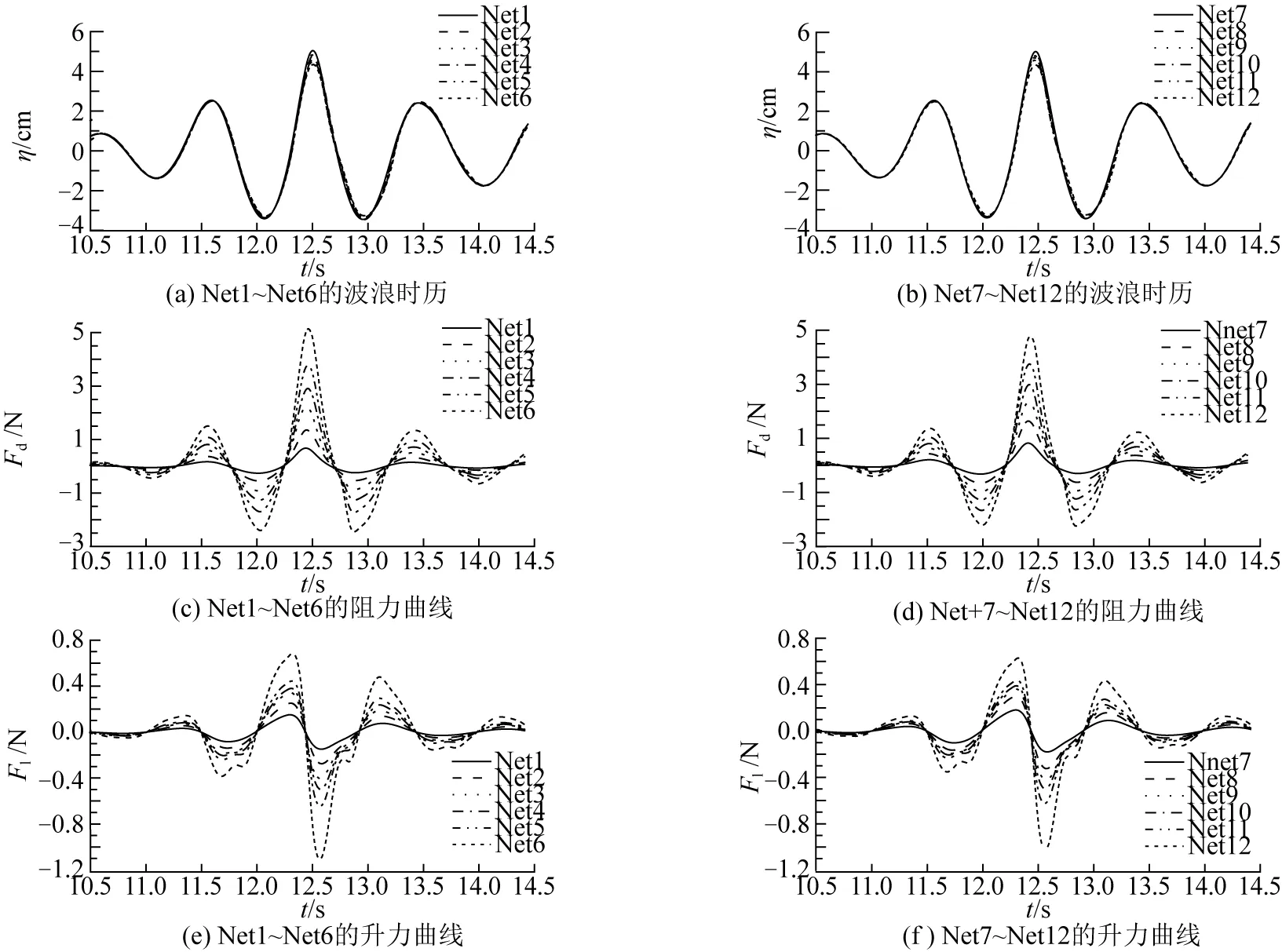
图13 Net1～Net12的水动力特性

图13(c)和13(d)及图13(e)和13(f)证明网衣密实度对网衣的受力有极为显著的影响，总体趋势为网衣受力随着密实度的增大而明显升高。纵向比较图13(c)和图13(e)，发现阻力和升力时历上峰值出现时刻不一致，阻力峰值出现时刻与聚焦波聚焦时刻较为吻合，且阻力曲线左右对称，升力曲线大致为中心对称。这可以根据Morison公式中升力的计算原理进行解释，由于网衣升力大小取决于波浪中水粒子竖直方向上的平均速度，当水粒子水平速度达到最大时，网衣阻力时历的斜率绝对值最小，即此时竖直速度为0；当水粒子水平速度为0时，网衣阻力时历的斜率绝对值最大，此时竖直速度达到极值。比较图13(c)和图13(e)可以证明，升力每个波峰和波谷出现时刻都与阻力为0的时刻相对应，总体上，网衣阻力曲线大致是以聚焦时刻为轴的轴对称图形，升力曲线大致是以聚焦时刻为中心点的中心对称图形，而且当密实度增大时，聚焦时刻前后升力的极值开始不相等，聚焦时刻后峰值绝对值大于聚焦时刻前的峰值绝对值，说明水粒子竖直速度总是在聚焦波到达之后达到最大值。观察图13(e)和图13(f)，发现当网衣密实度增加时，升力时历在受力周期里出现了多个极值，曲线开始不光顺，这是因为聚焦波为强非线性波，当密实度增大，升力整体提高时，高谐波成分对升力的影响逐渐明显。

为了具体分析阻力、升力和密实度之间的关系，就网衣密实度—受力两者进行分析，如图14所示。由图14可以得到，阻力、升力和密实度之间大致成线性关系，如图14(a)所示当密实度从0.05增加至0.30，其阻力峰值从0.68 N增值5.14 N，升力峰值从0.15 N增至0.68 N，阻力升力比也从4.5增至7.5。所以阻力较升力对密实度的变化更加敏感。

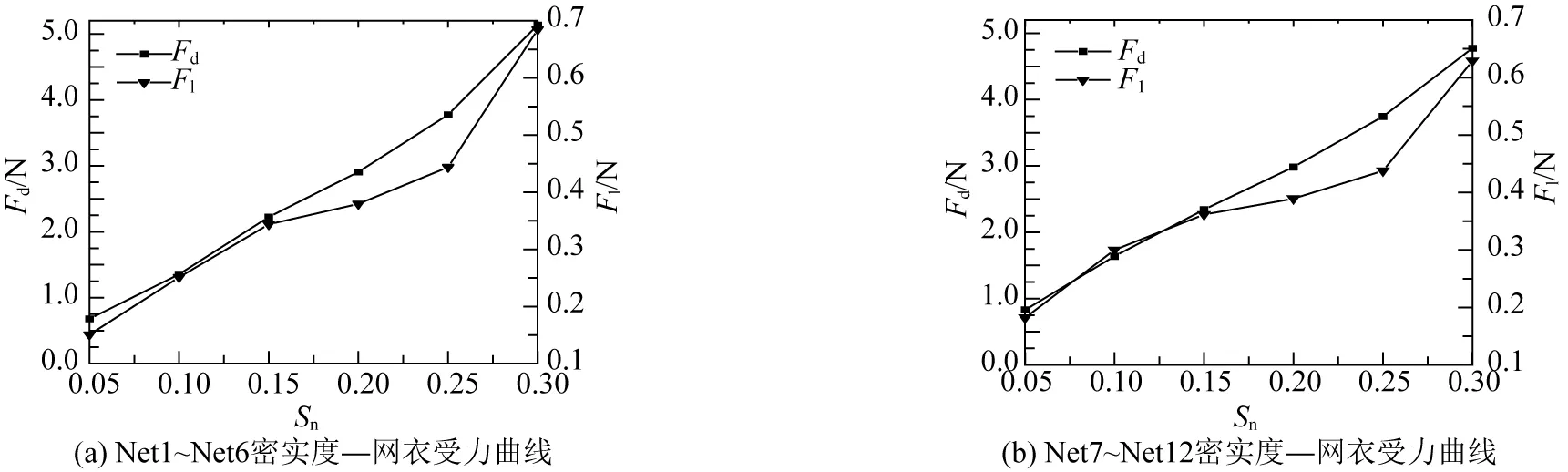
图14 密实度—网衣受力曲线

3.2 聚焦波波幅对平面网衣水动力特性的影响

对平面网衣—聚焦波结构中的聚焦波进行研究，以聚焦波的波幅为控制变量来分析不同聚焦波下平面网衣的水动力特性，探究聚焦波波幅与网衣受力之间的数值关系。网衣选用上节的Net3，根据波幅大小设计6种聚焦波，表9为具体参数。

表9 波浪及多孔介质参数

同理，将各参数代入到数值模型中得到结果，现对结果数据进行处理分析。图15(a)展示了不同聚焦波的波浪时历，波幅从0.83 cm增加至6.61 cm。由图15(b)和15(c)可得，聚焦波波幅的大小对网衣受力有极其显著的影响，总体趋势为聚焦波越大波幅越大，网衣阻力和升力越大。

图15 不同聚焦波作用下网衣的水动力特性分析

为探究网衣受力与波幅之间的具体关系，现对网衣受力峰值和谱峰波幅进行分析，具体如图16所示。由图16(a)可以发现，阻力、升力和最大波幅之间呈非线性关系，且受力增长速率随最大波幅的增加而升高；图16(b)可以得出，阻力与升力之比随着最大波幅的增加而增大，由此推出，最大波幅对阻力的影响较升力更加明显。

图16 波幅峰值—网衣受力曲线和波幅峰值—阻力与升力比曲线

4 结 语

通过网衣试验与数值模拟结果进行对比，验证了数值模型计算的准确性和可行性。其中极端波浪数值水槽基于waves2Foam建立，采用多孔介质模型模拟网衣结构，其多孔介质阻力系数通过与Morison模型计算的网衣受力等效分析的直接估计方法获得。对不同网衣密实度及不同波浪参数下网衣结构的升阻力特性以及网衣结构对波浪场的扰动规律进行分析。得到以下结论：

1)在相同聚焦波下，网衣密实度参数对网衣受力有极为显著的影响，网衣所受阻力和升力随着密实度的增大而明显升高，与密实度大致呈线性关系，且阻力较升力对密实度的变化更加敏感。阻力和升力峰值出现时刻不同，阻力峰值出现在升力斜率最大时刻，升力同理。

2)聚焦波波幅的大小对网衣受力有极其显著的影响，总体趋势为聚焦波最大波幅越大，网衣阻力和升力越大，阻力、升力和最大波幅之间呈非线性关系，且受力增长速率随最大波幅的增加而升高。

3)网衣结构对聚焦波时空演化特征影响相对较小，改变了聚焦波波形，且随着网衣密实度的增大，波浪波幅峰值逐渐减少，不过总体上衰减幅度不明显。