防振锤对深水导管架圆管风致涡激振动抑制研究

2022-10-18张大伟陈佳佳胡文韬刘利琴吴志强

海洋工程 2022年5期

罗超，张大伟，陈佳佳，胡文韬，刘利琴，吴志强

(1.海洋石油工程股份有限公司，天津 300461；2.天津大学，天津 300072)

导管架平台是目前世界上使用最多的一种海洋平台，随着科学技术的发展，其作业水深逐渐加深，达到300 m以上，称为深水导管架平台。由于导管架平台作业水深的增加，使得导管架结构尺寸加大，在一定程度上结构的刚度减小，低阶固有频率降低，更容易发生风致涡激振动[1]，特别是我国海洋环境恶劣，台风频繁[2]，对深水导管架的风致振动及其振动抑制的研究至关重要。

对工程结构涡激振动的控制，有被动控制、主动控制、半主动控制和混合控制4种方法[3]，其中主动控制和半主动控制需要外界能源设备供能，以及传感器等装置，要求复杂。相对而言，被动控制装置设计简单,易于制作、安装和维护,成本较低。防振锤是一种价格相对低廉、装卸方便的被动控制减振装置，其由一根短钢绞线、线夹和悬挂在两端的铸铁锤头组成，如图1所示，最早在电力工程中使用，用于降低导线振动[4-6]。

图1 防振锤

国外关于防振锤的研究起步较早，最早的防振锤由澳大利亚的Bate发明[7]。之后出现了Stockbridge型防振锤，并得到广泛的应用，在此之后的不同类型防振锤基本都是在Stockbridge防振锤的基础上发展而来。Stockbridge最早在工程领域引入了防振锤的概念，早在20世纪20年代Stockbridge就发表了电力行业关于输电线缆风振抑制的第一篇论文，并在理论的基础上发明了著名的Stockbridge型防振锤[8-9]。在此之后，欧美国家开始关注防振锤在导线风致涡激振动抑制方面的应用。20世纪30年代，澳大利亚的Bate首次提出在架空输电线缆上安装防振锤以降低导线疲劳损伤的理论，该理论得到了维多利亚电气委员会(State Electricity Commission of Victoria)的认可[10]。1968年，Salvia发明了沿用至今的FR型防振锤，FR型防振锤具有良好的防振效果和性能，逐渐取代了传统的机械防振锤，并衍生出了FD、FRZ等多型号防振锤，大大促进了防振锤领域的发展[11]。在此之后，Benedettini等[12]，Rega等[13]，Wolf等[14]，Bukhari等[15]，Islam等[16]诸多学者及其团队对防振锤的功率特性、力学结构、共振频率、自阻尼特性、振动抑制等有了较为系统的研究。Vaja等[17]建立了Stockbridge防振锤的有限元模型，对导线—防振锤系统的微风振动特性进行了研究。Diana[18]提出了一种Stockbridge防振锤非线性动力学模型，该模型可针对对称及非对称Stockbridge防振锤进行力学特性分析，并通过试验测量验证了模型的正确性。近年来，人们将这种防振锤用于海洋工程结构的振动抑制。Exxon公司在其Harmony平台和Heritage平台导管架的施工中应用过类似“狗骨头”型的阻尼减振器[19]。我国防振锤主要用于电力行业的导线减振，有关防振锤的设计主要参考国外的公式和方法。

文中将防振锤用于深水导管架的风致涡激振动抑制。建立了防振锤的动力学模型，并研究了其动力特性；将防振锤置于圆管上，建立了圆管的有限元模型，研究了防振锤的减振效果。该工作为防振锤用于深海导管架风致涡激振动抑制设计提供指导。

1 防振锤参数设计

1.1 防振锤动力学模型

防振锤的锤头关于线夹左右对称，建模时可将锤头简化为集中质量[20]，线夹出口处理为固定支撑，钢绞线处理为弹簧，忽略钢绞线的质量和惯性，模型有2个自由度。锤头质心竖直方向的振动用y0表示，绕质心的转动用φ0表示，如图2所示，其中，O为锤头质心，O′为钢绞线与锤头连接点；s为钢绞线锤头连接点与质心之间的距离；L为固定端与钢绞线锤头连接点之间的距离。

图2 防振锤模型简化

根据刚体平面运动理论，钢绞线与锤头连接点O′的位移可以用质心O的位移来表示：

y0=y0′-sφ0′

(1)

φ0=φ0′

(2)

忽略钢绞线的质量和惯性，因此系统的动能可以表示为：

(3)

式中：M和J分别表示锤头的质量以及相对于质心的转动惯量。

系统的势能可由钢绞线的弯曲应变能表示：

(4)

其中，EI表示钢绞线的刚度，钢绞线上的弯矩M(x)可表示为：

M(x)=F0′x+M0′

(5)

其中，F0′为作用在锤头端部的惯性力，M0′为作用在锤头端部的惯性力矩，可以通过悬臂梁的变形公式表示：

(6)

将式(6)代入式(4)、式(5)，得到最终势能表达式为：

(7)

在不考虑系统阻尼的情况下，可通过拉格朗日方程列出该2自由度系统的运动微分方程：

(8)

L=T-U

(9)

(10)

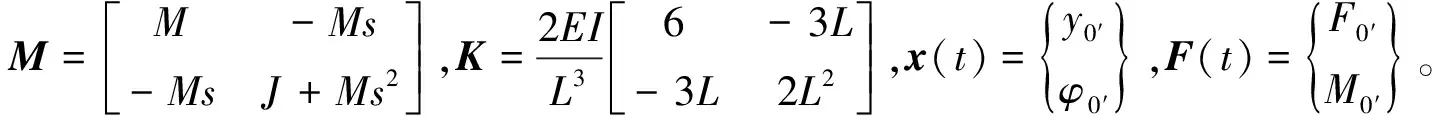
在系统自由振动时，外力向量为0。假设微分方程的解为：

(11)

式中：ω和α分别为系统的固有频率和相角。将方程的解代入式(10)并使外力向量为0可得：

(12)

使y0′和φ0′取得非零解的充要条件是系数行列式为0，进而推导出集中质量模型频率方程的求解方程为：

|-ω2M+K|=0

(13)

式(13)中的刚度矩阵K和质量矩阵M可以由防振锤的相关结构参数决定，通过求解行列式得到前两阶固有频率。合理地进行结构参数设计，可以尽可能使防振锤与圆管固有频率接近从而达到更好的减振效果。

1.2 防振锤功率特性曲线

由1.1节推导可知，有阻尼防振锤强迫振动的微分方程为：

(14)

(15)

可将各个位移改写成振幅的复数形式：

(16)

将式(6)代入式(14)得到防振锤振幅为：

x=(-Mω2+K+iωC)-1F

(17)

(18)

进一步计算图2中固定端的约束力，并且求得整个系统的功率为：

F0=k11y0+k12φ0

(19)

(20)

式中：k11和k12为刚度矩阵K的下标元素。可由阻抗求出式(20)中系统的相位差θ为:

(21)

通过分析，计算出适合文中的8 Hz防振锤参数如下：单个锤头质量3.8 kg，钢绞线长0.52 m，钢绞线直径0.013 m。根据以上参数及推导公式，绘制出防振锤的功率特性曲线如图3所示。由图3可以看出，设计的防振锤有2个频率峰值8 Hz和28 Hz。

图3 防振锤功率特性曲线

2 防振锤减振效果数值分析

2.1 结构建模

以中国南海某深水导管架为例进行分析。通过规范筛选出一根易发生涡激振动的圆管，以该管为例进行分析。管的参数为：管长21.49 m；直径0.762 m；管厚0.016 m；弹性模量2.1×1011N/m2；泊松比0.3；阻尼比0.001 5；密度7 850 kg/m3。防振锤沿管道轴线顺向布置，这种布置方式对管道四周的空间影响较小，以减小防振锤安装对其他作业的影响；此外，顺向布置方便在管道同一截面上安装多组防振锤，减振效果更好。

ANSYS软件是目前世界上通用的结构分析软件，在很多领域中广泛应用，具有极强的建模分析能力，能够进行精细的结构分析，文中采用该软件建立固支圆管模型，并进行数值模拟。采用Pipe288单元模拟圆管，模型相关尺寸根据给定数据建立。对防振锤子系统结构进行简化，采用Mass21单元模拟锤头，赋予其在竖直方向(y轴方向)运动的质量；再采用Beam188单元模拟钢绞线，根据给定数据定义其横截面的实常数：截面积和惯性矩。由于锤头的质心与钢绞线的连接点存在一定的偏心距，因此采用长度等于偏心距，刚度比前面的梁单元大3个数量级的Beam188单元将锤头的质量单元和钢绞线梁单元连接[21]。

根据规范OTC—6902[22]可以设计出防振锤的安装数量。根据规定的稳定性参数最小值，可以计算出结构所需的最小阻尼比，从而推算出所需防振锤的数量。所允许的最小稳定性参数表达式为：

(22)

其中，CL为升力系数；γi为模态形状因子；ηmax为圆管直径方向允许的最大响应，表达式为：

(23)

其中，Sp为热点应力范围；E为弹性模量；Fi为张紧相应参数；αSCF为应力集中系数；L为圆管的长度；D为圆管的直径。模态形状因子γi和张紧响应参数Fi与圆管约束形式有关，具体取值见文献[22]。

根据最小稳定性参数就可以计算出结构所需的最小阻尼比为：

(24)

式中：ρa为空气密度；me为圆管单位长度质量。

在圆管上添加防振锤后，有效阻尼比的增量为：

(25)

式中：N为防振锤数量，取偶数；Cd为黏性阻尼系数，取270；me为圆管单位长度质量；fn为固有频率；λ为振型因子，一般取0.4。

若要使得圆管稳定性参数符合规范要求，则防振锤数量应满足ξe+ξp>ξmin(ξp为未添加防振锤时圆管的有效阻尼比)。将圆管相关参数代入上述公式得到防振锤所需数量为4。最终建立的有限元模型如图4和图5所示，4组防振锤的编号见图5。在固定端节点加上全部自由度的约束，进行模态分析，得到圆管的各阶固有频率及固有振型，前四阶固有频率为10.374 Hz、28.205 Hz、54.419 Hz、74.756 Hz。结构的阻尼根据瑞利阻尼输入[23]。导管架圆管发生风致涡激振动时，主要涉及第一阶和第二阶的固有频率，若圆管阻尼比为0.001 5，则得到瑞利阻尼的系数α=0.022 6，β=0.000 078。

图4 圆管有限元模型

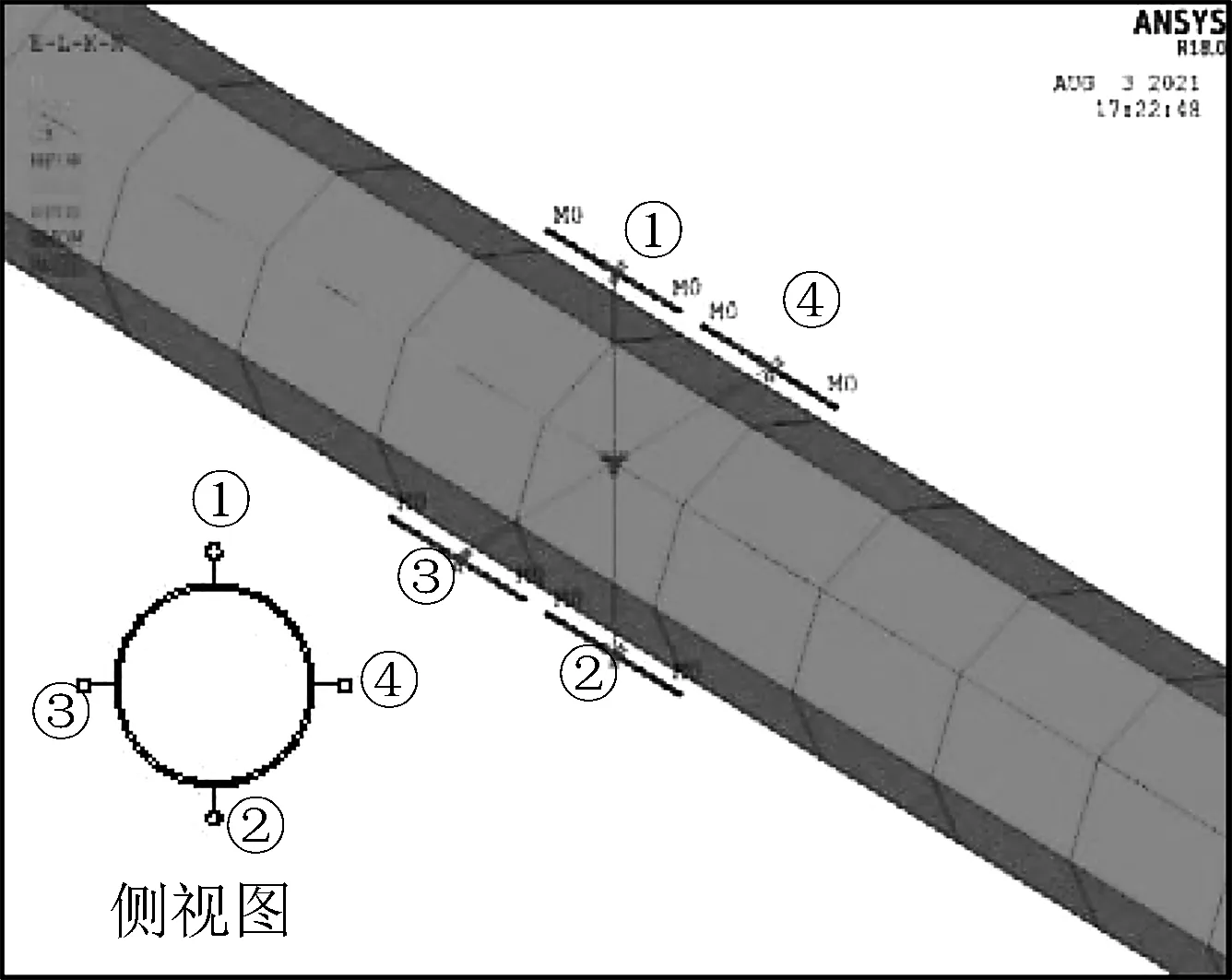
图5 防振锤布置有限元模型

2.2 防振锤减振效果分析

根据共振条件可知当涡泄频率接近结构一阶固有频率时发生锁频现象。涡泄频率公式为：

(26)

根据文献[22, 24]取St=0.21，估算出风速U=37 m/s下固有频率与涡泄频率接近，将涡激力处理为强迫激励[25]均匀施加在圆管上，激励幅值为：

(27)

式中：ρa为空气密度，取1.19 kg/m3；CL为升力系数，取值为0.158。

将涡激力以均布力的形式施加在圆管上进行时域计算，提取圆管中点的结果，对比加防振锤和不加防振锤圆管中点处的振动响应，结果如图6所示。

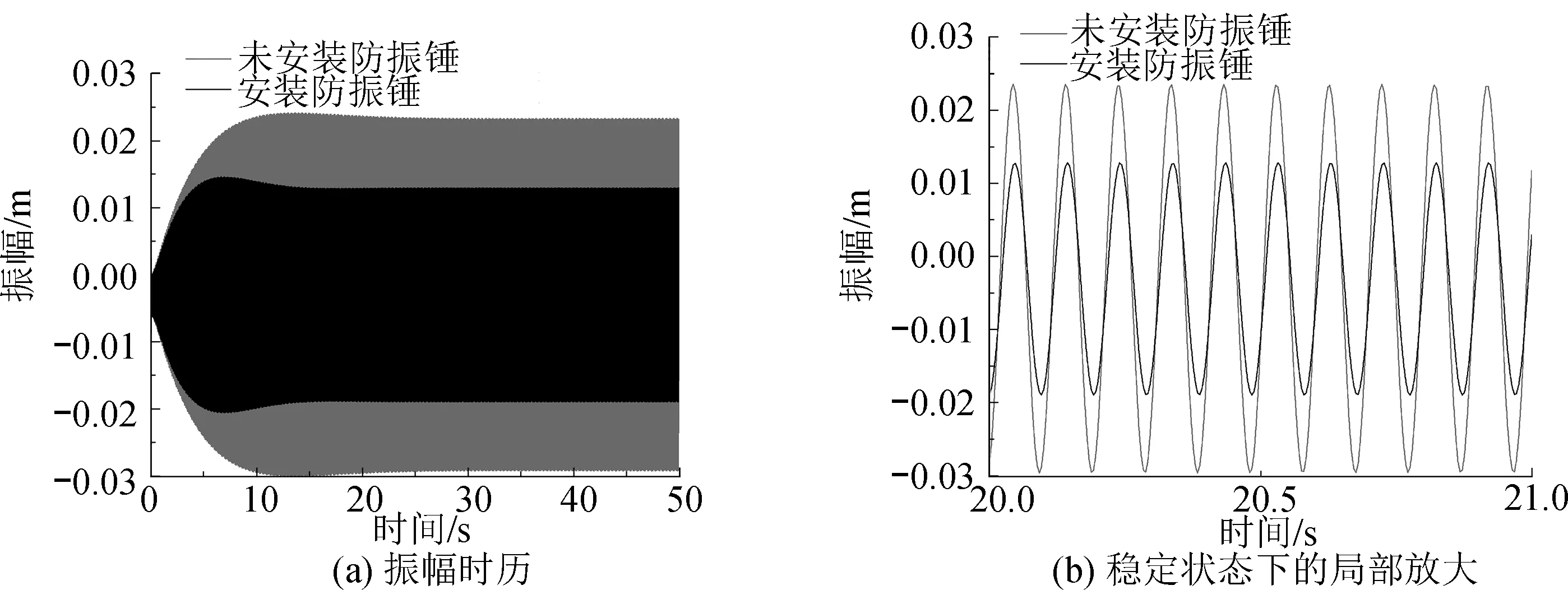
图6 圆管振动响应对比

由图6可知，在涡激力的作用下，未安装防振锤时，圆管中点的响应幅值为2.36 cm，安装防振锤后的振动幅值减少到1.25 cm，减振效果达到47%，因此文中设计的防振锤具有很好的减振效果。图7给出涡激力作用下，安装在圆管上的锤头①上的振动响应。可以看出，锤头振幅接近2.5 cm，在圆管发生涡激共振后，圆管能量会通过连接件传递给钢绞线和锤头，致使锤头发生剧烈振动。因此，在对防振锤支撑结构进行设计时，锤头与圆管的距离要大于2.5 cm。

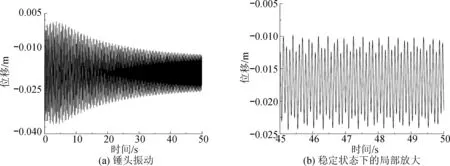
图7 防振锤锤头振动响应

3 基于实际测试的数值结果验证

为进一步验证数值分析方法的正确性，对实际管道的减振效果进行了测试验证。测试的管道参数为：外径168 mm，壁厚14 mm，管长10 m。采用偏心电机进行激振，用加速度传感器测试管道振动；在管道上加一个8 Hz防震锤，如图8所示。

图8 减振效果试验测试

对测试管道进行有限元建模，模拟与试验相同激励下管道的振动响应，并与试验结果对比，如图9和图10所示。对结果进行统计，得到不同工况管道的响应幅值，并进行对比，结果如表1所示。

图9 减振效果对比(激振转速320 r/min)

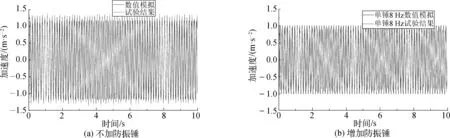
图10 减振效果对比(激振转速400 r/min)

表1 不同工况振动幅值试验数值对比

以上分析表明，数值模拟与测试结果非常接近，但无锤工况的误差大于有锤工况的误差，这主要是由偏心电机的激励误差引起。没有安装防振锤时，管的振动较大，对偏心电机激励力影响较大，导致数值结果和测试结果相差较大；安装防振锤后，管的振动较小，对偏心电机激励力影响较小，数值结果和测试结果相差较小。但总体上差异在15%以内，验证了数值分析方法的有效性。