基于无网格MPS方法数值分析方舱破舱进水问题
2022-10-18卢泽宇万德成
卢泽宇,万德成
(上海交通大学 船海计算水动力学研究中心(CMHL)船舶海洋与建筑工程学院,上海 200240)
伴随着经济全球化和地区贸易自由化,航运业也得到快速发展,然而多种多样的海难事故,例如着火或爆炸、进水、碰撞、搁浅、倾斜或倾覆、沉没、失控及漂浮等,造成了严重的经济损失,对人员的生命安全也造成了严重威胁[1]。海难事故导致的受损船舶水密舱室进水也一直是行业关注的焦点,众多学者对其进行了研究。受损船舶的水密舱室进水可能会严重影响船舶的稳性并威胁其安全。水的快速流入可能导致大振幅的船舶运动从而导致倾覆,研究的目的是对进水过程中二维受损舱段的运动特性进行数值模拟分析。
按照时间顺序,船舶受损后,如图1所示,进水过程主要分为3个阶段,瞬时进水阶段、持续性进水阶段和稳定阶段[2]。在大多数损坏情况下,瞬时进水阶段会引起受损船舶大幅度横摇,但持续时间较短,这使得该阶段往往是最危险的阶段;稳定阶段持续时间较长,但船舶横摇过程较平缓;持续性进水阶段需要更长的时间才能使受损船舶达到新的平衡状态。
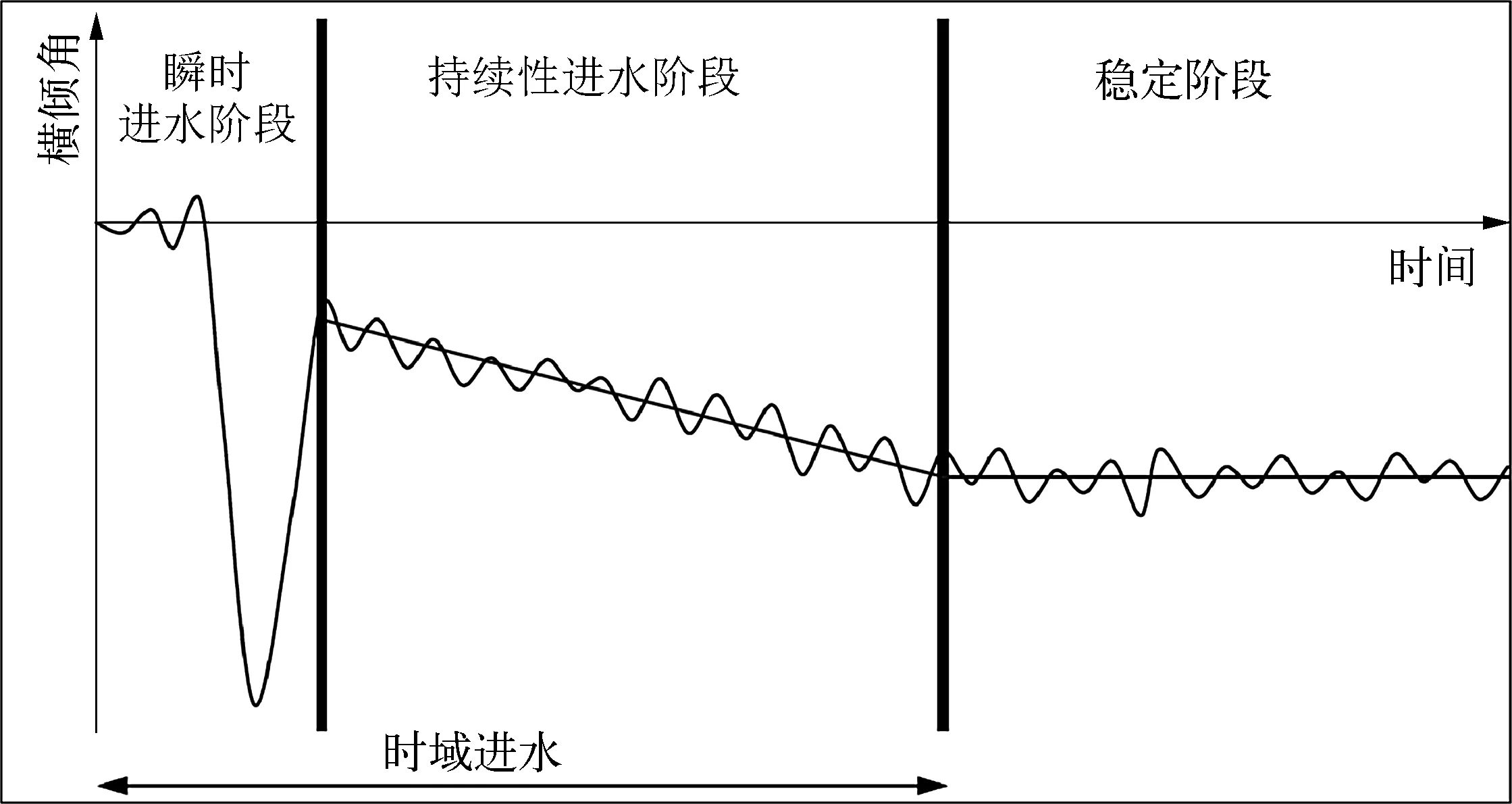
图1 进水过程的主要阶段
因此,目前的研究大多数集中在持续性进水阶段[3]。由于静态方法过于简单,无法应用于持续性进水阶段,许多学者采用准静态方法进行持续性进水阶段的模拟[4]。Papanikolaou等[5]和 Jasionowski[6]考虑了进水的影响。为了研究破舱的过程,Palazzi和De Kat[7]将空气和水看作是在一定范围内机械运动的集中质量块,一定程度上,这种假设更接近于受损船舶运动的模型试验结果。Ruponen[8]通过时域浸水分析,研究了非水密结构对典型现代大型客船持续进水和倾覆时间的影响。Lee[9]还提出了通风隔间的新模型和蓄能器模型,以研究复杂的开口系统对持续进水过程中水流和空气的影响。以上研究都基于准静态假设,计算成本相对较低。然而,进一步的研究表明,舱内的流动确实会影响船舶的瞬态运动特性,使用简化的准静态模型难以对问题进行综合考虑。因此,研究人员开始探索其他方法。
Manderbacka等[10]提出了一种全耦合方法来研究船舶对瞬时进水的响应,其中考虑了传递动量的进水入口,并通过进水船舶的横摇阻尼和瞬时进水试验数据验证了该方法。Acanfora和Cirillo[11]通过将准静态方法与完全耦合方法耦合开发了一种中间方法,不再假设自由表面是水平的,并且平面的倾斜角取决于船的水平加速度,将模拟数据与驳船模型的试验测量值进行比较并得到了验证。Manderbacka和Ruponen[12]通过比较全动态和准静态洪水模拟,对瞬时进水的水动力学进行了研究,通过改变舱壁开口的大小来评估进水射流对船舶响应的影响。一些研究人员依靠模型试验来评估受损船舶运动的高度非线性进水过程。Zhang等[13]的试验考虑了两种带有舷侧开口和底部开口的船舶模型,以证明损坏对船舶失稳和沉没时间的影响。Gu等[14]试验研究了完整和损坏的战舰 DTMB-5415 在波束中的性能,表明海水的进出及其与船舶运动的相互作用显著影响船舶上受到的冲击载荷。
当前试验方法存在局限性,例如难以对整个流入区域的数据进行全面监测,试验准备成本高且复杂等。近年来,计算机计算能力的提高使得船舶水动力响应的数值模拟变得容易。Gao和Vassalos[15]使用基于雷诺平均N-S方程(RANS)的计算流体动力学(CFD)求解器和基于自由表面的流体体积(VOF)方法来研究液舱晃荡和进水对损坏船舶水动力学的影响。Cao等[16]开发了一个三维并行光滑粒子流体动力学(SPH)程序来模拟具有舷侧和底部开口的模型下沉过程,以研究船舶的稳定性和下沉时间。为了揭示破舱水动力学与波浪中受损船舶之间的相互作用,Gao和Vassalos[17]使用结合了耐波求解器和 Navier-Stokes 求解器的集成方法来模拟滚装渡轮在规则波中的运动,发现受损船舶的自然横摇频率变化和横摇响应降低主要是由浸水舱室内的水晃动所致。
近些年的研究主要集中在持续性进水阶段,很少有研究考虑过瞬时进水。事实上,瞬时进水期间的大角度横摇可能会导致受损船舶倾覆。因此,为了评估这一瞬时进水阶段,对受损船舶进行可靠的数值模拟是必要的。Manderbacka等[10]提出了一种用于受损船舶运动的非线性时域仿真方法,并研究了两种不同的初始稳定性条件、两种不同的舱室布局以及黏性阻尼的影响。此外,现有研究还表明,不应忽视破舱进水流量的影响。而使用粒子法的优点是可以准确地捕捉自由面的剧烈变形,因此,已被广泛用于模拟液舱晃荡、溃坝流、物体入水、甲板上浪、波物相互作用等剧烈流动问题。张雨新等[18-19]采用MLParticle-SJTU程序对二维和三维液舱晃荡问题进行了模拟,计算的壁面砰击压力和自由面波形与试验和其他方法结果吻合。Zhang等[20]使用改进的MPS方法对二维损坏船段进行了不同开口和挡板的数值模拟,并对进水量等物理量进行了分析。田鑫和万德成[21]采用MLParticle-SJTU程序对逐渐溃坝的问题进行数值模拟,研究了坝体不同失效时间对溃坝流动以及砰击压力的影响。Xie等[22]基于自主开发的软件MPSGPU-SJTU研究了方形液舱内晃荡的三维效应。Wen等[23]在改进的MPS方法基础上,进一步发展形成了具有高精度和高稳定性的多相流MPS方法,并结合多CPU 并行加速技术和GPU并行加速技术,开发了拥有独立自主知识产权的高性能多相流求解器软件MMPS,随后,成功将文中方法和求解器应用于多个典型多相流问题,包括含复杂界面的气泡流问题,船海工程中内孤立波问题,以及剧烈两相晃荡和溃坝问题。
本文简要介绍了改进的MPS方法数值模型,MPS方法通过与SPH方法和VOF方法进行对比得到验证,最后给出数值模拟模型的参数和不同的横截面模型,比较了受损舱段截面各种模型的破舱进水情况。
1 数值方法
从核函数、压力梯度模型、压力泊松方程源项以及自由面判断等方面入手,对MPS方法进行了一系列改进,并在单相流问题中取得了比较好的应用成果。这里将对MPS方法基本格式进行介绍。
1.1 控制方程
对于不可压缩黏性流体,MPS方法控制方程包括连续性方程和N-S方程,其形式为:
(1)
(2)
式中:D/Dt表示物质导数,t为时间,ρ为流体密度,P为压力,μ为动力黏性系数,取1.01×10-5,V为速度矢量,FV为体积力。可以注意到,在MPS方法中,动量方程左侧的时间导数项以物质导数形式给出,因此有效避免了对流项带来的数值耗散。
在无网格粒子类方法中,整个计算域通过对一系列空间粒子进行离散,并根据粒子间相互作用对上述控制方程进行求解。但由于此类方法中的粒子可自由运动,使粒子间拓扑关系变得不固定,因此需在每步计算中进行邻居粒子搜寻和配对,并对不同粒子间的相互作用大小进行评估。为此,MPS方法中引入了核函数及粒子相互作用模型的概念。
1.2 MPS核函数
核函数(kernel function)在无网格粒子类方法中起到权重函数的作用。一般而言,当粒子间距离大于一定范围时,核函数的值为0,即该对粒子之间不发生相互作用。随着两个粒子不断靠近,核函数的值逐渐变大,粒子间的相互作用也变得更强,反之亦然。与SPH 方法不同,MPS方法中并不要求核函数光滑可导,因此核函数形式更简单,也更多样。张雨新和万德成[18]提出一种无奇点的核函数,形式为:
(3)
式中:re为粒子作用半径,r为相邻两个粒子的距离。通过Koshizuka和Oka[24]的数值研究,通常对拉普拉斯模型的作用半径re1取4.01l0,对粒子数密度模型、梯度模型、散度模型和邻居粒子分布函数模型的作用半径re2取2.1l0,其中l0为初始粒子间距。
1.3 粒子相互作用模型
基于上述核函数,可对某一目标粒子受到的所有邻居粒子作用进行加权平均,并推导得到一系列的粒子相互作用模型。利用这些模型,最终实现对控制方程中多种微分算子的离散和求解。MPS方法中所采用的粒子相互作用模型,主要包括梯度模型、散度模型和拉普拉斯模型,分别为:
(4)
(5)
(6)
式中:P为压力,V为速度矢量,φ代表任意标量,D为空间维度,r为粒子位置矢量。n0为初始粒子数密度,用来表征流体粒子分布的疏密程度,如式(7)。λ是对用有限范围的核函数来代替无限范围的高斯函数带来误差的一种补偿,可用式(8)计算得到。
(7)
(8)
1.4 压力泊松方程
MPS方法的流场压力是通过压力泊松方程计算得到,Tanaka 和Masunaga[25]结合粒子数密度和速度散度,提出了一种混合源项的压力泊松方程,如式(9)。
(9)
式中:Δt为时间步长,n*为临时粒子数密度,V*为粒子临时速度矢量。根据Lee等[26]的研究,γ通常取值为0.01~0.05。
1.5 固体壁面和自由面边界条件
在泊松方程求解时,自由面粒子和第二类边界粒子的压力被赋值为0作为方程的边界条件,因此需要正确判断出自由面粒子。如图2所示,对于单相流MPS方法,并不考虑气相和液相之间的相互作用,没有粒子表示气相介质,因此原本的气液两相交界面就是流体相的自由液面,并且自由面附近流体粒子的邻居粒子基本分布在一侧。基于这种粒子分布的不对称性,张雨新和万德成[18]定义了一个衡量邻居粒子不对称性的矢量:
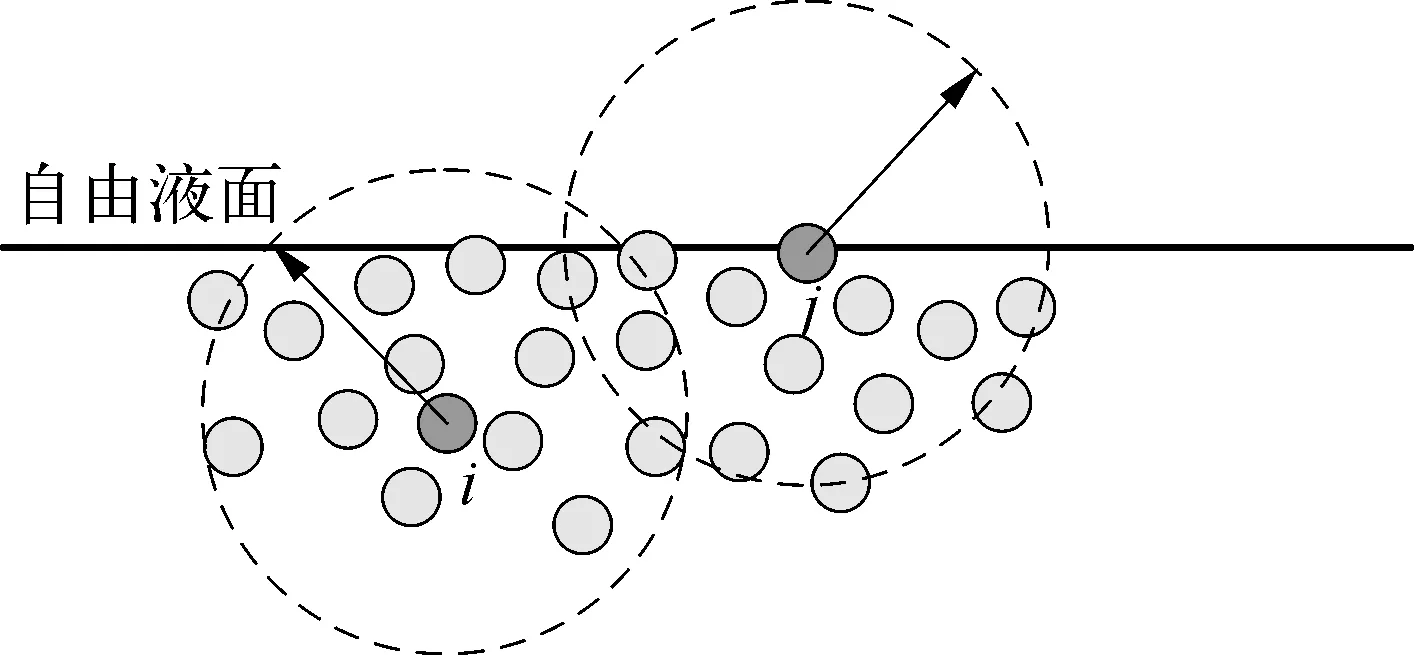
图2 邻居粒子分布
(10)
当粒子满足式(11),该粒子则被判断为自由面粒子。
|F|>α|F|0
(11)
式中:|F|0为初始时刻自由面粒子的|F|值,α为常数。经过张雨新和万德成[18]的数值研究,α建议取值0.9。
MPS方法采用布置多层粒子的策略作为物面边界条件,在物面上布置一层粒子称为第一类边界粒子,然后在第一类边界粒子之外再布置两层第二类边界粒子,如图3所示。其中,第一类边界粒子的压力和流体粒子一起参与压力泊松方程求解,第二类边界粒子的压力通过第一类边界粒子和流体粒子的压力插值得到。这种多层粒子布置方式克服了在物面附近发生积分域的截断,引起数值结果失真问题,还避免了流体粒子在边界粒子运动时穿透物面。
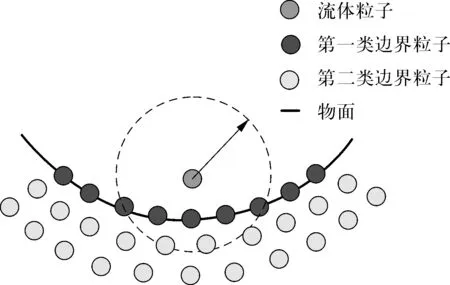
图3 边界粒子分布
2 结果与讨论
2.1 数值模型验证
为了证明模型的可行性,采用基于GPU的MPS方法来模拟二维方舱舷侧上部开口的破舱进水过程,与Shen等[27]使用VOF和SPH方法的模拟结果进行比较。
如图4所示,模型为边长0.1 m的正方形舱,舷侧上方有一个0.02 m的开口,在计算域内模拟静水下的破舱进水,其参数如表1所示。
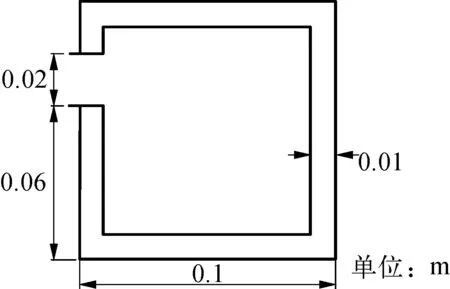
图4 模型尺寸示意

表1 方舱参数
模拟过程如图5所示,从上到下分别是VOF、SPH、MPS方法,从左到右分别是在0.1 s、0.2 s、0.3 s、0.4 s时刻的模拟。可以看出在各个时刻3种方法的模拟现象基本一致。

图5 3种方法在不同时刻的模拟
将模拟结果与SPH方法对比如图6所示,可以看出文中所用MPS方法在横荡和垂荡上的加速度与SPH方法的结果拟合较好。
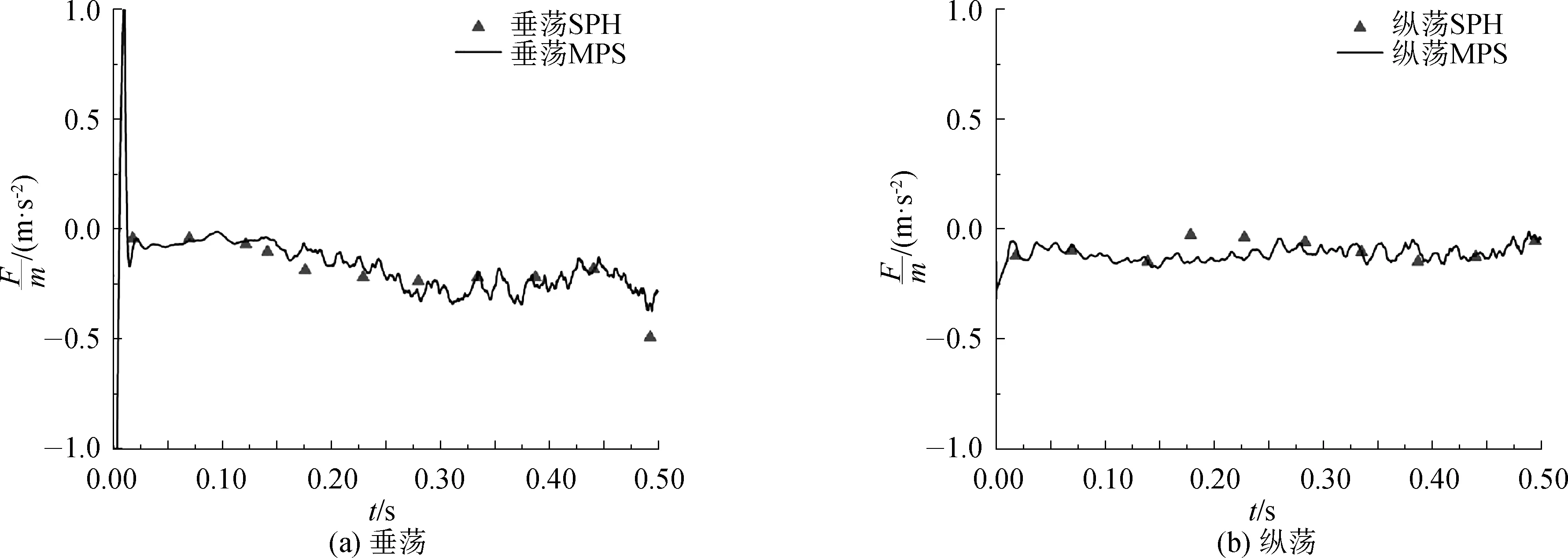
图6 两种方法的纵荡和垂荡模拟结果对比
2.2 横截面模型
为了系统地研究不同破舱场景下的影响,文中模拟了受损舱段在破舱进水后的运动响应,在其舷侧上的关键位置开孔来表示船体损坏。在受损船段内使用非穿透性挡板进行进一步的模拟。舱的尺寸在上一节中有介绍,开孔位置以及舱内挡板分布如图7所示。初始粒子间距为0.05 mm,时间间隔为0.000 01 s。对于A1模型,粒子总数为328 738个,其中流体粒子289 750个,壁面粒子为13 500个,每个时间步的计算时间约为30 s。其他模型的粒子数量和计算时间大致相同。
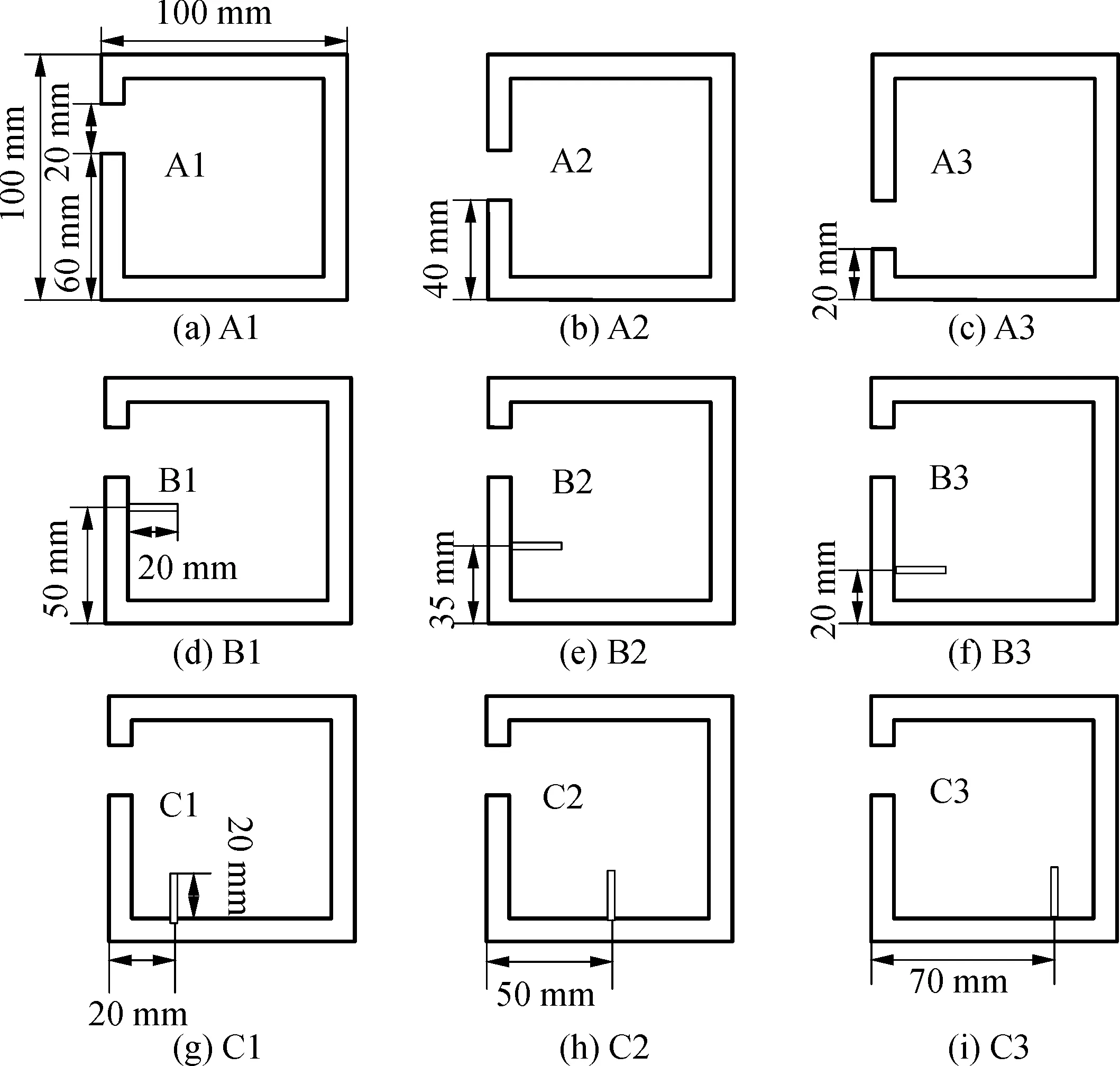
图7 横截面模型的9种配置
2.3 开口位置对破舱进水的影响
图8(a)绘制了模型A1、A2、A3的进水量N的时间历程。可以看出,损坏孔的位置对进水速率的影响较为显著。一般来说,水面以下距离水面较远的受损孔洞会导致更大的进水量,这是由于距离水面越远水压越大,会迫使更多的海水涌入舱室。
图8(b)可以看出进水导致舷侧开口模型A1、A2和A3向损坏侧水平移动。位移在达到峰值后,由于右侧反射回来的流体冲击左侧舱壁导致位移回调。从图8(c)可以看出,开口位置越低,下沉速率越快,与进水速率成正相关。
图8(d)表明,开孔的位置显著影响了横摇运动。A1位置的开口由于压力缺口导致舱左倾,而A2、A3开口由于入射水柱的冲击力更强,进水量更大,导致初始阶段产生右倾。同时可以看出开口位置更靠下部的A3比A2对右倾的影响更大,和进水量成正相关。
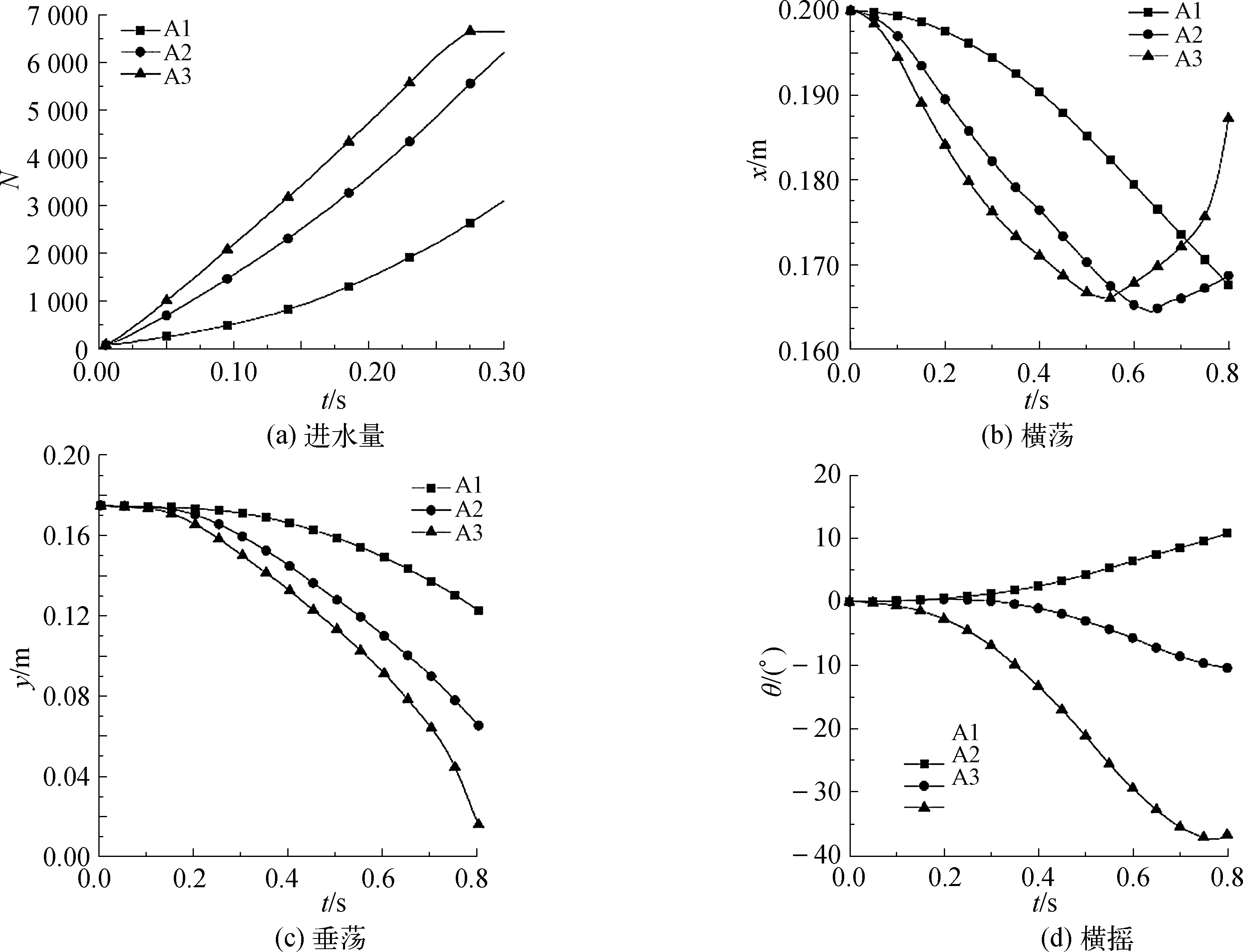
图8 舷侧不同开口位置模型的进水量、横荡、垂荡和横摇时域历程
图9展示了A2模型破舱进水的过程,从图中可以看出,损坏开孔位置对流体的流动特性也有显著的影响,并在舱室内产生涡流。
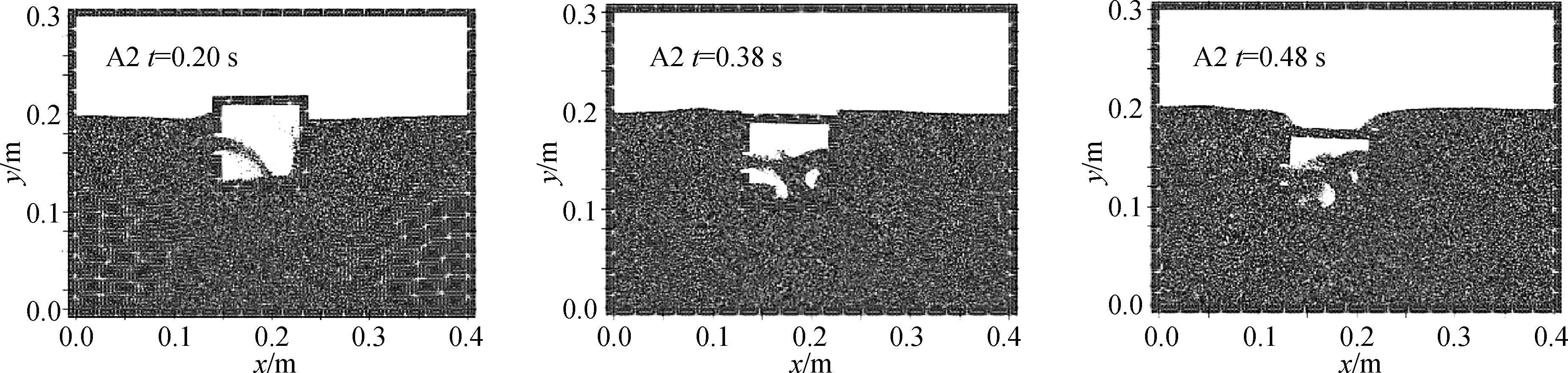
图9 模型A2的舷侧开口引起的进水过程屏幕截图
2.4 水平挡板对破舱进水的影响
为了研究障碍物对受损舱段截面模型相关运动响应的影响,在船截面模型B1、B2、B3和C1、C2、C3内分别设置了非穿透性水平和垂直挡板,如图7所示。
图10(a)绘制了带有水平挡板的模型进水量N的时间历程。由图可知,这些模型的进水量在同一时刻几乎没有差别。也就是说,流入速率之间的差异仅随时间略微增加。说明水平挡板位置对进水量的影响有限。
图10(b)、10(c)、10(d)分别绘制了带有挡板的模型B1、B2、B3引起的横荡、垂荡和横摇运动时间历程。如图所示,在不同位置布置水平挡板对横荡和垂荡的影响差异很小而对横摇的影响差异很大,且随着时间增加这种差异会越来越大。在远离开口位置附近布置水平挡板对横摇的改善明显要优于开口位置附近布置水平挡板。在t=0.8 s时,上部水平挡板模型(B1)的横摇角度与下部水平挡板模型(B2)相差近40%。
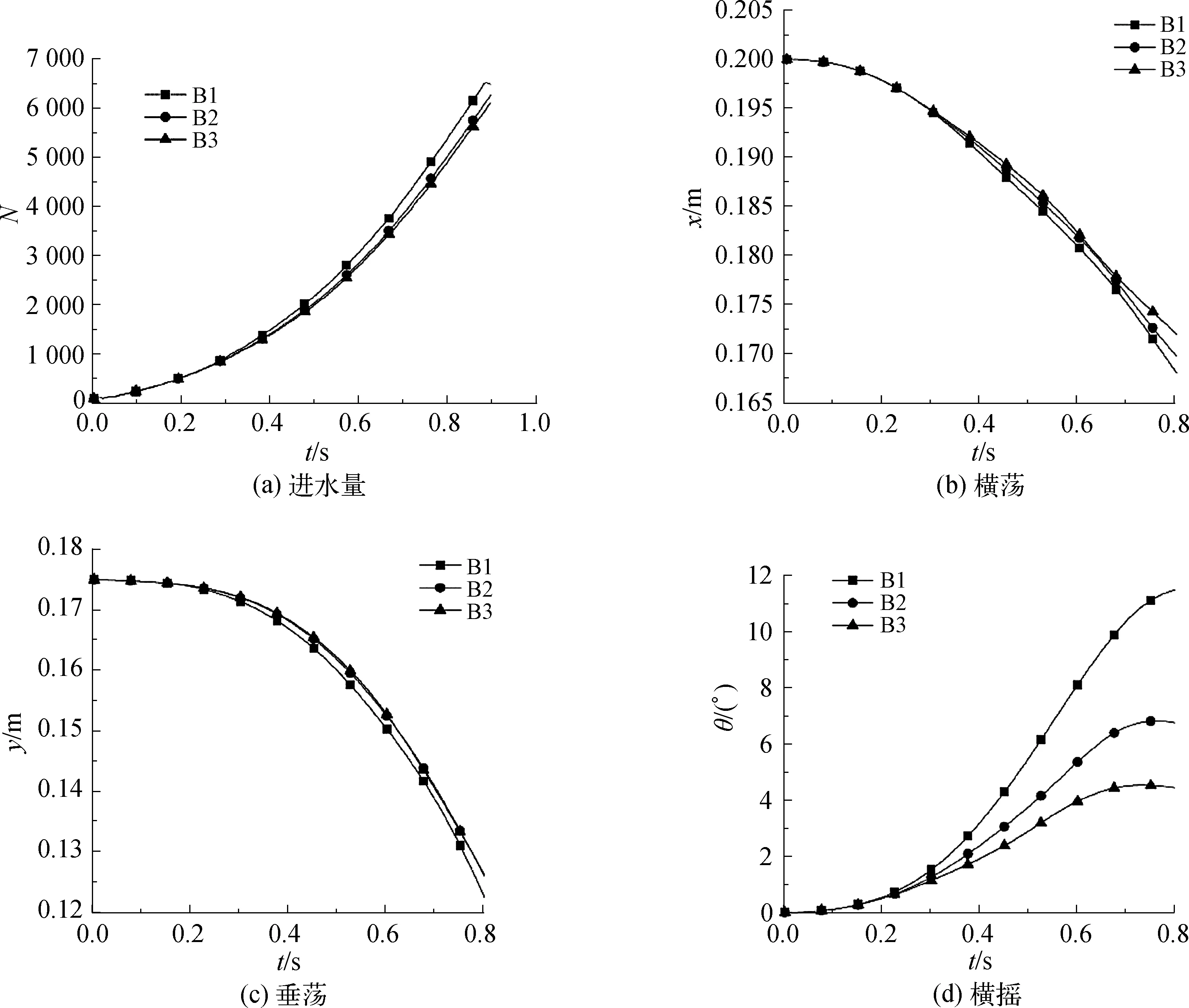
图10 舱内不同位置水平挡板模型的进水量、横荡、垂荡和横摇时域历程
2.5 垂直挡板对破舱进水的影响
图11(a)绘制了带有垂直挡板的模型进水量N的时间历程,如图所示,垂直挡板远离开口位置的模型进水速率更快。产生这种现象的原因是垂直挡板阻止了初始入射流扩散到远离损坏侧的区域,导致更大的横摇力矩和更剧烈的横摇运动(如图12所示)。
图11(b)、11(c)、11(d)分别绘制了带有挡板的模型C1、C2、C3引起的横荡、横摇和垂荡运动的时间历程,如图所示,在不同位置布置竖直挡板对横荡和垂荡的影响差异很小而对横摇的影响差异很大,且随着时间推移这种差异会越来越大。垂直挡板影响了初始入射流的分散,导致更剧烈的横摇运动。在t=0.8 s时,最右边垂直挡板模型(C3)的横摇角度与最左边水平挡板模型(C1)相差近30°。
图12展示了模型B1、B2、B3(带水平挡板)和模型C1、C2和C3(带垂直挡板)的破舱进水过程中在时间t=1.1 s时的压力云图。可以看出,垂直挡板对破舱内流动的影响大于水平挡板,表明挡板的位置和形式会对破舱后的运动响应有影响,特别是对横摇运动产生很大影响。
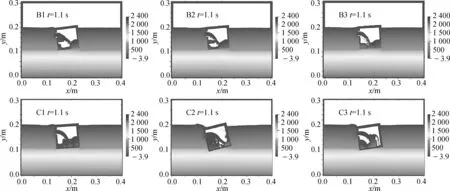
图12 带挡板方舱破舱进水过程在t=1.1 s时刻的压力云图
3 结 论
本文数值模拟了静水条件下沉没过程中受损二维方舱舱段模型的进水及其相关运动。首先,为了满足数值计算的需要,选用基于GPU加速技术的MPS方法。通过与以往其他数值结果的对比,证明该模型的准确性,适用于研究自由漂浮二维破损舱段的瞬时进水过程。其次,对该方舱的各种模型进行了数值模拟。这些模型由方舱舱段横截面组成,其舷侧不同位置有开孔,同时在内部布置水平和垂直的非穿透性挡板。通过数值模拟分析,得出以下主要结论:
1)验证了MPS方法对船舶破舱进水数值模拟的适用性,研究表明,对于不同类型的船体截面模型,可以很好地预测船体截面的瞬时进水和相关运动响应。
2)受损孔的位置影响了破舱进水的进水量。开孔距静水面以下越远,进水量越大。
3)受损孔的位置也会影响模型的运动。开孔距水面以下越远,横荡运动和垂荡运动就越大,同时进水量也越大,进水速率更快。开孔是否全部浸没在水面以下对于横摇的方向有很大影响,同时浸没的深度会影响横摇的角度大小。
4)内部挡板显著影响了模型的运动。垂直挡板比水平挡板对破舱进水的运动响应影响更大,尤其是横摇运动。这主要是由于垂直挡板对入射流扩散的影响较大,导致舱内流体分布不均,间接增加了横摇力矩。
本文的研究有助于了解不同位置的受损孔和挡板位置类型对船舶破舱进水过程中瞬时进水阶段船舶运动特性的影响,为三维模拟的进行奠定基础,对舱内的舱室布置有一定的指导意义。
