黏土中桩靴底部吸附力产生机理研究

2022-10-18闫国斌尹蒋松李婷婷

海洋工程 2022年5期

闫国斌，潘池，李飒，尹蒋松，李婷婷

(天津大学建筑工程学院岩土所，天津 300350)

近年来，随着海洋资源的开发利用，移动自升式钻井平台在油气开采和海上风电安装中得到了广泛应用。当其作业结束拔桩时，黏性土地基对桩靴底部产生的吸附力会导致拔桩困难，该问题目前仍被海洋岩土工程界的众多学者所关注[1]。据相关报道在一些特殊情况下平台拔桩的时长可达数十周[2]，这对工程正常运转造成了极大的影响。

为此国内外众多学者相继针对结构物上拔时其底部所受吸附力的产生机理展开深入研究。Vesic[3]对埋入黏土中的圆形锚板进行上拔试验，研究了锚板上拔过程中孔隙水压力变化情况，并定义其上下超静孔隙水压力差值为锚板所受吸附力；Byrne和Finn[4]对黏土中裙式载荷板进行了拉拔试验，认为板土之间的黏聚力是吸附力的主要组成部分，并提出采用反向地基承载力理论来求解吸附力的上限值；Craig和Chua[5]通过离心机模型试验探究得出桩靴上拔时底部土体先前所受压载及桩靴贯入速率都对桩底吸附力的产生有着重要影响；Sawicki和Mierczynski[6]通过室内模型试验，从荷载板周围所受应力变化的角度出发，指出板与底质之间的吸附力是荷载板上拔困难的重要因素；Purwana等[7]通过离心机模型试验研究了正常固结软黏土中，从桩靴工作时长及工作荷载等因素角度对桩靴底部吸力产生机理进行分析；Lehane等[8]通过土工离心机模型试验研究了黏土中拔桩速率对基础各部分受力的影响情况，认为结合基础宽度和固结系数的归一化速率是预测吸附力的一个有效指标；Bienen等[9]，Gao等[10]对底部带有喷冲装置的桩靴进行土工离心机试验，分析了喷冲率及上拔荷载大小对桩靴吸附力的影响；Kohan等[11]研究了软黏土中桩靴埋深比对拔桩时底部吸附力的影响，得出吸附力与埋深比正相关；Hossain等[12]利用离心机试验与有限元模拟分析不同形状桩靴在贯入与上拔时受力变化情况，研究表明带开口桩靴与常规桩靴相比，吸附力有所减小。以上学者主要从上拔速率和埋深比这两个因素来探究桩靴吸附力的变化情况。

国内学者诸如冯国栋等[13]通过室内试验研究吸附力本质及其影响因素，研究指出物体所受吸附力与边界条件和物体刚度有关；金广泉等[14]对圆底形和方底形物体展开室内拉拔试验，认为物体所受吸附力与其底部土质的均匀性存在关系；韩丽华等[15]对沉箱吸附力进行模拟试验，并指出单位面积吸附力与结构物底部大小无关；张爱霞等[16]通过室内试验及数值模拟研究了底质固结效应对平台拔桩吸附力的影响，并得出吸附力与桩靴上拔力之间的比例关系。以上学者从桩靴形状及底部土体特性等方面来研究对吸附力的影响。

由此可见，拔桩时底部吸附力涉及诸多影响因素，且由于不同工况下桩土相互作用机理复杂，因此国内外学者基于各自研究持有不同的说法，且目前尚未形成行业内一致认可的观点，因此，探究拔桩过程中的桩靴底部吸附力特性有着非常重要的意义。

国内外学者诸如于徽和王闻恺[17]，Han等[18]，Hossain和Dong[19]，Purwana等[7]均通过粒子图像测速技术研究发现黏土中桩靴上拔初期在桩靴底部会形成一个不断变化的空腔，这是由于黏土具有一定的结构强度，因此当桩靴向上移动时，其周边土体无法立即将其下部空腔填充密实。由于插桩时外部竖向荷载较大，桩靴底部土体压密效果明显，且黏土的渗透性较差，因此桩靴在上拔过程初期，桩靴底面与其周边的黏土体近似形成了一个密闭的真空状态，在上拔力的作用下该空腔内外表面将逐步产生压力差，压力差使得桩靴底部出现真空吸力，从而阻碍桩靴上拔。

为此，基于饱和黏土中桩靴上拔室内模型试验，使用压力传感器、位移传感器、孔隙水压力传感器和单晶硅压力变送器来测量模型桩靴在上拔过程中的上拔力、负孔压和桩靴底部真空度的变化情况，探讨在不同形式的桩靴、不同拉拔速率及不同埋置深度条件下桩靴底部真空度的变化对桩靴底部吸附力的影响，以及吸附力与上拔力之间的变化趋势关系，并结合“真空吸盘效应”原理[20]，提出以桩靴底部真空度来计算桩靴底部所受吸附力的方法，为海洋钻井平台的拔桩工程实践提供一定的参考。

1 现有桩靴上拔力计算公式

关于自升式钻井平台的桩靴大都入泥一定深度，对桩靴上拔受力情况进行分析时，通常忽略横向受力而只考虑桩土竖向作用力，此时桩靴受到拔桩力，桩靴自重及其上部覆土重力Wa，桩靴及上部土体的侧剪切阻力Fs和桩靴底部的吸附力Fv这三大部分。因此，一般认为桩靴上拔力通常可表示为[21]：

Fb=Wa+Fs+Fv

(1)

其中，桩靴自重及其上部土重力Wa可按照式(2)计算：

Wa=Wb+Wc

(2)

式中：Wb为桩靴自重；Wc为桩靴上部圆台土体自重，见图1，其中倾斜角β通常取为土体的内摩擦角φ[22]。

图1 黏土桩靴上拔示意

桩靴及上部土体的侧剪切阻力Fs通常采用式(3)进行计算：

Fs=Su,avgHPs

(3)

式中：Su,avg为桩靴埋深范围内土体的平均抗剪强度；H为基础侧边高度；Ps为基础最大横截面长度。

目前国内外对于桩靴所受吸附力Fv的计算并未形成统一的结论，且存在众多分别适用于特定条件下相应的经验方法，大多是考虑基础材料、形状及埋深比等因素，根据试验结果进行修正而得到。

其中,Lee[23]通过对某海湾拉拔试验数据进行分析，发现数据点较大比例落在指数方程±50%包络线内，并基于此提出吸附力可表示为：

(4)

式中：Fq为桩靴底面土质承载力；B为基础宽度；D为基础埋置深度。

金广泉等[14]利用反向地基承载力理论，假设基础与周边土体达到极限平衡状态来求解结构物所受吸附力：

(5)

式中：A为桩靴底面水平投影面积；D为基础埋置深度；B为基础宽度；L为基础长度。

Das等[24]通过室内模型试验研究了饱和软高岭土中板锚底部吸力随埋深比的变化特性，并根据试验结果提出了吸力经验计算公式：

(6)

以上吸附力公式皆是基于不同条件下的试验研究得到的经验公式，对于具体工程实践仅供参考，因此在面对不同工况时仍需要选择合理可行的方法来进行预测分析。为了提高上拔力的计算精度，本文通过模型试验对饱和软黏土中桩靴底部吸附力的影响因素以及产生机理进行了研究。

2 室内模型试验

2.1 试验装置

试验选用一个尺寸为1 m×1 m×1 m(长×宽×高)的正方体渡漆钢模型箱，位于试验槽上方中心的反力架最大受荷20 kN。试验装置如图2所示。动力由三相电机提供，通过电气控制柜可实现桩靴的匀速贯入与上拔，整个加载系统传感器安装到位之后，连接DH5922N型号数采仪通过电脑采集数据并保存。电机下方安装LTR-10 kN型号拉压力传感器采集插拔桩阻力，反力架上焊接拉线式5G203-750型号位移传感器记录插拔桩位移，桩靴底部安装CYG41000KY型号孔压计测量插拔桩过程中桩靴底部的孔隙水压力，采用ZDY9800D0WY型号单晶硅压力变送器连接桩靴底部的气动软管，通过检测软管中的绝压变化来检测桩靴底部的真空度变化。

图2 试验槽实物及布置示意

模型箱内土样深度65 cm。根据工程中常用的直径18 m桩靴进行了缩尺(1∶100)，桩靴直径D=18 cm，高度H=7.2 cm。孔压计尺寸d×h=12 mm×13 mm，在桩靴底部斜面中心打孔略大于孔压计尺寸，加工卡槽便于安装孔压计以及走线。桩靴底部中心通眼直径5 mm，从桩腿侧边引出，并于孔中放置直径为5 mm的气动软管，软管的末端用来连接单晶硅压力变送器。本试验所用桩靴的模型简图如图3所示。

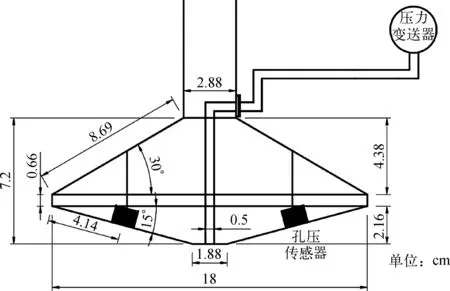
图3 试验所用模型桩靴尺寸

为研究桩靴上拔时其底部真空度峰值对吸附力的影响，本试验分别对桩靴做包裹单位面积质量为0.2 kg/m2的涤纶短纤针刺土工织布，底部斜面中心位置对称开直径25 mm孔洞(采用土工织布封住孔口)，以及开孔后连接通气胶管这三种不同形式的处理去调整桩靴与底部土体的边界接触条件，上述处理措施均在不同程度上改变了桩土之间的气密性。其中，在开孔桩靴贯入时，为避免土体进入胶管而堵塞，在桩靴底部孔眼上铺设单位面积质量为0.2 kg/m2的涤纶短纤针刺土工织布，并盖上密实的钢丝网进行加固增加强度，在其四周用环氧树脂固定。以上所述模型桩靴实物如图4所示，通过对不同形式的桩靴进行试验对比，分别探究桩靴底部真空度对桩靴底部吸附力的影响情况。

图4 试验所用模型桩靴

2.2 土体制备

试验所用土体为高岭土，试验前参照《土工试验方法标准》(GB/T 50123—2019)[25]对土体塑限ωP、液限ωL、相对密度GS、含水率ω与饱和容重γsat等基本物理指标进行测量，最终所得土体的具体指标参数见表1。

表1 土体物理性质指标

其中，用烘干法测量土体的含水率ω，用环刀法测量土体的容重γsat，试验土体的塑限ωP和液限ωL用液塑限联合测定仪进行三组平行试验，取其平均值作为液限值和塑限值。

土体制作时，将高岭土倒入搅拌桶中，按照水土质量比1.2∶1的比例混合，初始含水率约为液限的1.5倍，用搅拌机将水土搅拌均匀后分层填入试验槽内，再于土体表面铺设土工织布，上表面布置砂垫层以及排水管，然后表面覆盖多层塑料薄膜，引出水管，四周用黏土进行密封，并采用抽真空方法和堆载预压相结合来加速土体的固结。静置一个月左右，此时土体沉降约达土体原厚度的20%。

试验土体的不排水抗剪强度Su通过SZB-1.0型十字板剪切仪进行原位剪切试验测量得到。在土体试样深度为0.5D～2.0D范围内选取4个不同位置进行测量，并将测量所得结果进行直线拟合，测量所得不排水抗剪强度Su随深度Z变化曲线如图5所示。

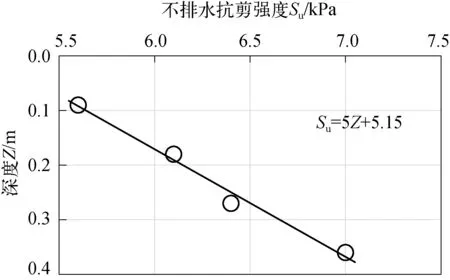
图5 利用十字板剪切仪测量所得不排水抗剪强度变化曲线

2.3 试验步骤

试验准备工作及重点操作步骤为：首先要检查试验槽密封性；试验抽真空采用双面排水，在槽底铺设5 cm厚砂垫层，其上放置绑扎土工织布的排水管，再加砂至垫层高度约15 cm，并盖上一层土工织布将土与垫层隔开。将高岭土置入搅拌桶内，按照水土质量比1.2∶1混合，初始含水率约为1.5倍液限，用搅拌机搅拌均匀，然后分层填入试验槽。土体表面铺设土工织布、砂垫层及排水管，并在垫层表面覆盖多层塑料薄膜，引出水管，四周使用黏土密封。采用真空预压与堆载预压结合的方法加速得到相应强度要求的试验土体。

制土完成后, 将土体表面刮平并加入2 cm高水层以防止空气进入。通过电气控制柜设置桩靴贯入与上拔速率，同时利用数采仪进行试验数据的采集。利用十字板测量模型槽中试验土体的不排水抗剪强度Su。待试验用土恢复后，换取不同的位置对不同形式的桩靴重复上述步骤并记录相关数据。其中，在桩靴贯入过程中会产生超孔压，当桩靴以1 mm/s的速率贯入指定深度后停止加载，此时静置一段时间，待超孔压全部消散之后，再以相应速率上拔，至桩靴上升至土体表面关闭数采仪停止采集数据。

研究具体试验方案如表2所示。

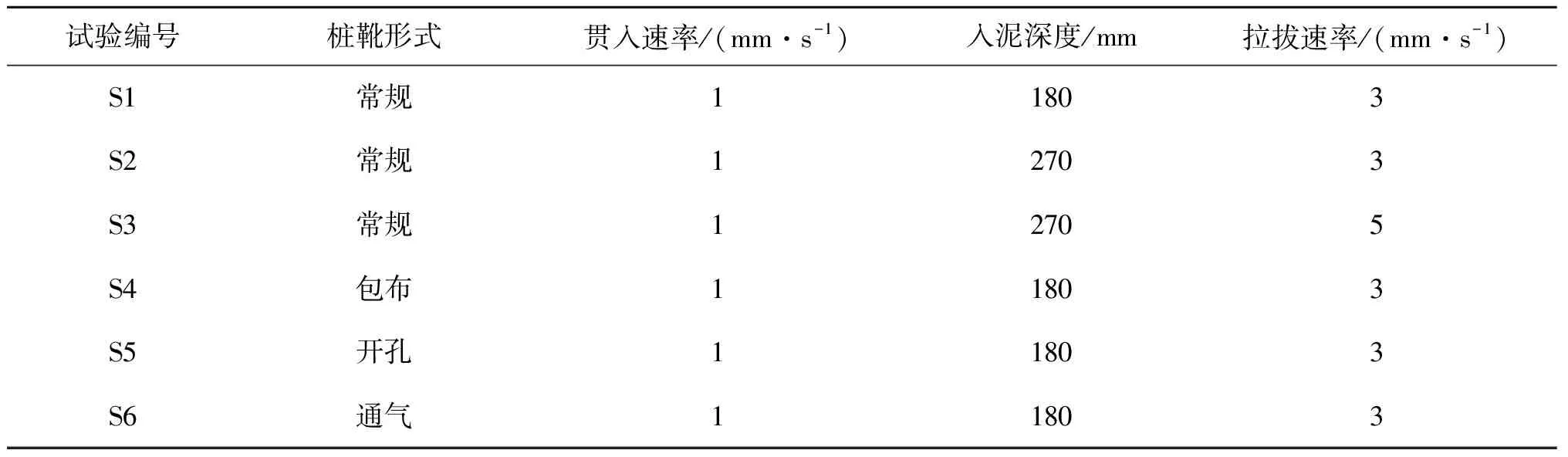
表2 试验方案

3 试验结果及分析

在研究中，分别测量了孔隙水压力和真空度。孔隙水压力是孔隙液体的测压管压力，实际上是一种相对压力(相对于预先认为0压力的大气压力)，有正压和负压之分[20]。真空，是指在给定空间内低于一个标准大气压强的气体状态，是描述气体状态的一个定义，为描述该空间气体的稀薄程度，用“真空度”这个指标进行衡量。

当真空度向周边土体扩散与传递时，可引起周边土体孔隙水压力的变化，从而产生负孔压。真空度可以看做是负压产生的一个必要条件。为了对吸附力产生机理进行探讨，文中对孔隙水压力和真空度分别进行了探讨。

试验结果如表3所示。图6为试验S1,S4,S5,S6所得不同形式的桩靴底部真空度与负孔压随拔桩位移变化趋势，由图可以看出，在拔桩位移小于50 mm的初始阶段，真空度与负孔压值均呈快速增大趋势，但在试验中由真空表测得的真空度值与孔压计探头测得的负孔压值并未同时达到峰值，且两者达到峰值的位移距离小于0.1D，真空度存在滞后现象。这是由于真空度需要通过气动软管反映到真空表处，因此存在一定的延迟效应。

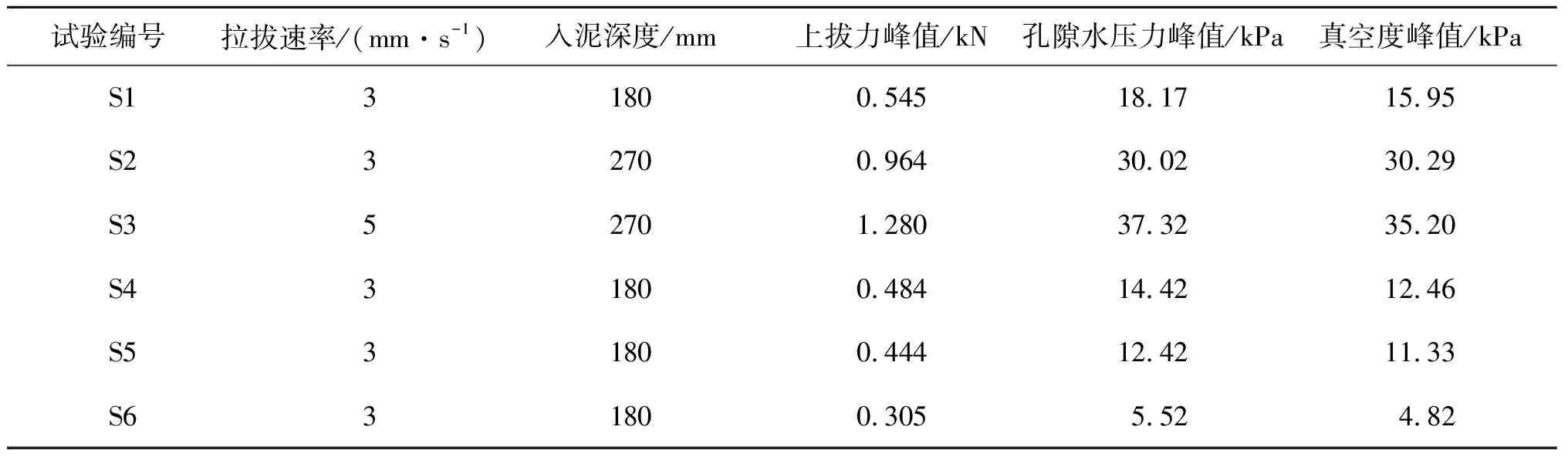
表3 试验结果

当真空度与负孔压值达到峰值后，两者均处于减小阶段，但减小的速度显著小于初期上升时的速度，这是因为随着桩靴持续上拔，其底部周边土体发生持续变形，真空状态遭受破坏，真空度逐步减小，桩靴底部空腔内外气压逐步达到平衡，负的超静孔隙水压力随之消散为0，但由图6可知在负的超静孔隙水压力为0后真空度值并未降至0，这是由桩靴底部黏着有部分黏土层造成的。

图6 真空度与负孔压测试结果对比

张功新等[25]基于伯努利方程和平衡方程推导了在某点真空表反映的真空度值与孔压计反映的孔隙水压力差值的理论关系式，可表示为：

(7)

式中：Pa为真空度值；Pw为孔压值，此处取负孔压的绝对值；γw为水的重度；L0为地下水位距离真空表的长度；P0为一个标准大气压值。

图7为根据式(7)由试验所测孔压值换算为相应真空度值与试验中真空表所测真空度值随拔桩位移变化的对比曲线。需要说明的是，由于真空度相对于负孔压存在滞后，图7的计算值为真空度向左平移0.1D后的计算值。由图7可知，换算值与实测值在上拔的初始阶段与峰值后的下降阶段均呈现出较高的一致性，且在接近峰值附近时，两者平均误差仅为1.37%。随着桩靴位移的增加，由于桩靴底部有附着的黏土，因此真空度测试值存在一定的误差，但由于文中主要研究拔桩真空度峰值附近的变化情况，因此在真空度值降低阶段的数值对论证结果影响不大。

图7 常规桩靴上拔时真空度试验值与负孔压换算值对比

对桩靴进行包布、底部开孔、底部通气等不同条件的处理后，试验测得的真空度如图8所示。由图8可知，拔桩位移为1D时，在不同条件的桩靴上拔过程中，试验所得桩靴底部真空度值均在不断变化，反映出桩靴底部真空区域是一个动态变化的过程。不同条件下拔桩时底部真空度峰值均在1/3D以内产生，之后随着底部空腔密封遭受不同程度的破坏，真空度值呈现明显下降趋势。此外，真空度峰值大小为常规>包布>开孔>通气，这是由于常规条件下，桩靴外部荷载作用下与黏土底质结合较为紧密，因此拔桩时其底部空腔密封性最好；当对桩靴做包布处理时，土工织布减小了桩靴与黏土底质之间的黏合，因此拔桩时底部空腔密封性次之；当对桩靴底部斜面中心位置对称开孔并采用土工织布封住孔口处理时，等同于改变了桩土接触边界的密封性，因此拔桩时，底部空腔密封性与包土工织布时相差不大，均小于常规条件下桩靴底部空腔的真空度；当对桩靴底部对称开孔后连接通气胶管处理时，尽管通气胶管截面面积仅占桩靴底面面积的7%，但由于其直接改变了桩靴底部空腔内外的压力差，显著地影响了空腔内外的气压平衡，因此由试验可知，拔桩时桩靴底部真空度值在不到6 kPa时便停止增加，且在之后的整个位移过程中处于稳定状态，这说明此时桩靴底部内外气压基本保持平衡。

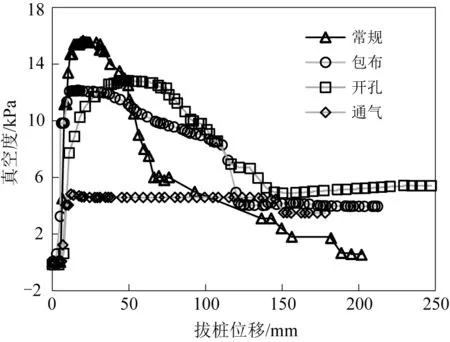
图8 不同条件桩靴底部真空度随拔桩位移变化

拔桩时桩靴贯入深度对桩靴底部真空度值的影响见图9。图9为常规桩靴在不同贯入深度下桩靴底部真空度值随拔桩位移的变化趋势，据图可知，桩靴贯入深度增大，则真空度峰值显著增大，且贯入深度1.5D时真空度峰值约为贯入深度1.0D时真空度峰值的2倍。

图9 贯入深度对常规桩靴底部真空度的影响

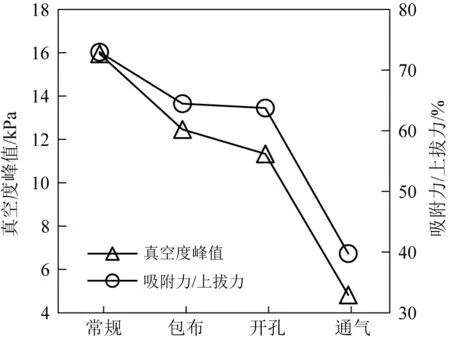
图10 不同条件桩靴吸附力占比及真空度峰值变化对比

4 基于真空吸盘理论的桩靴吸附力计算

真空吸盘通常是利用真空吸力来抓取物品的一种自动化工具，由于其便捷性、无污染而在自动化生产线上被广泛用来运输物品等。其按照真空产生方式可分为主动型真空吸盘与被动型真空吸盘[26]；按照吸附模式可分为柔—刚贴合式，以及刚—柔贴合式(即为刚性的真空吸盘来抓取柔性的应用对象[27])。

黏土中桩靴上拔初期存在相似于被动型刚—柔贴合式真空吸盘原理的情况。真空吸力产生的全周期过程可分为3个阶段：插桩过程可认为是压力施加阶段，拔桩初期可认为是吸力产生阶段，最后为桩底土脱离阶段，其示意如图11所示。

图11 真空吸盘原理

将桩靴底部吸附力视为真空吸力, 则吸附力可由式(8)表示：

Fv=P0n1dAe-Pan2dAi

(8)

式中：P0为大气压强，一般取101.325 kPa，Pa为绝对压强，n1和n2分别为由内向外和由外向内的垂直朝向桩靴底部真空区域的单位法向量，dAe和dAi分别是真空区域外部和内部无穷小面积[26]。

根据上述原理, 鉴于桩靴底部真空区域内部面积Ai与真空区域外部面积Ae上法向量的对应性，`为简化计算，假设Ai=Ae，则桩靴底部的单位吸附力可用ΔP来表示，即：

ΔP=P0-Pa

(9)

在试验中Pa通过压力变送器后端连接的气动软管近似反映绝对压强的变化。

根据式(7)和式(9)，在已知孔压的条件下，可以得到上拔过程中吸附力的大小。采用上述方法，得到试验以及根据Kohan等[11]、韩丽华等[15]、Li等[28]试验测得的孔压数据计算得到的相应单位吸附力，将计算结果与各个试验推荐的吸附力数值进行比较，结果见图12。其中约73%的数据位于30%误差线内。