近壁面柔性圆柱流致振动—拍击耦合特性试验研究

朱红钧，赵宏磊，谢宜蒲，张 旭

(西南石油大学 石油与天然气工程学院，四川 成都 610500)

海底管道作为油气资源输送的“生命线”，因海床地形起伏及局部冲刷作用易形成悬跨段，在洋流作用下会发生涡激振动响应，存在疲劳失效的风险。20世纪以来，大量学者采用试验和数值模拟的方法对涡激振动现象进行了研究，但主要针对的是无壁面边界影响的自由振动刚性柱体，关于大长径比柔性悬跨管的涡激振动研究十分有限，由此引发的管床碰撞与流致振动耦合方面的研究尚属空白。

Bearman和Zdravkovich[1]、Grass等[2]、Buresti和Lanciotti[3]、Lei等[4]试验发现流体绕过近壁圆柱时，壁面的存在对周期性脱落的旋涡及柱体上的流体作用力有很大影响，指出下侧旋涡被完全抑制的临界间隙比约为0.2～0.3。然而，Wang等[5]研究发现即使间隙比很小时，没有周期性对称泄放尾涡的柱体依然可以发生振动。Tham等[6]、Li等[7]、Chern等[8]、Chen等[9]、Gao等[10]和花阳[11]开展了低雷诺数条件的数值模拟研究，发现近壁柱体振动时下侧旋涡被部分或者完全抑制，非对称或单排脱落的旋涡使其振动响应与无壁面影响的圆柱差异较大。近10年，部分学者发现小间隙比柱体涡激振动时会与壁面发生碰撞。Zhao和Cheng[12]模拟发现壁面反弹系数对柱体振幅和尾涡脱落模式的影响不可忽略。Chung[13]模拟了低雷诺数Re=100时柱体的单自由度振动，指出碰撞并没有导致振幅与频率的显著变化。Barbosa等[14]通过试验研究发现柱体与壁面发生碰撞的临界间隙比为0.75，且振动呈现非对称性。郭飞[15]利用大涡模拟方法捕捉了0.25≤G/D≤0.50时圆柱与底壁的碰撞现象，指出碰撞造成圆柱后方边界层生成一个分离涡。Daneshvar和Morton[16]在较宽的约化速度范围内观察到了连续碰撞现象，拓展了振幅的碰撞分支。

上述研究主要针对近壁刚性柱体的涡激振动及碰撞响应，实际海管悬跨段较长时表现出一定的柔性，Zhu等[17]初步探索了间隙比为0.2的柔性悬跨管管床拍击现象，分析了横向和流向振动与管床拍击间的交互影响，指出管床拍击时不仅横向运动速度恢复较慢，流向运动加速度也存在明显的波动。但不同间距的大长径比柔性管跨诱发高阶模态振动时的管床拍击机理尚未明晰，尤其是横向振幅的空间分布与管床拍击模式间的内在联系有待阐明。因此，基于高速摄像非介入测试方法开展了大长径比柔性悬跨管涡激振动及管床拍击试验，剖析了间隙比及约化速度对于振动—拍击的影响规律，并判别了管—床拍击模式。

1 试验布置

近底床柔性悬跨管涡激振动及管床拍击试验在水槽中开展，水槽试验段尺寸为2.0 m×0.5 m×1.0 m(长×宽×高)，两侧及底部均为透明玻璃以便高速摄像机捕捉管道振动与碰撞底床的过程。试验模型选用长0.52 m、外径6 mm的硅胶管，长径比约为87，杨氏模量为3.59 MPa。悬跨管壁厚1 mm，内部充满水，两端通过螺钉密封，充满水的管道质量与其排开水的质量之比为1.02，轴向预张力设为2.35 N，以保证初始布置后的柔性管无悬垂段。如图1所示，悬跨管平行水槽底壁并与来流的垂直方向呈30°夹角布置，两端用不锈钢垂直约束杆固定，通过约束杆的升降来调节管床初始间隙比的大小。悬跨管上游2 m处布置声学多普勒流速仪(ADV)以监测来流速度，通过调节循环水泵频率，开展约化速度(Ur=U/fnD)及雷诺数范围分别为3.44≤Ur≤14.43和650≤Re≤2 780条件的试验测试。由悬跨管在静水中的振动衰减试验测得前三阶固有频率分别为：f1=5.34 Hz、f2=11.00 Hz、f3=17.09 Hz，系统的阻尼比为0.072。

图1 试验布置

2 图像后处理

为了同步捕捉柔性悬跨管横向和流向的振动位移，在水槽一侧和下方共架设两台同步触发的高速摄像机，布置位置如图1所示。高速摄像机的采集频率为100 Hz，每个试验组次采样时间为50 s。为给高速摄像机提供可辨识的标记点和满足捕捉悬跨管振动空间分布特征所需的采集分辨率，沿模型管道轴向均布26个黑色标记点，标记点宽4 mm，两个标记点间距为16 mm，以悬跨管远离镜头的一端为原点建立轴向坐标系s，以得到每个标记点的初始位置坐标。图2描述了图像后处理流程，以静水状态下拍摄的初始图像标记点为模板，在每帧图像中将各标记点所占像素单元与实际尺寸关联，并设置搜索域，在搜索域内利用图像矩不变量值匹配识别各标记点，再得到标记点的振动位移。通过时序图像的批处理，得到26个标记点的振动位移时间序列。

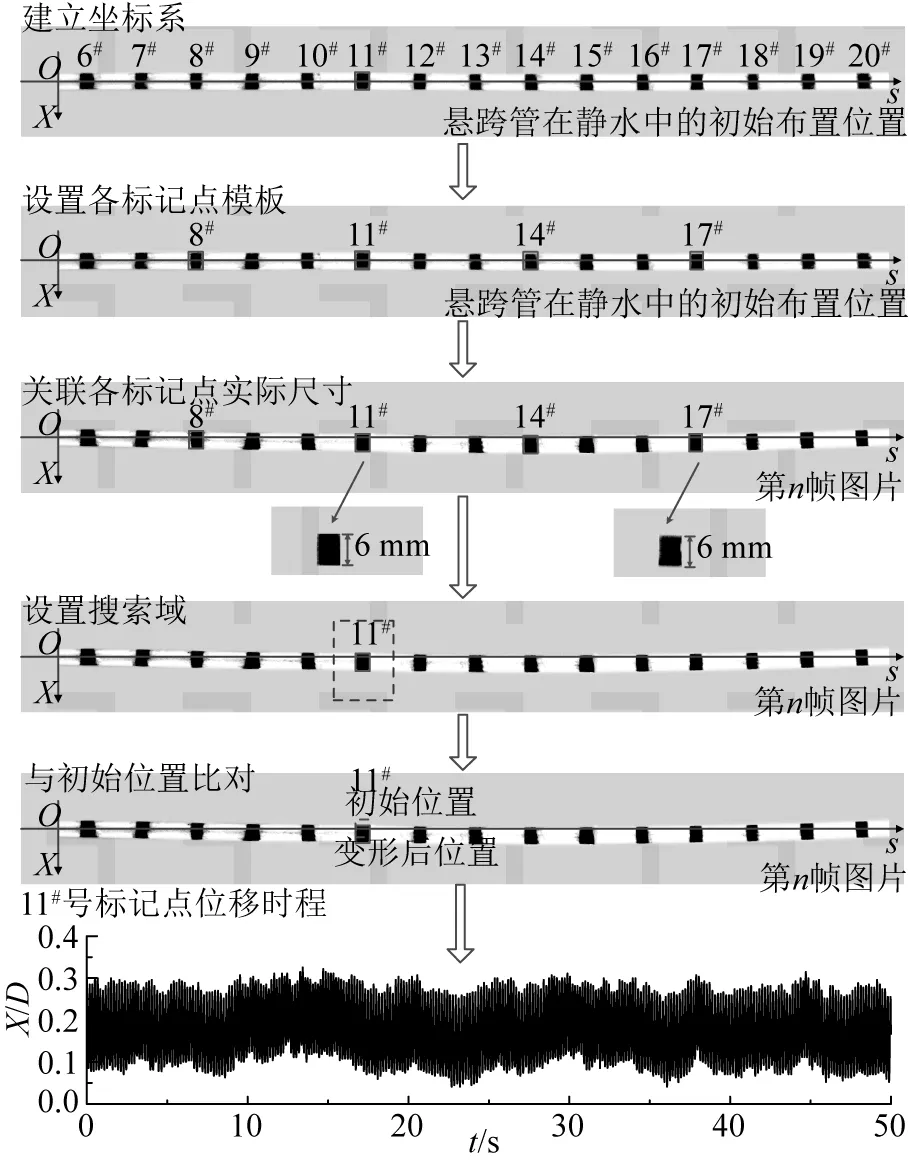
图2 图像后处理方法

3 间隙比及约化速度对悬跨管涡激振动响应的影响

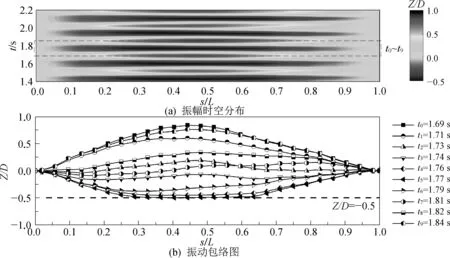
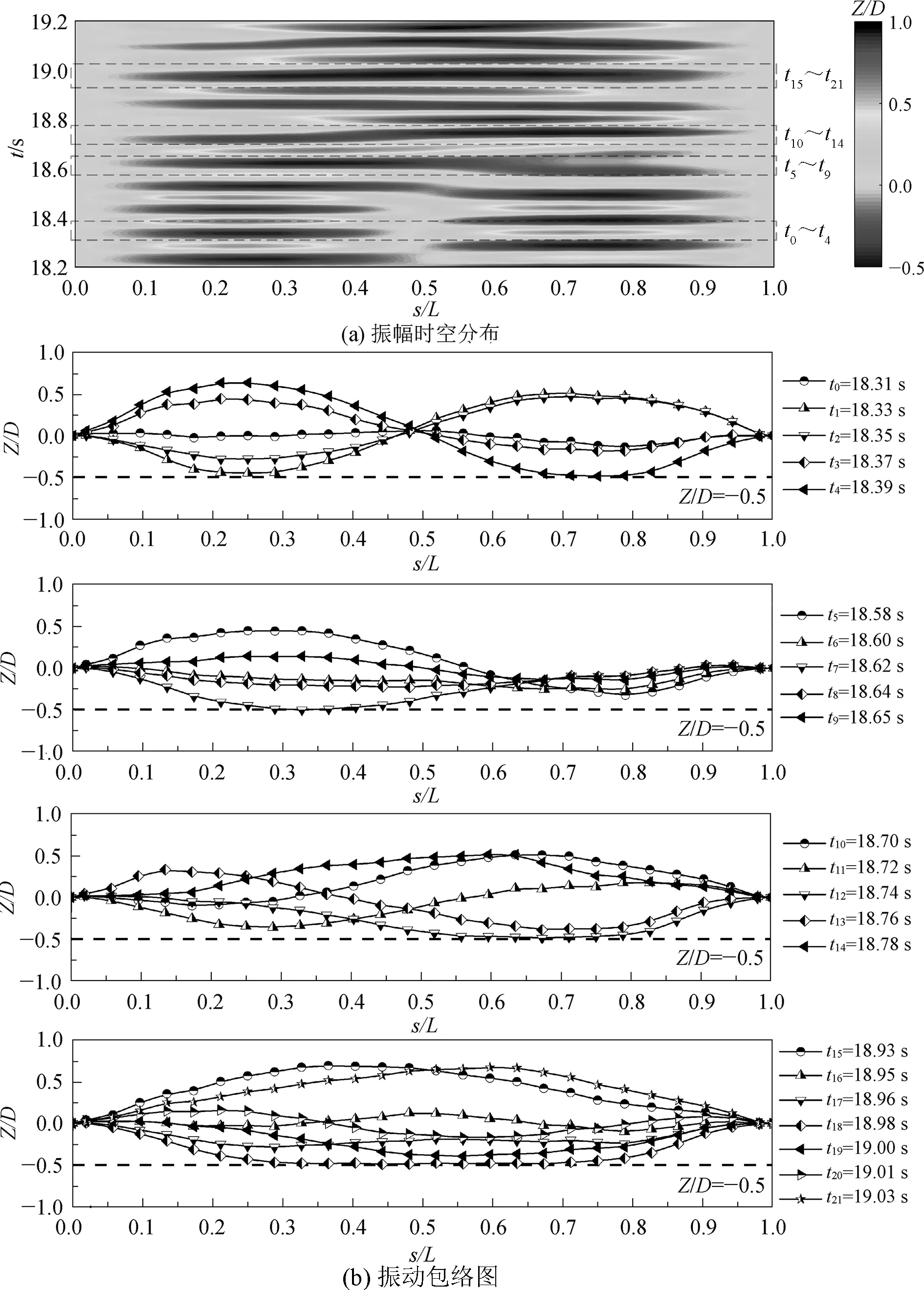
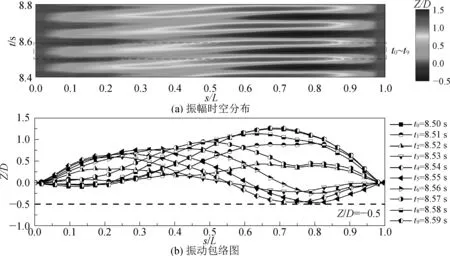
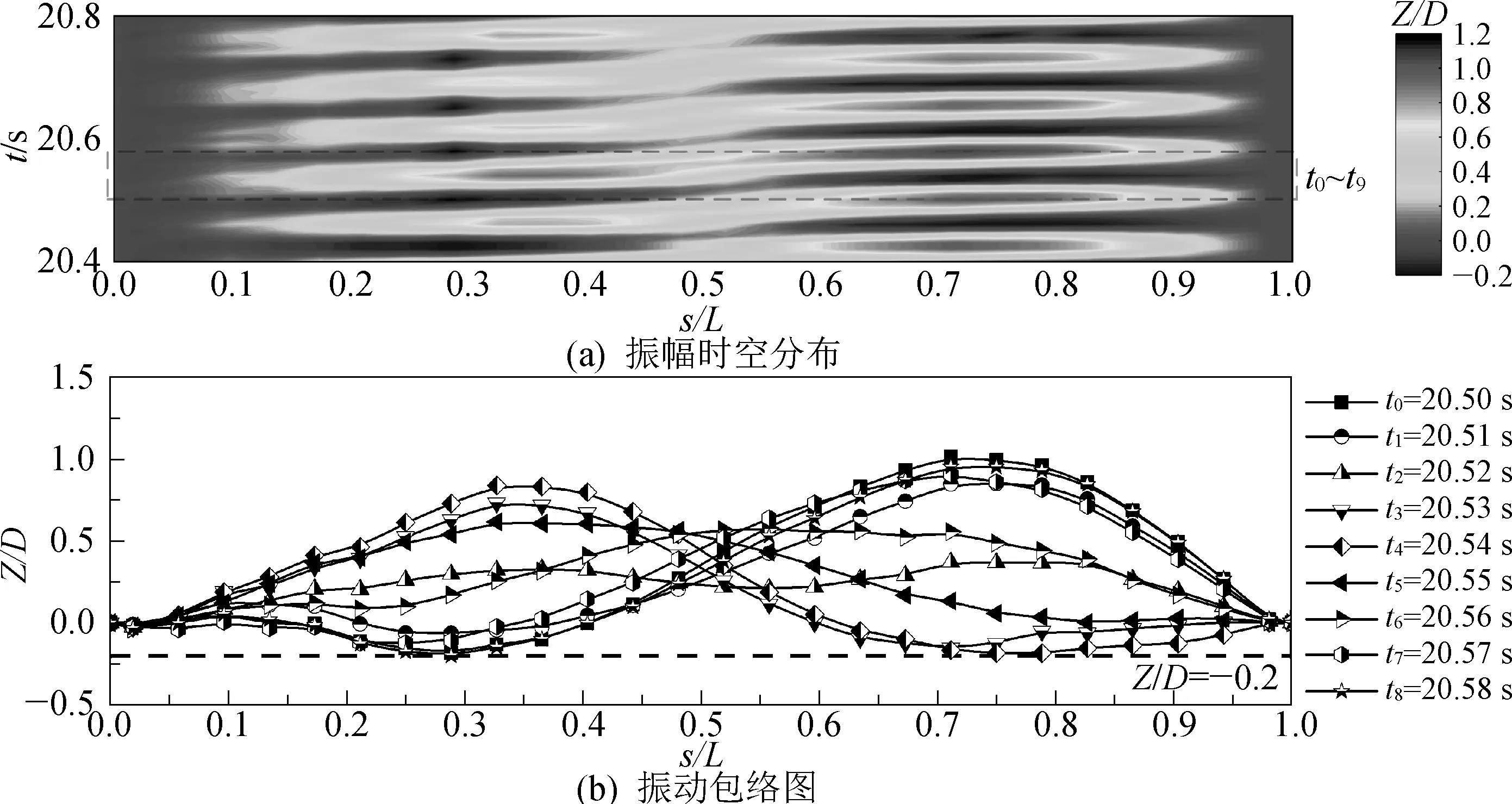
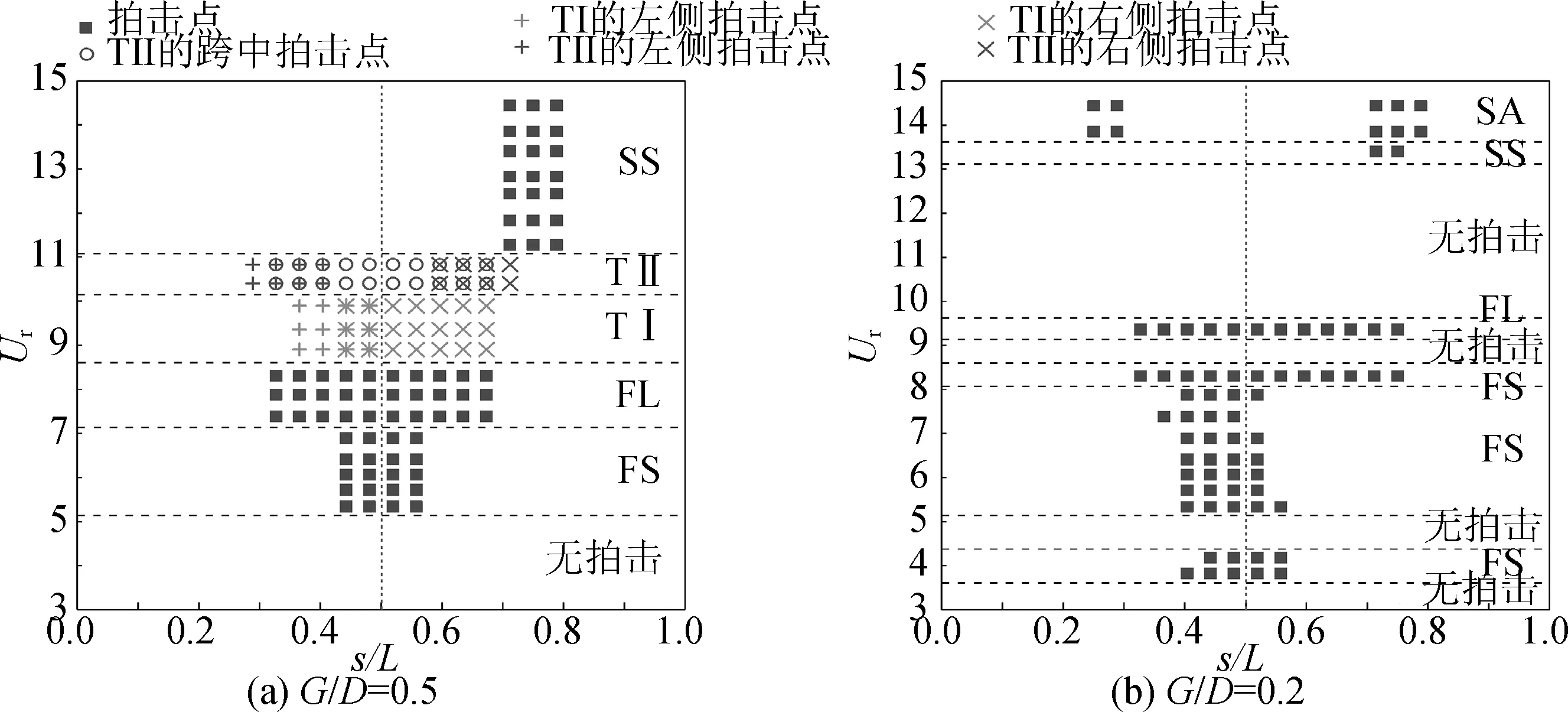
图3对比了无底壁影响(G/D=49.5)及G/D=0.8、G/D=0.5和G/D=0.2时柔性悬跨管横向振幅的空间分布以及典型标记点处的主振频率fz/f1和模态权重w的变化，其纵坐标为来流的约化速度。从振幅空间分布可以看出，随着约化速度的增加，悬跨管被激发的主导振动模态由一阶逐渐过渡到二阶。对于无底壁影响的悬跨管，在Ur=3.40～5.34范围内，二阶模态贡献度极小，振动由一阶模态主导，均方根振幅只在跨中附近存在最大值，且随约化速度的增加而增大，主振频率逐渐增至一阶固有频率附近，在Ur=5.34时出现频率锁定。当5.34

图3 不同间隙比下悬跨管横向振幅空间分布及典型标记点的主振频率与模态权重

同样，当柔性管靠近底壁时，因攻角的存在，G/D=0.8、G/D=0.5和G/D=0.2时的柔性管空间振动关于跨中均呈现一定的不对称性，且间隙比越小，二阶模态主导振动的不对称性越明显，这与振幅的大小及模态转移有关。三种间距下，悬跨管振幅随约化速度增加的变化规律基本一致，最高振动主导模态均达到了二阶，但随间隙比的减小，一阶向二阶模态转移的临界约化速度越高，说明壁面的存在导致了模态转移出现滞后现象，且间隙比越小，滞后现象越严重。具体表现为G/D=0.8、G/D=0.5和G/D=0.2时振幅均未出现二阶振动的下分支，即主振频率尚未脱离二阶固有频率，在G/D=0.2时甚至未达到频率锁定区，仅在Ur=13.85和Ur=14.43表现出二阶振动特性，处于二阶响应的初始分支。三种间距的柔性管二阶模态权重超过一阶模态的临界约化速度分别为Ur=8.90、Ur=10.83和Ur=13.40。此外，随着间隙比的减小，柔性管的最大均方根振幅也不断减小，表明壁面的存在一定程度抑制了涡激振动响应。

4 典型工况悬跨管振动的空间分布

图4为G/D=0.5、Ur=7.38时悬跨管的振幅时空分布及振动包络图。此时悬跨管振动呈现明显的周期性，时空分布呈驻波形式，振幅只在跨中附近存在一个波峰，从跨中至两侧振幅逐渐减小，表现出典型的一阶主导振动响应。选取一个振动周期t=1.69～1.84 s绘制瞬时包络图，短划线(Z/D=-0.5)表示底床位置，对应悬跨管下行能达到的最大负向位移，而悬跨管正向最大位移明显大于初始间隙(0.5D)，即振动关于初始位置不对称，在背离底床一侧具有更大的振动位移。t=1.69～1.77 s时管道从距离壁面最远的位置向下运动，在t=1.77 s时跨中部位的管段与底壁发生碰撞，反弹后，运动改向，t=1.77～1.84 s悬跨管上行运动，一个振动周期内伴随一次管床拍击过程。

图4 G/D=0.5、Ur=7.38时振幅时空分布及振动包络图

图5展示了G/D=0.5、Ur=9.36时管道振幅时空分布及振动包络图。

图5 G/D=0.5、Ur=9.36时振幅时空分布及振动包络图

此时振动从一阶模态向二阶模态过渡，从行波图中可以看出振幅波峰位置不再固定于跨中位置，而是随时间变化在管道轴向发生转移。从瞬时包络图中可以看出，第一个振动周期行波从右侧向左侧传递，管道并未与底床发生碰撞，在第二个振动周期中，行波从左侧传递到右侧，在t=4.18～4.19 s时发生管床拍击。故两个振动周期发生一次管床拍击，即拍击周期是振动周期的2倍，且拍击过程中碰撞位置随时间发生改变，表现为左侧管段先触底，右侧管段后触底。

图6为G/D=0.5、Ur=10.83时柔性悬跨管的振幅时空分布及振动包络图。此时振动仍处于从一阶模态向二阶模态过渡阶段，主导模态在一阶和二阶模态间来回切换。t=18.31～18.39时，振动包络图在悬跨管跨中存在单一节点，呈现标准的二阶振动，s/L=1/4和3/4部位发生交替拍击；t=18.58～18.78 s时，悬跨管拍床位置从左侧转移到右侧；在t=18.93～19.03 s时，悬跨管主导振动模态变为一阶，拍击位置迁至跨中，发生拍击的跨长增长。

图6 G/D=0.5、Ur=10.83时振幅时空分布及振动包络图

图7描述了G/D=0.5、Ur=13.85时管道的振幅时空分布及振动包络图。此时，振动由二阶模态主导，但右侧管段振幅峰值大于左侧，沿管轴方向振幅不对称，一个振动周期内只有右侧管段发生一次拍击，振动周期等于拍床周期。与之不同的是，G/D=0.2、Ur=14.43时悬跨管左右两侧管段发生周期性交替拍击，拍击周期是振动周期的2倍，其振幅时空分布及振动包络图如图8所示。

图7 G/D=0.5、Ur=13.85时振幅时空分布及振动包络图

图8 G/D=0.2、Ur=14.43时振幅时空分布及振动包络图

5 管—床拍击模式

根据悬跨管的主导振动模态与拍床特性，试验共发现了6种管床拍击模式如图9所示，分别为一阶模态主导的小段拍击(FS)、一阶模态主导的大段拍击(FL)、一阶向二阶模态过渡时的Ⅰ型拍击(TⅠ)、一阶向二阶模态过渡时的Ⅱ型拍击(TⅡ)、二阶模态主导的单段拍击(SS)和二阶模态主导的双段交替拍击(SA)，其中FS、FL、TⅠ、SS及SA型拍击均为周期性拍击，而TⅡ拍击为非周期性拍击。

图9 管—床拍击示意

以G/D=0.2、Ur=6.06为例，此时振动由一阶模态主导，当悬跨管下行至最低处时，跨中部位的4个标记点(11#～14#)与底壁发生拍击，而其余管段均未与底壁发生触碰，由于拍击长度相对较短，故将该拍击模式命名为一阶模态主导的小段拍击。随着约化速度的增加，悬跨管的振幅增大，但整体振动仍由一阶模态主导，当G/D=0.5、Ur=7.38时，参与管床拍击的标记点个数增加至10个，较之FS拍击段明显增长，故将此类型称为一阶模态主导的大段拍击。考虑模态过渡时的切换特性将G/D=0.5时Ur=9.36与Ur=10.83工况下的拍击模式分别命名为一阶向二阶模态过渡的Ⅰ型拍击模式(TⅠ)和Ⅱ型拍击模式(TⅡ)。当二阶模态主导时，为区分单侧管段拍击和两侧管段拍击，将G/D=0.5、Ur=13.85和G/D=0.2、Ur=14.43的拍击模式分别称作二阶模态主导的单段拍击(SS)和双段交替拍击(SA)。

不同拍击模式的管床触碰部位如图10所示，其横坐标为悬跨管轴向随体坐标，纵坐标为约化速度，TⅠ模式和TⅡ模式的拍击位置随时间发生变化，用符号“+、×、○”进行区分。与G/D=0.5相比，G/D=0.2时拍击随Ur的增加有不连续性，未拍击区内悬跨管的振幅小于振动平衡位置向上的偏移量与初始间隙之和。

图10 管床拍击位置的空间分布

6 结 语

基于高速摄像非介入测试方法，对不同间隙比的近底床柔性悬跨管涡激振动与管床拍击特性进行了试验研究，分析了间隙比及约化速度对振动—拍击耦合响应的影响规律，并辨识了6种管—床拍击模式，主要结论如下：

1)随管床间隙比的减小，一阶向二阶模态转移发生在更高的约化速度的情况，且振幅峰值及锁定区主振频率均有所减小，过渡过程中存在时间上的模态切换现象。

2)振动平衡位置向背离底床一侧偏移，致使管床拍击时的振幅需等于新平衡位置至底壁的间距。在此条件下，根据悬跨管振动的主导模态与拍击特性，辨识了6种管—床拍击模式，包括一阶模态主导的小段拍击、大段拍击，一阶向二阶模态过渡时的Ⅰ、Ⅱ型拍击，以及二阶模态主导的单段拍击、双段交替拍击，其中过渡拍击模式与振动模态的竞争及振幅的空间分布密切相关。